algebra-as-praxis - Tumblr blog

[algebra-as-praxis]

Factors, Terms, and Exponents

When you learn exponents in school, the language we tend to get taught about them is actually very unclear and can lead you to make mistakes and misunderstand the concept entirely. I intend to clean this up from the bottom floor.

I: Types of Math Problems

(we're gonna gloss over things like proofs and logic, this is just about algebra and arithmetic)

A math problem is more accurately called a statement. Statements can be expressions, equations, or inequalities. Both equations and inequalities are comparisons.

Any statement can either be true or false. Unless we are otherwise asked to figure out the factual nature of the statement, typically we just assume any statement given to us in math class is true.

An expression is any statement about how you'd like numbers to interact, but excluding the actual result of that interaction. For example, if I said I was going to buy two sandwiches at $4 each, we would understand the cost of that as being found with the expression 2 × 4.

Algebraically, if we have some unknown value but we know things we want to do with it, we can use an expression to show that interaction without bothering to find the unknown value yet. If I have x dollars in my pocket and I know every piece of candy I want to buy is 50 cents, I could write the expression x/0.5 to show the amount of candy I could buy; then, when I finally check my pocket to see how much money I have, I could solve it. And I could use that same problem any day, since I have the setup for the problem already.

An equation is a statement that sets two expressions equal in value to each other. An equation is most easily identified by the inclusion of an equal sign: =

Equations are split between its sides -- the expression on the left side of the equal sign, and the expression on the right side of the equal sign. So, in the equation 3x + 4 = 17 + 5x we can see the left side is 3x + 4 and the right side is 17 + 5x, and the equal sign is simply telling us that these two expressions have the same value.

An inequality is a statement that tells you that two expressions are not equal, and in which way they are not equal. Inequalities can tell you that one side is greater than the other, or simply that they aren't equal. They can also tell you that they may be equal but also one side might be greater.

You can use > to mean the left side is greater than the right side, or < to mean the left side is less than the right side. You can also use either of these with a line underneath to show that they are "greater than or equal to" or "less than or equal to," like so: ≤ ≥

And if you use any inequality sign and put a slash through it, or even the equal sign with a slash through it, you are negating that sign, meaning it will be the exact opposite of what it normally means: an equal sign with a slash through it (≠) means "not equal to," whereas a less than sign with a slash through it (≮) means "not less than" (which is equivalent to "greater than or equal to").

Interrupting for a moment: There's this thing called the Law of Trichotomy ("trichotomy" means "three distinct possibilities"), which states that in any comparison of two values, exactly one of three things is true: the first value may be equal to the second value (x = y), or it may be greater than that value (x > y), or it may be less than that value (x < y). This also accurately implies that these are the only three comparative states of values.

This can be confusing the first time you hear it since you know about "greater than or equal to," which sounds like it implies two at once. But remember, the "or" does not mean "both at once." It in fact means "only one of these is true, but they are both possible."

II: Values, Factors, Terms

Every expression has a value. All values are made of one or more terms. And all terms are made of two or more factors.

Once you've performed all of the operations in an expression, you are going to be left with a single number. That number is the expression's value. But notice to find the value we had to actually do all of those operations. The value, therefore, is the result of all of those operations on those numbers.

The expression is split up into smaller values, called terms, which are groups of multiplication and division. Terms add/subtract with other terms.

So, for example, if we have the expression 3 × 12 + 7, there are two terms: 3 × 12 is the first term, and 7 is the second term. Notice that the two terms are separated by a plus sign: +. This is because all terms add/subtract, so you can think of the plus sign as being the thing that separates a problem into its individual terms.

Terms can have subterms. For example, in the term 3(17 - 2), there is a parenthetical statement, 17 - 2, which contains two terms, 17 and -2. Because those two terms exist inside of a term, they are this term's subterms. Likewise, we can call the term that contains these two terms their superterm.

Because terms are groupings of multiplication and division, the numbers you are multiplying and dividing by are that term's factors. Factors multiply in the same way that terms add. So, in the expression 3 × 12 + 7, there are two terms, 3 × 12 and 7, and in the first term you have two factors, 3 and 12; likewise in the second term you have "two" factors, 1 and 7.

IIa: Terms of 0, and Factors of 1

There are what I call "null operations," that is, an operation using a number that has no effect on a problem's value. For addition and subtraction, it's 0. You can add or subtract 0, and it doesn't do anything. For multiplication and division, it's 1; if you multiply or divide by 1, nothing changes.

Because of this, every problem you've ever done technically has an infinite number of these "plus zero" and "times one" operations hiding everywhere (zero property of addition and one property of multiplication). We just don't usually write it cuz... they don't tend to do anything.

But in the example above, we have the term 7. But to describe that number as factors, we said 1 × 7. This is because factors always multiply. But if there's no number next to 7, then what would it be multiplying? It must be 1 × 7, then.

This will come up soon, and is actually very important.

III: Exponents

We use multiplication as a stand-in for repeated addition. 3 + 3 + 3 + 3 + 3 is annoying to write, so instead we notice that we wrote 3 five times, and thus we can say 5 × 3. ----- "Wait why'd you write it in this order?", you might ask of me. "Five times three" has a missing word. It is actually "Five times of three." It's telling me what I have five of. Yes, it is totally acceptable to write 3 × 5, you can multiply numbers within a term in any order (associative/commutative properties of multiplication) but the language itself would imply 5 × 3.

So, like we use multiplication to simplify repeated addition, we need a way to talk about repeated multiplication. That's where exponents come in. Instead of 7 × 7 × 7 × 7, we can write 7⁴, read "seven to the fourth power," which gets shortened to "seven to the fourth." The four, written in superscript (super- as in above, -script as in writing, so "writing above"), is the exponent; the number it is next to is called the base of that exponent. Exponents indicate how many times a particular factor (the base of the exponent) exists in a term.

Notice this definition is different from what you're taught in school. In school, the definition you're given is "multiplied by itself this many times." But that's not a good description, and in fact the language there doesn't even accurately describe what's going on (if you multiply something by itself x times, you have x+1 of that factor, which is not what is going on).

IIIa: Prime Factorization

What we might consider the best way to represent the factors that make up a term is called prime factorization, where we list the prime numbers we'd have to multiply together to get the value of a term. Obviously this doesn't work for every number, but any integer (whole number) or rational number (fraction, terminating decimal, or repeating decimal) can be expressed this way.

Let's try this with the number 144:

144 = (4 × 36) = (2 × 2) × (6 × 6) = 2 × 2 × (2 × 3) × (2 × 3)

Rearranging the factors so all the common factors are next to each other: 2 × 2 × 2 × 2 × 3 × 3. There are four 2's, and two 3's. Therefore, the prime factorization is 2⁴ × 3².

We're gonna continue this next time, going deeper into exponents.

[algebra-as-praxis]

First post!! I wanted to show you how deep a rabbit hole you can dig with a very simple concept like, "What does 'four' mean?"

I have a number line.

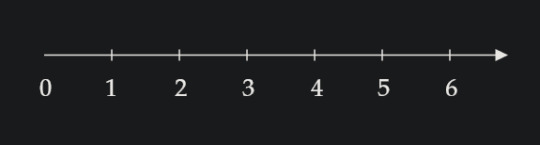
So, I'd like you to imagine that you've sat down across from me on your first day in class, and I put some kind of math worksheet with this number line on it that gives you a very simple-sounding task: "Circle four."

If you are like nearly every one of the older students I've had, you'll circle the number 4 on the line. And I'd say something like, "That is a perfectly reasonable response to this request. There is nothing wrong with what you've done. But aren't you suspicious about how simple this question sounds? Did you see that there was a twist coming?"

On a number line, the place where we've written 4 is not actually the value 4. It is more like the position 4; we would call this the ordinal number (a number used to track the positional order of things; another example of an ordinal number is the word "fourth," which tells you that there are three other things before that one).

So, if you just circled the number 4, you definitely circled the position, but the thing you circled isn't worth 4. If you were going to circle the thing that has the value (or cardinality, since we're counting individual objects) of 4, it would look something more like this:

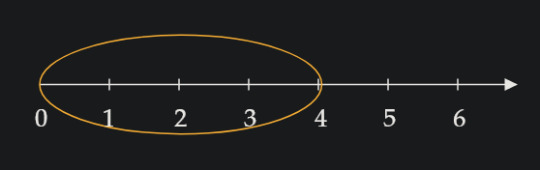
This is because in order to have the value of 4, you need everything that came before it! Imagine counting out candy while your kid sister steals and eats the candies you counted already. When you get to your final number, that number is not how many candies you have, but rather how many you counted cuz your sister's got 'em all! For the value of your candies to stay the same, you need all of them to be there!

"Four" could also look, less straightforwardly, like this:

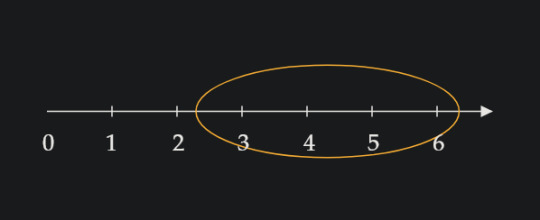
The distance from the start of the circle to the end is four; and since we're circling the line, the length of the line that is circled is four. If we imagine the circle starts (from the left) at the position of 2.3, it would have to end at the position (from the right) 6.3. If we find the difference of the numbers at these positions, we would be doing the equation 6.3 - 2.3 = 4.

A quick summary:

The position of a number is shown with an ordinal number.

The actual physical quantity of the individual items is shown with a cardinal number, which we more typically call the value.

We can find a value inside the ordinals by finding the distance between any two ordinals, via subtraction.

Okay... But notice we've used two words here that seem to imply the same thing: difference and distance. Let's clear this up real quick:

Difference is the result of subtraction. Generally, if we want to find the difference between two things, we subtract the first thing from the second thing:

second - first = difference

But that's not a rule, so much as a norm. In reality, if you wanted to find the difference of two numbers, the person asking had best be very clear which way they want you to do it, because if you reverse this you will get the negative of the result above!

For example, if you were asked to find the difference between 6 and 15, you would do 15 - 6 = 9. But if it's not clear and you instead did 6 - 15, you get -9.

If, however, someone wanted to know how far apart these two numbers are, they would not be asking the difference but rather the distance between these numbers. The result would therefore be the absolute value of either one of these subtractions:

|15 - 6| = |9| = 9, |6 - 15| = |-9| = 9 Same result!

This is in actuality the real use of absolute values. Absolute value is typically shown as "the distance from zero," which is kind of true? But it's really for finding distances of any kind -- in fact, it's later used to mean exactly that when you get into complex algebra (that is, algebra with imaginary numbers) and linear algebra (matrices and vectors).

But that's for later.