#math teaching

[sanktpolypenbourg]

As I said in a previous post, I have deep sympathy for the frustration of people who are good at math when they see math so almost universally hated by children and adults

And again and again, they try to explain that math is very much within everyone's reach and can be fun and, at least in western countries, education was to blame, messing up this very doable and fun thing by teaching it wrong

But I still gotta wonder - why math? If it is really just education messing this up, why does it mess up so much with math, specifically? I'm sorry but I still cannot shake the sense that even if it's just bad teaching, math is especially vulnerable to bad teaching.

Or is it maybe just that math is the only truly exact science, so there is no margin of error, so unlike every other field where you can sortof weasel around and get away with teaching and retaining half-truths and oversimplifications and purely personal opinions, math is unforgiving with the vague and the incorrect?

[maths-screaming]

Well That Sucks, Thanks for the Memories

(Bonus points if you can name the anime from whose blooper reel I got the title of this post. No really - it became a part of my personal meme lexicon in the early 2000s from an anime dub blooper reel, and for the life of me I cannot remember which anime it was. Now that we've gotten the depths of my sad nerdery out of the way, let us talk about how much I suck at math.)

Like everyone else in a US high school the last week before break, I did not do much actual work the last week before break. I handed out a lot of candy canes and shelved a few books. I made a to-do list of projects that are Next Year Me's Problem. And I Googled "dyscalculia."

This isn't the first time I've looked up "dyscalculia," but it was the first time I did so on a mission: to do anything at all other than throw my hands up and go "welp, brain broken, too bad no numbers for me."

So I started looking at books and articles on dyscalculia. I read about how to build adaptation skills in kids that have it and how adults can adapt to it too. I learned that not everyone with math anxiety has dyscalculia, but everyone with dyscalculia has math anxiety.

And I learned that, with or without a numbers learning disorder, the way I was taught arithmetic was probably the worst possible approach offered in the entire previous century.

Let me back up.

The current "gold standard" for teaching math to kids is the CPA approach. It stands for Concrete, Pictorial, Abstract - the sequence by which new ideas are introduced. (It's also called the CRA approach, for Concrete - Representational - Abstract.)

Teaching a kid how to count to 10? Hand them 10 of something. Have them move the pieces around, line them up, make groups. Eventually, add pictures of groups of things (apples, kites, washed-up baseball players). Later, add the number symbols we all know and love (in the US, 1, 2, 3, and the rest of the squad).

This is the cornerstone of the Singapore method, which consistently lands Singapore's students in the top math scorers worldwide - by a lot.

Above all, this method stresses, do not withdraw concrete and pictorial representations too soon. We're hard-wired as a species to like concrete counting methods. We have ten fingers, and we use them for more than picking our noses!

Flashback to my first grade classroom.

My first grade classroom had four or five abacuses - the kind with the rainbow beads on horizontal strings. Being a child whose favorite color was "rainbow," I loved these things. I would choose them over toys during playtime.

I was not allowed to use them for math lessons.

Why? Because the abacuses were reserved "for the slower kids" (my teacher's exact words). I was "very bright"; I "just needed to apply myself."

(As a multiply-neurodivergent adult who wasn't diagnosed with any of it until adulthood and as someone who works with high schoolers every day, let me just say: the phrase "you're smart, you just need to apply yourself" should be a one-way ticket to a full LD screening. #justeducatoropinions)

I had math anxiety by the end of first grade. Because "applying myself," whatever that meant, didn't bridge that gap between the concrete and the abstract. Numbers were weird alien symbols I could decode only occasionally. Sometimes they just wouldn't talk to me. I couldn't explain why. (I was six!)

Learning at age 42 that I was systematically deprived of the tools required to succeed in math from the age of 6 is doing a number on me. On that first day, I had to take a fast three laps around the high school track to calm down before my lunch break ended.

When I got back to my desk, I of course went looking for better textbook options.

I find the artwork the Maths - No Problem! series, part of the UK National Curriculum, weirdly soothing. It's cute and friendly. And the fact that every single lesson is modeled with little cubes reassures me that no one is going to make me rely solely on those devious little "digits" until I'm good and ready.

The series is also available for free on the Internet Archive. Since I'm not looking for the best books so much as something better than I had as a kid, I've decided to start here. With Book 1A.

Let's see what happens.

Further reading:

What is the Concrete Representationa Abstract (CRA) Approach and How to Use It In Your Elementary Math Classroom

What is Singapore Math?

Singapore Math (Wikipedia)

Maths - No Problem! Textbook 1A (Internet Archive)

[the-math-hatter]

The textbook mentioned My Youtube Channel

[for-the-win13]

CRITICAL REALISM AND PANDEMIC TEACHING

Tentative Research Question: How did teachers creatively strategize to deliver Mathematics learning during the pandemic?

Critical Realism as a meta-theory is pertinent to generate meaningful and impartial interpretations and conclusions. It posits that the world is intransitive, stratified, works as an open system, and is emergent. It demonstrates a harmonious balance between Ontological Realism and Epistemic Relativism. A researcher who subscribes to this theory values sound methodologies and comprehensive analysis before making interpretations. Critical realist researchers understand the plurality of ideas and adhere to certain standards to develop the most logical conclusions. I intend to apply this meta-theory in my present and future research endeavors.

My present research project covers Mathematics teachers' experiences in distance education during the COVID-19 pandemic. It aims to determine the creative teaching strategies that Math teachers implemented despite the challenges and restrictions brought by the pandemic. This paper explains the assumptions of Critical Realism and its implications in my research project. This paper discusses how Critical Realism influenced my research decisions.

The world is intransitive, but the knowledge about the world is transitive.

Ontological Realism is a significant part of the triumvirate of Critical Realism, asserting that the world is autonomous of the knower. It explains why judgement is possible. On the other hand, Epistemic Relativism states that human knowledge is dependent on the knower. It asserts the plurality of interpretations and perspectives that underscore the need for judgment.

The assumptions of Ontological Realism and Epistemic Relativism emphasize the need to do research and commit to making rational judgments. Although the world is intransitive, the knowledge about the world is transitive. Our understanding of the world is constructed from our perceptions and perspectives. This assumption should inspire all researchers to use the most appropriate methods and the right analytical framework to acquire a more comprehensive knowledge of the world. Notably, this assumption should teach humility to any researcher. Regardless of the sophistication of the implemented research methods, all research studies will only uncover fractions of the truth.

Critical Realism is a potent framework for studying how teachers creatively strategize to deliver Math lessons during the pandemic. The idea that the world is transitive posits that knowledge about the world is bounded and necessitates the practice of judgmental rationality. With the limitations of knowing, the selection of the most suitable research methods is critical. Anchored on the assumption of intransitivity, I intend to employ a combination of qualitative and quantitative methods in my research project. The inclusion of qualitative methods provides an in-depth explanation of an existing phenomenon. The combination of qualitative and quantitative methods is a big help in practicing judgmental rationality. It will lead to more comprehensive information about the experiences of Math teachers during the pandemic.

The world is stratified into domains of empirical, actual, and real.

Critical Realism claims that the world has different but distinct domains: the empirical, the actual, and the causal (Schiller, 2016). According to Allana and Clark (2018), human perception and personal experiences define the empirical domain. In this domain, knowledge is derived from what is perceived and what generates an effect. Schiller (2016) asserts that the actual domain covers all events that occur regardless of whether they are perceived or experienced. Meanwhile, according to Allana and Clark (2018), the real domain includes the causal powers that affect events in the actual and empirical domains.

 One significant impact of this worldview is the idea that reality is not limited to human perception and personal experiences. The stratification is a substantial rationale for conducting research in pursuit of a deeper understanding of the causal domain. Within the scope of my research project, I intend to transcend the empirical and actual domains. Some studies asserted the factors that affect teaching experience during the pandemic. Akar and Erden (2021) found that distance education limits teachers in motivating students, providing adequate feedback, and facilitating communication and interaction. Fakhrunisa and Prabawanto (2021) discovered issues involving the readiness of teachers to use online applications, limitations in student access to learning resources, problems in facilitating mathematical thinking processes, and limitations in providing feedback. Although some studies covered the factors that affect the teaching experiences of Math teachers during the pandemic, these research papers did not investigate the interrelation of factors. Given this gap, I intend to examine the experiences of Math teachers during the pandemic and determine how different factors interplay and profoundly impact the decision to implement creative teaching strategies.

The world is an open system.

After writing the draft of my review of related literature for my research project, I noticed the permutation of factors that define the experiences of teachers and students in the context of distance education during the pandemic. Some research studies highlighted the benefits and opportunities of distance education (e.g. Hebebci et al., 2020; Aksan, 2021; Lavidas et al., 2022). Some research studies identified the issues and challenges (e.g. Aldon et al., 2021; Roman, 2021; Akar & Erden, 2021).

 The difference in findings indicates that the world is an open system. Multiple causes interplay and determine an event. The difference in results can be attributed to the difference in various factors. For instance, the difference in preferred learning modality of teachers and students after the pandemic may be influenced by the diversity in readiness level, available resources, quality of support, and other factors. The study of Ince et al. (2020) discovered the views of students on distance learning are determined by their access to gadgets and the availability of an Internet connection.  Students who are more active in online classes are the students with better access to gadgets and the Internet. Although the studies have similar contexts, learning modality and the global pandemic are only two of the many factors that impact teaching and learning.

There are two significant implications of the notion of an open system in my research project. First, a mixed-method approach is essential to examine different factors and their interconnection. According to Clark et al. (2008), explanatory studies necessitate a combination of both qualitative and quantitative methods. The assumption that the world is an open system explains why qualitative methods are appropriate in examining how Math teachers creatively strategize. Experimental control is not possible in an open system. If exclusive causality is absolute, there is no need to do interviews and observations because a single statistical test would suffice. Given that multiple factors influence an event, a mixed-method approach is needed to cover the complexities of the teaching experience during the pandemic. The second implication is on the application of the results in other disciplines. The findings of my research project on teaching experiences may be recommended to other subject areas and disciplines. Since multiple variables are interconnected in an open system, my findings may contribute to studying other phenomena. The results may serve as a reference for future research studies.

The world is emergent.

It is assumed in Critical Realism that the world is emergent. The multiple factors that influence an event in an open system have distinct levels: physical, biological, psychological, social, and cultural.

In the context of pandemic teaching, the experiences during the pandemic are affected by several factors. Aldon et al. (2021) found four that define the teaching experience of Mathematics teachers: management of learning sessions, implementation of assessment, addressing student problems, and providing instructional support. These factors belong at distinct and different levels. The experiences of teachers in managing learning sessions and implementing assessments are products of the existing cultures and values. The objectives, decisions, and performance of teachers during the pandemic are influenced by their mental state and physical condition, and the well-being of the people around them.

The assumption that the world is emergent made me understand that studying teaching experiences is more than just gathering data about teachers. With this assumption, it is recommended to design research instruments in a way that covers the various aspects of teaching and the different factors that impact teaching experience. In my research project, I intend to examine how factors related to teachers, students, and the learning environment interact and impact the implementation of creative Math teaching strategies.

Summary

            The assumptions of Critical Realism had a significant influence on the decisions that I made for my research project, and I intend to continue utilizing these assumptions in my next decisions. The belief in the intransitivity of the world is a reminder of the limitations of research studies and the importance of selecting the most appropriate methods to uncover the truth about pandemic teaching. The idea of stratification motivates me to go beyond the empirical domain by examining the interrelation of factors that impact teachers during the pandemic. Furthermore, the viewpoint that the world is an open and emergent system demands a mixed-method approach to obtain more comprehensive information on how Math teachers creatively deliver math lessons during the pandemic.

REFERENCE

Allana, S. & Clark, A. (2018). Applying Meta-Theory to Qualitative and Mixed-Methods Research: A Discussion of Critical Realism and Heart Failure Disease Management Interventions Research. International Journal of Qualitative Methods. 17, 1-9. https://doi.org/10.1177/1609406918790042

Sage. Schiller, C. J. (2016). Critical Realism in Nursing: An Emerging Approach. Nursing Philosophy, 17, 88–102

Yohannes, Y., Juandi, D., Diana, N., & Sukma, Y. (2021). Mathematics Teachers' Difficulties in Implementing Online Learning during the COVID-19 Pandemic. Journal of Hunan University（Natural Sciences). 48(5), 1-12. https://www.researchgate.net/publication/352290221_Mathematics_Teachers'_Difficulties_in_Implementing_Online_Learning_during_the_COVID-19_Pandemic

Sugilar, Rajati, J., & Achmad (2021). A Hierarchical Component Model of Students’ Difficulties of Learning Mathematics in a Distance Higher Education. Journal of Physics: Conference Series. https://doi.org/ 10.1088/1742-6596/1918/4/042053

Hebebci, M. T., Bertiz, Y., & Alan, S. (2020). Investigation of Views of Students and Teachers on Distance Education Practices during the Coronavirus (COVID-19) Pandemic. International Journal of Technology in Education and Science. 4(4), 267-282. https://doi.org/10.46328/ijtes.v4i4.113

Aksan, J. A. (2021). Effect of Modular Distance Learning Approach to Academic Performance in Mathematics of Students in Mindanao State University-Sulu Senior High School Amidst COVID-19 Pandemic. Open Access Indonesia Journal of Social Sciences, 4(4), 445-467. https://doi.org/10.37275/oaijss.v4i2.64

Lavidas, K., Apostolou, Z., & Papadakis, S. (2022) Challenges and Opportunities of Mathematics in Digital Times: Preschool Teachers’ Views. Educ. Sci. 2022, 12(7), 459; https://doi.org/10.3390/educsci12070459

Aldon, G., Cusi, A., Schacht, F. & Swidan, O. (2021). Teaching Mathematics in a Context of Lockdown: A Study Focused on Teachers’ Praxeologies. Education Sciences. 11(2), 1-21. https://doi.org/10.3390/educsci11020038

Roman (2021). Experiences of Teachers on Using Modular Distance Learning (MDL) in Teaching Mathematics During the COVID-19 Pandemic Southeast Asian Journal of Science and Technology. 6 (2),78-86. https://www.researchgate.net/publication/357957500_Experiences_of_Teachers_on_Using_Modular_Distance_Learning_MDL_in_Teaching_Mathematics_During_the_COVID-19_Pandemic

Akar, S. S. & Erden, M. K. (2021). Distance Education Experiences of Secondary School Math Teachers During the Pandemic: A Narrative Study. Turkish Online Journal of Distance Education. 22(3). https://dergipark.org.tr/en/download/article-file/1857612

Fakhrunisa, F. &  Prabawanto, S. (2021). Online Learning in COVID-19 Pandemic: An Investigation of Mathematics Teachers’ Perception. http://dx.doi.org/10.1145/3439147.3439179

Ince, Y. I., Kabul, N., & Kabul, A. (2022). Opinions of High School Students about Distance Education in Pandemic Process. Journal of Learning and Teaching in Digital Age. 7(2), 192-199. https://files.eric.ed.gov/fulltext/EJ1350878.pdf

Aldon, G., Cusi, A., Schacht, F. & Swidan, O. (2021). Teaching Mathematics in a Context of Lockdown: A Study Focused on Teachers’ Praxeologies. Education Sciences. 11(2), 1-21. https://doi.org/10.3390/educsci11020038

[algebra-as-praxis]

First post!! I wanted to show you how deep a rabbit hole you can dig with a very simple concept like, "What does 'four' mean?"

I have a number line.

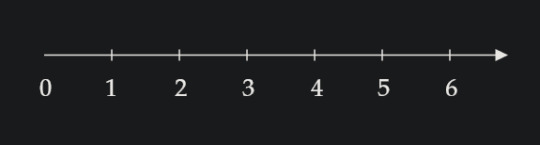
So, I'd like you to imagine that you've sat down across from me on your first day in class, and I put some kind of math worksheet with this number line on it that gives you a very simple-sounding task: "Circle four."

If you are like nearly every one of the older students I've had, you'll circle the number 4 on the line. And I'd say something like, "That is a perfectly reasonable response to this request. There is nothing wrong with what you've done. But aren't you suspicious about how simple this question sounds? Did you see that there was a twist coming?"

On a number line, the place where we've written 4 is not actually the value 4. It is more like the position 4; we would call this the ordinal number (a number used to track the positional order of things; another example of an ordinal number is the word "fourth," which tells you that there are three other things before that one).

So, if you just circled the number 4, you definitely circled the position, but the thing you circled isn't worth 4. If you were going to circle the thing that has the value (or cardinality, since we're counting individual objects) of 4, it would look something more like this:

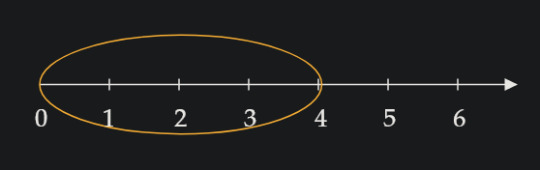
This is because in order to have the value of 4, you need everything that came before it! Imagine counting out candy while your kid sister steals and eats the candies you counted already. When you get to your final number, that number is not how many candies you have, but rather how many you counted cuz your sister's got 'em all! For the value of your candies to stay the same, you need all of them to be there!

"Four" could also look, less straightforwardly, like this:

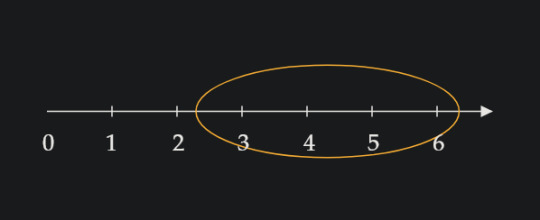
The distance from the start of the circle to the end is four; and since we're circling the line, the length of the line that is circled is four. If we imagine the circle starts (from the left) at the position of 2.3, it would have to end at the position (from the right) 6.3. If we find the difference of the numbers at these positions, we would be doing the equation 6.3 - 2.3 = 4.

A quick summary:

The position of a number is shown with an ordinal number.

The actual physical quantity of the individual items is shown with a cardinal number, which we more typically call the value.

We can find a value inside the ordinals by finding the distance between any two ordinals, via subtraction.

Okay... But notice we've used two words here that seem to imply the same thing: difference and distance. Let's clear this up real quick:

Difference is the result of subtraction. Generally, if we want to find the difference between two things, we subtract the first thing from the second thing:

second - first = difference

But that's not a rule, so much as a norm. In reality, if you wanted to find the difference of two numbers, the person asking had best be very clear which way they want you to do it, because if you reverse this you will get the negative of the result above!

For example, if you were asked to find the difference between 6 and 15, you would do 15 - 6 = 9. But if it's not clear and you instead did 6 - 15, you get -9.

If, however, someone wanted to know how far apart these two numbers are, they would not be asking the difference but rather the distance between these numbers. The result would therefore be the absolute value of either one of these subtractions:

|15 - 6| = |9| = 9, |6 - 15| = |-9| = 9 Same result!

This is in actuality the real use of absolute values. Absolute value is typically shown as "the distance from zero," which is kind of true? But it's really for finding distances of any kind -- in fact, it's later used to mean exactly that when you get into complex algebra (that is, algebra with imaginary numbers) and linear algebra (matrices and vectors).

But that's for later.

[nfinitefreetime]

And here we go

I would typically expect to be Sundaying pretty hard at the end of Spring Break, but that’s not what’s happening. I’m not stressed at all. That said, I’ve had one hell of a time figuring out what the hell I’m going to do with my students this week, and more specifically what I’m going to do with them tomorrow, and I finally settled on a super basic, 20-question paper assignment with a mix of…

[noodles-and-tea]

I am once again back with my Stan Pines is smart agenda

[cosmetichorror]

Lu au where everyone is the age of their game

Wild is 7

Warriors is 10

Sky is 13

Twilight is 18

Four is 20

Wind is 22

Time is 26

Legend is 33

Hyrule is 37

Warriors and Wild are LITERALLY child soldiers, Sky is in middle school (and is more than happy to travel as it means he has less homework to do…)

Twilight is a fresh adult and doesn’t know what he’s doing with his life

Four is still as short as he is in the comic. Also much to Sky’s dismay Four basically becomes his teacher so he doesn’t fall behind in his studies.

Wind finally can legally drink…. He’s the wine aunt. He’s a nut case. The kids love him. He and Time were babysitting Warriors during the WAR and they’re both still mad they put a like, 9 year old into a war.

Time is freshly married…. He’s as bad (if not worse) then Sky ever could be when it comes to being lovey dovey.

Legend is mad he has to go on another adventure after he’s been comfortably retired for a decade. He becomes the new old man, despite Rulie being older…. And btw Hyrule is still his little brother.

Hyrule is aging wonderfully much to everyone’s surprise. He looks 25. He still can’t read btw but he has mastered life in the wilderness. He is like a mountain lion, he can hide behind anything and sneak anywhere now. Give him a leaf and he’ll find a way to hide behind it and you’ll never see him….

They would’ve never found Hyrule if they didn’t have Warriors and Wild with them, and even then them finding Hyrule was more so Hyrule allowing them to find him so he could check on the kids.

[standingappa]

headcannon that albus is a math genius he just never knew because they don’t teach fucking math at hogwarts

[spirkbitch]

(Didn’t include tas since it’s pretty much just tos but animated)

Put in the tags what you think your job/role would be too (because I think it would be fun)

[1neptia]

Moriarty teaching an ACTUAL mathematics lecture? :]

Professor Moriarty teaches you advanced calculus

An online geometry lecture

I know this has been in my asks inbox in a while & finally finished cooking

[reality-detective]

Mathematics 🤔

[algebra-as-praxis]

Factors, Terms, and Exponents

When you learn exponents in school, the language we tend to get taught about them is actually very unclear and can lead you to make mistakes and misunderstand the concept entirely. I intend to clean this up from the bottom floor.

I: Types of Math Problems

(we're gonna gloss over things like proofs and logic, this is just about algebra and arithmetic)

A math problem is more accurately called a statement. Statements can be expressions, equations, or inequalities. Both equations and inequalities are comparisons.

Any statement can either be true or false. Unless we are otherwise asked to figure out the factual nature of the statement, typically we just assume any statement given to us in math class is true.

An expression is any statement about how you'd like numbers to interact, but excluding the actual result of that interaction. For example, if I said I was going to buy two sandwiches at $4 each, we would understand the cost of that as being found with the expression 2 × 4.

Algebraically, if we have some unknown value but we know things we want to do with it, we can use an expression to show that interaction without bothering to find the unknown value yet. If I have x dollars in my pocket and I know every piece of candy I want to buy is 50 cents, I could write the expression x/0.5 to show the amount of candy I could buy; then, when I finally check my pocket to see how much money I have, I could solve it. And I could use that same problem any day, since I have the setup for the problem already.

An equation is a statement that sets two expressions equal in value to each other. An equation is most easily identified by the inclusion of an equal sign: =

Equations are split between its sides -- the expression on the left side of the equal sign, and the expression on the right side of the equal sign. So, in the equation 3x + 4 = 17 + 5x we can see the left side is 3x + 4 and the right side is 17 + 5x, and the equal sign is simply telling us that these two expressions have the same value.

An inequality is a statement that tells you that two expressions are not equal, and in which way they are not equal. Inequalities can tell you that one side is greater than the other, or simply that they aren't equal. They can also tell you that they may be equal but also one side might be greater.

You can use > to mean the left side is greater than the right side, or < to mean the left side is less than the right side. You can also use either of these with a line underneath to show that they are "greater than or equal to" or "less than or equal to," like so: ≤ ≥

And if you use any inequality sign and put a slash through it, or even the equal sign with a slash through it, you are negating that sign, meaning it will be the exact opposite of what it normally means: an equal sign with a slash through it (≠) means "not equal to," whereas a less than sign with a slash through it (≮) means "not less than" (which is equivalent to "greater than or equal to").

Interrupting for a moment: There's this thing called the Law of Trichotomy ("trichotomy" means "three distinct possibilities"), which states that in any comparison of two values, exactly one of three things is true: the first value may be equal to the second value (x = y), or it may be greater than that value (x > y), or it may be less than that value (x < y). This also accurately implies that these are the only three comparative states of values.

This can be confusing the first time you hear it since you know about "greater than or equal to," which sounds like it implies two at once. But remember, the "or" does not mean "both at once." It in fact means "only one of these is true, but they are both possible."

II: Values, Factors, Terms

Every expression has a value. All values are made of one or more terms. And all terms are made of two or more factors.

Once you've performed all of the operations in an expression, you are going to be left with a single number. That number is the expression's value. But notice to find the value we had to actually do all of those operations. The value, therefore, is the result of all of those operations on those numbers.

The expression is split up into smaller values, called terms, which are groups of multiplication and division. Terms add/subtract with other terms.

So, for example, if we have the expression 3 × 12 + 7, there are two terms: 3 × 12 is the first term, and 7 is the second term. Notice that the two terms are separated by a plus sign: +. This is because all terms add/subtract, so you can think of the plus sign as being the thing that separates a problem into its individual terms.

Terms can have subterms. For example, in the term 3(17 - 2), there is a parenthetical statement, 17 - 2, which contains two terms, 17 and -2. Because those two terms exist inside of a term, they are this term's subterms. Likewise, we can call the term that contains these two terms their superterm.

Because terms are groupings of multiplication and division, the numbers you are multiplying and dividing by are that term's factors. Factors multiply in the same way that terms add. So, in the expression 3 × 12 + 7, there are two terms, 3 × 12 and 7, and in the first term you have two factors, 3 and 12; likewise in the second term you have "two" factors, 1 and 7.

IIa: Terms of 0, and Factors of 1

There are what I call "null operations," that is, an operation using a number that has no effect on a problem's value. For addition and subtraction, it's 0. You can add or subtract 0, and it doesn't do anything. For multiplication and division, it's 1; if you multiply or divide by 1, nothing changes.

Because of this, every problem you've ever done technically has an infinite number of these "plus zero" and "times one" operations hiding everywhere (zero property of addition and one property of multiplication). We just don't usually write it cuz... they don't tend to do anything.

But in the example above, we have the term 7. But to describe that number as factors, we said 1 × 7. This is because factors always multiply. But if there's no number next to 7, then what would it be multiplying? It must be 1 × 7, then.

This will come up soon, and is actually very important.

III: Exponents

We use multiplication as a stand-in for repeated addition. 3 + 3 + 3 + 3 + 3 is annoying to write, so instead we notice that we wrote 3 five times, and thus we can say 5 × 3. ----- "Wait why'd you write it in this order?", you might ask of me. "Five times three" has a missing word. It is actually "Five times of three." It's telling me what I have five of. Yes, it is totally acceptable to write 3 × 5, you can multiply numbers within a term in any order (associative/commutative properties of multiplication) but the language itself would imply 5 × 3.

So, like we use multiplication to simplify repeated addition, we need a way to talk about repeated multiplication. That's where exponents come in. Instead of 7 × 7 × 7 × 7, we can write 7⁴, read "seven to the fourth power," which gets shortened to "seven to the fourth." The four, written in superscript (super- as in above, -script as in writing, so "writing above"), is the exponent; the number it is next to is called the base of that exponent. Exponents indicate how many times a particular factor (the base of the exponent) exists in a term.

Notice this definition is different from what you're taught in school. In school, the definition you're given is "multiplied by itself this many times." But that's not a good description, and in fact the language there doesn't even accurately describe what's going on (if you multiply something by itself x times, you have x+1 of that factor, which is not what is going on).

IIIa: Prime Factorization

What we might consider the best way to represent the factors that make up a term is called prime factorization, where we list the prime numbers we'd have to multiply together to get the value of a term. Obviously this doesn't work for every number, but any integer (whole number) or rational number (fraction, terminating decimal, or repeating decimal) can be expressed this way.

Let's try this with the number 144:

144 = (4 × 36) = (2 × 2) × (6 × 6) = 2 × 2 × (2 × 3) × (2 × 3)

Rearranging the factors so all the common factors are next to each other: 2 × 2 × 2 × 2 × 3 × 3. There are four 2's, and two 3's. Therefore, the prime factorization is 2⁴ × 3².

We're gonna continue this next time, going deeper into exponents.

[nfinitefreetime]

Three down, one to go

I applied to teach summer school, did I mention that? I don’t know for sure that I want to do it, but I can’t decide that I do want it unless I apply now, and I have no real sense of how many jobs there are or what my chances are to get one, because for this type of thing they basically drop the teachers into a spreadsheet that sorts us by seniority and licensure and stuff like that and then…

[vesna-v-irkutske]

In the 6th grade Nikita was enrolled in a math class. But he didn't gravitate towards science.

Marina Lytkina recalls: "The teacher had no pedagogical education, she's a programmer. And she interacted with the children as if they were students, she didn't explain anything to them. She corrected mistakes in the notebooks and said that they should have listened in class. People have never understood that he's not like everyone else: he will never ask for anything, always silent. Nikita stopped studying in the 8th grade. He began to skip classes, including in the main subject — mathematics. But back then, he was still listening to me."

But soon Nikita stopped obeying his mother. He studied at the energy college for a some time. He was expelled from there after failing the first midterm exams. The following year, in September 2010, he began attending classes at the construction college. Two months later, he and Artyom went on their first hunt.

The energy college. The construction college.

Studying at the construction college turned into trouble.

Marina Lytkina: "At first, Nikita was teased and bullied. And then they started extorting money from him. Then he was patronized by one of his classmates, and in return, together with the older guys, he demanded money — in other words, he engaged in extortion. They came to our apartment together and took everything they found. First, they took some money, then they took my walkman, and the last time they stole the gold. Nikita followed them like a steer. It was impossible to hide the loss. I found out everything and called the police. A criminal case was opened."

Later, Marina recanted the statement to the police — she didn't want that boy to be imprisoned.

One of Nikita's college classmates, talking about him. Read it from the bottom up.

[soppsop]

i really like ringo