blog-normal-distribution

[blog-normal-distribution]

they schramm on my loewner till i evolve

she brownian on my loop till i soup

[blog-normal-distribution]

he liouville on my gravity till i quantum

she brownian on my loop till i soup

[blog-normal-distribution]

she brownian on my loop till i soup

[blog-normal-distribution]

screw it. biblically accurate angle

[blog-normal-distribution]

Mathematicians be like:

Def 1.1: A function f is fucked-up iff it is not Lebesgue measurable

Def 1.2: A function is evil iff its graph has non-integer Hausdorff dimension.

Exercise 1: Prove that there exist fucked-up and evil functions

[blog-normal-distribution]

you know what? fuck you *replaces all the boards in your ship with different boards until you aren't sure whether it's the same ship anymore*

[blog-normal-distribution]

[blog-normal-distribution]

new personality test I guess

[blog-normal-distribution]

[blog-normal-distribution]

u tellin me a brain ate these amoebas? 🤨

[blog-normal-distribution]

*buys a box of hagomoro chalk* *eats a stick of hagomoro chalk* *eats a stick of hagomoro chalk* *eats a stick of hagomoro chalk* *eats a stick of hagomoro chalk* *eats a stick of hagomoro chalk* *eats a stick of ha

[blog-normal-distribution]

Link / Link

[blog-normal-distribution]

Saturn's rings via @astrophosnap[1st: digital CGI]& @bitsofsaturn

[blog-normal-distribution]

(observes you)

[blog-normal-distribution]

I'll be continuing on to a maths masters next year!!! It's been a primary goal of mine for a long time to do Part III and after an entire day stressing about results day (the department gave a six and a half hour window in which results could've come out and they were still released 15 minutes AFTER the upper bound) I can safely say I qualified for the 4th year!!

Luckily this means that I'll be able to post more now, now that exams are done and results are out xoxo (but I probably still won't post that regularly oops)

[blog-normal-distribution]

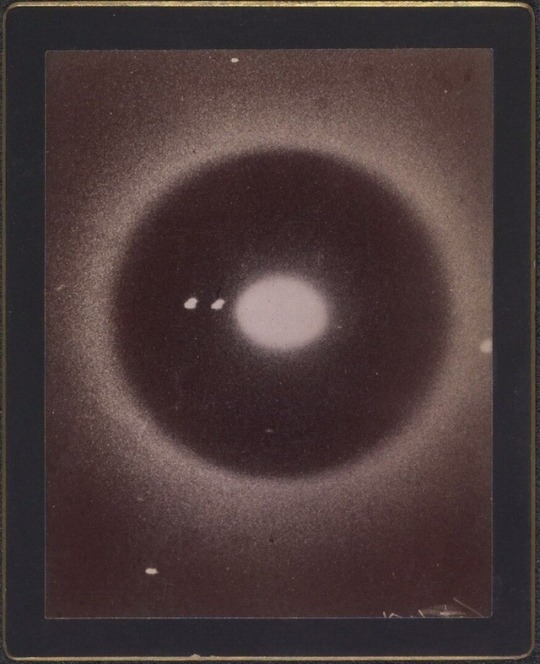
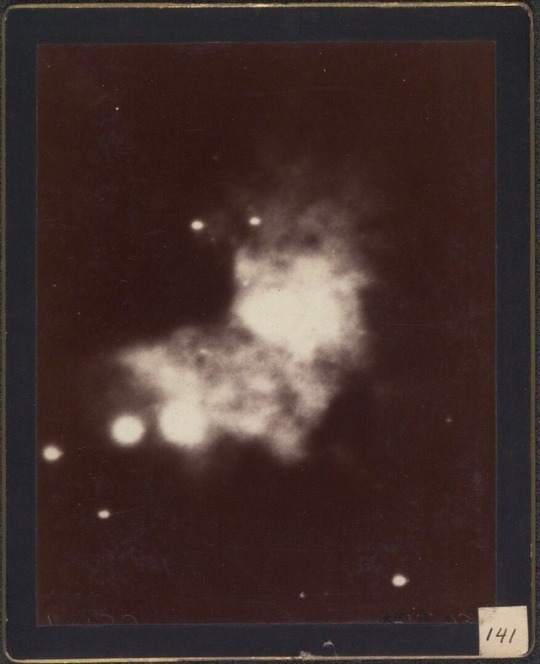
Astronomical photographs, Harvard College Observatory, Cambridge, 1890-1920

[blog-normal-distribution]

This is a really great puzzle and I recommend that anyone who hasn't seen a solution before try and solve it! As a hint, you'll need to use the axiom of choice, and equivalence relations. You'll also need to assume that everyone can see all the hats except their own.

Anyways here's the solution:

Assign each person a natural number* 1, 2, 3, 4,... and consider all possible 'colourings' of the naturals* (that is, ways to assign red and blue to each number). We define an equivalence relation on these colourings, where two colourings are equivalent if they differ at only finitely many numbers. This equivalence relation splits the set of colourings into disjoint equivalence classes. Now, the mathematicians use the axiom of choice to pick a representative colouring from each equivalence class.

Now, when the dictator comes along and puts a coloured hat on everyone, get all of the mathematicians to stand in order, and look at everyone else's hats. Since the only hat they can't see is their own, they'll be able to deduce which equivalence class of colourings they're in. Then each mathematician just says the colour assigned to their number from the representative of this class!

*the variation I had seen of the puzzle had countably many people. But upon consideration, since we're already using the axiom of choice, I do beleive we can extend this to an arbitrary infinity of people just by invoking the well ordering principle to well-order all the mathematicians, indexing with ordinals.

This is one of my favourite puzzles and was in a problem sheet I had in my first year of uni! It was an optional question and was on an entirely different calibre to the ones we were expected to be able to figure out, and I personally never knew the solution until I had my friend explain it to me two years later.

Fun (infuriating) fact. If a dictator has an infinite number of mathematicians imprisoned, and places a red or blue cap on each one's head, and requires them all to guess what color their hat is at the same time without communicating, and will free them only if finitely many of them guess wrong, and will execute them otherwise, it's possible for them to come up with a strategy beforehand which guarantees they can go free.