champak30

[champak30]

What is a Straight Line in Mathematics?

Introduction:

 The concept of What is a straight line in Mathematics? is foundational. It is one of the simplest and most fundamental geometric shapes, yet its implications and applications are vast and profound. In this article I will try to explain into the concept of what is a Straight Line in Mathematics, exploring its definition, properties, equations, and significance in various mathematical contexts.

Explanation:

Definition of a Straight Line:

 In geometry What is a Straight Line?  is an infinite set of points which can be extended in both directions without any curvature. It has no thickness, no width, and no height; it is one-dimensional. The straight line is often considered the shortest distance between two points, a concept that is both intuitive and mathematically rigorous.

Historical Perspective:

The study of straight lines dates back to ancient civilizations. Euclid, a Greek mathematician, provided a systematic study of geometry in his work "Elements," where he defined a straight line as "a line which lies evenly with the points on itself." This definition, though simple, encapsulates the essence of straightness—consistency and uniformity in direction.

Basic Properties of a Straight Line:

1. Linearity

A straight line is characterized by its linearity, meaning it does not curve or bend. This property can be observed by plotting the line on a Cartesian plane, where it appears as a continuous line extending infinitely in both directions.

2. Infinite Length:

A straight line can be extended infinitely in both directions. This infinite nature is a key property that distinguishes lines from line segments, which have defined endpoints, and rays, which extend infinitely in only one direction.

3. No Thickness:

A straight line is one-dimensional. It has no thickness or width, making it an idealized geometric object. In practical terms, when we draw a line on paper, it will have some thickness, but mathematically, a line is considered to have zero width.

Equations of a Straight Line:

The representation of straight lines using equations allows for a precise mathematical description. There are several forms of the equation of a straight line, each with its own advantages depending on the context.

a. Slope-Intercept Form:

The slope-intercept form is one of the most commonly used equations of a straight line. It is given by:

y= mx+c

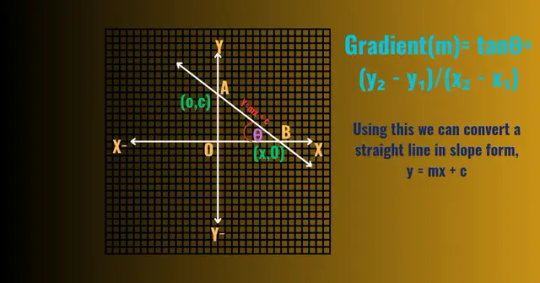
where m represents the slope or gradient of the line, Again m can be expressed as,

m = tanθ = (y₂ - y₁) / ( x₂- x₁),where θ = Inclination of the straight line,and(x₁,y₁), (x₂,y₂) are two points passes through the straight line.

and c represents the y-intercept. The slope m measures the steepness of the line, defined as the ratio of the rise (change in y) to the run (change in x). The y-intercept c is the point where the line crosses the y-axis.

For example, if we have the equation y = 2x+3, the slope(m) is 2, and the y-intercept(c) is 3. This means the line rises 2 units for every 1 unit it moves to the right, and it crosses the y-axis at the point (0, 3).

Some Problems related on Slope Intercept form of Straight line:

Question(1): The y-intercept and slope of a line is 5 and -1 respectively.Find the equation of the line.

Solution:  y-intercept(c) = 5

       Slope of the line (m) = - 1

∴ Equation of the line,

              y = mx + c

      => y = (-1)x + 5

      => y = - x + 5

    => x + y = 5

Question(2): If (2,3) and (-1,1) points lie on a straight line, find the slope of the line.

Solution:  ∵ x₁ = 2,   y₁ = 3

                   x₂ = -1,  y₂ = 1

     ∴ Slope of the line (m) = ( y₂ - y₁) /( x₂ - x₁)

                                         =  (1 - 3) /(-1 - 2)[putting values]

                                         = - 2/ -3

                                         = ⅔ 

b. Point-Slope Form:

The point-slope form is useful when we know a point on the line and its slope. It is given by:

y−y₁= m (x - x₁)

where (x₁,y₁) is a known point on the line, and m is the slope of the line.

For instance, if we know a line passes through the point (2, 3) with a slope of 4, the equation is:

y−3=4(x−2)

This can be simplified to the slope-intercept form if needed.

c. Standard Form:

The standard form of the equation of a linear straight line is:

Ax+By=C

where A, B, and C are constants. This form is particularly useful in solving systems of linear equations and in integer arithmetic.

For example, the equation 3x+4y=12

represents a straight line. We can convert this to the slope-intercept form to find the slope and y-intercept:

As we have,

    3x+4y=12

=> 4y = - 3x + 12

=> y = - ¾ x + 12/4

=> y = - ¾ x + 3

So, the slope of the straight line is −3/4  and the y-intercept is 3.

Some Problems related on Straight line:

Question(a):Find the slope and y-intercept of the given line, - x + 10 = 5y

Solution:   ∵ - x + 10 = 5y

               => y = - x /5 +10/5

               => y = - ⅕ x + 2

now comparing the above equation with y = mx + c

we get,

 Slope (m) = - ⅕ 

and y-intercept (c) = 2

Question(b):Gradient of a line is 2 and passes through the point (-3,1),find the equation of the straight line.

Solution: ∵ Gradient of the line(m) = 2

                   point = (-3,1)

   ∴ Equation of the straight line,

           y - y₁ = m(x - x₁)

       => y - 1 = 2{x - (-3)} [putting values]

      => y - 1 = 2 ( x + 3)

     => y - 1 = 2x + 6

    => - 2x + y -1- 6 = 0

   => - 2x + y - 7 = 0, which is the required equation of the straight line.

Question(c): The gradient of a straight line is -1 and y-intercept is 3, find the equation of the straight line.

Answer: Gradient (m) = - 1

              y-intercept (c) = 3

∴ Equation of the straight line will be,

         y = mx + c

    => y = (- 1)x + 3 [ putting value]

   => y = - x + 3

Graphical Representation:

Graphing a straight line involves plotting points that satisfy the line's equation and connecting them with a continuous line. The graphical representation provides a visual understanding of the line's behavior and properties.

1. Plotting Points:

To graph a line, we can start by choosing values for x and calculating the corresponding y values using the line's equation. Plotting these points on a Cartesian plane and connecting them gives us the line.

For example, for the line y=2x+1, 

we can choose x values such as -1, 0, 1, and 2, and find the corresponding y values:

When x=−1,then from above equation we get, y=2(−1)+1 = - 2 + 1 =−1

When x=0,then from above equation we get, y=2(0)+1= 0 + 1 =1

When x=1,then from above equation we get, y=2(1)+1 = 2 + 1 =3

When x=2,then from above equation we get, y=2(2)+1= 4 + 1 =5

Plotting these points and connecting them gives us the graph of the line.

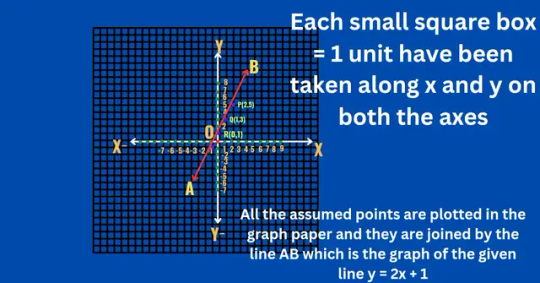
. Using Intercepts:

Another method is to use the x-intercept and y-intercept. The x-intercept is the point where the line crosses the x-axis, and the y-intercept is the point where the line crosses the y-axis.

The Intercept form of a straight line is ,

 x/a + y/b = 1,

where, a = x-intercept

           b = y-intercept

For example,Find x and y intercept of  the line 3x+4y=12

Solution:To find the x-intercept,we will take y=0 now the equation will become

3x+4(0)=12 

=>3x + 0 = 12

 =>3x =12 

 =>x= 12/3 

 =>x = 4 So, the x-intercept is 4

To find the y-intercept,we will take x=0,now the equation will become,

3(0)+4y=12

=>0 + 4y = 12

=>4y=12 

 =>y=12/4 

 =>y = 3 So, the y-intercept is 3

The above sum can be done in another way also,

∵ 3x+4y=12

=> 3x /12 + 4y / 12 = 12 / 12 [dividing bothsides by 12]

=> x/4 + y/3 =1 [Converting the given equation similar to x/a + y/b = 1]

∴ The x-intercept is 4

and the y-intercept is 3

Plotting these intercepts and connecting them gives us the graph of the line.

Some Problems related on Intercept of straight line:

Question(A):The x-intercept and y-intercept of a straight line are 2 and 3 respectively,find the equation of the straight line.

Solution:  x-intercept(a) = 2

                y-intercept(b) = 3

 As we know that intercept form of a straight line is,

            x / a + y / b = 1

        => x / 2 + y / 3 = 1 [putting values]

        => 6(x / 2 + y / 3) = 1X 6 [ As L.C.M of 2 and 3 is 6,so multiplying bothsides by 6]

       => 3x + 2y = 6, which is the required equation of the straight line.

Question(B): Find x-intercept and y-intercept of the given straight line, 3x - y = 12

Solution:     ∵ 3x - y = 12

                => 3x /12 - y/12 = 12/12 

                => x / 4 + y / (-12) = 1

Now comparing the above equation with x/a + y/b = 1 we get,

 x-intercept(a) = 4

and y-intercept(b) = -12

Slope of a Straight Line:

The slope of a straight line is a measure of its steepness and direction. It is a crucial concept in understanding the behavior of lines.

1. Definition of Slope:

The slope m of a line passing through two points (x₁,y₁) and (x₂,y₂) is given by:

m=(y₂- y₁) / (x₂- x₁)

This formula calculates the rate of change of y with respect to x.

2. Positive and Negative Slope:

A positive slope indicates that the line rises as x increases. For example, the line y=2x+1 has a positive slope of 2, meaning it rises 2 units for every 1 unit it moves to the right.

A negative slope indicates that the line falls as x increases. For example, the line y=−3x+4 has a negative slope of -3, meaning it falls 3 units for every 1 unit it moves to the right.

3. Zero and Undefined Slope:

A zero slope indicates a horizontal line, where y remains constant regardless of x. For example, the line y=5 is horizontal.

An undefined slope indicates a vertical line, where x remains constant regardless of y. For example, the line x=2 is vertical.

Parallel and Perpendicular Lines:

Now, we will understand the relationships between lines involve in  studying parallel and perpendicular lines.

1. Parallel Lines:

Two lines are parallel if they have the same slope but different y-intercepts. Parallel lines never intersect.

For example, the lines y=2x+1 and y=2x−3 are parallel because they both have a slope of 2.

Some Problems on Parallel Lines:

Question(x): Find a straight line which is parallel to the line 2x + 3y = - 1 and passes through the point (- 2, - 1)

Solution:   2x + 3y = - 1

             => 3y = - 2x - 1

         => y = - ⅔ x - ⅓ [dividing both sides by 3]

 ∴ gradient of the line (m₁) = - ⅔ 

∵ we will find a line which is parallel to the above line, then

                      m₂ = m₁ [ Let, m₂ is the gradient of the line which we will find]

                 => m₂ = - ⅔ 

Now, we will find the line which passes through the point (-2,-1) and has gradient - ⅔  also parallel to 2x + 3y = - 1

∴ Required straight line will be,

           y - y₁ = m (x - x₁)

       => y - (-1) = - ⅔ [x - (-2)]

       => y + 1 = - ⅔ ( x + 2)

      => 3(y + 1) = - 2 ( x + 2)

      => 3y + 3 = - 2x - 4

      => 2x + 3y + 3 + 4 = 0

      => 2x + 3y + 7 = 0

Question(y):Find the equation of straight lines which is parallel to x - 2y + 5 = 0 and at unit distance from the point (- 2, 2)

Solution: Let, the line parallel to x - 2y + 5 = 0 is x - 2y + c = 0

Now, the distance of the above line from the point = (Ax₁+ By₁+c) / ±√(A² + B²)

         = [1(-2) +(-2)2 +c] / √(1)² +(-2)² [ Here,A = 1,B = - 2, x₁ = - 2 and y₁= 2]

        = (- 2 - 4 + c) /±√1 +4

        = (- 6 + c) /±√5

Now, according to question,

      (- 6 + c) /±√5 = 1

 => - 6 + c = ±√5

=> c = 6 ±√5

∴ Required straight lines will be,

 x - 2y + 6 +√5 = 0 [ putting value of c]

and x - 2y + 6 -√5 = 0  [ putting value of c]

2. Perpendicular Lines

Two lines are perpendicular if the product of their slopes is -1. This means the slopes are negative reciprocals of each other.

For example, if one line has a slope of ¾ then the slope of perpendicular line of it will be - 4/3 

Some Problems on Perpendicular Lines:

Question(m): Find the equation of straight line which is perpendicular to the line 2x + 3y + 1 = 0 and passes through the point (2,1)

Solution:  ∵ 2x + 3y + 1 = 0 

              =>3y = - 2x - 1

              => y = - ⅔ x  - ⅓ [dividing both sides by 3]

∴ gradient of the line(m₁) = - ⅔ 

Let, the gradient of the line which is ⊥ to the given line = m₂

As, we know for two perpendicular lines,

     m₁ X m₂ = -1

  => - ⅔ X m₂ = -1 [ putting value]

 => m₂ = 3/2 

∴ Required equation of straight line will be

        y - y₁ = m₂ ( x - x₁)

     => y - 1 = 3/2 ( x - 1)

     => 2y - 2 = 3x - 3

     => 3x - 2y - 3 +2 = 0

     => 3x - 2y - 1 = 0

Question(n): Check whether given pair of lines are perpendicular or parallel,

                  3x - y + 2 = 0

                   x + 3y -1 = 0

Solution :  ∵ 3x - y + 2 = 0

                 => y = 3x + 2

∴ Gradient of the line(m₁) = 3

Again,  x + 3y -1 = 0

         => 3y = - x +1

        => y = - ⅓ x + ⅓ [dividing both sides by 3]

∴ Gradient of the line(m₂) = - ⅓ 

As, m₁ ≠ m₂

So, the given pair of lines are not parallel.

Again,

        m₁ x m₂

    = 3 x ( - ⅓)

    = - 1

So, the given pair of lines are ⊥ to each other.

To Read more....

[champak30]

Where Can I Get Phentermine to Lose Weight?

Introduction:

In the awarness for effective weight loss solutions, every person often find himself/herself exploring various options to achieve his/her fitness goals. Phentermine, a prescription medication known for its appetite-suppressant properties, has gained popularity as a potential aid in weight loss of body. However, the question that arises is, "Where can I get phentermine to lose weight?" Understanding the legal and safe avenues for obtaining phentermine is crucial for anyone considering its use as part of their weight loss journey.

Explanation:

 In this article I have given a brief description on

What is Pentermine ? and Where can I get phentermine to lose weight.

Understanding Phentermine:

Phentermine is a prescription medication classified as a sympathomimetic amine. It works by stimulating the release of certain chemicals in the brain that control appetite. As a result, individuals taking phentermine often experience a reduced desire to eat, which can contribute to weight loss when combined with a healthy diet and regular exercise.

Prescription Requirement:

One crucial aspect to note is that phentermine is not available over-the-counter. It is a prescription medication, meaning it can only be legally obtained with a prescription from a licensed healthcare provider. This requirement is in place to ensure the drug is used safely and under the supervision of a qualified medical professional.

Consulting a Healthcare Provider:

The first and most legitimate avenue for obtaining phentermine is through a healthcare provider or a registered physician. If we are considering using phentermine as part of our weight loss plan, schedule an appointment with our primary care physician or a healthcare professional specializing in weight management. During the consultation, our medical history, current health status, and weight loss goals will be evaluated to determine if phentermine is a suitable option for us or not.

It's important to be honest and thorough in discussing  our medical history, including any pre-existing conditions, medications, or allergies. This information helps the healthcare provider or physician  make an informed decision about whether phentermine is a safe and appropriate choice for our individual circumstances.

Prescription Options and Dosage:

If our healthcare provider determines that phentermine is a viable option for us, then he/she will prescribe the appropriate dosage based on our specific needs. It's crucial to follow the prescribed dosage and guidelines provided by our healthcare professional to ensure both safety and effectiveness.

To Read more...

[champak30]

What Is Sound Energy

Introduction:-

Sound is an integral part of our daily lives, whether we realize it or not. From the sweet melodies of a song to the cacophony of a bustling city, sound surrounds us constantly. But do we know what sound really is and how it relates to the concept of energy? Sound energy is a fascinating and important aspect of our world, and in this article, I will explain What is Sound Energy , how it is produced, transmitted, and detected, as well as its various applications and significance in our daily lives.

Explanation:-

To start, today's article  let's first know,

what is sound?

Answer:- Sound is a form of energy which gives us sensation to hear something.

What is wave ?

Answer:- When an external force is applied on a medium and it is disturbed,this disturbance of the medium which carries energy without any movement of particles is called wave.

What are the different types of waves?

Answer:- There are two types of waves:-

(i) Longitudinal wave (ii) Transverse wave

What is longitudinal wave?

Answer:- If the direction of propagation of a wave is horizontal to the direction of the particles of the medium through which wave propagates, is called longitudinal wave.

What is transverse wave ?

Answer:- If the direction of propagation of a wave is perpendicular to the direction of the particles of the medium through which wave propagates, is called transverse wave.

What is frequency?

Answer:- The total number of vibrations completes per unit time of a vibrational body, is called its frequency. It is denoted by the greek latter ν(nu) and its S.I unit is Hertz (Hz)

What is wave length?

Answer:- The distance between two consecutive crests or toughs(In case of transverse wave) or the distance between two consecutive compression or rarefaction (In case of longitudinal wave),is called wave length. It is denoted by the greek letter λ (lemda) and its S.I unit is meter.

What is time period?

Answer:- The time taken to complete one full oscillation of an oscillatory body is called time period. It is denoted by T and its S.I uni is sec.

Now we will know,

What is Sound Energy

Answer:-  In Physics,Sound energy is a form of mechanical energy that are formed from the vibration of matter, typically air, but it can also propagate through other materials such as water and solids. These vibrations create waves of pressure variations in the surrounding medium, which our ears detect as sound. Sound energy is a fascinating phenomenon because it involves the transfer of energy through the compression and rarefaction of particles in a medium, rather than the transfer of matter itself.

Some Problems of sound energy:

Question(1) The frequency of a vibrating string is 5 Hz  and its wave length is 3 m, find the velocity of sound in  the string.

To Read more....

[champak30]

Title: How to Find the Perimeter of a Triangle

Introduction:-

Triangles are one of the fundamental shapes in geometry. Understanding their properties and being able to calculate their various attributes is essential for both students and professionals and teachers in various fields. One of the most basic calculations for a triangle is finding its perimeter, which is the sum of the lengths of all its sides. In this article, I will try to explain into the various methods of How To Find The Perimeter Of A Triangle, including different types of triangles and the different cases to consider.

Explanation:-

Understanding the Basics Before I start this topic,How To Find The Perimeter Of A Triangle, let's establish a few key concepts and definitions:

Triangle Types: 

Based on sides triangles are divided in three categories:

(a)Equilateral Triangle: A triangle whose all three sides are equal is called equilateral triangle.

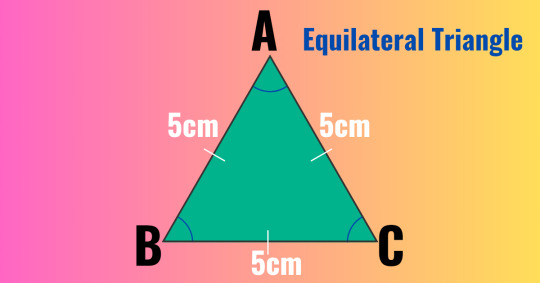
In the picture, ABC is an equilateral triangle,whose AB = BC = AC

(b)Isosceles Triangle: A triangle whose any two sides are equal and third one is different is called isosceles triangle.

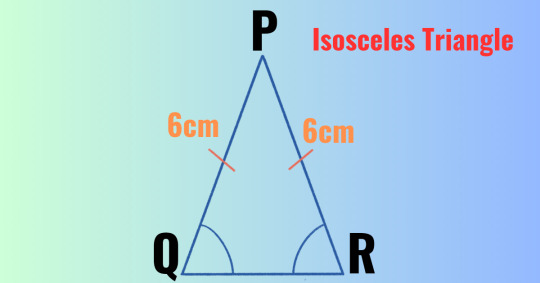
In the picture, PQR is an isosceles triangle whose   PQ = PR

(c)Scalene Triangle: A triangle whose all three sides are different to one another is called a scalene triangle.

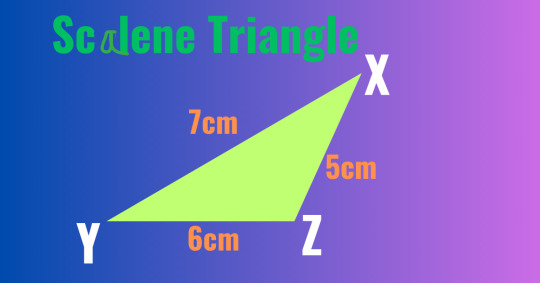
In the picture,  XYZ is a scalene triangle whose,   XY ≠ YZ ≠ ZX

Sides and Vertices:

(i)The sides of a triangle are the line segments that form the boundaries of the triangle. (ii)The vertices of a triangle are the points where the sides meet.

Perimeter:

The perimeter of a triangle is the total length or sum of all its sides.

Sides of a Triangle:

In an equilateral triangle, all sides have the same length, which we'll denote as 'a.' In an isosceles triangle, two sides have the same length, and the third side is 'b.' In a scalene triangle, all three sides have different lengths, which we'll denote as 'a,' 'b,' and 'c.' With these basic concepts in mind, let's discuss  How To Find The Perimeter Of A Triangle in various scenarios.

Procedure 1:

 Perimeter of an Equilateral Triangle: An equilateral triangle is a special case where all sides are of equal length. To find its perimeter, we  will simply multiply the length of one side ('a') by 3, as there are three equal sides. So,Perimeter of an Equilateral Triangle (P) = 3a

Some problems related on equilateral triangle:-

(a) The measure of each side of an equilateral triangle is 5 cm, Find its perimeter.

Solution:-

∵ Each side of the equilateral triangle(a) = 5cm ∴ Perimeter of the equilateral triangle = 3a = (3 × 5)cm = 15 cm (b) The perimeter of an equilateral triangle is 21cm, find its each side.

Solution:-

 ∵The perimeter of equilateral triangle = 21 cm ∴ Its each side measure = 21/3                                         = 7cm

Procedure 2: 

Perimeter of an Isosceles Triangle:

An isosceles triangle has two sides of equal length ('a') and one side of different length ('b'). To calculate its perimeter, we will add the lengths of the two equal sides ('a') and the different side ('b'). So, Perimeter of an Isosceles Triangle  (P) = 2a + b

Some problems related on isosceles triangle:

(a) The measure of two equal sides of an isosceles triangle is 7m each and third side is 5m, find the perimeter of the isosceles triangle.

Solution:-

∵ The measure of each equal side of the isosceles triangle(a) = 7m The measure of third side (b) = 5m ∴ Perimeter of the isosceles triangle = 2a + b = (2 × 7 + 5)m = (14 + 5)m = 19 m

To Read more....

[champak30]

(via GIPHY)

[champak30]

(via GIPHY)

[champak30]

View this post on Instagram

A post shared by Champak Jyoti (@jyotichampak30)

This is a Chemistry Story. To Read, please visit my profile https://www.instagram.com/p/CrvnKbzpJC6/?igshid=NGJjMDIxMWI=

[champak30]

Mathematics may not Teach us how to add happiness or how to minus sadness. But it does teach, Every Problem Has a Solution. To Read more.... bit.ly/3EVWOQR https://www.instagram.com/p/Crig_zdyeSK/?igshid=NGJjMDIxMWI=

[champak30]

View this post on Instagram

A post shared by champak jyoti (@champakjyoti2)

This is a science story on metalloids. To read please vist my profile. (at United States) https://www.instagram.com/p/CrPiY5TgVUa/?igshid=NGJjMDIxMWI=

[champak30]

This is a science story, To read it please visit my profile link is there. (at United States) https://www.instagram.com/p/CrOH0Jcyr3M/?igshid=NGJjMDIxMWI=

[champak30]

This is a science story.To read, please visit my profile. https://www.instagram.com/p/CqYZTvvS7ZB/?igshid=NGJjMDIxMWI=

[champak30]

This is a science story on electricity. To read please visit:- https://www.maths-group.online/2023/03/si-unit-of-resistance.html https://www.instagram.com/p/CqCKKZPy1gH/?igshid=NGJjMDIxMWI=

[champak30]

This is a voice to text converter tool, if you need more tools.Then please visit my profile,link is given there. https://www.instagram.com/p/CpSS1raymvI/?igshid=NGJjMDIxMWI=

[champak30]

This is a maths story.To read visit my profile. (at United States) https://www.instagram.com/p/CpPqu5LJuru/?igshid=NGJjMDIxMWI=

[champak30]

What are Powers in Math

Introduction:-

What are Powers in Math or we can say what are exponents in math is our  today's main discussion which is a very nice and an important topic of mathematics.

Explanation:- 

To start this discussion let us quick remember in general we find four operations in algebra and they are addition,subtraction,multiplication and division. Powers are associated with multiplication.Let us know, What are Powers in Math. Let,  us suppose,  aⁿ is an expression ,here 'a' is called base and n is  called exponent and aⁿ is the power of a in the expression.In another way we can explain that the total number of times when any number is multiplied itself is called its power .

 e.g;        3 × 3 × 3 × 3 × 3 = 3⁵ where, 5 is the exponent of base 3 and  3⁵ is the power of 3

Now we will know about formula of power.

The formulae of exponents :-

   (i) aⁿ × aⁱ = aⁿ⁺ⁱ

Rule(1):-

    In case of multiplication of exponents, If the bases are equal then powers are added.

(ii) aⁿ ÷ aⁱ = aⁿ⁻ⁱ

 Rule(2):-

In case of division of exponents,If the bases are equal then powers are subtracted.

(iii) a⁰ = 1

Rule(3):-

If any number has power zero, then result will be 1

(iv) a⁻ⁿ = 1/aⁿ

Rule(4):-

 If any number has power negative,then it will be 1 divides the number withe power to make it positive.

(v) (aⁿ)ⁱ = aⁿⁱ

Rule(5):-

 In case of exponents if any expression has the power of power, then simply powers are multiplied themselves.

(vi)√a = a¹⁽²

Rule(6):-

A surd or root number can be converted into exponent by dividing the power with root value. Let, us now we will prove some above formulas of  exponents.

Prove  that,aⁿ × aⁱ = aⁿ⁺ⁱ

Answer:-

L.H.S = aⁿ × aⁱ   a       =(a.a.a…..n number of factors) × (a.a.a…..i number of factors)          = aⁿ × aⁱ          = aⁿ⁺ⁱ [∵According to law of exponents, if bases are equal then in case of multiplication powers are added]          = R.H.S   Proved.

Prove  that,aⁿ ÷ aⁱ = aⁿ⁻ⁱ

Answer:-

        L.H.S = aⁿ ÷ aⁱ   (a.a.a…..n number of factors) = —-----------------------------------------     (a.a.a…..i number of factors)           aⁿ =  —---------           aⁱ =   aⁿ⁻ⁱ [∵According to law of exponents, if bases are equal then in case of division powers are subtracted]  = R.H.S Proved.

Prove that, a⁰ = 1

Answer:-

           L.H.S = a⁰                       = aⁿ⁻ⁿ                         aⁿ                    = —-------                         aⁿ   [ ∵ Exponents are in subtraction, so they are will be in division individually.]                   =  1                   = R.H.S Proved.

 Prove that, a⁻ⁿ = 1/aⁿ

 Answer:- 

L.H.S = a⁻ⁿ              = a⁰⁻ⁿ                   a⁰              = —--                  aⁿ     [ ∵ Exponents are in subtraction, so they are will be in division individually.]                    1             = —----- [∵using formula(iii)                    aⁿ              = R.H.S Proved.

Some problems related on exponents:

 Express the following numbers in exponents or indices form.

  (i) 64  (ii) 343 Answer:- (i)  64                 = 4³ [∵ 4 × 4 × 4 = 64 ]                = (2²)³ [ ∵ 4 = 2 × 2 ]                = 2⁶ [ ∵ According to the law of exponents power of power is multiplied themselves]           (ii) 343            =  7³ [∵ 7 × 7 × 7 = 343]

Simplify:-

   (i) 125⁻¹⁽³  (ii) 64¹⁽⁶ Answer:-      (i) 125⁻¹⁽³      =  {(5)³}⁻¹⁽³ [ ∵5×5×5 = 125]      = 5 ³×⁻¹⁽³ [ ∵power of power will be multiplied]      = 5⁻¹ [ ∵3×(- ⅓ )= -1]      = ⅕ [ using formula (iv)      (ii) 64¹⁽⁶      = (2⁶)¹⁽⁶      =  2⁶ ×¹⁽⁶ [ ∵power of power will be multiplied]       =  2¹ [∵ 6 ×1/6 =1]       = 2

Find the value of n from the given expression:-

Answer:-   27ⁿ ÷ ⅓  = 3⁵   => (3³)ⁿ ÷ 3⁻¹ = 3⁵    => 3³ⁿ ÷ 3⁻¹ =3⁵[∵using formula(v)] => 3³ⁿ ⁻ ¹ = 3⁵ [∵using formula(ii)]   => 3n - 1 = 5 [ ∵ bases in both sides are equal, so their powers are also equal]   =>3n = 5 + 1   => n = 6/3     => n =2 

 Conclusion:-

From the above discussion we have learnt What are Powers in Math.  Generally exponents ..........

To Read more.......

[champak30]

Title:-  What are ionic compounds?

Introduction:-

What are ionic compounds?is our main discussion today. I am just trying to focuss on the chemistry topic What are ionic compounds?which will be very helpful for class (ix) and class(x) school children, I think.

Explanation:-

To start this discussion, let us first know some basic definitions of chemistry,

what are elements?

Answer:-  The matters which are composed of only one type of particles are known as elements.e.g; Sodium (Na), Magnesium(Mg),  Carbon(C).....

How elements are classified?

Answer:-Elements are classified in three types:-(i) Metals (ii) Non metals. (iii) Metalloids. Metals:- Sodium(Na), Magnesium (Mg), Gold (Au).....  Non metals :-Carbon (C), Sulphur(S),Nitrogen (N)....  Metalloids :- Boron(B), Silicon(Si), Arsenic(As)....

What are molecules?

Answer:- When two or more than two similar or different types of atoms combine together chemically they form molecules  e.g;     H + H —----> H₂      Hydrogen molecule(Diatomic molecule) Cl + Cl —-----> Cl₂

             Chlorine molecule(Diatomic molecule) H₂ + S —------> H₂ S

             Hydrogen sulphide(Triatomic molecule)

What are compounds?

Answer:-    When two or more molecules or atoms chemically  react themselves under some definite conditions and combines then they form compounds. e.g;  C + ½ O₂ —---------> CO (atom) (molecule)  (Carbon monoxide is a gas/compound) C + O₂  —--------> CO₂ (atom) (molecule) (Carbon dioxide is a gas/compound)

Finally I will discuss on todays topic

What are ionic compounds?

Answer:- The compounds which are formed by the transfer electrons from metal atom to non metal atom are known as ionic compounds. e,g; Potassium Chloride (Kcl), Aluminium oxide (Al₂O₃) Now we will learn a little more on ionic compounds .

How following ionic compounds are formed?

(a) Sodium Chloride (Nacl)

Answer:-  Na is a metal, the electronic configuration of sodium (Na) = 2,8, 1  to complete octet and become stable sodium needs to collect 7 electrons from other element to full fill its outer most shell i.e its third shell or 'M' shell to get its nearest noble gas Argon (2,8,8) and to full fil octet and become stable or Na has to give up its only valence shell electron (1) to get 2,8 electronic configuration of Neon as sodium is a metal so according to metals chemical property , all metals give up electrons they do not accept electrons or they are unable to accept electrons due to strong inter molecular force, thats why sodium is also unable to accept 7 electrons.

Again, chlorine (Cl) is a non metal and its electronic configuration is 2,8,7 so to fulfil its octet chlorine needs to accept one(1)electron or must have to give up its valence shell's 7 electrons  to get either its nearest noble 2,8,8(Argon) or 2,8 (Neon) gas configuration  to become stable due to non metals chemical property non metals never give up electrons, so chlorin is also unable to give up electrons.So in chemical reaction between sodium(Na) and chlorine ,Sodium (Na) gives up its lone valence electron to get its nearest noble gas Neon's configuration(2,8) and become stable in the mean time chlorine accepts the lone electron which is given up by sodium(Na) to get its nearest noble gas Argon's (2,8,8)configuration and become stable and by the process of electrons transfer they form ionic compound (Nacl) The formation can be given by:-

(b) Magnesium Oxide (MgO)

Answer:-  Magnesium is a metal,the electronic configuration magnesium(Mg) is 2,8,2  and these electrons occupies s,p,and d orbits. To become stable or get its nearest noble gas ,argon's(Ar) configuration(2,8,8) magnesium need 6 more electrons to fill up its d-orbit and to become stable but due to inter molecular force of electronic attraction magnesium is unable to take 6 more electrons from other atoms.       On the other hand oxygen is a non metal and electronic configuration of oxygen is 2,6 ; which occupies its s and p orbits.To get its nearest noble gas, Neon's electronic configuration (2,8)oxygen need 2 more electrons  to fill up its p-orbit and to get (2,8) neon gas configuration and to become stable.    So  in the chemical reaction between magnesium and oxygen one magnesium(Mg) atom gives up its lone pair(2) electrons to get neons configuration(2,8) and become stable also produces Mg⁺² ion ,in the same time one oxygen  atom accepts 2 electrons which are given up by magnesium (Mg) aton also to get its nearest noble gas  neon gas configuration (2,8) and become stable also produces o²⁻ion. Due to electro atomic force of attraction between Mg⁺² ion and o²⁻ion they combines themselves and produces magnesium oxide (MgO)   The formation can be given by :-    Mg  - 2e —-------> Mg⁺² (Magnesium ion)  (2,8,2)                     (2,8) neon gas    O  + 2e —-------> O²⁻(Oxygen ion)   (2,6)                    (2,8) neon gas Now    Mg⁺² + O²⁻ —------>Mg⁺²O²⁻ —->MgO

(magnesium oxide)

(c) Potassium Oxide (K₂O)

Answer:-  Potassium is a metal,the electronic configuration magnesium(K) is 2,8,8,1  and these electrons occupies s,p, d and f orbit. To become stable or get its nearest noble gas ,krypton's(kr) configuration(2,8,8,18) potassium need 17 more electrons to fill up its f-orbit and to become stable but due to inter molecular force of electronic attraction magnesium is unable to take 17 more electrons from other atoms.        On the other hand oxygen is a non metal and electronic configuration of oxygen is 2,6 ; which occupies its s and p orbits.To get its nearest noble gas, Neon's electronic configuration (2,8)oxygen need 2 more electrons  to fill up its s-orbit and to get (2,8) neon gas configuration and to become stable.     So  in the chemical reaction between potassium and oxygen two potassium(K) atom gives up its lone (1) electron each to get argons configuration(2,8,8) and become stable also produces K⁺ ion ,in the same time one oxygen  atom accepts 2 electrons which are given up by two potassium (K) aton also to get its nearest noble gas  neon gas configuration (2,8) and become stable also produces o²⁻ion. Due to electro atomic force of attraction between 2K⁺ ion and o²⁻ion they combines themselves and produces potassium oxide (K₂O)   The formation can be given by :-

Conclusion:-

 Ionic compounds are formed by the transfer of electrons from metal atom to non metal atom......

To read more....

[champak30]

This is a science story.To read please visit my profile https://www.instagram.com/p/Cop4Zk4S3lt/?igshid=NGJjMDIxMWI=