geometricloci

[geometricloci]

[geometricloci]

pentagon dance

[geometricloci]

[geometricloci]

What is Group Theory?

In math, a group is a particular collection of elements. That might be a set of integers, the face of a Rubik’s cube–which we’ll simplify to a 2x2 square for now– or anything, so long as they follow 4 specific rules, or axioms.

Axiom 1: All group operations must be closed, or restricted, to only group elements. So in our square, for any operation you do—like turn it one way or the other—you’ll still wind up with an element of the group. Or for integers, if we add 3 and 2, that gives us 1—4 and 5 aren’t members of the group, so we roll around back to 0, similar to how 2 hours past 11 is 1 o’clock.

Axiom 2: If we regroup the order of the elements in an operation, we get the same result. In other words, if we turn our square right two times, then right once, that’s the same as once, then twice. Or for numbers, 1 + 2 is the same as 2 + 1.

Axiom 3: For every operation, there’s an element of our ground called the identity. When we apply it to any other element in our group, we still get that element. So for both turning the square and adding integers, our identity here is 0. Not very exciting.

Axiom 4:  Every group element has an element called its inverse, also in the group. When the two are brought together using group’s addition operation, they result in the identity element, 0. So they can be thought of as cancelling each other out. Here 3 and 1 are each other’s inverses, while 2 and 0 are their own worst enemies.

So that’s all well and good, but what’s the point of any of it? Well, when we get beyond these basic rules, some interesting properties emerge. For example, let’s expand our square back into a full-fledged Rubik’s cube. This is still a group that satisfies all of our axioms, though now with considerably more elements, and more operations—we can turn each row and column of each face.

Each position is called a permutation, and the more elements a group has, the more possible permutations there are. A Rubik’s cube has more than 43 quintillion permutations, so trying to solve it randomly isn’t going to work so well. However, using group theory we can analyze the cube and determine a sequence of permutations that will result in a solution. And, in fact, that’s exactly what most solvers do, even using a group theory notation indicating turns.

From the TED-Ed Lesson Group theory 101: How to play a Rubik’s Cube like a piano - Michael Staff

Animation by Shixie

[geometricloci]

There’s always space for another proof of Pythagoras.

[geometricloci]

This world is known as the group of integers modulo 3, commonly referred to as “Z3″. In this place the only numbers are 0, 1 and 2. The diagram above shows how addition works in a loop. In Z3 1 + 1 is still 2 but things get a little strange when we add with 2s, for example 2 + 1 = 0 and 2 + 2 =4.

Some may think, “Okay, but is this really real?” or “Is this even useful?” Well, you should already be used to a world where things like 9 + 5 = 2 and 12 + 6 = 6. The world of hours on a clock! We use that kind of math all the time and it makes enough sense. (BTW, clock hours have the same structure as the group of integers modulo 12 aka Z12).

[geometricloci]

Brief animation of next pattern set - ‘Smaller and smaller’

[geometricloci]

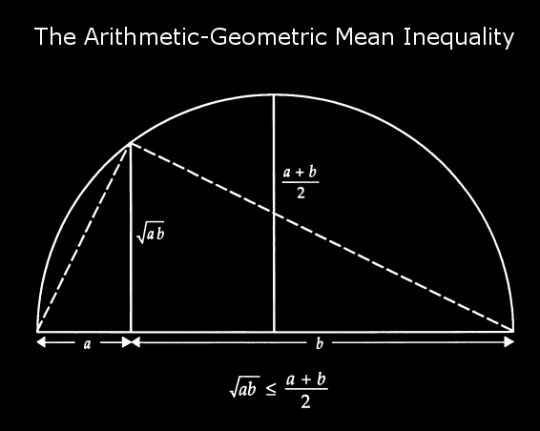
From “Proofs Without Words” by Roger Nelsen. 

[geometricloci]

A level further mathematics question animated.  Mid point of Normal x-intercept and Tangent y-intercept traces out another curve as original point moves round an ellipse.

[geometricloci]

Today is very special day (in a relative way) because it’s both Super Pi Day and Einstein’s birthday! Make sure to celebrate by stopping and thinking about how you have mass and thus gravitationally influence the world around you. This means that you, simply by merit of your existence, are able to warp the fabric of spacetime itself. And even better, gravity is asymptotic, so all that warping and tugging you’re doing will go on forever and ever—emanating from you at 671,000,000 miles per hour and making a permanent impression on the cosmos! Eventually your gravity will extend out past our galaxy and influence (even if only by the slightest amounts) stars and planets and nebulae that are millions and billions of lightyears away! 

Yay!

Happy Einstein and Pi Day!

[Photo credit]

[geometricloci]

Fonte

[geometricloci]

the hype: light version

[geometricloci]

My Math Art :-)

[geometricloci]

Orbit trap fractal, female

[geometricloci]

MathGV software

[geometricloci]

Enlargement.

[geometricloci]

Ancient theorem of Euclid (Book III, Proposition 31) still a fundamental part of school maths.  The angle in a semi-circle is a right angle.