gilliansmb

[gilliansmb]

Blog Entry # 29: Extrema, Concavity, and Sketching Graphs using Derivatives

These last 3 weeks, we talked about the Extrema and first derivative test, concavity and the second derivative test, and sketching a graph using derivatives. Since these three topics are closely related to each other, I decided to merge these in one blog entry.

This topic was easily digestible, given the specific steps needed to form a mental and physical image of the graphs discussed. Topics from the past quarters are now recognizable in this topic, which makes me feel a sense of fulfillment for remembering those topics for the rest of the school year.

Nonetheless, I practiced forming tables using the first and second derivative tests.

This set took me a few minutes to understand since it was already discussed during the synchronous meeting.

In conclusion, these topics have really helped me in visualizing graphs of certain equations just by some calculations. Hopefully I can use all these topics in the future for real-life application.

That would be all from me! Thank you very much for staying with me throughout this entire school year! Happy summer break! 🫶

[gilliansmb]

Blog Entry # 28: Related Rates

This week, we talked about related rates.

So far, among all the lessons we’ve tackled for the entire school year, I’ve never been as hard up in understanding a topic as I’ve been this week. After hours and hours of searching for practice problems, watching tutorials on Youtube, and rereading learning guides, I still had no idea what I’ve been doing on my scrap paper.

Although I’ve been having trouble in understanding the lesson, I still tried to understand some problems. Some of them were a bit easier to digest compared to others, like the problem shown below.

This problem took me around 20 to 30 minutes to understand and solve.

In conclusion, this was one of the topics I had trouble understanding. Allotting more time to topics like these is a must. As for my expectations for next week’s topic, I just hope that I would be able to allot more time in understanding the topic.

That’s it from me for this week! See you in the next!

[gilliansmb]

Blog Entry # 27: Rates of Change and Rectilinear Motion

This week, we talked about rates of change and rectilinear motion.

This topic was a topic I enjoyed learning about, ans was more enjoyable to me compared to last week’s topic. Although the title of the topic seemed intimidating at first, the synchronous meeting made me realize how simple and easy to understand it really is.

Nonetheless, I answered some problems from the practice quiz and other online sources.

It took me about a 10 minutes to answer the practice quiz.

In conclusion, this topic has been fun in my opinion, and I hope that the future topics would have the same difficulty as this one.

That’s it from me for this week! See you in the next!

[gilliansmb]

Blog Entry # 26: Optimization

This week, we learned all about optimization.

As I always stated, I am really bad at word problems. Since I was in elementary, I could never get into both the process of solving these types of questions, so when I learned that for this week, we would be tackling optimization, I was internally panicking.

Nonetheless, I started solving some practice problems. This is a problem from the interactive lesson that I solved. I was really confused throughout the whole duration of the interactive lesson but maybe it was because I was answering and listening at 10 pm, a time when I am usually already fast asleep.

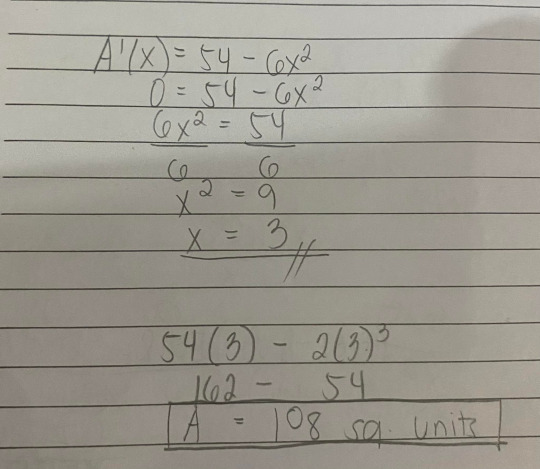
Solving this took me about 20 minutes to understand and solve.

In conclusion, this was a rough start to the final quarter of the school year. I really thought I’d use this chance to make up for my performance last quarter, but I guess things really don’t always turn out the way you want them to. In the bright side, there are still plenty more topics in this quarter, meaning more chances for me to break through this unlucky and unproductive streak. I’m hoping that these lessons will help me improve some more skills I really don’t like facing like how this topic made me face my fear and hostility towards problem solving and word problems.  

That’s it from me for this week! See you in the next!

[gilliansmb]

Blog Entry # 25: Long test 3-2

*sigh* here it is, last long test na.

After postponing taking the long test multiple times, I finally gathered the courage to make an attemp yesterday, March 31st, at around 11 pm.

As usual, the long test was made up of two test types: multiple choice and extended response. I found the multiple choice questions less challenging than the extended response questions, but that is just because I have choices to choose from.

This time however, my lack of sleep has taken a toll on me and has made me submit the same picture for both extended response questions, which I later cleared up with Sir Jed (I also forgot to schedule the email, so I hope I didn’t wake sir up 😭). Nevertheless, I found this long test’s set of extended response questions less time consuming compared to the first long test’s.

In conclusion, similar to my conclusion in the last long test, you shouldn’t take or do mahor requirements when you’re lutang or sleep-deprived. Also, hopefully in the last quarter of the school year, I’ll take these little tips I have for myself from the conclusion part of my blogs to make the most of the final quarter.

That’s it from me for this quarter! See you in the next!

#MakakatulogNaNangMahimbingSaGabiNangWalangReqsNaIniisip #CharotLang

[gilliansmb]

Blog Entry # 24: Higher Order Derivatives

This week’s topic was a very memorable one because of two things: the introduction video Sir Jed made, and the level of complexity of the topic.

For one, I am very used to doing my requirements at night when my brain works at about 40-50%. When I watched the introduction video Sir Jed made, it really made me burst out laughing and increased my brain’s learning power. Not only was the vid funny, but it was also very informative as it gave me the basic information about the topic, examples, and real life applications. I hope there are more of these in the future hehe.

Aside from the introduction video, the level of complexity of the topic also caught me off guard, since I was expecting a topic that was harder than the previous topic, which I found challenging.

Anyways, here is a picture of solutions from practice problems:

I got these from when I was answering the practice quiz, which I surprisingly got full credits for despite being half-asleep at the time.

In conclusion, I had fun solving and learning about this topic, and I this is a good way to end the quarter. Hopefully, I retain all the knowledge I have gained this week in order to apply them to the upcoming long test.

That’s it from me for this week! See you in the next!

[gilliansmb]

Blog Entry # 23: Implicit Differentiation

This week, we talked about implicit differentiation.

This topic was confusing to me at first. I didn’t understand much from the synchronous class, so I decided to focus more on sample problems exercises.

Speaking of, here are some solutions from sample problems I tried:

If I recall correctly, these are some questions I got wrong from the practice quiz. Like usual, understanding the lesson took more time than actually solving the problems.

In the end, I fully understood the lesson but I wish I still had more time to master and practice my skills on this topic. Requirements are starting to oile up this week and hopefully I can get more practice after I cram my requirements.

That’s all from me for this week! See you in the next!

[gilliansmb]

Blog Entry # 22: Long Test 3-1

This quarter’s first long test was a roller coaster for me. From what I recall, there were two parts of the LT: multiple choice and extended response (or problems which required solutions.

Personally, the multiple choice questions weren’t as tedious compared to the extended response questions. Out of the amount of time it took me to finish the LT, I have spent most of it on the latter part of the LT since writing the long solutions to the problems were very time consuming, and I also wasn’t even sure of what I was writing most of the time.

Since I do not have any pictures of solutions for this week, here’s a song I listened to for the whole duration of the long test: 

In conclusion, don’t take or do serious requirements when you’re lutang (joke). I hope that this will serve as a lesson for me and that these small inconveniences like running out of paper or motivation to solve the problem will help me improve, specially in the next long test, so I won’t feel like I’m only moving backwards.

Anyways, that’s it from me for this week! See you in the next!

[gilliansmb]

Blog Entry # 21: Chain Rule

This week, we learned all about the Chain Rule.

This lesson was looked really easy when I was listening during the synchronous meeting, but when I got to solving some practice questions, I got really confused as to what I was doing, specially with the combination of transcendental functions and trigonometric functions. 

Nonetheless, here are some sample solutions I had from exercise questions:

These took me a while to get a hang of, but after a few practice problems, solving these got easier eventually.

In conclusion, I learned to never judge a lesson by how easy Sir Jed makes it out to be (joke). I hope that the next lesson will involve more applications of the chain rule that will help me improve my mastery on the subject.

That’s it for this week! See you in the next!

[gilliansmb]

Blog Entry # 20: Derivatives of Transcendental Functions

This week, we talked about the derivatives of transcendental functions.

During the synchronous class, I noticed that this lesson was really similar to last week’s lesson, just a bit harder. In the first place, I have really bad memory so recalling the transcendental functions took me a while before getting practice questions on this week’s topic right.

Anyways, here’s a picture of solutions to exercises in the practice quiz:

I got these questions wrong on the practice quiz, so after a bit more thinking, I finally got the final answer displayed on the quiz.

In conclusion, I really should keep a notebook with important formulas so that I won’t have a hard time recalling next time we have lessons like this. Nonetheless, I found this topic really interesting since not only did it made me recall a lesson I had already forgotten about, but it also increased my knowledge and mastery on solving these kinds of problems.

That’s it from me for this week! See you in the next!

[gilliansmb]

Blog Entry # 19: Rules of Differentiation

This week, we talked about the rules of differentiation.

At first, I thought this was where things were about to go downhill and I would understand the lesson less than I did last week, but it turns out I was wrong. During the weekly synchronous meeting, I was surprised to learn that this week’s topic was more of a way to enhance our skills on last week’s topic, or at least lessen the time we take to solve derivative problems. 

Nonetheless, I tried some practice problems from the link posted on our KHub course.

These two problems pretty much took less than 10 minutes to solve. Understanding the lesson was the part that took me longest.

In conclusion, I think that this lesson would become a basis to much more harder topics in the future, similar to past topics like Limit Theorems. I will be looking forward to how I can apply the knowledge I have gained in this lesson to other, more complex lessons.

That’s it from me for this week! See you in the next \(^_^)/

[gilliansmb]

Blog Entry # 18: The Tangent Line and the Derivative of a Function

This week, we discussed tangent lines and derivatives of functions.

A few days before the start of the 3rd quarter, I decided to scan through the learning guides just so I can get an idea of what to expect for this week’s topic. When I first saw that we were going to be studying tangents, I am reminded of a meme I previously saw on Reddit:

Anyways, since we already have talked about tangents in our previous years, I thought that the topic would involve more graphing than solving. As for derivatives, I have seen the term online for when I was looking up videos about limits before the previous quarter exams, but I didn’t quite understand how it was used and the use of dy/dx made the topic even more intimidating, so I never bothered to read more about it.

During the weekly synchronous class, I noticed that this is where my skills on limits came in handy. As I was studying the interactive lesson, I felt thankful to my past self for listening to and taking notes during class as it all became helpful in the end.

Nonetheless, here are some practice solutions to problems in the interactive lesson:

This set took me about 20 minutes to solve, since it was the first two questions I have encountered about the topic.

In conclusion, this topic was more of a recall for the majority of last quarter’s topics, making this topic a great way to start the quarter. Hopefully, the following weeks will go as smoothly as this week did, and I hope that I will get to apply everything I have just learned not only in the past quarters, but also in the past grade levels.

That’s it from me for this week! See you in the next !!

[gilliansmb]

Blog Entry # 17: Continuity and Discontinuity of Functions at a Number

This week, we discussed the continuity and discontinuity of functions at a number.

These past few weeks have been the most challenging weeks for me in this subject, but this topic has given me hope a tiny bit of hope since I found it a bit easier to understand compared to the previous topics. Not only that, but also this week’s topic featured an interactive lesson (which I have truly missed).

Another thing I love about the topic is that it does not feature much solving, and its concept is easier to grasp, since the topic features a set of requirements to fulfill to be able to label a certain function as continuous or discontinuous.

Anyways, here is a sample problem found in the practice quiz:

What type of discontinuity the function is exhibiting is being asked. This function exhibits removable discontinuity since its functional value at x = 2 does not exist, as shown below: 

Overall, I found this topic very interesting since it isn’t a typical math problem wherein we have to find a definite answer, but instead we have to provide proof that a certain function is continuous or discontinuous.

Also, this whole quarter has been a rollercoaster with its own ups and downs. I have experienced so many emotions as I journeyed through all of the weekly topics. Although I think I did pretty badly, I think we all deserve a pat on the back just because we ‘survived’ all the obstacles and problems life has given us. 

Although some problems may arise and make us reach our own limits, we will find infinite possibilities to stay positive, survive, and thrive (≧∇≦)ﾉ

That’s it from me for this quarter! See you after a week!

[gilliansmb]

Blog Entry # 16: Limits on Trigonometric Functions

This week, we talked about limits on trigonometric functions, which is a continuation of last week’s topic.

When this topic was introduced, I felt a bit uneasy because when during the synchronous meeting, the solutions to the problems were a bit more complex compared to the limits on logarithmic functions, which took me a long while to understand. 

When I was studying the topic by myself however, it reminded me a little of the squeeze theorem, since trigonometric functions were also presented in that topic.

Anyways, I attempted to solve some sample problems found in the learning guides and various sources online.

This problem took me about 20 minutes to solve and rewrite, but understanding the topic took me more than an hour, though I am still a bit careless with my skills.

Similar to last week, I think this topic has been an eye-opener to me since I have completely forgotten some, if not most, of the topics during my previous years. Anyways, I look forward to honing my skills with more practice problems and discussions with my friends in the following weeks.

That’s it for this week! See you in the next!

[gilliansmb]

Blog Entry # 15: Limits on Exponential and Logarithmic Functions

This week, we talked about limits on exponential and logarithmic functions.

When this topic was introduced to us during the first synchronous class of the week, I have mixed emotions. At first, I thought this was going to be a bit easy for me because it is a combination of a topic that just had been introduced to us this year and a topic that we have heard before in our past math classes, but then it suddenly hit me that I forgot almost all of my knowledge, which means I would need to re-learn all of the basics again.

Anyways, since there was no interactive lesson this week (which I am a huge fan of, if you haven’t noticed in my previous blogs), I had to do it the hard way, by reading the modules, looking up videos about it online, and referring to the book for sample problems. Nonetheless, shown below is a solution to some practice problems.

The first two practice problems shown below were from the internet, while the last one was from the learning guide. All in all, these took me about 30 minutes to answer, and an hour to understand.

In conclusion, I think this topic has made me realize my shortcomings in math, since I had to watch more videos on logarithmic functions just to understand the topic, when I could have just took note of it in my previous years. Nonetheless, this lesson has been a challenge for me since not only is it testing my abilities in problem-solving, but also my ability to study through other mediums and not only relying on the interactive lessons.

That’s it for this week! See you in the next!

[gilliansmb]

Blog Entry # 14: Squeeze Theorem and Longtest 1

This week, we glossed through squeeze theorem, and focused on the first longtest of the quarter.

Although we did not have an in-depth discussion on squeeze theorem this week, I will be focusing on my thoughts for this topic in this reflection since this will serve as a review for the upcoming second longtest for the quarter.

In my understanding, squeeze theorem just states that if the value of g(x) is between f(x) and h(x) near a, and f(x) and h(x) have the same limit L at a, then the limit of g(x) is forced to be equal to L to make the inequality correct.

This topic somehow reminds me of limits of piecewise-defined functions, since both show inequalities. 

Anyways, I found some sample problems to practice my skills and understanding on the topic:

This is a sample problem involving trigonometric functions, specifically involving a sine function. This took me about 10-15 minutes to understand, since this was the first sample problem I attempted to solve.

This next sample problem involved a cosine function. Answering this problem took me about 5 minutes, much les compared to the first problem since both had a similar process of solving.

Overall, I found the topic really intimidating at first, but once I got to grasp the main idea of the topic, answering some problems became easier for me. I hope to apply this knowledge in the following weeks’ topics. 

That’s it for this week! See you in the next!

[gilliansmb]

Blog Entry # 13: Limits at Infinity

This week, we talked about limits at infinity.

Similar to last week’s topic, I found this topic interesting since it involves the boundless possibilities of a certain question (waw deep pt. 2 XD), which again says a lot about our human nature.

Anyways, here is a picture of my solutions to some practice problems from the interactive quiz:

If I recall correctly, this set took me less than 15 minutes to solve.

In conclusion, I found this week’s topic interesting because similar to last week’s topic, it was easy to digest and understand using the different given materials such as the learning guides, interactive lesson, and practice quiz.

That’s it! See you in the next!