language-of-math-blog

[language-of-math-blog]

Discontinuity

I’m working through the MITx calculus course on differentiation, and I’m getting stuck on the concept of discontinuities.

I see all these breaks and holes and jumps in the graphs, but I just couldn’t wrap my head around what it meant. What kind of real-life phenomenon was this graph modeling? How could I apply this concept in real life?

I took to Google for an answer, and was happy to say I found one in short order :)

Math Captain explains discontinuities very simply and intuitively:

In real life discontinuity is experienced in the form of breaks and abrupt changes. Mathematically a function is said to be discontinuous when the graph of the function contains breaks and jumps. (Source)

I was so happy he defined it as an “abrupt change”—that helped me retain my understanding of the notion that calculus is about change.

I also came across a wonderful real-world application of discontinuous functions by user soroban over on FreeMathHelp.com (Source). There, soroban states:

Suppose a delivery service (UPS, FedEx, etc.) charges, say, $5 per pound. The rates are usually given as: “Five dollars per pound or fraction thereof.” This means that they will always “round up.”

So if your package weighs 1 lb, you pay $5. If it weighs 1 lb 1 oz., you pay $10 because 1 oz is a fractional proportion of the second pound. Even though it’s just slightly over 1 lb, it is over, and so the price abruptly changes—jumping from 5 bucks to 10!

The graph becomes a step function, specifically, the ceiling function as soroban write in the post:

     |  $20 |                 o-----*      |  $15 |           o-----*      |  $10 |     o-----*      |-   $5 o-----*      |    - + - - * - - * - - * - - * - - -      |     1     2     3     4  (lbs.)

As soroban summarizes:

The function has jump discontinuities at every integer value.

This was a perfect explanation and I’m so happy to have stumbled across it. I think I’ll be able to easily move forward with this review of limits with the understanding that the discontinuities, jumps and holes in the graph represent points of abrupt change.

[language-of-math-blog]

-source @michelerosenthal

ARTISTSFOREDUCATION

[language-of-math-blog]

Multiples

So I’m working through this course on edX to prepare myself for the Calculus courses I’ll be taking soon, and for some strange reason, I cannot get the concept of multiples through my head.

Factors I understand, and I thought that understanding multiples as the inverse of factors would help me get it, but that seems to have just confused me even more.

So I’ll try to see if I can’t understand it better through words.

Math Is Fun tells me that a multiple is

The result of multiplying a number by an integer (not by a fraction).

I think it’s important for me to focus on that bold word: result.

So, if I ask, what are the multiples of 3? Then I multiply 3 by any number of integers, for example:

3 x 2 = 6 

3 x 4 = 12

3 x 7 = 21

And 6, 12 and 21 are multiples of three because these are the numbers I get when I multiply three by various integers.

That did it!!

When I went back to try the problems on the maths course again, I reworded the question from this:

18 is a multiple of which of the following numbers?

to this:

18 is a result of which of the following numbers?

I was able to answer all of the questions right, because I had a better understanding of what the question was asking of me.

Excited to keep moving forward!

[language-of-math-blog]

Discriminants

I have NO idea what a discriminant is. I’ve been skipping these questions on Khan Academy because I just have absolutely no clue what to solve for. So let’s see if we can shed some light on this.

Speaking of Khan, he tells us what discriminants are in this article:

The discriminant is the part of the quadratic formula underneath the square root symbol: b²-4ac. The discriminant tells us whether there are two solutions, one solution, or no solutions.

In other words, the discriminant tells us if and where the function touches or crosses the x-axis.

(Image source)

Pat Ballew gives a similar explanation:

discriminant To most algebra students the discriminant is a number related to a quadratic equation that determines the nature of the solutions. The value of the discriminant in a quadratic is given by the expression B2 - 4AC. A positive discriminant indicates two real distinct roots, a zero indicates a single real root, and a negative value indicates two complex roots. The actual polynomial discriminant has a denominator which is a power of the leading coefficient, but as the most common use is to determine the number of roots, the (always positive) denominator is ignored. (Source)

However, Ballew also expands on the origins of the word discriminant itself:

The origin of the word is from the union of dis, and the very early Indo-European root skeri which referred to separating by sifting, scraping or cutting, through the Greek krinein to separate. Descendants of the skeri root show up in diverse words today including script, crime, decree, secret, and endocrine.

In other words, the “discriminant” of a function helps us to “separate” out the solutions. But this etymology is a bit difficult to understand. Through Google we can trace the true etymology and find some friends in the process:

discriminant 19th century (in the sense ‘showing discernment’): from Latin discriminant- ‘distinguishing between,’ from the verb discriminare (see discriminate).

discriminate early 17th century: from Latin discriminat- ‘distinguished between,’ from the verb discriminare, from discrimen ‘distinction,’ from the verb discernere (see discern).

discern late Middle English: via Old French from Latin discernere, from dis- ‘apart’ + cernere ‘to separate.’

I like this flow better. The discriminant is the part of the quadratic formula that helps us to discern the number of solutions for a given equation.

Now I know!

[language-of-math-blog]

“Hypotenuse”

Hypotenuse comes from the common Greek root hypo(for under, as in hypodermic -under the skin) and the less common tein or ten, for stretch. This last is the source of our modern word tension. The hypotenuse was the line segment "stretched under" the right angle. (Source)

Okay, I’m totally confused by this. How can the hypotenuse be “stretched under” the right angle? Maybe I’m just not visualizing things correctly. Perhaps an image will help?

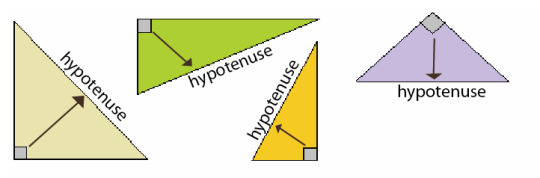
(Image courtesy of Mathspace)

Alright, this is the first image I found that makes it clear that the hypotenuse can, in fact, be “stretched under” the right angle. I guess I’m just so used to see it on the side, with the right angle touching the “floor,” that I didn’t realize what other configurations could be valid.

That purple triangle in particular makes it very clear where this word originates from!

[language-of-math-blog]

Bowls

I just learned something amazing: “parabola” shares the same root word as “hyperbole.” Here’s how it breaks down (quotes from this source):

The word parabola literally translates "to throw beside". The Greek root bole, which is the ancestor of ball, bowl, bubble, and many such words today was closer to throw or place in the Greek usage.

Parabolas do kind of look like bowls, don’t they? In fact, in machine learning one of the ways I was taught to understand gradient descent was to think of it as a bowl that we’re trying to find the bottom of.

Pat Ballew goes on to say:

Para is a root for beside, as we see it in parallel. Parallel refers to two lines that are "beside" each other. Think of a parabola as the shape obtained when the cutting plane is "thrown" alongside the slope of the cone. A closely related word is parable, a story that is not true, but true-like, or "thrown beside" the truth. The parathyroids are so named because they are beside the thyroids.

This explanation requires an understanding of conic sections, which I got pretty quickly after looking at this image from Wikipedia:

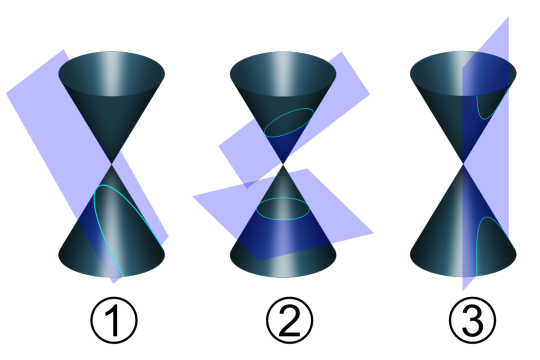
where (1) shows a parabola, (2) shows an ellipse and a circle, and (3) shows hyperbolas. I’m sure I’ve seen hyperbolas before (and after googling images of them on a graph I do, indeed, remember having seen them before) but this is the first time I was able to truly understand it.

Anyway, back to parabolas. They are the shape that we get when a cutting plane is, as Pat Ballew says, “‘thrown’ alongside” the slope of the cone.

Since we’ve got that image up there, let’s go ahead and see what Ballew says about the origins of the other conic sections:

Ellipse

The ellipse is a shape formed when the cutting plane of a cone falls short of the slope of the cone, and the meaning, as you expected, is to fall short. The use of three dots or asterisks to mark where part of a statement has been left out is called an ellipsis for the same reason.

Wikipedia notes that the circle in image 2 is a special form of an ellipse, and that many consider it to be a fourth conic section in its own right.

Hyperbola

The hyperbola shares the common bola root, but this time the throw is "more than enough" or beyond the slope of the cone, creating a hyperbola. Hyper as more than enough or an overabundance appears in the names of objects with more than three dimensions, and the fourth dimension equivalent of a cube is called a hypercube. Hypertension means too tense. The opposite of hyper is hypo, as in hypodermic, which translates to "under the skin", and of course, Hypotenuse.

The English term, hyperbole derives from the same root words as hyperbola, and is used for an obvious exaggeration or extension of the truth.

Didn’t know that about the hypotenuse! Think I’ll go check that one out next ;)

[language-of-math-blog]

“Quadratic”

QUADRATIC is derived from the Latin quadratus, meaning "square." In English, quadratic was used in 1668 by John Wilkins (1614-1672) in An essay towards a real character, and a philosophical language[London: Printed for Sa. Gellibrand, and for John Martyn, 1668]. He wrote: "Those Algebraical notions of Absolute, Lineary, Quadratic, Cubic" (OED2) (Source)

Quadratic is the Latin root for "to make square". The word square was itself derived from this root (Source)

Square is derived from the Latin phrase Exquadrare, like a quadratic. Over time the term was contracted into its present form, and came to mean the regular quadrilateral. The word is also the root of the military term squadron, which originally meant a fighting square from the early practice of fighting in square formations. (Source)

Apparently some people call squares “quadrangles,” to match with triangles, and others call them “tetragons” to match with pentagon, hexagon, octagon, etc. I would have much preferred these uses to “square” which never seemed to fit in with the other shapes (i.e. triangle, rectangle).

[language-of-math-blog]

e

This number is something I’ve never understood.

However, after watching this video I’ve got a better grasp at the situations where it’s used:

to calculate compound interest

to describe the normal distribution

to model populations

to describe exponential decay

If you increase the number of compounding periods a year, towards infinity, then you’ll get closer and closer to e dollars. (Source)

The common log allows us to talk in multiples of 10. So what does the natural log (the base e) allow us to do?

According to this source, e is referred to as a “magical number.” I agree with that! It’s also called “Euler’s number” and the “irrational constant.” Regardless, e is fundamental to growth in nature.

Here is the definition that video gives for e:

The maximum possible result after continuously compounding 100% growth over one time period.

But Better Explained tells us that we can’t simply focus on this. We have to extrapolate out to the intuition behind the number:

e is the base rate of growth shared by all continually growing processes. [It] lets you take a simple growth rate (where all change happens at the end of the year) and find the impact of compound, continuous growth, where every nanosecond (or faster) you are growing just a little bit.

Pat Ballew tells us that a compound number is a number with a whole part and a fractional part put together, i.e. 1 + 1/n. This is exactly what it means to compound in the case of interest, as we add a fraction (the interest) to our principal (the whole).

If you compound at certain discrete time intervals, then I don’t think you’ll approach e. This seems to only happen when a system is growing both exponentially and continuously, that is, over an infinite number of time periods.

Better Explained sums it up as follows:

Just like every number can be considered a scaled version of 1 (the base unit), every circle can be considered a scaled version of the unit circle (radius 1), and every rate of growth can be considered a scaled version of e (unit growth, perfectly compounded).So e is not an obscure, seemingly random number. e represents the idea that all continually growing systems are scaled versions of a common rate.

I still don’t think I’ve understood it perfectly, but these explanations are a good start.

[language-of-math-blog]

Exponents, Radical and Logarithms

I’ve just finished a series of short posts that goes into the etymology behind these terms, and now I’d like to take a quick look at the history and use cases for these operations.

Exponentiation

The term “exponent” was first seen in the 16th century, in a work titled Arithmetica Integra (1544) written by Michael Stifel.

But the concept of squaring numbers and raising them to higher powers goes back much farther than that:

The earliest known symbols to indicate the power of a number appear in ancient Babylon and Egypt. It seems the Babylonians had ideographs for both squaring and cubing a value. In an Egyptian papyrus now in Moscow, a symbol, which looks like a drawing of a pair of walking legs, is used to indicate multiplying a value by itself. (Source)

Exponents are simply shorthand for the operation of multiplying a value by itself. Instead of writing 6x6x6x6x6x6x6x6x6x6, you can just write 6^10.

The shorthand for exponentiation has changed over the centuries, until arriving at our modern-day usage.

Here are some examples of exponentiation in real life (Source):

1. Measurement. More specifically, area and volume. A square foot is the area of a square whose sides are equal to 1 foot. Area is lengthxwidth, and if all the sides are the same we get 2x2 which is 2^2. Similarly, a cubic meter measures the volume of a cube with sides that are equal to 1 meter. Since a cube has three sides, we get 3x3x3 which is 3^3. I also like how the 2-dimensional measurement is squared, and the 3-dimensional measurement is cubed.

2. Bits and bytes. Computers are based on binary architecture, and multiples are expressed in powers of 2. Thus we have 32-bit and 64-bit computers, download speeds that jump from 128kbps to 256kbps, and so on and so forth. 

3. Growth. Exponential growth is a crucial component of demographics (i.e. the rate at which a population grows), computing (i.e. the rate at which the speed and power of computers increases), finance (i.e. the rate at which money invested earns interest on the interest), biology (i.e. the rate at which diseases spread) and other natural sciences (i.e. the rate at which radioactivity decays).

Radicals

The radical is another shorthand notation. It is the symbol by which we acknowledge that the radicand (the number underneath the repeat bar) represents a value that has been multiplied by itself a given number of times (root).

Finding the root of a power can be a complicated process, as the answer frequently requires decimal notation. But why would we need to find the root number in the first place? When would we ever use this?

1. Construction. Builders may need to perform a “diagonal check” on the building to ensure that the final structure will hold the desired shape. They wouldn’t be able to perform this check without knowledge of square roots. (Source)

2. Finding outliers. The normal distribution is used all over the place to analyze populations and the distribution of variables throughout that population. If you’re interested in finding “abnormal” or anomalous values, then you’ll need to know square roots, as the equations for finding these values use this operation. (Source)

3. Measurement. Since finding the root is the inverse of exponentiation, we can reverse our area measurement to find the dimensions of, say, an apartment. If you know the total area is 400 sq ft, then you can use the square root to figure out that the apartment is 20 ft x 20 ft (Source). You also need square rooting to find distance, especially when using the formula derived from the Pythagorean theorem.

Logarithms

Remember, the logarithm is the number to which a base is raised to get the power. We use the base and the power to find the exponent.

There is a basic logarithm called the “common logarithm” that is understood to operate on base 10. From what I understand, this operation was used to reduce the amount of time needed to perform calculations in science and engineering, for instance. 

Here’s an example (from Source):

Historically, logarithms are interesting because they allow you to use addition to do multiplications.  For example, if you want to multiply 365.49 by 1474.3, you can do this:         x = 365.49 * 1474.3    log  (x) = log  (365.49 * 1474.3)     10         10  log  (x) = log  (365.49) + log  (1474.3)     10         10              10  log  (x) = log  (10^2 * 3.6549) + log  (10^3 * 1.4743)     10         10                     10  log  (x) = 2 + log  (3.6549) + 3 + log  (1.4743)     10             10                  10  log  (x) = log  (10^5) + log  (3.6549) + log  (1.4743)     10         10    10      10              10 Now, that's cool, because you can look up the logarithms of the numbers 3.6549 and 1.4743 from a table; add them; and then look up the inverse logarithm of the result.  Then multiply by 10^5 (by shifting the decimal place) to get the final product. This isn't such a big deal now, when cereal boxes give away calculators that can do it; but it's what made slide rules possible, and before that, it made a lot of calculations easy that would have been much more difficult.  

Math Dr. Ian goes on to explain why logarithms are useful for finding unknown quantities, by showing how they are analogous to inverse-multiplication (i.e. division):

Think about what makes division useful.  There's nothing you can do with division that you can't do more clumsily using multiplication in conjunction with guess-and-check.  When you just want to multiply things,   16 * 48 = ? that's easy.  When you only have one product and a result,   17 * ? = 592 division lets you invert the multiplication:   17 * ? = 592   ->  592 / 17 = ? Logarithms do the same sort of thing for exponents.  Sometimes you just want to raise something to an exponent, and that's easy:   12^4.9 = ? But sometimes you have the base and the result, and you need to find the exponent:   13^? = 6.3 You _could_ figure this out with guess-and-check; but logarithms let you get the result directly:   13^? = 6.3   ->   log  (13^?) = log  (6.3)                        13            13                               ? = log  (6.3)                                      13

The common logarithm in particular is so important because it operates on base 10, and so many of our concepts operate on powers of 10. For example:

the Richter scale

the Decibel scale

interest rate

Better Explained tells us that logarithms help to put numbers on “human-friendly” scales like the above.

The trick to overcoming "huge number blindness" is to write numbers in terms of "inputs" (i.e. their power base 10). This smaller scale (0 to 100) is much easier to grasp:

power of 0 = 100 = 1 (single item)

power of 1 = 101 = 10

power of 3 = 103 = thousand

power of 6 = 106 = million

power of 9 = 109 = billion

power of 12 = 1012 = trillion

power of 23 = 1023 = number of molecules in a dozen grams of carbon

power of 80 = 1080 = number of molecules in the universe

A 0 to 80 scale took us from a single item to the number of things in the universe. Not too shabby. (Source)

So how do we actually use this concept in real life?

1. To denote salary. We do this all the time! Whenever someone says they make a “6-figure salary,” they’ve used the common logarithm. According to Better Explained, “n-figure salary” is how we explain numbers in terms of their digits, that is, “how many powers of 10 they have (are they in the tens, hundreds, thousands, ten-thousands, etc.). Adding a digit means ‘multiplying by 10.′” This allows us to get “a rough sense of scale without jumping into details.” (Source)

2. Listening to music. “In the book The Joy of X – Steven Strogatz writes: Notice something magical here: as the numbers inside the logarithms grew multiplicatively, increasing tenfold each time from 100 to 1,000 to 10,000, their logarithms grew additively, increasing from 2 to 3 to 4. Our brains perform a similar trick when we listen to music. The frequencies of the notes in a scale – do, re, mi, fa, sol, la, ti, do – sound to use like they’re rising in equal steps. But objectively their vibrational frequencies are rising by equal multiplies. We perceive pitch logarithmically.” (Source)

3. The natural log and e. This is something that I’ll have to leave for its own post.

[language-of-math-blog]

Logarithm

This is a word that I never truly understood the meaning of. I’ve struggled to connect the concept to exponentiation, but this line from Wikipedia is helping solidify it in my brain:

In mathematics, the logarithm is the inverse operation to exponentiation, just as division is the inverse of multiplication. That means the logarithm of a number is the exponent to which another fixed number, the base, must be raised to produce that number. (Source)

In other words, the logarithm is the inverse of the exponent. The exponent is the power to which a root number is raised. The logarithm is the exponent to which the root number must be raised to produce the number in question.

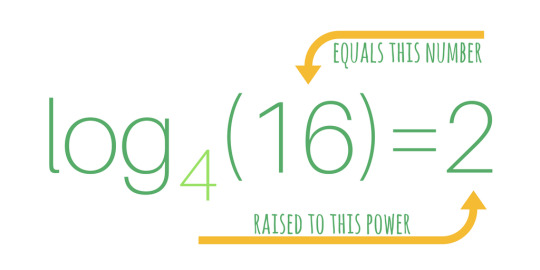
In a way, the operation to the right of “log” actually looks a little bit like an exponent, doesn’t it? We’ve got the number 4 nudged down a bit, and if you take the bottom of the number 4 as the base of a line, then the (16) seems to be raised a bit up and away from the number four. I want to make a suggestion for how to look at this operation, but first lets see if the etymology of “logarithm” can give us a bit more insight.

From etymonline:

1610s, logarithmus, coined in Modern Latin by Scottish mathematician John Napier (1550-1617), literally "ratio-number," from Greek logos "proportion, ratio, word" (see Logos) + arithmos "number" (from PIE *erei-dhmo-, suffixed variant form of root *re- "to reason, count")

Wiktionary asks us to compare:

rational +‎ number, ultimately from Latin rationalis + numerus. Compare analogous logarithm, from Ancient Greek. (Source)

So logarithm means “ratio-number,” but I still don’t understand why. Let’s see if the math words sites can give us a bit more insight.

At first glance it appears that the coined term is as confusing as I believed:

According to the OED2, "Napier does not explain his view of the literal meaning of logarithmus. It is commonly taken to mean 'ratio-number', and as thus interpreted it is not inappropriate, though its fitness is not obvious without explanation. Perhaps, however, Napier may have used logos merely in the sense of 'reckoning', 'calculation.'" (Source)

But it also states, later on in that same page:

According to Briggs in Arithmetica logarithmica (1624), Napier used the term because logarithms exhibit numbers which preserve always the same ratio to one another.

If we look at it from this perspective, I can kind of see why he would coin this term. There is a fixed relationship between the base, the exponent and the power. The ratio of the power to the base and exponent will always be the same.

[language-of-math-blog]

How Stephen Hawking’s Greatest Discovery Revolutionized Black Holes

“Increasing entropy, over time, should be okay, but decreasing it should be forbidden. The only way to ensure that would be by forcing an increase in the black hole’s mass to cause entropy to go up by at least the largest amount you can imagine.

The way that people working on that problem – including Hawking – assigned an answer was to make entropy proportional to the surface area of a black hole. The more quantum bits of information you can fit on a black hole, the greater its entropy was. But that brought up a new problem: if you have entropy, then that means you have a temperature. And if you have a temperature, you have to radiate energy away. Originally called “black” because nothing, not even light, can escape, now it became clear it had to emit something after all. All of a sudden, a black hole isn’t a static system anymore; it’s one that changes over time.”

Stephen Hawking may be most famous, today, for his popular accounts of astrophysics and cosmology, for his inspirational personal story, and for his overcoming of adversity and disability to achieve all that he has. But he was truly a tremendous physicist, and his contributions to our understand of black holes was truly transformative. His greatest discovery was that they weren’t merely static objects in space, but that they were active and evolving. They didn’t just absorb mass, but had an entropy, a temperature, and radiated energy away. How this occurred was far from intuitive, and it took a decade of research for Hawking to arrive at his incredible 1974 result, where he derived the existence of Hawking radiation. All of a sudden, black holes had a finite lifetime, and would eventually evaporate away entirely.

Here’s the story of Stephen Hawking’s greatest scientific find, and his greatest contribution to the canon of scientific knowledge. If you want to understand what he did and why it’s so important, you won’t want to miss this.

[language-of-math-blog]

it just occured to me that I always subconsciously thought that Stephen Hawking was going to live forever

[language-of-math-blog]

From Pat Ballew’s Math Words Site

[language-of-math-blog]

Radicals and the Repeat Bar

I learned something really interesting today!

The “square root” sign is not what I thought it was. The part denoting the square root is just this: √.

And that symbol is actually better referred to as the radical sign, or radix.

The part that we connect to the radix is the repeat bar, or vinculum:

The symbol actually has two parts, the radical and the horizontal bar. The symbol is written so that the two run together and appear as a single symbol, but the actual radical looks more like a check mark. The horizontal bar is a vinculum, just like the bar over a repeating fraction. (Source)

Pat Ballew expounds on the etymology of vinculum:

The word is from the diminutive of vincere, to tie. vinculum referred to a small cord for binding the hands or feet. The meaning in math is mostly unchanged from that original meaning, as the purpose of the repeat bar is to bind together the sequence of repeating digits. (Source)

I wish I had known this before; while I didn’t need it to understand the concept of radicals, it would have helped me to differentiate between square roots and cube roots, which use the same symbols, just with a number denoting the power.

The concept of the vinculum being separate from the radical also solidifies the concept of the radical and what exactly is going on. When you see the number 16 inside of a radix + vinculum symbol, you can understand that the repeating bar is telling us that the number underneath it is repeating (4*4). I’m not sure if this is exactly the right way to think about it, but visualizing those numbers repeating under that vinculum is helping me to understand the concept, so I’m going to go with it for now.

[language-of-math-blog]

Radicals

I googled the etymology of “radical” and the explanation that Google provided immediately made the concept clearer to me:

late Middle English (in the senses ‘forming the root’ and ‘inherent’): from late Latin radicalis, from Latin radix, radic- ‘root.’

“Forming the root.” The number that, when multiplied by itself, forms the base of the exponent. It is the “root,” the “base,” of that operation.

We can take this word, “root,” and deepen our metaphor:

The Indo-European root werad was used for the branches or roots of plants. Later it was generalized to mean the origins, or beginnings of something whether it was physical or mental. In arithmetic the root of a number is the number that is used to build up another number by repeated multiplication. (Source)  

According to the above source by Pat Ballew, the Indo-European word for root “werad” was used by al-Khowarizmi, and then translated into Latin as radix, which is where we get the word “radical.”

The “root” of a square number (i.e. 16) is called its “square root,” and the root for the squared-number 16 is 4. Similarly, the root for a cubed number is called the cube root, and the root for the cubed-number 8 is 2.

[language-of-math-blog]

Exponent

The term EXPONENT was introduced by Michael Stifel (1487-1567) in 1544 in Arithmetica integra. He wrote, "Est autem 3 exponens ipsius octonarij, & 5 est exponents 32 & 8 est exponens numeri 256" (Smith vol. 2, page 521). (Source)

When I was looking for the etymology of exponent, here is what I found:

From etymonline:

1706, from Latin exponentem (nominative exponens), present participle of exponere “put forth”

From Wiktionary:

From Latin expōnēns, present participle of expōnō (“to expose; to exhibit, display, set out; to explain”), from ex- (“out, away”) + pōnō (“to lay, place, put”).

Reading through these definitions (and having no knowledge of Latin), I tried to reason through what choosing this word for the concept of exponentiation might have meant. It seemed fitting that we would “put out” the number that would raise the base, that we would “place it away” from the base so that it could be seen.

After searching online I ran into this website by math instructor Pat Ballew, who appears to agree with this interpretation:

Exponent is the union of the Latin roots exo(out of) + ponere (place). The literal interpretation is to make something visible or obvious. That seems to be what happens when the index is raised "out of" the line. The English word expound, from the same source, means to make clear. An exponent is also used in English to describe a person who explains or interprets.

I love how he makes the connection to the second meaning of exponent, which is to expound. I was unable to draw the line myself, but I like how it has that additional meaning of “to make something clear.” You make the exponent clear by raising it away from the base. (He notes that this interpretation may not sit well with everyone, as can be seen on this page by Dr. Peterson, one of the Math Doctors at the Math Forum. However, I agree with it wholeheartedly, as it was the connection that made the most intuitive sense to me.)

[language-of-math-blog]

Systems of Equations

As I prepared to teach students about working with systems of equations, I reflected on last year’s students and came to a painful realization- there were several students who just never really got what they were doing. Sure, most students got pretty good at using the substitution method or the elimination method to solve for two systems of equations, but even for those who could do well with test questions, did they really understand at a conceptual level what they were doing? It was humbling to realize that for most of them, the answer was probably no, they didn’t. (Source)

Unfortunately, I was one of those students. And in many ways, I still am.

Linear systems is something that has never really made sense to me, and even now when I see them, I have no idea what I’m supposed to do with them. I’m sure that I have to “solve” it in some way, but I have no idea what I’m solving, or why.

After failing to understand a linear systems problem on Microsoft’s AI Math Essentials Course, I figured it was time for me to break this concept down and really try to understand it.

While I applaud the teacher in the above quote for giving students hands-on exploration around linear systems, I still believe that approach would be insufficient for someone like me. As always, I need to understand the why behind the concept. So what if I see that there are solutions that fit more than two linear systems? What are those “solutions”? And what the hell is the “system” representing anyway?

I’m going to try to find out.

Sciencing.com has an article titled “10 Ways Simultaneous Equations Can Be Used in Everyday Life.”

Simultaneous equations are a system of equations that are all true together. You must find an answer or answers that work for all the equations at the same time. For example, if you’re working with two simultaneous equations, even though there may be a solution that makes one of the equations true, you must find the solution that makes both equations true.

Alright, this is the basic definition and goal behind linear systems that I can understand on a conceptual level. When presented with a linear system, find the “solutions” (numeric values of variables) that make ALL equations in the system true.

But how does this matter in real life?

Take this example (source):

Anne is trying to choose between two phone plans. The first plan, with Vendafone, costs $20 per month, with calls costing an additional 25 cents per minute. The second company, Sellnet, charges $40 per month, but calls cost only 8 cents per minute. Which should she choose? 

The previous article had a list of the different ways in which linear systems could be used to solve real-world problems. However, they didn’t lay out specific examples, with numbers and everything, so it was hard for me to make the connection.

But an example like the above one is much easier to see. Already, I can figure out how to write the equations:

vendafone = 20 + 0.25x sellnet = 40 + 0.08x

I know it’s customary to write the coefficient+variable term first, but this way makes much more sense to me, especially when thinking about the fixed cost as a “bias parameter” given my background in machine learning. Perhaps that was all I had to do—rearrange the “grammar” of the mathematical “sentence” so that I could read it properly.

But I’m still not sure what this system is trying to solve. Both of these equations seem linearly independent. How does the price of one phone company depend on the other? Is she trying to have a fixed number of minutes x? Is she hoping to pay only a certain amount of money?

If you look at the graph of the two equations, you can make an intuitive guess that if she’s going to be using a lot of minutes each month, she should go with Sellnet, and if not, then she should choose Vendafone (which is cheaper if you use fewer minutes).

I had a gut feeling that I should set the two equations equal to each other, because “vendafone” and “sellnet” could be represented by the same variable, “cost” or “y.” If I rewrote the equations as

cost = 20 + 0.25x cost = 40 + 0.08x

then I could set the two equations equal to each other and get

20 + 0.25x = 40 + 0.08x

After solving this, I get x = 117.65 (rounded up), which is the number of minutes the source says would make the phone plans cost the same.

On the graph, we can see that this x-value is exactly the point at which the two lines intersect.

In that case, I can see how systems of equations are looking for values of x that make both equations “true.” In this case, both equations have a y-value that is equal when x is a certain value.

What about the question that stumped me in the course?

Apples cost 5 cents, and oranges cost 15 cents. In total, one spends 75 cents on nine pieces of fruit. How many apples and how many oranges did one buy?

5apple + 15orange = 75fruit

apple + orange = 9fruit

I was stumped on how to solve this for a while. But then it looks like I can rewrite the second equation to be apple = 9fruit - orange, and then substitute it into the first equation. (I’m pretty sure substitution is one of the typical methods one could use for solving linear systems, but I’m glad I was finally able to figure it out on my own.)

I solved the linear system to get 3 oranges, and extrapolated that to 6 apples.

I watched the instructor do the elimination method on the course, and I didn’t like it at all. It was just too much work to take out one of the variables. I think I prefer the substitution method. It’s more intuitive to me. I wonder if I’ll come across a linear system where I’m required to use the elimination method. I hope not! But it would be good to practice it to know how to do it, even though I prefer the substitution method.