mathdevelopment

[mathdevelopment]

Statement Expressions

This post uses code blocks, which might not come out very well in your Tumblr feed. For the best experience, view this post on mathdevelopment.tumblr.com

Let’s consider a hypothetical C-like language. Here's some example code so you get the idea:

while (true) { print("Pick a number!"); let x = input(); if (x > 0) { print("You chose " + x); break; } else { print("Sorry, pick a POSITIVE number"); } }

We understand this code by breaking it up into statements and control structures. Using the antlr parsing syntax, we might parse this program as:

entry: (control | statement)*; control: while | if; while: WHILE '(' expression ')' block; if: IF '(' expression ')' block (ELSE block)?; block: '{' (statement | block)* '}'; statement: (let | break | call) ';'; let: LET NAME '=' expression; break: BREAK; call: expression '(' callargs? ')'; callargs: (expression ',')* expression; expression: operator | atom; operator : operator '>' atom | operator '<' atom | operator '=' atom | operator '+' atom | operator '-' atom | operator '*' atom | operator '/' atom ; atom : '(' expression ')' | call | NAME | NUMBER | STRING | BOOL ;

That might be a lot to take in, especially if you've never seen that syntax before, but if you stare at it long enough, you should be able to get the gist of what's going on. Take your time if you need it. We'll be coming back to this later.

This model seems intuitive. It's how we as humans understand the program, and it properly conforms with all of our needs. But of course you're thinking something's up. Why would this blog post author go through all the trouble to explain something that his readers intuitively know already?

Something is up, and I'll explain that in a bit, but first I want to put up a sort of disclaimer. This first model works. It works very well. This is the parsing model (plus or minus a few things) that languages with this kind of syntax tend to use. This post is not about why the intuitive parsing strategy is bad, but rather to explore an alternative parsing strategy, and what benefits and drawbacks it may have.

Here's a question: why do we have a semicolon at the end of each line? It denotes the end of a statement, right? Some languages have done away with it and been fine, but proponents argue that the semicolon improves legibility, and maybe makes syntax errors more apparent. Plus, it can avoid the widely-hated significant whitespace, one of the only things that can bring C, LISP, and Malbolge developers together.

Okay blog author, you've made your point. You like semicolons and hate python. What are you getting at?

Semicolons are used for terminating statements, but what if we viewed it another way? What if instead of saying that a semicolon ends a statement, what if we said it lets a new statement begin? This seems like a subtle distinction, and it is, but it's a distinction that lets us bridge to a more powerful concept. Semicolons indicate both the end of a statement and the start of a new statement. If you want to run two statements, you need a semicolon between them. To join them, in a sense. The semicolon is the statement join operator.

You might have some concerns at this point, and I'll get to those, but first let's think about the syntax. Here's what I propose:

entry: statement?; statement : LET NAME '=' expression ';' statement? | BREAK ';' statement? | call ';' statement? | WHILE '(' expression ')' block statement? | IF '(' expression ')' block (ELSE block)? statement? | ';' statement? // empty statement ; block: '{' statement? '}'; // everything else as before

We can represent everything we could represent in the old parse syntax, but now instead of having a list of statements, we have a tree of statement expressions.

Now I know what you're thinking: either, "but how does let work?", or "hehe... I know how let is gonna work... this is cool."

Thank you for your input group 2, but I'm going to cater to group 1 for now. You may not have noticed it, but the grammar I chose for statement expressions didn't actually need to be as verbose as I wrote it. An alternative, more compact version could have worked just as well:

statement : (let | break | call) ';' statement? | (while | if) statement? ;

But that would have presented a problem once we got to implementation. You see, using let instead of var or def like many other languages do was not accidental. In functional programming, let has the connotation of "let [variable = value] in [expression]". And that's exactly what we're doing here. let passes information to the trailing statement expression about that variable we just declared, sort of like opening a new scope. If we had used the more compact parsing grammar, the definition in let wouldn't have been able to access the trailing statement very easily (of course, it still would have been possible, but doing what we're doing here with the original grammar also would have been possible; it just wouldn't have been very pretty).

Using indentation to represent the tree structure of our expression statements, we get this for the original program:

while (true) { print("Pick a number!"); let x = input(); if (x > 0) { print("You chose " + x); break; } else { print("Sorry, pick a POSITIVE number"); } }

You might have a new concern, and understandably so. This sample program was carefully created as to avoid something common in imperative languages and much less common in functional languages:

let x = input(); if (x < 0) { let y = x*x; x = y; } print(x);

Mutation.

We're stuck, right? This is the end? Our exploration of treating statements as expressions has come to a close?

No, not quite.

Our statements are expressions, and expressions return something. So what data type does x = y return? State. It returns the state of x having been assigned to y. Every time we evaluate the next statement in the tree, we pass it the state of the previous one, and at the end we return not a value, but the newly constructed state after the statement has been evaluated. When we enter a block we create a new state whose parent state is the state passed into the block's statement, and the block returns the parent of the state returned from its last statement.

Update: Let me interject for a moment to clarify something. I'm assuming here that the state is an immutable data structure. It doesn't need to be of course, but this whole state-passing system starts to feel extremely over-engineered if it is not.

Say we input 3:

// For state, we use the format [parentState, [myBindings]] let x = input(); // returns [global, [x: 3]] if (x < 0) { let y = x*x; x = y; } // returns [global, [x: 3]] print(x); // returns [global, [x: 3]]

But if we input -3:

let x = input(); // returns [global, [x: -3]] if (x < 0) { let y = x*x; // returns [[global, [x: -3]], [y: 9]] x = y; // returns [[global, [x: 9]], [y: 9]] } // returns [global, [x: 9]] print(x); // returns [global, [x: 9]]

So why do we want this? What's the point? Part of it is a sense of idealism. There's a general feeling that immutability is good practice, and this brings immutability to... mutation, I suppose. In some cases it could be easier to develop a language with this structure. Static code analysis could catch bugs that would be harder to detect with mutable state.

But there are drawbacks too. This doesn't permit shared program state across threads, for example, though this model could be extended with some sort of "unsafe assignment" mechanism to mutate a shared state. And if a compiler developer is seeking optimal performance, this model will likely be reduced down to exactly what we had before anyways.

In the end, as mentioned near to the start of this post, this alternative model is not "better" than our more traditional sequential statement model, but it's not worse either. It's an alternative approach, a new way to tackle an old problem. But that's also kind of the point. Even problems which appear to have only one solution can often be elegantly solved with alternative approaches. The solution is not defined by the problem, the problem is defined by the solution.

[mathdevelopment]

Lambda Calculus for Programmers

I’m a programmer far more than I am a mathematician (funny given my blog name, huh?), and functional programming has lately become really interesting to me. However, whenever I try to learn more about it, it always comes back to the mathematical models which describe functional programming, and as someone without much knowledge of that kind of stuff, it can get really tiring to need to scour wikipedia for half an hour just to get a rough idea of what someone is talking about over and over.

But I don't want other people to need to struggle through that process like I have (and like I certainly will even more in the future), so I'm going to try making these posts explaining these mathy kinds of things in a way that programmers will be able to understand. To start out, I'll begin with lambda (λ-) calculus.

Basic constructs

First, let's define a few constructs and their programming (pseudocode) counterparts:

Variables can be almost anything, but are usually letters with optional subscripts. These are the same in λ-calculus and programming. a

a;

These are just anonymous functions. everything between the λ and the . are parameters, everything after the . is the return value. (λx.y)

fn (x) { return y; }

You can also have multiple parameters: (λxy.z) But that's really just syntactic sugar for: (λx.(λy.z)) or λx.λy.z Meaning it actually would be:

fn (x) { return fn (y) { return z; } }

Function calls don't require parentheses. Just put a function next to a variable and the function is called with that variable. s t

s(t);

a b c

a(b(c));

Of course, parentheses are permitted for clarity, and are sometimes necessary: (f (g h)) j or (fgh) j

(f(g(h)))(j);

And finally (for now), what I'll call the "substitution operator" though I'm sure mathy people won't love that name. I should note that this construct is not strictly necessary for λ-calculus, but you may see it around. x[x := y]

let x = y; x;

Converting this one to pseudocode is a bit tricky, and I think that using my example could just add confusion depending on the person. Just think of it as "whenever I see the left side, replace it with the right side." The left side must be a variable, so my pseudocode does work, but feel free to keep it or leave it.

If this seems complicated and you don't completely get it yet, that's fine. Just keep going and you'll get the hang of it.

α-conversion

Or "alpha-conversion."

The semantics of doing this that you'll generally see are pretty complicated and they involve this thing called a "free variable," but let's skip all that nonsense. You already know how to do α-conversion intuitively if you ever refactor your variable names. The one thing to watch out for is variable shadowing, where two variables in different scopes have the same name.

For example: λx.λx.x = λz.λx.x = λx.λy.y = λz.y.y

fn (x) { return fn (x) { return x; } } // is equivalent to fn (z) { return fn (x) { return x; } } // is equivalent to fn (x) { return fn (y) { return y; } } // is equivalent to fn (z) { return fn (y) { return y; } }

Simple, right?

β-reduction

Or "beta-reduction."

β-reduction is almost simpler than α-conversion, though like the substitution operator, it's hard to show in pseudocode. It's essentially the idea that any function call can be inlined, where its contents are expanded into the call site. λx.x q = x[x := q] = q

fn (x) { return x; }(q) // apply beta-reduction let x = q; x; // is equivalent to q;

Really the better way to understand this is not through a direct translation, but through a pseudocode example that doesn't have a super easy-to-understand λ-calculus equivalent:

fn do_something (x, y) { let z = x + y; return z - 5; } do_something(3, 8); // apply beta-reduction let x = 3, y = 8; let z = x + y; z - 5; // is equivalent to let z = 3 + 8; z - 5; // is equivalent to 3 + 8 - 5;

In case you're wondering and want to challenge yourself, here's the λ-calculus equivalent, assuming +, -, 3, and 8 are already bound:

f := λxy.(λz.(- z 5) (+ x y)) f 3 8 →η λxy.(λz.(- z 5) (+ x y)) 3 8 →β λz.(- z 5) (+ 3 8) →β - (+ 3 8) 5

η-conversion

Or "eta-conversion."

η-conversion means that if two things have the same outputs for all of the same inputs, they can be swapped for one another. For example, by η-conversion: λx.(f x) = f

Definitions of η-conversion you'll see online will probably talk about "free variables" (as will definitions for α-conversion and β-reduction) but as long as you understand static (or lexical) scope in programming, you'll be fine for η-conversion.

But what is a free variable?

The formal definition for free variables is a bit tricky, so let me put it in my own words:

A free variable is any variable which is used before it is bound in the target expression.

For example, if I just write x, x is free, as it has no binding. However, if I write λx.y, x is not free as it has been bound within the expression. y however, is free. If I were to write λx.x x, x would not be free within the sub-expression λx.x, but it would be free overall because the binding within the function doesn't apply for the call outside of the function.

The reason I haven't explained why you care about free variables is because as a programmer, you intuitively know how scopes work and the rules governing them. Mathematicians though, in order to maintain logical rigor, need to explicitly spell it out, and they use free variables as a construct to assist in that.

Conclusion

In this post I've explained the basic rules of λ-calculus, but there's still a lot (and I mean a LOT) more to learn. This article was almost entirely built from the lambda calculus Wikipedia article, and there's a lot more from it that I didn't cover such as arithmetic, boolean logic/predicates, tuples, fixed-points/recursion, and more.

Next week: Haskell.

Just kidding. I'm not going anywhere near that language.

[mathdevelopment]

Random Math Topic of the Day: Eigenvectors

Note: Most posts on this blog focus on a programming project. This one is more about what I researched while making a programming project, linked at the end. I'm sorry if you like this kind of content less.

Welcome to #RMTotD, prounounced rm-tot'd.

So what is an eigenvector anyways? Good question. For a given transformation matrix (pretty much any square matrix, though typically we use 2x2, 3x3, and 4x4 only), there are a number of eigenvalues up to but not exceeding the size of the matrix (except for when there are infinite eigenvalues). E.g. a 2x2 matrix can have up to 2 eigenvalues, a 3x3 matrix can have up to 3 eigenvalues, a 4x4 matrix can have up to 4 eigenvalues, etc.

But what is an eigenvector, you say as I still haven't actually told you what an eigenvector is despite the fact that I implied that I would tell you.

Well, one way to understand it is that an eigenvector is a vector whose direction is the same whether or not it has been transformed. That is,

\[ \text{Let } b=Ma; \; \hat{a}=\hat{b} \]

Google says that an eigenvector is "a vector that when operated on by a given operator gives a scalar multiple of itself." That scalar is called its eigenvalue, represented by \(\lambda\):

\[ Mv_{\lambda = k} = kv \]

All vectors which match the above definition are eigenvectors, and the collection of all of those vectors (hint: there's an infinite number of them for each eigenvalue. Just change k!) are called the eigenspace. Wow, sounds cool, huh? An eigenspace is easily represented by \( tv_{\lambda=k} \) (for eigenvalue \(k\)) but there are actually a bunch of different ways to represent an eigenspace that all pretty much mean the same thing.

"But wait!" you say frantically. "This is mathdevelopment.tumblr.com! There would never be a post on mathdevelopment.tumblr.com that didn't involve programming!"

Right you are! I produced a little site to help visualize eigenvectors for one of my former teachers to use, but I figured I would post about it here too. You'll need to sit through some more fun properties of eigenvectors before you get the juicy interactive graphs though. After all, this is mathdevelopment.tumblr.com, not randomprogrammingprojectsthatunlockeddecidedtomake.tumblr.com!

Eigenvectors have a cool property where if you have \(n\) eigenvalues in an \(n\text{x}n\) matrix, any point in the relevant \(n\)-dimensional space can be represented as a linear combination of the eigenvectors, and the transformed point will also be a combination of the initial eigenvectors multiplied by their associated eigenvalues:

\[ \text{For} \;\; v_{\lambda=a}+v_{\lambda=b}+\dotsc=v; \] \[av_{\lambda=a}+bv_{\lambda=b}+\dotsc=Mv\]

Cool.

Okay, fine, you can have the site. Click here.

[mathdevelopment]

Markov Mimic

the eighteenth century and only the rule voting rights for example welcomed people started compared to say that the puritan separatists fled to the massive continent was made through the united states constitution was only once the natives the states constitution was much more liberal views but when hernán cortés lots of the seventeenth century most people of finding and the way the different motives for example welcomed people like

That's what my "Markov Mimic" program produced when I fed it a couple of essays I wrote back at the start of my AP US History class. Is it meaningful? No. Could it be improved to be meaningful? Not really. Is it cool anyways? Sure. So how did I generate that blurb of nonsense from a couple essays? The answer is in the title of the program: Markov chains. This is a Markov chain (courtesy of Wikipedia):

So how does this work? It's a set of states (labeled 1, 2, and 3 in the example) with probabilities directing from each state to another, or itself. The probabilities also sum to 1. This is a way of modeling probabalistic state changes mathematically. So how does this apply to Markov Mimic? Well, I just generate a Markov chain, but instead of numbers, each state is a different word.

The program goes through each word in the block of text (my essays) and figures out the chance that each word will go to another word. Then, it just randomly cycles through this for as long as I want. There are more complex ways of handling probabilities to produce more gramatically correct (but not more meaningful) results, but my next-word algorithm can produce some entertaining results anyways.

[mathdevelopment]

The Turing Completeness of FAI

"Turing complete" is a term that means that the given machine or system can solve any turing-computable problem, which is basically any problem that can be solved (unsolvable problems are often paradoxical, such as the Halting problem).

Proving that a language is turing complete is trivial for languages with mutable collections: all you need to do is create a turing machine in that language. Purely functional languages with only immutable types, such as FAI, have it tricker though. While it is (often) possible to produce functions which copy a collection type with a slight alteration, it's not pretty, and there's a lot of computation that goes into copying things. Fortunately, there are Turing Machine equivilents.

One of those equivilents is a cellular automaton called rule 110. In a way, rule 110 is one of the simplest possible ways to prove that a language is turing complete, especially when mutable data types aren't freely avaliable. I'm not going to get into exactly what rule 110 is, but reading the wikipedia page and looking at a playground demo should help you figure it out.

So in order to prove FAI is turing complete, I just need to implement rule 110. It's not pretty, but here's the code:

rule110(row, initial)={ initial if row = 0; rule110(row, "0"+initial) if initial[0] = "1"; rule110(row, initial+"0") if initial[length(initial)-1] = "1"; rule110(row-1, ((state, index, rule) -> { "" if index = length(state); rule("0" + state[index..index+1]) + self(state, index + 1, rule) if index = 0; rule(state[index-1..index] + "0") + self(state, index + 1, rule) if index = length(state)-1; rule(state[index-1..index+1]) + self(state, index + 1, rule) otherwise; )(initial, 0, neighbors -> { "0" if neighbors="111"; "1" if neighbors="110"; "1" if neighbors="101"; "0" if neighbors="100"; "1" if neighbors="011"; "1" if neighbors="010"; "1" if neighbors="001"; "0" if neighbors="000"; "" otherwise; )) otherwise;

And in TeX form:

Large version

That's long and complicated, but anyone with a math background should be able to read the TeX version. Just try!

Anyways, that's all for now. You can get the latest version of FAI and try this out yourself at this link.

[mathdevelopment]

Quick update on FAI

Time for a quick update.

FAI is now on GitHub. Feel free to contribute to it as much as you would like. Language discussion can also be held in the issues tab.

That's it.

[mathdevelopment]

Functional, Algebraic, and Interpreted language

Which is abbreviated to FAI (pronounced fī) or FAI lang.

Over the past while, I've been creating my own language, and while it's certainly not complete by any means, it's ready for a showcase and first draft specification.

Objective

Many people have said that we need to make CS more ingrained in math education, but people generally haven't provided any seamless solutions. Rather than integrating CS with math, these proposals tend to just teach CS and math side-by-side. That's better than nothing, but it's not good enough. To truly teach them together, you need a language that looks so much like algebra that students can use it intuitively without much thought. That's where FAI comes in. It strives to be a purely functional language with algebraic syntax. While it has features not commonly found in algebra (like string manipulation), the core principle is to provide a high-level language that looks and acts like algebra, just with a heavy emphasis on functions.

It can't solve equations for you. That's not the point. If you want something to solve equations for you, use a calculator. FAI allows you to implement your own derivations as functions, and call them as necessary. For example:

plus_minus(a, b) = (a+b | a-b) quadratic(a, b, c) = plus_minus(-b, sqrt((b^2)-(4*a*c)))/(2*a)

And then insert \(x^2-3x+2=0\)

quadratic(1, -3, 2) > (2 | 1)

And it returns the roots: 2 and 1. Don't worry about the syntax the roots were returned in for now, just know that both 2 and 1 were returned by the quadratic function.

FAI is also purely functional, making it great for teaching the functional programming concepts which are applicable in almost every high-level field. lambda exists in a readable format, and is used as any other function. In fact, all built-in functions are simply lambdas with external definitions that have been attached to a name:

quadratic > lambda(a, b, c: <expression>) sqrt > lambda(a: <external>)

This allows for usage of higher-order functions, like so:

combine_three(a, b, c, func)=func(func(a,b),c) combine_three(1, 2, 3, lambda(a, b: a + b)) > 6

This can also teach about recursion, using a piecewise-like syntax for the conditions:

factorial(x)={x<=1: 1; x * factorial(x-1)} factorial(5) > 120

There exist other more semantically relevant features, but not ones that get in the way of the core purpose of the language, which is to serve as a link between programming and algebra.

Features and WIP Specification

The following is a detailed list of current language features at the time of writing. If you aren't interested in this, scroll down a lot to find information on the future of this language.

Scope

Scope in FAI is slightly confusing, though it has been designed to keep the purely functional aspect of the language where a function may only use its own arguments.

Globals

The following are both global definitions, but they do very different things:

var_name = 10 func_name() = 10

The first is called an outer argument, while the second is a global function. The scope of an outer argument is restricted to the outermost scope, while the scope of a global function extends to everywhere. For example:

x = 10 f1(a) = a + 1 f1(x) // Using an outer argument in the outer scope works > 11 f2(a) = x + a // Oops! Can't use an outer argument inside a function f2(1) > InvalidName: The name x is neither a named function nor an argument. f3(a) = f1(a) + 1 // Using a global function in a function is okay though f3(10) > 12

This means that these two lines technically act differently:

f(x) = x+1 // Can be used anywhere l = lambda(x: x + 1) // Can only be used in the outer scope

Function

A function may only access its arguments and any globally defined function. All functions also have access to self, which is always defined to be the lambda of the function being called, except in the outer scope. While this would mostly be used for lambda recursion, technically any function has access to its self.

Calls

A call is anything directly evaluated by the REPL. However, because expressions have fairly intuitive evaluation, this part will be exclusively focused on non-expression calls.

Declaration

The syntax for declaring a global function is:

fname(arg1, arg2, arg3, ... argn) = <expression>

The syntax for declaring an outer argument is:

oname = <expression>

Memoization

Certain recursive functions can take a long time to execute. For example, the following call can take 5 seconds to execute:

fibo(x) = {x <= 2: 1; fibo(x-1) + fibo(x-2)} fibo(32) // This is REALLY slow > 2178309

However, it can be sped up through a trick called memoization. In many languages you would have to implement this yourself, but FAI will memoize functions for you if you add the keyword memo before the function definition.

memo fibo(x) = {x <= 2: 1; fibo(x-1) + fibo(x-2)} fibo(400) // Lightning fast. If it wasn't memoized, it would longer than the heat death of the universe to finish. > 1.76023680645014E+83

Update

Attempting to redefine a name in the outer scope will throw an error without the update keyword.

x = 10 f(x) = x + 1 f(x) > 11 x = 5 // Can't do this! > DefineFailed: The update keyword is required to change the definition of a function or outer argument. update f(x) = x + 2 // This is okay though. f(x) > 12

Because FAI is lazily evaluated, it can break memoization if a memoized function relied on a now updated function. To fix this, the update keyword may also be used in conjunction with memo to refresh the memoization of a function, or when used on a non-memoized function, it can change that function to be memoized:

g(x) = 1 memo f(x) = g(x) f(2) > 1 update g(x) = x f(2) // Oops! Memoization stored a value wrong! > 1 update memo f f(2) // There we go. > 2

Termination

Calls may be terminated with either an EOF or ;.

Types

All types support = and ~= as "equals" and "not equals," which both return booleans. The one exception is unions, which handle those operators in the same special form that they handle all other operators.

Numbers

FAI numbers are complex. The literal may contain a single optional decimal point as well as an i at the end for imaginary values. While they may be represented in a complex form like 4+2i, keep in mind that that form is really just an addition of 4 and 2i. +, -, *, /, and ^ operators are legal. - may also be used as a prefix (e.g. -10) to negate the value of a number. The comparison operators >, <, >=, and <= are unique to numbers, and unlike the other numerical operators, they return booleans. It should be noted that comparing the values of complex numbers with imaginary components is impossible in algebra, which is discussed in the challenges section of this post lower down.

Booleans

In FAI, booleans act as one might expect. They can be either true or false. + serves as the boolean "or" operator and * serves as the boolean "and" operator, with the ~ prefix being "not." Booleans are the only type for which all operators and prefixes used on it will return the same type.

Strings

FAI strings are currently barely working and should not be used. However, they do support + for concatenation, and use the "str" literal. You know what, don’t even try to use strings. They’re so broken in this version.

Lambdas

"Lambda" will often be used interchangeably with "function" in FAI, as any lambda is also a function and any function is also a lambda. Lambdas only support the call syntax, which is a special form postfix notation.

Unions

Unions really deserve their own category. The point of a union is to be multiple values in a single object. For example, the quadratic function should return up to two numbers, even though it can only return one thing. To solve this, it returns a union of both valid answers. This union may only be manipulated as if it were a single value. Unions may only contain distinct values, and if a union only has one distinct value, it dissolves into that one value. Unions also may not be nested, and any nested union will be automatically flattened upon evaluation. They are defined using the union literal (val1 | val2 | val3 | ... | valn).

Piecewise expressions

For if, else, and cond, FAI has piecewise expressions. The syntax is as such: {cond1: <expr1>; cond2: <expr2>; cond3: <expr3>; ...; condn: <exprn>; <exprelse>}

Lambda expressions

A lambda expression may also be known of as an anonymous function. It allows you to create a function as an object rather than as a definition, which can be extremely powerful in many different use cases. Other than piecewise expressions, the lambda expression probably has the most special form of any expression in the language: lambda(arg1, arg2, arg3, …, argn: <expression>)

Challenges and Future Goals

Challenges

Currently, large amounts of recursion will result in a stack overflow. I'll need to restructure the functional call stack to operate iteratively in the future.

Currently, non-real numbers are compared by using their magnitudes. However, this means that (5+2i) >= (5-2i) is true, and even worse, (5+2i) >= (-5+2i) is also true. A possible fix would be to throw an error when comparing non-real numbers, but I would rather not do that if possible.

The common algebraic syntax 2x and 2(x) are not legal. They should be. However, making them legal would require a moderate reworking of how expressions are parsed.

Algebra has a single-argument pipeline syntax called composition (e.g. \(f \circ g(x)\)) that should be added. However, finding a suitable replacement for ∘ may be tricky given that o can be used in names and * is used for multiplication. . may work.

Decisions

I'm currently debating over whether I should add vectors and matrices. I have a syntax figured out for them, but I'm not sure I want them to be part of the language.

What should happen if part of a union throws an error?

Should a null-like type be introduced? There are benefits from a language perspective, but it's not terribly algebraic.

A function should be able to take in a variable number of arguments, though a syntax and data structure to handle that is tricky to decide on.

Bugs and currently unimplemented features

Order of operations is not necessarily obeyed.

String indexing successfully parses, but has not yet been implemented.

The REPL only has support for one-line calls, despite multi-line calls being fully parseable.

Extraneous content at the end of an call will sometimes parse even though it's not legal code.

Complex math, especially regarding exponents and sqrt, may result in near-zero imaginary errors. These errors could cause major issues with comparison operators, and these forms are just generally less readable.

Lambda expressions should be memoizable.

= and ~= do not work with lambdas. They should.

Unions should not ever be directly transferred as arguments, even in user-defined functions. They should always be run separately and then reunified, like for external functions.

Strings are just completely broken right now and need to be fixed.

How to use the FAI REPL program

Download and unpack the FAI REPL.

Install the .NET Core 2 runtime.

Run dotnet FAIrepl.dll in the unpacked folder using whatever your system's command line is.

[mathdevelopment]

Player movement

This is one entry in a multi-part series. If you haven't read the start of the sandbox demo series, start reading here.

The time has finally come to let the player move around. There are a few ways to handle movement in a 2D game, depending on the type of game. If I were making a precision platformer, I would probably just want fixed speed movement, but I’m not so I’ll go for acceleration with a maximum speed.

Even with that approach there are multiple options though. Here's an equation I've used in the past:

\[v\left(t\right)=a+fv\left(t-1\right)\]

//This is what it would look like in code: player.Velocity *= f; // 0 < f < 1 player.Velocity += a;

\(a\) is the acceleration of the player or entity and \(f\) is the "decay" or friction, generally set to a high decimal value like 0.8. The maximum velocity in this approach is equal to \(\frac{a}{1-f}\). I'm sure you could prove that with limits or something, but I'm going to take the "if it seems to work it's probably right" approach. If I let \(a=1\), the formula evaluates to:

\[v\left(t\right)=s\left(1-f\right)+fv\left(t-1\right)\]

where \(f\) represents the accleration and \(s=v_{\max}\). Oh, and if we're going for low-level optimization, I can cut out a multiplication operation with this simplification:

\[v\left(t\right)=s+f\left(v\left(t-1\right)-s\right)\]

Mathematically, this formula works. In practice, the code is going to have more trouble with it. \(t\) is supposed to represent time, but computers don't always have the same time gap between frames. If I were to lock the framerate I could ignore that issue, but nobody likes framerate locks. To fix this, I'll move outside of algebra and into programming math. Oh, and let's change \(s\) to \(m\) and \(f\) to \(a\) while we're at it.

\[v\rightarrow m+a\Delta t\left(v-m\right)\]

\(\Delta t\) can really be in any time format I want, as long as I set \(a\) accordingly.

So let's put this into code! I'll start with horizontal movement first, as that doesn't really require that I actually implement physics.

if (keyboardState.IsKeyDown(Keybinds.Left)) targetSpeed -= 10; if (keyboardState.IsKeyDown(Keybinds.Right)) targetSpeed += 10; player.Velocity = new Vector2(targetSpeed + (0.9f * (float)gameTime.ElapsedGameTime.TotalSeconds * (player.Velocity.X - targetSpeed)), player.Velocity.Y); player.Position += player.Velocity.ToPoint();

But that didn't work. I mean, it worked in terms of the scaling (my math was right!) but the actual speeds and positions that things were at were wrong. After some testing (some of which involved an actual stopwatch) I realized the problem. I had multiplied the acceleration by the time step, but not the velocity when moving the player. But after I did that, the player wouldn't move at all. I immediately realized the issue: the distance moved per time step is less than one. The positions of entities are stored as points (for reasons that will be explained later), and points use integer x and y values, rather than Vector2s which consist of floating point numbers. I wanted to preserve the exact-ness of the position but still allow for decimal positions, so I decided to comprimise with this little bit of code:

public Vector2 Velocity { get; set; } public Point PointPosition { get { return Position.ToPoint(); } }

C# properties are beautiful, aren't they. I may regret this change later on, but I'll deal with it then. For now, I have other issues. Almost everything is working properly at this point, but the acceleration isn't visible. I changed \(a\) to 0.999f, but even that still wasn't noticable. The time step was too small for my large \(a\) values. At this point I also realized another problem. In the case in which a time step takes longer than one second (which should never happen in theory), everything will break. I'm sure speedrunners would love that, but I'm not making this for speedrunners. I need to guarantee that my \(a\) term is always less than one. I also need to guarantee that my \(a\) term is properly distributed over a second no matter how many updates are contained within that second.

I thought about this puzzle for a while until I finally came to my conclusion: If this is possible to solve, I don't know how to do it. If you can think of a solution to this, tweet me or ask me the answer, because I seriously have no idea. For now, I'm just going to remove the time step factor from the acceleration. Goodbye delta t, you will be missed.

\[v\rightarrow m+a\left(v-m\right)\]

For testing purposes, I'm going to make the player speed be 24 tiles/s or 1.5 chunks/s.

Of course though, the player's velocity shouldn't change mid-air, should it? Or if it does, it should change MUCH slower. My formula doesn't easily allow for things like air control, so while I could probably implement it by changing the \(a\) term while the player isn't grounded, I'll just add a "is player grounded" check before trying to change their velocity. Note that I haven't actually implemented any code that tells me if the player is grounded. I'm just using placeholder variables for now.

Now that I'm done with horizontal velocity (yes, all of that was just for horizontal velocity), I'm going to move on to vertical stuff. I might be able to just use straight acceleration, but I don't really want the player to be clipping through the ground. There are "ray"cast solutions to that, but I'm just going to assume that the player won't be going at ground clipping speeds for now. Is that ignorant? Yes. Do I care? Yes, but I'm willing to overlook it for now.

So I'm going to use raw acceleration anyways, even though I said it was a bad idea. Otherwise it's gonna feel like the player is hanging on to a bunch of balloons whenever move. How does 1 chunk/s2 sound for acceleration due to gravity? I think it sounds fine, so I'm gonna use that.

Let's go back to the collision from last time, specifically this line:

anyCollide = true;

Instead of just checking if there are any collisions, I'm also going to eject the player from the tile. This essentially means that if a player is inside of a tile, I'm going to move them just enough outside of the tile that they are resting right beside the tile. This is where my concern about using Position and PointPosition came from. When using floats for physics, there is often an issue of vertical jitter where the player is displaced just out of the tile, falls back into the tile the next frame, and then is displaced outside in the next frame. Hopefully that won't happen here, but I should keep in mind the possibility that it could.

But how will I perform ejection in the first place? It's not actually quite as hard as it sounds. Remember that stackoverflow answer that was actually a gamedev stackexchange answer that I linked in the previous post? That specifically mentions vertical ejection, but I'll apply the same idea for both axes. However, I won't eject on both axes. If I did, stuff like this would happen all the time:

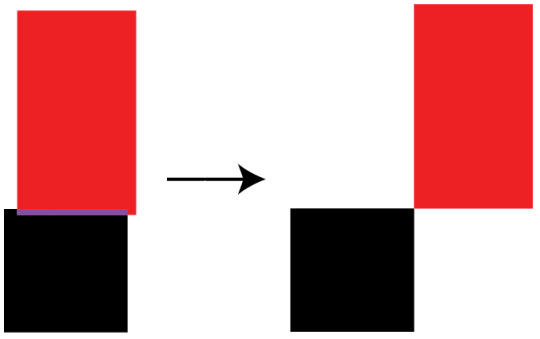
Where what I really want is this:

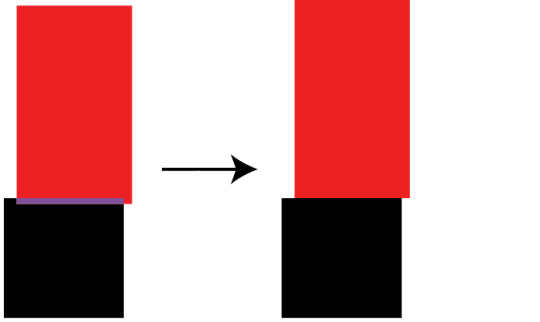
To fix that, I'll look for the axis which has the lowest intersection, and eject on that axis. I'll know which direction by checking which side of the original entity center the intersection is on.

if (currentRect.Intersects(tileRect)) { anyCollide = true; Rectangle intersection = Rectangle.Intersect(currentRect, tileRect); if (intersection.Width < intersection.Height) { if (intersection.Center.X > currentRect.Center.X) { e.Position += -Vector2.UnitX * intersection.Width; } else { e.Position += Vector2.UnitX * intersection.Width; } e.Velocity *= Vector2.UnitY; } else { if (intersection.Center.Y > currentRect.Center.Y) { e.Position += -Vector2.UnitY * intersection.Height; } else { e.Position += Vector2.UnitY * intersection.Height; } e.Velocity *= Vector2.UnitX; } }

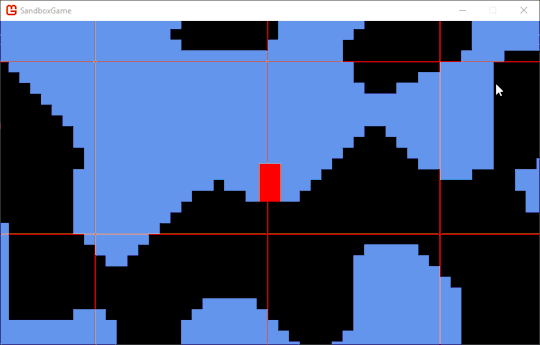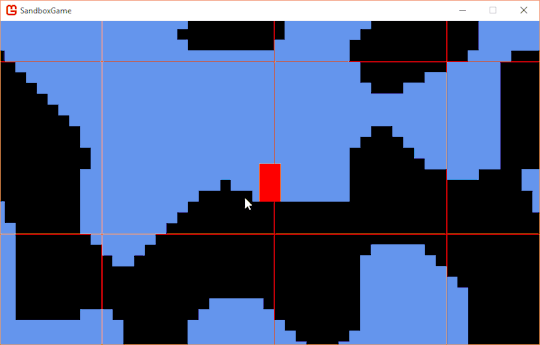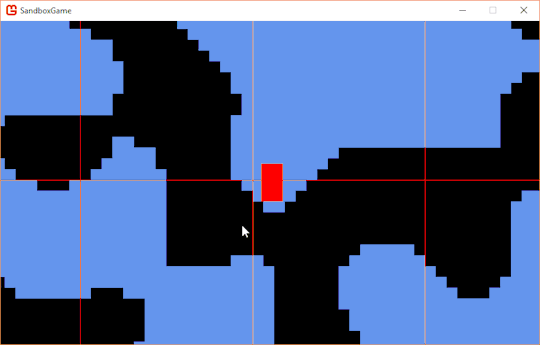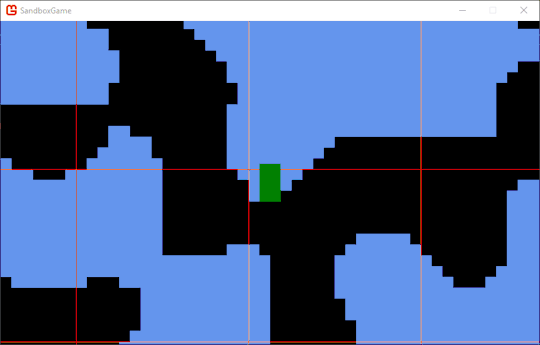
It works! My problem now is that I have no jump. Adding a jump is easy, but making it only work while the player is grounded is trickier. You might not have noticed the flashing the the gif above due to the framerate of the gif, but the character was flashing between red and green every frame. This is actually a side effect of the jitter I mentioned earlier. The frame after the player is ejected from the ground, they're no longer intersecting the ground, and so they appear red again.

However, this is actually sort of weird behavior due to the semantics of how I programmed and arranged my code. By best guess has to do with the time step being so quick that -16 * UNIT_SIZE * gameTime.ElapsedGameTime.TotalSeconds, the delta-v on the y axis, is less than one.

After some quick testing, I discovered that my hypothesis was in fact incorrect. However, though I may have been wrong, I was certainly on the right track. Each frame, the position is not changed by the velocity, but by the velocity times the time step. Therefore, it would actually take four or five frames to accumulate enough delta-y to intersect the player again.

Creating a fix to this issue which is ignorant of the framerate is pretty tricky. One option is to do an additional intersection check with a rectangle expanded by one unit in every direction. Hopefully this new check can actually replace the old one, as if there is a collision with no intersection, the intersection width or height would be zero, as per the documentation.

I should be able to say that an entity is grounded if the collision pushes them up, or the height of an intersection is zero. It works... I think.

After a bit of testing I decided to increase the acceleration due to gravity, and everything seems to be working fi- oh wait, no, that's not right. I have accidentally implemented wall jumps. Let's fix this by checking the ejection direction of the expanded collision rectangle, and performing the old collision that we know worked.

And it works! The last change that I'm going to make for the post is to change the current lack of air control into a slower acceleration air control. I can do this by just cranking up the \(a\) value from earlier really high while the player isn't grounded.

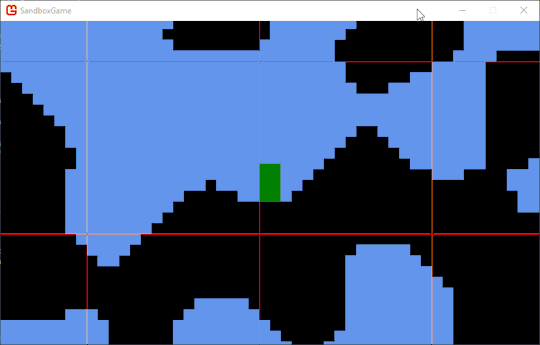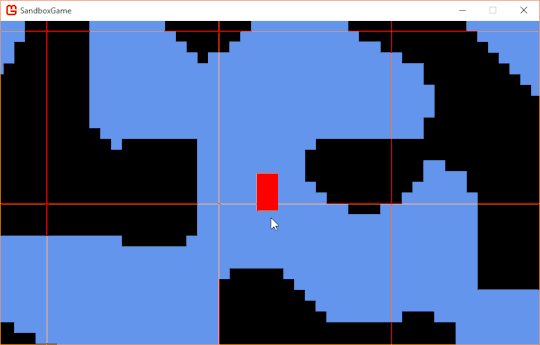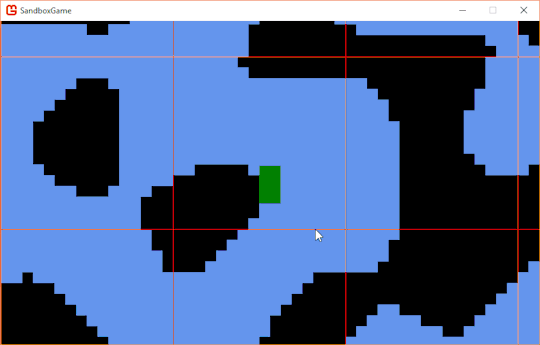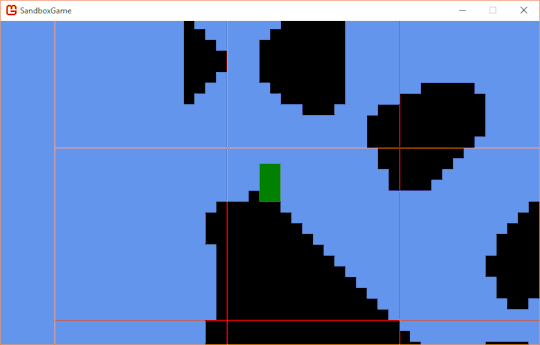
// These code blocks are getting way too long. bool anyCollide = false; e.Grounded = false; Rectangle entityRect = e.GetCollisionRect(); for (int x = entityRect.Left; x < entityRect.Right + Game1.UNIT_SIZE; x += Game1.UNIT_SIZE) { for (int y = entityRect.Top; y < entityRect.Bottom + Game1.UNIT_SIZE; y += Game1.UNIT_SIZE) { Tile t = GetTile(new Point(x.FloorDivide(Game1.UNIT_SIZE), y.FloorDivide(Game1.UNIT_SIZE))); if (t != null && t.HasCollision) { Rectangle currentRect = e.GetCollisionRect(); Rectangle expandedRect = currentRect.InflateThrough(1, 1); // Uses extension function of Rectangle.Inflate to make a clean one-liner. Rectangle tileRect = new Rectangle(x.FloorDivide(Game1.UNIT_SIZE) * Game1.UNIT_SIZE, y.FloorDivide(Game1.UNIT_SIZE) * Game1.UNIT_SIZE, Game1.UNIT_SIZE, Game1.UNIT_SIZE); if (expandedRect.Intersects(tileRect)) { Rectangle expandedIntersect = Rectangle.Intersect(expandedRect, tileRect); if (expandedIntersect.Height < expandedIntersect.Width && expandedIntersect.Center.Y > expandedRect.Center.Y) e.Grounded = true; anyCollide = true; if (currentRect.Intersects(tileRect)) { Rectangle intersection = Rectangle.Intersect(currentRect, tileRect); if (intersection.Width < intersection.Height) { if (intersection.Center.X > currentRect.Center.X) { e.Position += -Vector2.UnitX * intersection.Width; } else { e.Position += Vector2.UnitX * intersection.Width; } e.Velocity *= Vector2.UnitY; } else { if (intersection.Center.Y > currentRect.Center.Y) { e.Position += -Vector2.UnitY * intersection.Height; } else { e.Position += Vector2.UnitY * intersection.Height; } e.Velocity *= Vector2.UnitX; } } } } } }

And in honor of another game created using XNA, here are some vertical hoiks.

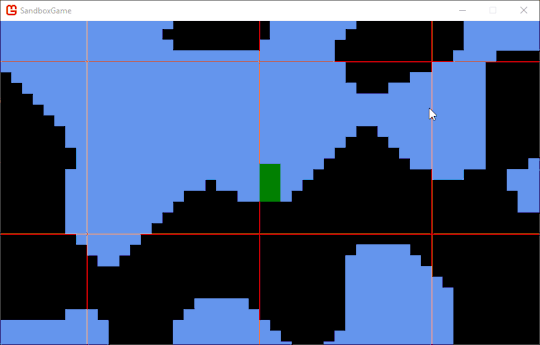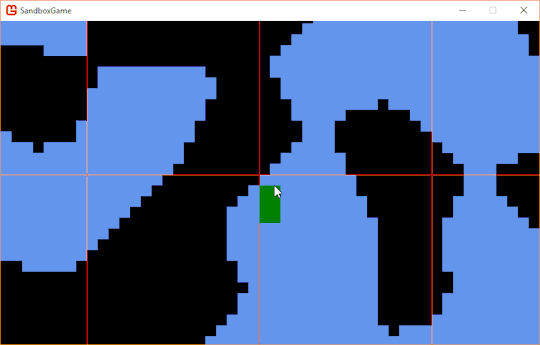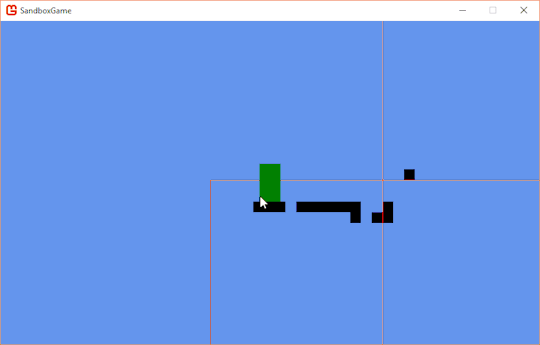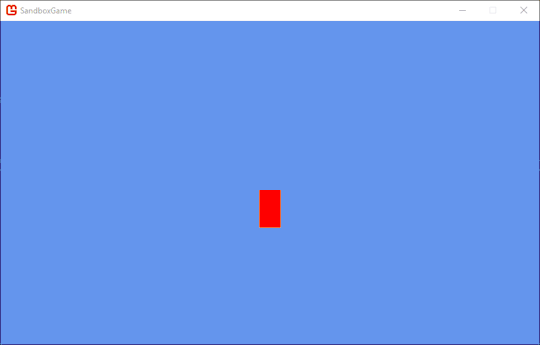
They're a bit harder to control.

[mathdevelopment]

Collision Detection

This is one entry in a multi-part series. If you haven't read the start of the sandbox demo series, start reading here.

It's time to add physics! Although before that, I should really create a player of some kind. A static keybinds file should do the trick for a modular control system. For the sake of modularity, I'll also make a template "entity" class which the player will extend. This will take quite a bit of boring infrastructure work, so I'll spare you the details on that and get right into the fun stuff.

Fortunately for me, AABB collision isn't something I need to implement myself. Monogame has a built-in Rectangle type, which is a 2D version of BoundingBox. The answers to this stackoverflow question are going to help me out so I don't need to draw diagrams on paper for thirty minutes.

The more interesting thing is what to detect collisions on. Obviously I could detect the collision between each entity and each tile, but that seems highly excessive. With a reasonable number of entities I'd be doing tens or even hundreds of thousands of comparisons per tick. I should be able to instead take advantage of the chunk structure from the previous post. From that I can narrow it down to at most four chunks, and usually just one. In the worst case, I would have a maximum of about 1000 comparisons per entity. That's not great, but it's much better.

I can chop that number down even more though. I don't need to compare a collision if the tile is more than a single unit away from the edge of an entity. This would be a little weird to represent visually due to the top-left alignment of everything in this game, though the math doesn't care how things are aligned as long as they're all aligned in the same way.

bool anyCollide = false; Rectangle entityRect = e.GetCollisionRect(); for (int x = entityRect.Left; x < entityRect.Right; x += Game1.UNIT_SIZE) { for (int y = entityRect.Top; y < entityRect.Bottom; y += Game1.UNIT_SIZE) { Tile t = GetTile(new Point(x.FloorDivide(Game1.UNIT_SIZE), y.FloorDivide(Game1.UNIT_SIZE))); if (t != null && t.HasCollision) { if (entityRect.Intersects(new Rectangle(x, y, Game1.UNIT_SIZE, Game1.UNIT_SIZE))) { anyCollide = true; } } } }

So this works mostly. However, you'll notice that I created the FloorDivide extension function for integer division. Most integer division truncates the result. E.g. 13 / 2 = 6; -7 / 3 = -2. However, I don't want that. As I've mentioned earlier in this series, I need to use consistant rounding if I don't want negative positions to act differently from postitive ones. FloorDivide just divides two integers where instead of truncating the result, it floors it. This collision system works for the most part, but has some noticable flaws and quirks:

Ah ha! Some debugging visuals later and I figured out that the issue had to do with the entity not checking all of the necessary tiles. I added an extra Game1.UNIT_SIZE to both for loops and took it out for a spin:

So it's now checking the correct tiles for collision, but it's not actually detecting intersections properly. Because it's much more likely that I'm doing something wrong than that a widely used game development library buit on top of another widely used game development library is doing something wrong, I decided to take another look at my intersection code.

Well that didn't take very long to fix. My x and y were being inconsistantly operated on, so I floored them both down to the "closest" unit size. Here's my updated intersection statement:

if (entityRect.Intersects(new Rectangle(x.FloorDivide(Game1.UNIT_SIZE) * Game1.UNIT_SIZE, y.FloorDivide(Game1.UNIT_SIZE) * Game1.UNIT_SIZE, Game1.UNIT_SIZE, Game1.UNIT_SIZE))) { anyCollide = true; }

Alright. So now I can detect collisions efficiently and accurately. However, that wasn't really what I set out to do. I wanted to make physics. However, because this post is getting a bit long (okay not really but it's taken me longer than it should've to make), I'll end this one here. Stay tuned for collision part two!

[mathdevelopment]

Chunk chunk chunk chunk chunk...

This is one entry in a multi-part series. If you haven't read the start of the sandbox demo series, start reading here.

Remember how last time I said I was gonna add collision detection? I've changed my mind. Implementing a chunk structure seems like a much better thing to do first.

Chunks will be good for me because of my problem with the tile grid before. My current system only stores the tiles that exist, which is good for memory, but it's not so good for basically anything else. A better method would be to have chunks laid out in that way, and for each chunk to have a full grid structure. Sort of like a List. I'll make chunks a nice 16x16 tiles.

Well that looks... uneventful. I've had to disable my tile creating/destroying code for the time being, as it currently doesn't work with the chunk system. I'll make functions to handle placing and removing blocks later, but for now let's just try to place some noise. I'll be using the FastNoise script, as it's easy and I just need an easy noise generator right now.

// World initialization code FastNoise noise = new FastNoise(); world = new World(); for (int x = -100; x < 100; x++) { for (int y = -100; y < 100; y++) { if (noise.GetSimplex(x * 5, y * 5) > 0.06f) world.SetTile(new Point(x, y), t); } }

// A portion of World.cs public void SetTile(Point p, Tile t) { Point chunkPos = new Point((int)Math.Floor(p.X / 16f), (int)Math.Floor(p.Y / 16f)); foreach (Chunk c in ChunkList) { if (c.ChunkPosition.Equals(chunkPos)) { c.TileGrid[p.X.Mod(16), p.Y.Mod(16)] = t; return; } } Chunk chunk = new Chunk(chunkPos); chunk.TileGrid[p.X.Mod(16), p.Y.Mod(16)] = t; ChunkList.Add(chunk); } public Tile GetTile(Point p) { Point chunkPos = new Point((int)Math.Floor(p.X / 16f), (int)Math.Floor(p.Y / 16f)); foreach (Chunk c in ChunkList) { if (c.ChunkPosition.Equals(chunkPos)) { return c.TileGrid[p.X.Mod(16), p.Y.Mod(16)]; } } return null; }

As I was implementing that, I encountered some issues.

Yes, I really did need a world class with tile placement functions. That has been added.

I needed a way to explore the map. I added dragging functionality to do this.

The modulo operator is really a remainder operator. I have implemented a correct modulo function as an extension.

public static int Mod(this int x, int m) { return (x % m + m) % m; }

Now that I have this in place, I'll reintegrate the old click to replace feature.

Oh, and while I'm changing things, let's remove that static. I don't really need it anymore.

I suppose the next step in this would be to have automatic unloading and loading of new chunks, though I don't even have a player to handle that yet. Currently I just have a camera, and while it could make sense to base chunk loading on where the camera is, I really think I should just do it properly and implement something like physics first. You know, the thing I said I'd do last time.

Please provide feedback, and if I'm approaching this completely incorrectly, tell me! I have a twitter too, @The_Unlocked. Bye for today.

[mathdevelopment]

The origins of a test

So I was thinking, "hey, whatever happened to XNA?"

The answer, of course, is that XNA is never going to be updated again. I already knew that. I was more wondering if there was any XNA-like successor.

And there is! It's called monogame. After loading it up in visual studio, I found out that it's not simply a spiritual successor, it's more of a continuation of XNA. I mean, just look at these imports (or usings) in the auto-generated game file:

using Microsoft.Xna.Framework; using Microsoft.Xna.Framework.Graphics; using Microsoft.Xna.Framework.Input;

But now is the question of what to make. I'm not just going to install monogame, create a blank solution, and then just leave it. How about... a Terraria clone!

Actually that seems kind of hard. How about just a plain 2D tile-based sandbox game thing. That seems a bit easier.

But I wouldn't be making this post here if I was making something easy, now would I? The answer is no, I wouldn't. The first roadblock I hit was trying to figure out how I actually wanted to handle rendering the blocks and making physics work. Let's just start with rendering for now though.

There are three ways that I initially think of making this work. The first is having a grid covering the entire visible screen, which I will populate with the appropriate tiles each update (doing it in the draw call is unnecessary as the camera can't move in-between updates). The general loop would look like this:

// In order to allow everything to be done in the (x, y) order, my 2D arrays will be in a column-first layout. for (int x = 0; x < renderGrid.GetLength(0); x++){ for (int y = 0; y < renderGrid.GetLength(1); y++){ if (renderGrid[x,y] != null) spriteBatch.Draw(renderGrid[x,y].Texture, new Vector2(x * tileSize, y * tileSize) - new Vector2(cameraPosition.X % tileSize, cameraPosition.Y % tileSize), Color.White); } }

That seems slow though. Like, really slow. The draw area will often be sparse when the player is above ground, and even when they're below ground it offers a very limited performance boost, if any, over method 2:

//Let's assume that renderTiles has been created in the logic loop, like with renderGrid in method one. foreach (Tile tile in renderTiles){ spriteBatch.Draw(tile.Texture, (tile.Position * tileSize) - cameraPosition, Color.White); }

That seems better. Possibly a lot better. Again, the logic loop will be given quite a bit of work, but it might have less work as it doesn't need to populate a grid, with the additional rounding math. But there should be a way to do this easier.

for (int i = 0; i < bakedTextures.Length; i++){ spriteBatch.Draw(bakedTextures[i], bakedPositions[i], Color.White); }

Method three might be the fastest, and it would also be useful for collision, but I really don't want to create a realtime baking algorithm just to see how well it performs, if at all. I might need to in the future, but hopefully not for now.

I'll go with method two for now. I'm also not going to worry about sorting out off-screen tiles from the on-screen tiles for now, as that shouldn't be too problematic to work on further down the production line.

Ah, that beautiful cornflower blue. Anyways, better move the camera over a bit. (0, 0) is always the top-left corner.

Alright. That looks fine. I just created a big rectangle of tiles. I added a little bit of random noise to the color of each tile to make sure I didn't mess anything up, and as it turns out I didn't. Great!

But this is pretty boring. Time to add some kind of interaction! How about a thing where I can click, and if a tile exists it deletes it and if a tile doesn't exist it adds one. This would be a nice place for that grid setup now that I think about it. In fact, using chunks would probably be an ideal setup for this. I suppose I'll add those later. Currently I'm only dealing with a few hundred tiles at most, so I don't need to worry about that right now.

// This is a truncated version of my actual code to remove stuff not currently relevant. All real code will be truncated in this way. MouseState lastState; int TILE_SIZE = 16; Vector2 camera_pos = new Vector2(160, 160); protected override void Update(GameTime gameTime) { var mouseState = Mouse.GetState(); if (lastState == null) lastState = mouseState; if (mouseState.LeftButton == ButtonState.Pressed && lastState.LeftButton == ButtonState.Released) { bool found = false; foreach (Tile t in tileList) { if (t.Position == ((mouseState.Position.ToVector2() - camera_pos) / TILE_SIZE).ToPoint()) { tileList.Remove(t); found = true; break; } } if (!found) { tileList.Add(new Tile(basicTile, ((mouseState.Position.ToVector2() - camera_pos) / TILE_SIZE).ToPoint())); } } lastState = mouseState; base.Update(gameTime); }

You'll notice that I didn't place any tiles on the left or top of the initial block. This is because of float to int truncation during the conversion from Vector2 to Point. For example, (int)1.5f becomes 1 while (int)-1.5 becomes -1. The positive number decreases in value while the negative number increases. The floor function is really what I would prefer, so I guess I'll write an extension function for that.

public static Point ToPoint(this Vector2 v, Func f) { return new Point(f.Invoke(v.X), f.Invoke(v.Y)); }

And now every call of .ToPoint() is just replaced with .ToPoint(x => (int)Math.Floor(x)). Perfect.

Well that's it for today. Please leave comments somehow. If all else fails you can just send me messages through the "ask me stuff" page. Next time I think I'll try to work on getting a player in here, and maybe even some primitive colision detection.

[mathdevelopment]

Hello, World!

Hello, Unlocked here. I've tried to start up some blogs before, but they haven't really gone anywhere. However, I think this will be more successful. I'm going to be publishing posts about my programming experiments and projects here. As the name of the tumblr suggests, I'll be trying to work through the more mathy and algorithmic parts of programming so you don't have to. All of my struggles and successes will go here so you can learn from my mistakes.

Oh, and if anyone knows of a good theme for programming blogs, send 'em to me! Currently my code blocks look like this:

Wow, a code block. Also like I'll probably need syntax highlighting so yeahh... I'll figure out how to do that later.

Anyways, Unlocked out. Byee!