mathwithicecream

[mathwithicecream]

The moving sofa problem has finally been solved!

[mathwithicecream]

Forget every single trig identity.

[mathwithicecream]

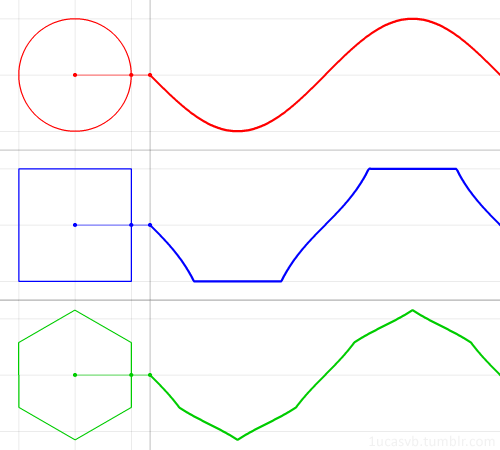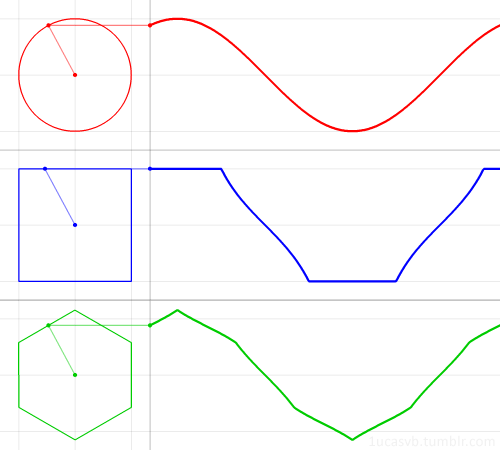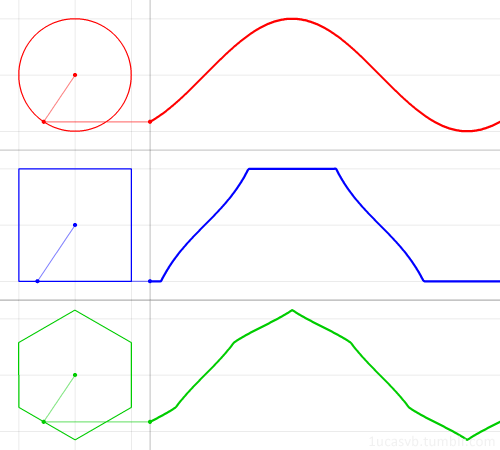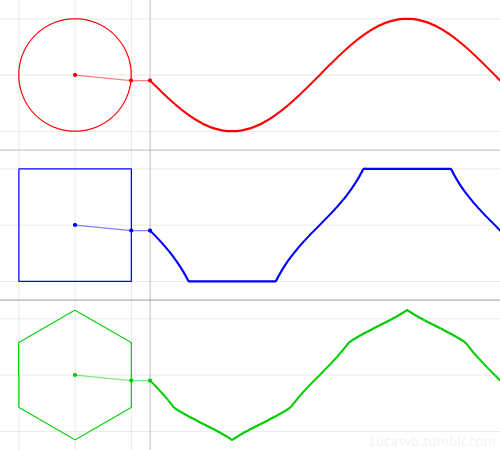
The familiar trigonometric functions can be geometrically derived from a circle.

But what if, instead of the circle, we used a regular polygon?

In this animation, we see what the “polygonal sine” looks like for the square and the hexagon. The polygon is such that the inscribed circle has radius 1.

We’ll keep using the angle from the x-axis as the function’s input, instead of the distance along the shape’s boundary. (These are only the same value in the case of a unit circle!) This is why the square does not trace a straight diagonal line, as you might expect, but a segment of the tangent function. In other words, the speed of the dot around the polygon is not constant anymore, but the angle the dot makes changes at a constant rate.

Since these polygons are not perfectly symmetrical like the circle, the function will depend on the orientation of the polygon.

More on this subject and derivations of the functions can be found in this other post

Now you can also listen to what these waves sound like.

This technique is general for any polar curve. Here’s a heart’s sine function, for instance

[mathwithicecream]

Mathematical fun fact of the day:

If you draw a regular 4k+2-gon and add a regular 2k+1-gon inside it sharing a side, then the innermost vertex of the 2k+1-gon will be the center of the 4k+2-gon. For example, you can add two 2k+1-gon so that they meet in the middle:

[mathwithicecream]

A Curious Fact About Semicircles!

[mathwithicecream]

Btw I have a twitter where I sometimes post about math (but it’s mostly nonsense)

[mathwithicecream]

Holy shit???

[mathwithicecream]

Moessner’s magic

Start with a list of all nonzero natural numbers. Cross out every second one—the even numbers—and take the cumulative sum of the resulting sequence. The resulting list is 1, 3 + 1 = 4, 5 + 4 = 9, 7 + 9 = 16… and these numbers should look familiar: they’re precisely the square numbers!

In 1951, Alfred Moessner discovered the following similar procedure. Start with the same nonzero natural numbers, and cross out every third one. Add the numbers as before, and now cross out every second one. Then you’re left with the third powers of the natural numbers.

Starting with every fourth number results in the fourth powers, and Moessner conjectured (well, said that his not-so-easy proof would follow later) that this holds in general: starting with crossing out every k-th number, summing, crossing out every (k–1)-th number, summing… finally gives you the k-th powers.

What happens if we start with different numbers? Funnily enough, if we start with crossing out the triangular numbers 1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10… (every time incrementing the step size with 1) then we find the factorial numbers 1! = 1, 2! = 2 × 1 = 2, 3! = 3 × 2 × 1 = 6, 4! = 4 × 3 × 2 × 1 = 24…

If we increment the increment in the step size with 1 every time, so that we cross out 1, 1 + 3 = 4, 1 + 3 + 6 = 10, 1 + 3 + 6 + 10 = 20… the resulting sequence may not look that familiar. These numbers are the superfactorials 1!! = 1, 2!! = 2! × 1! = 2, 3!! = 3! × 2! × 1! = 12, 4!! = 4! × 3! × 2! × 1! = 288…

Finally, crossing out the square numbers gives us another unfamiliar sequence. However, notice that the squares are given by 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1, 1 + 2 + 3 + 4 + 3 + 2 + 1… and that the resulting numbers are precisely 1, 1 × 2 × 1, 1 × 2 × 3 × 2 × 1, 1 × 2 × 3 × 4 × 3 × 2 × 1…

[mathwithicecream]

I haven’t done anything with this account for quite a while, but a year and a few months ago I was feeling a continued depression about not making it into a PhD program.  A week or two after that Post I was accepted into what honestly is and was my dream program, and a few hours ago I got an email that I passed all of my preliminary/qualifying exams, so I’m now officially in the program.  I really don’t know what to say, but I unironically am just feeling so #blessed or whatever right now.

And just as I did at my absolute lowest (yikes), no matter what you’re going through, I absolutely believe in you and support.  If you ever want to message me, I’m here at least as an ear (I get anxious replying to people, I’m sorry, but just know that if you’ve messaged me I really appreciate and believe in you <3 )

[mathwithicecream]

little collection of false proofs!!! see if u can spot the mistakes

Keep reading

[mathwithicecream]

Perspective Grad Student Visit Tips

Step 1: do the really annoying apps. the rec letters matter like 6 times more anyways. Step 2: Wait Step 3: Wait some more. Check email obsessively

Now that we’re pass that, grad school visits are very exciting but also rather…. a lot. Most of mine were unusually early (I have one of three left) so might as well use that everyone else’s advantage and some tips, notes, and questions to ask while you’re visiting.  Note that I am a pure math student going into a PhD program.

1. It will be exhausting. it’ll also be really exciting but it’s impossible to deny that meeting a ton of new people and finding out so much info in a very small space of time is exhausting. So keep that in mind

2. You’re not actually trying to impress everyone. Be friendly and engaged and curious but the grad program is actually trying to entice and inform you now. A good department is also honest about the reality of being a student there.

3. Pay attention to the current grad students. Do they seem happy? What are their opinions? No one knows what being a grad student somewhere is like more than the grad students themselves. Also, as the grad director said last weekend, professors know what they want the program to be but the students know what the program is.

4. Skim over the grad student handbook beforehand if you can find it and have time but don’t worry about knowing a bunch of stuff before going. They will tell you all the important bits. Probably several times

5. If you’re going on a visiting day, also pay attention to other perspective students since if you go, a lot of them will be your cohort and man do you get familiar with your cohort.

6. Do your best to go to optional things. They’re usually a good opportunity to talk to people and ask questions informally and they tend to be a lot of fun (leaving early from them might also be a good option depending on the situation)

Now some useful questions (from a mix of profs and grad students at my undergrad, things that occurred to me, and a few random sources such as the AMS) I tried to arrange the questions in a way that makes sense but they’re mostly just random still

For professors

Retention and graduation statistics

What do graduates tend to go on to do?

Seminars and the sort available

How does the advising system work?

Examination requirements (prelims, quals, comprehensives, etc)

Taking courses that aren’t strictly math?

Fellowship opportunities

These can mostly also be asked of grad students of course

For current students

What do you do besides work?

What’s normal for hrs of TA work per week (this tends to vary a ton within a program but still worth asking)

What mental health services are available and how much/are they actually accessible?

How about physical health services? Health insurance?

Accessibility to things like campus gym or university recreation events?

Do you feel like the department is supportive? What about specifically of women/gender minorities/etc?

Do people usually work together while they’re in classes? How about once they’re doing research? How about research collaboration beyond the department?

How are prelims/quals/whatever they’re called

Are there resources about what apartment complexes are good?

How is grocery store/restaurant/etc access? If you’re used to a particular type of non-americian food ask about that in particular (I really want a decently sized asian grocery store within a reasonable drive)

Is the stipend livable? In addition, who you ask is going to be very important here since I realized that I got answers from a lot of applied students on my last visit and fewer pure students but industry/national labs/etc tend to pay significantly better than normal TAships

[mathwithicecream]

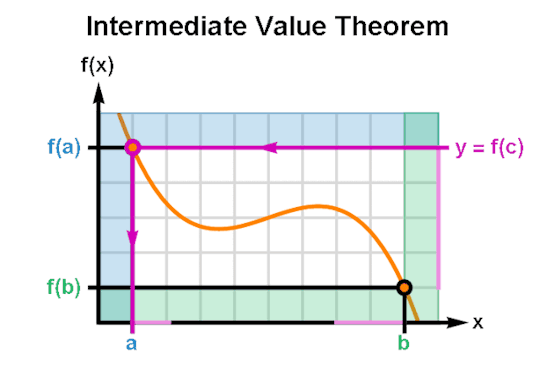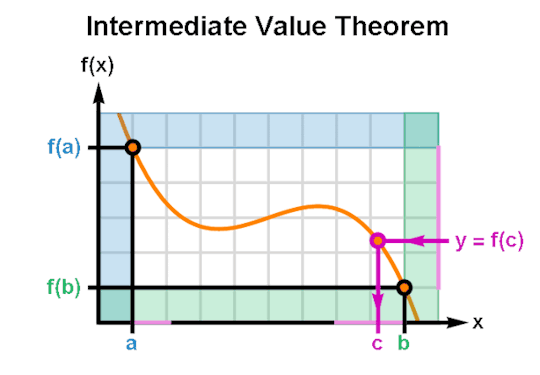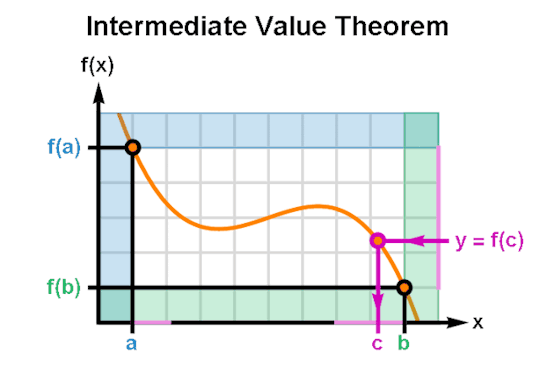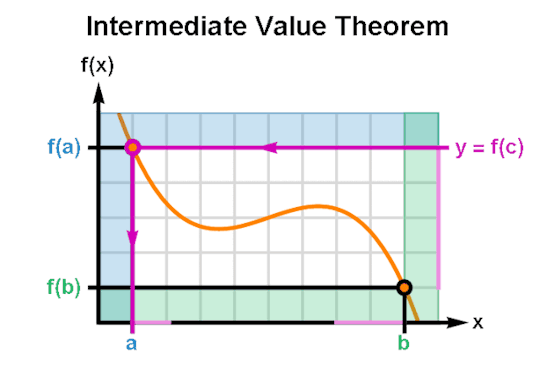
The Intermediate Value Theorem guarantees that for every real number “y” between two outputs of a real continuous function f(x) there exists at least one value “c” between the corresponding inputs such that y = f(x) when x = c.

(GIF Description: The graph of a function f(x) as it ranges from x = a to x = b. Per frame, an output value y between f(a) and f(b) is shown to intersect the curve f(x) for some x = c. As the GIF animates, y sweeps across the range of f(x) and indicates a value of c for every y.)

[mathwithicecream]

Given a function f(x) which is continuous on an interval [a,b] & differentiable on its interior, the Mean Value Theorem guarantees there exists a value c in that interval such that the line tangent to the function when x = c is parallel to the line drawn between ( a , f(a) ) and ( b, f(b) ). (GIF Description: A function f(x) is plotted from x = a to b, and a red line is drawn b/w its endpoints at ( a , f(a) ) & ( b , f(b) ). A point tracing f(x) carries a compass that records the tangent’s slope relative to the red line. When their slopes are equal, x is labeled c. In the first GIF, the function has a single maxima. In the second GIF, the function has multiple extrema.)

[mathwithicecream]

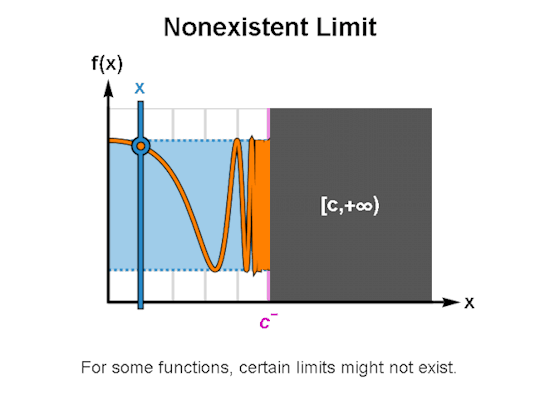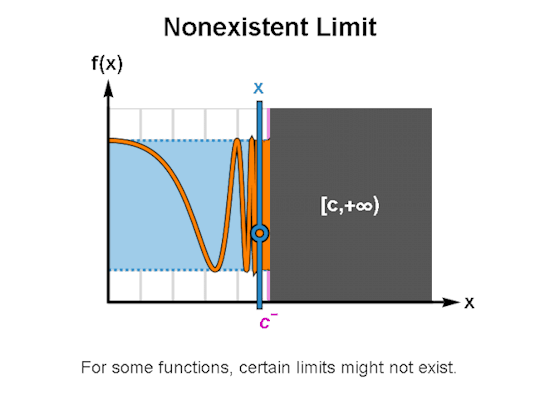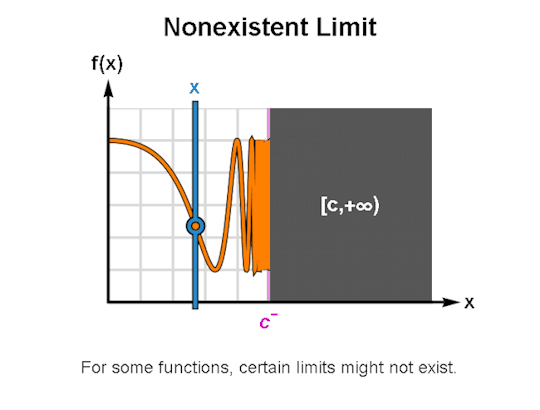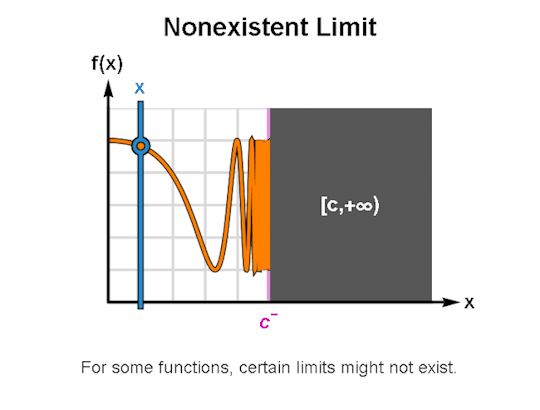
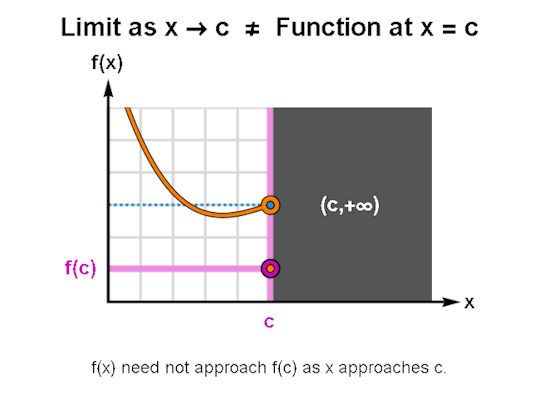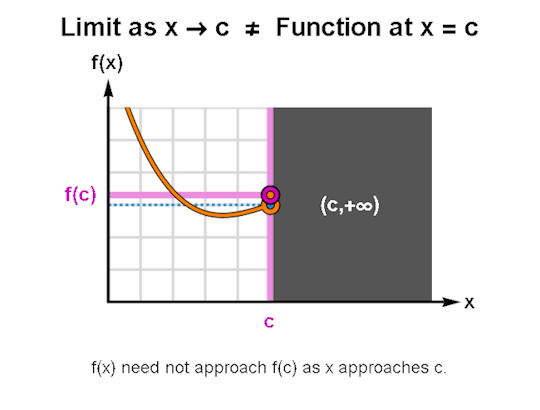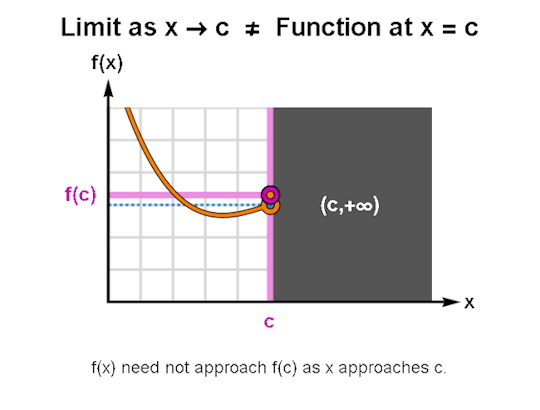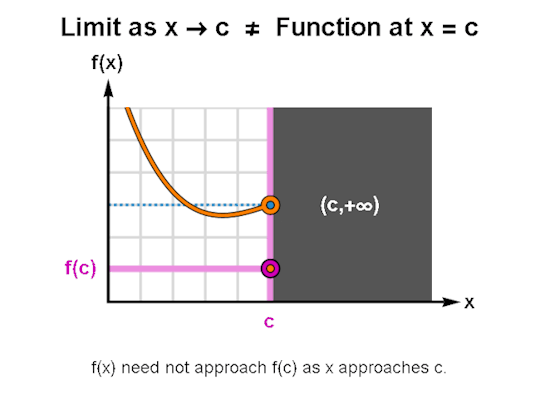
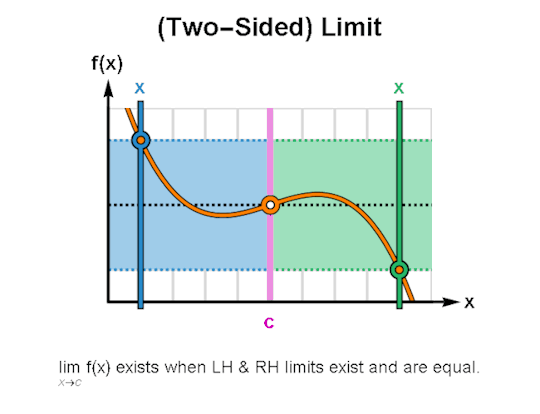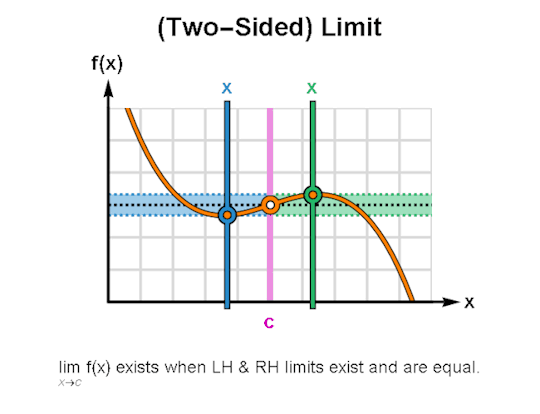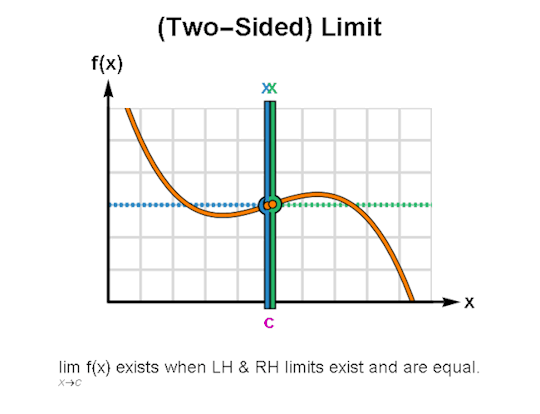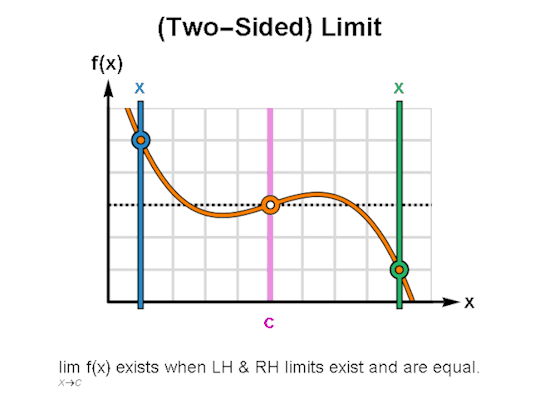
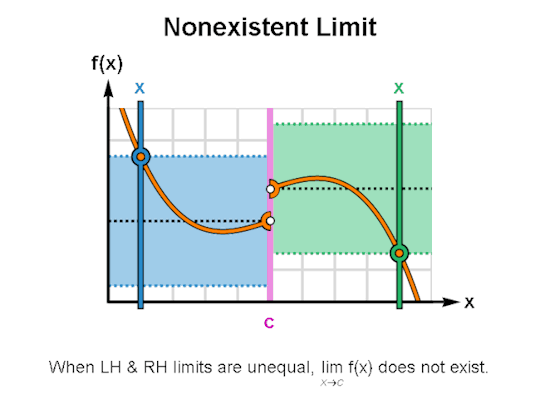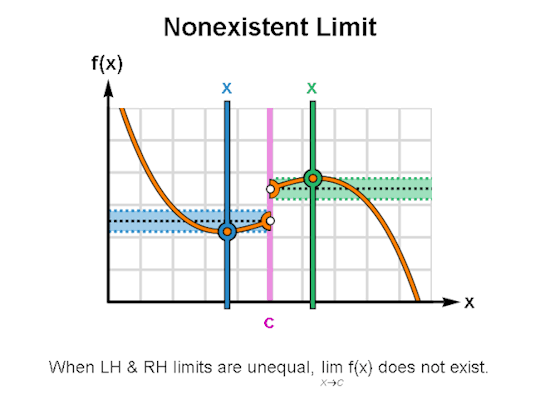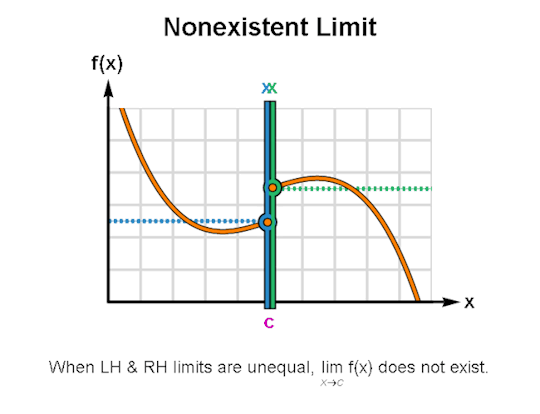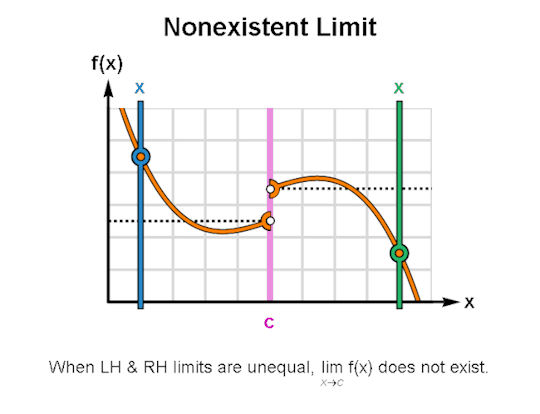
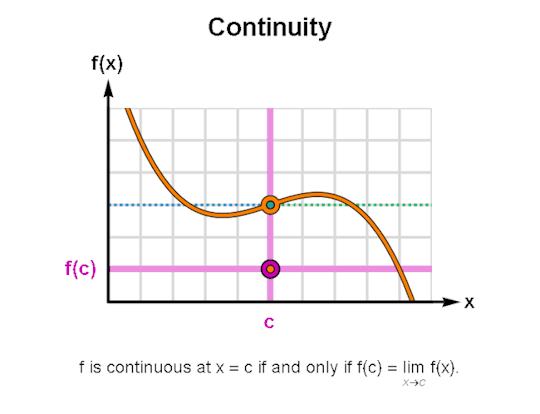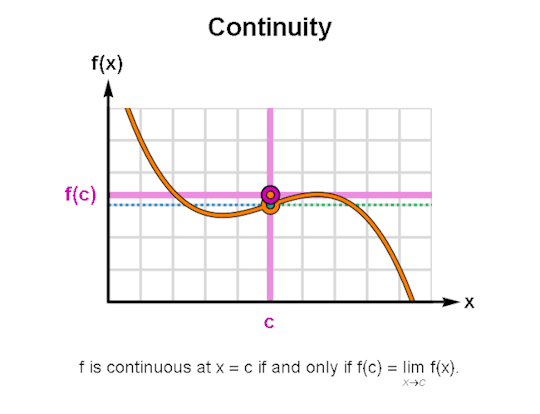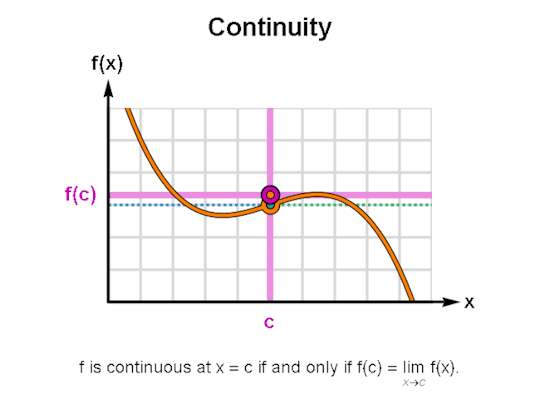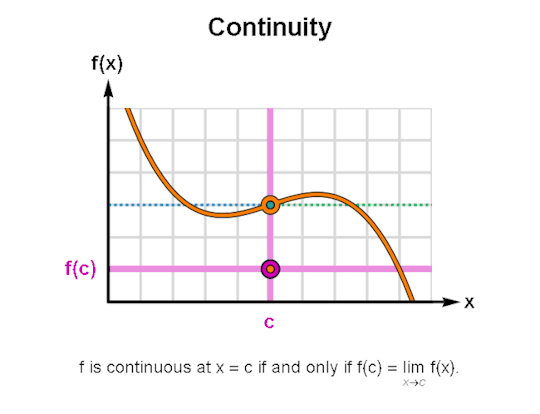
LIMITS & CONTINUITY

When learning calculus, a common first step is learning how to describe the behavior of functions, for which limits & continuity form a particularly important foundation. The above are GIFs I’ve made in Mathematica related to these topics.

I’ve been making these during breaks between writing sessions and they’ve been a lot of fun to create. If there are any other topics for which you’d like GIFs, let me know, and I might just do so. As always, I’m wishing you the best!

GIF descriptions below the break.

Keep reading

[mathwithicecream]

A deformation retract is just a retract that remembers where it came from.

[mathwithicecream]

where’s the tex extension that takes a proof and randomly premutes all the variables so that it’s still correct but completely unreadable

[mathwithicecream]

An Intuitive Introduction to the Homology of Spaces

For almost two years, I’ve been skating by, saying “I don’t want to explain homology right now, homology is complicated, ask me later.”.

Later has come, folks. This is the first post of a seven-part sequence dedicated to shining light on this beautiful, mysterious beast. (1 2 3 4 5 6 7)

For what it’s worth, I know I kind of did this already; way back on Day 6. But the explanation I gave then was half-assed and I knew it. We’re going to do it again, and we’re going to do it right this time: actually comprehensible, geometrically motivated, technically clean, and reasonably paced.

——

If you ask the internet what homology is “about”, you get a wide variety of answers, but eventually a theme develops:

How many holes does a doughnut have?

Roughly speaking, homology groups count and collate holes in a space. [emphasis in original]

[In nice cases] homology is counting the spheres used to construct the space

So, we have 1-dimensional loops, and we count the number of `distinct’ loops which wind round the holes, if any [to get the first homology group]

Basically, the rank of the $n$-th dimensional homology group is the number of $n$-dimensional “holes” the space has.

So, seems to be, something about holes, and maybe loops and spheres. So far, so good.

The last explanation I’ll give is the one furnished by Wikipedia. It has a delightfully intuitive explanation of why this simple-sounding task is so devilishly complicated:

The original motivation for defining homology groups was the observation that two shapes can be distinguished by examining their holes. […] However, because a hole is “not there”, it is not immediately obvious how to define a hole or how to distinguish different kinds of holes.

The point is, we are trying to describe features of the shape that seemingly don’t exist, from the shape’s point of view. Put another way, we are asking homology groups to resolve a much harder analogue of the Flat Earth conundrum. How do we know that the Earth is sphere-ish, instead of flat? Apocryphal stories suggest that the first clue was that ships would disappear over the horizon gradually, the bow before the mast, which suggest some sort of curvature. Of course, the fact was known much earlier: the Greeks, at least, had given it some rigorous consideration, and one story tells of a discrepancy between angles in noontime shadows.

Suppose that we were to get rid of these conveniences. Perhaps the Earth were much, much larger than it actually is, so that ships would disappear into the mist before over the horizon. Moreover, perhaps the entire surface of the planet were completely featureless, so there were no landmarks by which we could orient ourselves. How might we solve the problem now? Probably it’s not even obvious that we can solve the problem now!

Why is this the same as the problem of finding a hole? Well, in this case, if we did suspect we were living on a spherical Earth, we would be looking for the hollow inside of a sphere; what we might call a “two-dimensional” hole. (Of course, the earth isn’t hollow inside. But it might as well be for the purposes of the problem, since the surface is all we really care about: most of us live and die fairly close to it.)

[ By the way: this is not such a contrived scenario. Cosmology now faces a similar question: to determine the shape of the universe. The universe is of course very large, and while it is not completely featureless, there is a huge amount of empty space between any two objects of interest, so landmarks are hard to come by. ]

The inherent difficulty of the task means that we shouldn’t expect good definitions to be simple. Despite these technical troubles, there is still an “intuitive core” which explains how homology groups (technically defined) manage to observe holes in the shape using only data from the shape itself. For the rest of this series, we will be delving into that core.

——

Before we go further in the sequence, I would like to make a technical comment: there are lots and lots of different kinds of homologies. You can essentially always ask “excuse me, which homology?” whenever anyone starts talking about homology. (Fair warning: if you actually do this, you won’t sound intelligent; you’ll sound like an obnoxious pedant.)

For this sequence, “homology” will be an abbreviation for cellular $\mathbf{\Bbb{F}_2}$ (non-reduced) homology. I will ignore almost all of those words to tell you what the “$\mathbf 2$” means. In homological definitions, there are lots of tedious minus signs that get thrown in all over the place. Unfortunately, determining when they show up, and when they don’t, is rather subtle. The 2 in the subscript means that we are “working in characteristic 2”, which means that $1=-1$. This may seem strange, but one way to think of it is that things are either “there” or “not”; it doesn’t make sense to “be there twice”. Another perspective: you can count for nothing, or you can count for something, but nobody counts for more than anyone else.

[ Post 1 ] [ Next ]

——

[ For the experts: we will never explicitly give a cellular decomposition of our spaces, so the pictures will look rather singular. This is of course not an issue since we can just imagine a very fine mesh, constructed “just so” so that the pictures will actually be chains. However, I’m avoiding singular language because I want to be able to talk about dimension in an intuitive sense, a luxury not afforded by singular chains. ]