middlering

[middlering]

Mathematicians will literally fit an infinite plane on a sphere with radius=1 and then look you in the eye and deny being wizards:

@awizardmostkitty what do you think of this evil sorcery?

[middlering]

[middlering]

So what's up with dividing by zero anyways - a ramble on algebraic structures

Most everyone in the world (at least in theory) knows how to add, subtract, multiply, and divide numbers. You can always add two numbers, subtract two numbers, and multiply two numbers. But you must **never** divide by zero... or something along those lines. There's often a line of logic that leads to dividing by zero leading to "infinity," whatever infinity means, unless you're doing 0/0, whatever that means either. Clearly this is a problem! We can't have such inconsistencies in our fundamental operations! Why aren't our top mathematicians working on this?

So, that might be a bit of an exaggeration: division by zero isn't really a problem at all and is, for all intents and purposes fairly well understood, but to see why we'll have to take a crash course through algebra (the field of math, not the grade school version). Sorry for those of y'all who have seen fields and projective space before, not much to gain out of this one.

Part I: In the beginning, we had a Set.

As is true with most things in math, the only structure we start with is a set. A set isn't useful for much; all we can do with a single set is say what elements are and aren't in the set. Once you have more than one set, you start getting interesting things like unions or intersections or functions or Cartesian products, but none of those are _really_ that useful (or at least necessary) for understanding algebraic structures at the level we need, so a single set is what we start with and a single set there will be. The story then goes as follows: on the first day the lord said "Let there be an operation!" and it was so. If you want to be a bit of a nerd, a (binary) operation on a set A is formally a map * : A x A -> A, but for our purposes we just need to know that it matches the standard operations most people know (i.e. addition, subtraction, multiplication, but not division) in that for any two numbers a and b, we can do a * b and get another number. Of course, once again this is not very helpful on its own, and so we need to impose some more conditions on this operation for it to be useful for us. Not to worry though, these conditions are almost always ones you know well, if not by name, and come rather intuitively.

The first structure we'll discuss is that of a monoid: a set with an operation that is associative and has an identity. Associativity simply means that (a * b) * c = a * (b * c), and an identity simply means that we have some special element e such that a * e = e * a = a. For two simple examples and one nonexample, we have the natural numbers (with 0) under addition is a monoid: 0 + a *= *a *+ 0 = *a, and any two natural numbers add to another natural number; the integers under multiplication is a monoid: 1 * a = a * 1 = a, and any two integers multiply to another integer; and the integers under subtraction is not a monoid, since subtraction is not associative (a - (b - c) =/= (a-b) - c). In both of these examples, the operation is commutative: in other words, a * b = b * a for every a and b. There are plenty of examples of operations that are not commutative, matrix multiplication or function composition probably being the most famous, but for the structures we're going to be interested in later operations are almost always commutative, so we can just assume that from the start.

Of course, you might wonder where subtraction comes from, if it doesn't fit into a monoid structure (and in particular isn't associative). Not to worry! We can simply view subtraction as another type of addition, and our problems go away. In particular, we add the condition that for every a, we have an inverse element a⁻ ¹ (or -a if our operation is addition) such that a * a⁻ ¹ = a⁻ ¹ * a = e. For fans of universal algebra, just as a binary operation can be thought of as a function, the inverse can be thought of as a function i : A -> A that sends each element to its inverse. This forms a structure we know as a group. While none of the above examples form a group, one of them can be naturally extended to a group: if we simply add negative whole numbers to natural numbers, we get the group of integers over addition, where for any integer a, we have its inverse -a where a + -a = 0. In particular, the subtraction a - b is just a + -b = -b + a, where -b is the additive inverse of b. As we will soon see, division can also be thought of in a similar way, where a/b = a * /b = /b * a where /b is the multiplicative inverse of b. As a side note, the examples above are very specific types of monoids and groups which turn out to be quite far from the general ideas that monoids and groups are trying to encapsulate. Monoids show up often in computer science as they're a good model for describing how a list of commands affects a computer, and groups are better thought of as encapsulating symmetries of an object (think of the ways you can rotate and reflect a square or a cube).

Part II: So imagine if instead of one operation, we have... two...

If you've ever taken introductory algebra, you've probably never heard of monoids and only done groups. This is partially because monoids are much less mathematically interesting than groups are and partially because monoids are just not as useful when thinking about other things. For the purposes of this post, however, the logical steps from Set -> Monoid -> Group are surprisingly similar to the steps Group -> Ring -> Field, so I've chosen to include it regardless.

Just as we started from a set and added an operation to make a monoid, here we start from an additive group (i.e. a group where the operation is addition) and add another operation, namely multiplication, that acts on the elements of the group. Just like in the monoid, we will impose the condition that multiplication is associative and has an identity, namely 1, but we also impose the condition that multiplication meshes nicely with addition in what you probably know as the distributive properties. What we end up with is a ring, something like the integers, where you can add, subtract, and multiply, but not necessarily divide (for example, 2 doesn't have a multiplicative inverse in the integers, as a * 2 = 1 has no solutions). Similarly, when we add in multiplicative inverses to every nonzero element, we get a field, something like the rational numbers or the real numbers, where we can now divide by every nonzero number. In other words, a ring is an additive group with a multiplicative monoid, and a field is an additive group with a subset that is a multiplicative group (in particular the subset that is everything except zero). For those who want to be pedantic, multiplication in a ring doesn't have to be commutative, but addition is, and both addition and multiplication are commutative in a field. A full list of the conditions we impose on the operations of a monoid, group, ring, and field can be found here).

So why can't we have a multiplicative inverse to 0 in a field? As it turns out, this is because 0 * a = 0 for every a, so nothing times 0 gets you to 1. There is technically a structure you can have if 0 = 1, but it turns out there's only the one single element 0 in that structure and nothing interesting happens, so generally fields specifically don't allow 0 = 1. Then, what if instead we relaxed the condition that 0 * a = 0? Similarly, it turns out that this isn't one of the fundamental conditions on multiplication, but rather arises from the other properties (a simple proof is a * 0 = a * (0 + 0) = a * 0 + a * 0 implies 0 = a * 0 - a * 0 = a * 0 + a * 0 - a * 0 = a * 0). If we were to relax this condition, then we lose some of the other nice properties that we built up. This will be a recurring theme throughout the rest of this post, so be wary.

Part III. We can't have everything we want in life.

While all the structures so far have been purely algebraic and purely algebraically motivated, the simplest way to start dividing by zero is actually "geometric," with several different ways of constructing the same space. The construction we'll use is as follows: take any field, particularly the real numbers or the complex numbers. We can always take the cartesian product of a field K with itself to form what's called affine space K^2, which is the set of ordered pairs (a,b) for a, b in K. As a side note, the product of groups, rings, or fields has a natural definition of addition or whatever the underlying group operation is by doing it componentwise, i.e. (a,b) * (c,d) = (a * c, b * d), but our operations will not coincide with this, as you'll see soon. This affine space is a plane - in fact, when we do this to the real numbers, we get the Cartesian plane - within which we can construct lines, some of which we get by considering the set of points (x, y) satisfying the familiar equation y = mx + b for some 'slope' m and 'intercept' b. In particular, we want to characterize all the lines through the origin. This gives us all the lines of the form y = mx, as well as one additional line x = 0. This is the basic construction of what we call the projective line, a space characterizing all the lines through the origin of affine 2-space. The geometric picture of this space is actually a circle: the bottom point representing the number 0; the left and right halves representing negative and positive numbers, repsectively; and the top point representing the number "infinity."

There are a few ways of describing points on the projective line. The formal way of doing so is by using what are called homogenous coordinates. In other words, for any nonzero point (a,b) in affine space, it is surely true that we can find a line through the origin and (a,b). In particular, if a is not zero, then this line takes the form y = (b/a) x where the slope is b/a. Furthermore, any two points (a,b) and (c,d) can actually sit on the same line, in particular whenever c = ka and d = kb for some number k. Thus, we can define homogenous coordinates as the set of points [a : b] for a, b in our field where [a : b] = [ka : kb] by definition, and the point [0 : 0] is not allowed as it doesn't specify any particular line (after all, every line passes through the origin). As is alluded to above, however, this means that whenever a =/= 0, we can take k = 1/a to get [a : b] = [1 : b/a], in other words characterizing each line by its slope. Furthermore, whenever a = 0, we can take k = 1/b to get [0 : b] = [0 : 1]. In other words, the projective line is, as we informally stated above, equivalent to the set of slopes of lines through the origin plus one other point representing the vertical line, the point at "infinity." Since slopes are just numbers in a field, we can add, subtract, multiply, and divide them as we normally do with one exception: the slope of the lines containing [a : b] for any a =/= 0 is b/a, so clearly the line with infinite slope consisting of points [0 : b] implies that b/0 should be infinity. Voila! We can divide by zero now, right? Well... there are two loose ends to tie down. The first is what infinity actually means in this case, since it is among the most misunderstood concepts in mathematics. Normally, when people bandy about phrases such as "infinity isn't a number, just a concept" or "some infinities are different from others" they are usually wrong (but well meaning) and also talking about a different kind of infinity, the ones that arise from cardinalities. Everything in math depends on the context in which it lies, and infinity is no different. You may have heard of the cardinal infinity, the subject of Hilbert's Hotel, describing the size of sets and written primarily with aleph numbers. Similarly, you may also have heard of the ordinal infinity, describing the "place" in the number line greater than any natural number. Our infinity is neither of these: it is to some extent an infinity by name only, called such primarily to take advantage of the intuition behind dividing by zero. It's not "greater" than any other number (in fact, the normal ordering of an ordered fields such as the real numbers breaks down on the projective line), and this is a consequence of the fact that if you make increasingly negative and increasingly positive slopes you end up near the same place: a vertical line. In other words, "negative infinity" and "positive infinity" are the same infinity.

The second loose end is that defining our operations this way is actually somewhat algebraically unsound, at least with respect to the way we think about operations in groups, rings, and fields. As mentioned above, the operation of addition can be lifted to affine space as (a,b) + (c,d) = (a+c,b+d). However, this same operation can't really be used for homogenous coordinates, since [1, 0] = [2, 0] as they lie on the same line (the line with slope 0), but [1, 0] + [1, 1] = [2, 1] while [2, 0] + [1, 1] = [3, 1], and [2, 1] and [3, 1] are not the same line, as they have slopes 1/2 and 1/3, respectively. Dividing by zero isn't even needed to get weirdness here. Luckily, we can simply define new operations by taking inspiration from fractions: b/a + d/c = (bc + ad)/ac, so we can let [a : b] + [c : d] equal [ac : bc + ad] (remembering that homogenous coordinates do to some extent just represent the slope). Luckily, multiplication still works nicely, so we have [a : b] * [c : d] = [ac : bd]. Unluckily, with these definitions, we no longer get a field. In particular, we don't even have an additive group anymore: [a : b] + [0 : 1] = [0 : a] = [0 : 1], so anything plus infinity is still infinity. In other words, infinity doesn't have an additive inverse. Furthermore, despite ostensibly defining infinity as 1/0, the multiplicative inverse of 0, we have that [1 : 0] * [0 : 1] = [0 : 0], by our rules, which isn't defined. Thus, 0 still doesn't have a multiplicative inverse and 0/0 still doesn't exist. It seems like we still haven't really figured out how to divide by zero, after all this. (Once again, if you want to read up on the projective line, which is a special case of projective space, which is a special case of the Grassmannian, in more depth.)

Part IV: I would say wheels would solve all our problems, if not for the fact that they just make more problems.

At this point, to really divide by zero properly, we're going to need to bite the bullet and change what dividing really means. Just as we can think of subtraction as adding the additive inverse (i.e. a - b = a + -b where -b was a number), we can start thinking of division as just multiplying by... something, i.e. a/b = a * /b, where /b is something vaguely related to the multiplicative inverse. We can already start doing this in the projective line, where we can define /[a : b] = [b : a], and it works nicely as [a : b] * [b : a] = [ab : ab] = [1 : 1] whenever neither a nor b is zero. This lets us rigorize the statements 1/infinity = 0, infinity/0 = infinity, and 0/infinity = 0, but doesn't really help us do 0/0 or infinity/infinity. Furthermore, note that because 0/0 =/= 1, /[a : b] isn't really the multiplicative identity of [a : b], it's just the closest we can get.

Enter the wheel! If 0/0 is undefined, then we can simply... define it. It worked so nicely for adding in infinity, after all - the picture of the point we added for infinity is taking a line and curling it up into a circle, and I like circles! Surely adding another point for 0/0 would be able to provide a nice insight just as turning a line into the projective line did for us.

So here's how you make a wheel:

You take a circle.

You add a point in the middle.

Yeah that's it. The new point, usually denoted by ⊥, is specifically defined as 0/0, and really just doesn't do anything else. Just like for infinity, we still have that a + ⊥ = ⊥ and a * ⊥ = ⊥ for all a (including infinity and ⊥). It doesn't fit into an order, it doesn't fit in topologically, it is algebraically inert both with respect to addition and multiplication. It is the algebraic formalization of the structure that gives you NaN whenever you fuck up in a calculator and the one use of it both inside and outside mathematics is that it lets you be pedantic whenever your elementary school teacher says "you can't divide by zero" because you can go "yeah you can it's just ⊥ because i've been secretly embedding all my real numbers into a wheel this whole time" (supposing you can even pronounce that).

Part V: So what was the point of all this anyways

The wheel is charming to me because it is one of the structures in mathematics where you can tell someone just asked a question of "what if this was true," built some space where it was, and just started toying with it to see what happens. It's a very human and very beautiful thing to see someone go against conventional knowledge and ask "what breaks when you allow 0/0" even if conventional knowledge does tend to be right most of the time. In this sense, perhaps the uselessness of the wheel is the point, that even despite how little ⊥ does from a mathematical lens, some people still took the time to axiomatize this system, to find a list of conditions that were both consistent and sufficient to describe a wheel, and genuinely do actual work seeing how it fits in within the universe of algebraic structures that it stays in.

While a wheel may not be used for much (it might be describable in universal algebra while a field isn't, though I'm not too well versed in universal algebra so I'm not actually entirely sure), every other structure discussed above is genuinely well studied and applicable within many fields inside and outside of math. For more viewpoints on what the projective line (and in general the projective sphere) is used for, some keywords to help you on your way are compactification of a set if you care about the topological lens, the real projective line or the Riemann Sphere if you care more about the analysis side, or honestly the entirety of classical algebraic geometry if that's your thing.

Another structure that might be interesting to look at is the general case of common meadows, an algebraic structure (M, 0, 1, +, -, *, /) where the condition of / being involutive (i.e. /(/x) is not always x) is relaxed, unlike a wheel where it is always involutive. Note that these structures are called meadows because the base structure they worked on is a field (get it? not our best work I promise mathematicians are funnier than this). These structures are at the very least probably more interesting than wheels, though I haven't checked them out in any amount of detail either so who knows, perhaps there isn't much of substance there either.

[middlering]

it's not mentioned in the song but in the corner of the piano man bar there is a mouse hole and inside that hole is a smaller replica of the bar staffed and patronized by mice who perfectly mirror all of the characters and they all say squeak us a song you're the piano mouse and mouse what are you doing here while they put cheese in his tiny jar

[middlering]

But between the drinks and subtle things The holes in my apologies You know I'm trying hard to take it back

So if by the time the bar closes And you feel like falling down I'll carry you home

[middlering]

I spent too much time on this…

Define the natural numbers N By axiomatizing some rules Putting logic in arithmetic Which you learned when you started in school

Now first N must have at least one element (We'll have to assume this first part) It's called zero by some, Peano chose to use 1 A number from which we can start

La la la di di da, la la di di da, da dum…

Sing us a song, you're the Peano Man Sing us a song tonight Well x ∈ the mood for a melody ∀x∈N And x = feeling alright

Now S : N -> N is a special map The successor function, it's called It's injective and closed and he already knows That S(n) = 0 must be false

Say a set contains 0 as well as all The successors of each of its n, We can show by means of this inductive trick That this set's just equal to N

Oh la la la di di da, la la di di da, da dum…

Now + is defined by the following: A number plus 0 stays the same, Adding a and S(b) gives us S(a+b), And commutativity is plain

And the multiplication is similar As a number times 0 is 0, a • S(b) = a + (a • b) so The distributive property holds

And I say…

Sing us a song, you're the Peano Man Sing us a song tonight Well x ∈ the mood for a melody ∀x∈N And x = feeling alright

a is less than or equal to b in N If the property here is agreed: a+c=b for some natural c And that's all the relations we need

And the Peano axioms, categorical But their consistency's still abstruse For despite Gödel's truth, Gerhard Gentzen has proved It depends on the system you use!

La la la di di da, la la di di da, da dum…

Sing us a song, you're the Peano Man Sing us a song tonight Well x ∈ the mood for a melody ∀x∈N And x = feeling alright

Idea: A Piano Man parody that is about the Peano Axioms.

Peano Man

[middlering]

[middlering]

Why do we use the symbol for partial derivatives as the symbol for boundaries of manifolds?

[middlering]

And God said, "Behold! I have created the fourth primordial force: the weak interaction!"

And the angels all clapped and nodded politely, and there was a long silence; and finally Verchiel, the Angel of Grace, spoke up and asked, "Er, what exactly does it do, O Fashioner?"

And God said, "What do you mean, 'what does it do?' It's the fourth fundamental force of the universe."

And Verchiel said, "You mentioned that. Um. But it's just that the other three sort of have a brand, you know? Gravity helps build large-scale structures, acts over vast cosmic distances, shapes time and space. The strong force is secret, hidden, binding together quarks and all that. Electromagnetism, very cool stuff, somewhere in between. We're all big fans of the whole magnetic monopole double bluff, very clever. But, er. What does this 'weak interaction' do?"

And God said, "It mediates radioactive decay. Sort of."

And Verchiel said, "Radioactive decay? All radioactive decay?"

And God said, "No. Just some kinds."

And Zephaniel, the Chief of the Ishim spoke, and he said, "A whole independent force just to mediate some kinds of radioactive decay?"

And God said, "Well. Not totally independent. Technically it's related to electromagnetism."

And Zephaniel said, "Wait, it's not even a real force?"

And God said, "It's totally a real force. It's just that it's one aspect of a combined electromagnetic and weak force. An electro-weak force, if you will."

And Metatron, the Celestial Scribe, scratched his head at this, but said nothing.

And Cambiel, the Angel of Transformation, said, "Maybe you can walk us through it from the top."

And God Sighed an immense Sigh, and said, "All right, fine.

"So the way it works is that all of space and time is permeated by a field that has imaginary mass."

And Cambiel said, "Imaginary mass, O Generous Provider?"

And God said, "Yes, imaginary mass. It's tachyonic, d'you see?"

And Sarathiel, the Angel of Discipline, said, "Wait a minute, I thought we agreed nothing was going to travel faster than light? All that 'c' business and the whole Lorentz transformation thing. What's happening with that?"

And God said, "Let me finish. The field is tachyonic. The particles in the field all move slower than light."

And Sarathiel had to think about this for a second.

And God said, "The point is, a field with imaginary mass has a non-zero vacuum expectation value."

And this really gave Sarathiel trouble, since he had never been very good at math.

And God, seeing this, went back to explain. "Most fields, like the electromagnetic field, have no effect when they are at their lowest energy state. It's like they're not there at all. If you give a field imaginary mass, then it vanishes only when it's at a very high energy state, and at a low energy state, it has a nonzero value everywhere."

And Sarathiel nodded, but he was confused, because he didn't understand why God would create such a thing.

But Verchiel thought he saw where God was going with this, and he was amazed.

"Truly, you are cunning beyond measure, O Only One Certainly Sound and Genuine in Truth! Only now do I understand your design! For in order to make the universe homogenous and isotropic, it is necessary that all large-scale fluctuations in temperature and mass must be evened out early in the history of the cosmos; and therefore, you have designed a field which will rapidly expand space after the Big Bang, many orders of magnitude in brief moments, and then swiftly and spontaneously decay as it gives up the energy it began with, giving rise to radiation and particles of all kinds as it does, which will condense into the material universe! It is a wonder to behold."

And God said, "What? No. I mean I did, but this isn't the inflaton field I'm talking about. This is something else."

And Verchiel said, "Wait, it's not?"

And God said, "No, I'm going to use a different field to drive cosmic inflation. The properties of this field are totally different."

And now Verchiel was also confused, and lapsed into silence.

And God said, "Like I was saying, this field is a scalar field with imaginary mass, and it does spontaneously decay to a ground state with a non-zero value. But it's not the inflaton field. Instead it combines with the W1, W2, W3, and B bosons."

And Metatron began to flip back through the pages of the Heavenly Record trying to figure out where he'd lost the thread.

And Zephaniel said, "The what bosons?"

And God said, "The W1, W2, W3, and B bosons. I'm sure I mentioned them. You know, the massless bosons?"

And Zephaniel said, "I'm pretty sure we only talked about the W+, W-, and Z0 bosons. All of which you said were going to have mass, O Owner of All Sovereignty."

And God said, "Yes, but this is how they get them, you see. Once this field acquires a nonzero value everywhere, the massless bosons interact with it and get mass. Well, some of them do. They turn into the W+, W-, and Z0 boson. And the photon."

And Zephaniel said, "…and the photon, O Accepter of Invocation?"

And God said, "Well, I did say I was going to unify the electromagnetic force and the weak interaction, didn't I? This is how. Above the critical temperature--right now I'm thinking 10^15 K, but I'm open to feedback on that one--electromagnetism and the weak force act as a single unifying force. Below that temperature, the field gets a nonzero value, you get three massive bosons to mediate the weak interaction, and the photon pops out seperately."

And Zephaniel said, "That seems… a bit overly complicated, doesn't it, O Reinstater Who Brings Back All?"

And God said, "No, it's exactly what we need. Look, that way the W and Z bosons have something to do, but the weak interaction still only travels short distances. Gravity is still the star of the show on cosmic scales, as it were. But now quarks and leptons can swap their flavor!"

And Zephaniel said, rather weakly, "Their… flavor, O Source of Good?"

And God said, "It's this new quantum number I'm trying out, to give the three generations of matter more unique identities."

And Cambiel said, "Three generations of matter? Now I'm really confused."

And God said, "I'm sure I mentioned this. You've got the lightest quarks and leptons, and then two heavier versions of each that can decay into the lighter versions."

And Cambiel said, "What do they do? New kinds of chemistry, is it?"

And God said, "Well, no. Mostly they just decay in a couple microseconds. Or even faster."

And Zephaniel began to rub his temples, and Cambiel sniffed.

And Cambiel said, "This all seems a bit ad hoc to me. Not really the stuff of an elegant and obviously ordered Creation. Why not have four generations of matter? Why not a trillion?"

And God began to grow irritable, and said, "Well, that's not really up to you, now is it? We're going to have three generations of matter, and the electroweak force, and that's that!"

And Zephaniel said, "As long as we are unifying fundamental forces, perhaps we could somehow also unify the electroweak interaction with the strong interaction, or even gravity."

And God hesitated saying, "Well, I haven't decided about that yet. I'm not sure I want gravity to be quantized, you know? Seems to take some of the geometric elegance out of general relativity."

And now it was Zephaniel's turn to sigh, and he bowed his head. "As you wish, O Possessor of Authority of Decisions and Judgement."

[middlering]

After the math pope, we have a math president

From the Wiki page of Nicușor Dan, the new president of Romania:

He won first prizes in the International Mathematical Olympiads in 1987 and 1988 with perfect scores.[3] Dan moved to Bucharest at the age of 18 and began studying mathematics at the University of Bucharest.[4] In 1992, he moved to France to continue studying mathematics: he followed the courses of the École Normale Supérieure, one of the most prestigious French grandes écoles, where he gained a master's degree. In 1998 Dan completed a PhD in mathematics at Paris 13 University, with thesis "Courants de Green et prolongement méromorphe" written under the direction of Christophe Soulé and Daniel Barsky [de].[5][6]

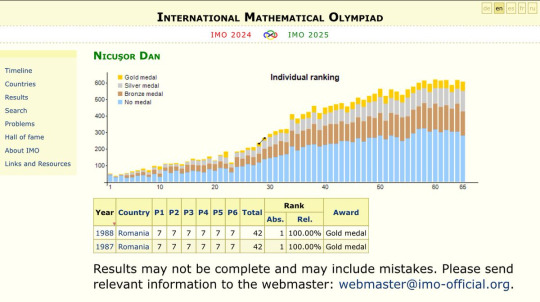
Dan's 1988 gold medal also means he was one of eleven contestants to get full marks on the infamous Problem 6, a question so difficult that nobody on the IMO problem committee could solve it.

His personal website lists his primary area of research as Arakelov geometry, a method of studying Diophantine equations from a geometric point of view.

His thesis, in the same field.

His arXiv.

[middlering]

#holding out hope the new documentary confirms my theory that 'died in september' refers to the suicide attempts occurring in september 1970

Having it on the record one way or the other would be everything.

The other thing that gets me about the lyrics (and I also put this into my giant Billy Joel essay) is "Unsung songs show my direction" because Walter Everett once compared the song's composition to Henry Mancini and André Propp and in 1971 both of them had just written instrumental songs ("A Time for Us" and "Love is Blue") that went to the top of the charts. So that line is already meta for the likely inspirations behind "Silver Seas" but then he removed the lyrics and added another self-referential layer because now that lyric refers to "Nocturne" itself too.

Once I lived You might remember Born in May Died in September

[middlering]

physics is scary what the hell is the Riemann zeta function doing in the equation for the critical temperature of a Bose-Einstein condensate

[middlering]

So I recently stumbled on the Wikipedia article for the Grothendieck-Riemann-Roch theorem, which is an algebraic geometry thing that I'll hopefully learn some day once I actually have the prerequisite knowledge =w= But at the top of the article was this letter, which I thought was a wild thing to have at the top of a Wikipedia article about a niche abstract math thing - here's a translation:

Witches' Kitchen 1971 Riemann-Rochian Theorem: the latest craze*: the diagram

is commutatif**! To give this statement about f: X->Y some approximative meaning, I had to abuse the listeners' patience for nearly two hours. In black and white (in Springer's Lecture Notes) it seems like it will take up to about 400, 500 pages. A gripping example of how our thirst for knowledge and discovery indulges itself more and more in a(n il?)logical delirium far removed from life, while life itself is going to hell in thousandfold ways - and is threatened with absolute annihilation. High time to change our course! (6.12.1971) Alexander Grothendiek

* "der letzte Schrei" is a reasonably common German idiom meaning "the latest craze", but here it could alternatively be translated non-idiomatically as something like "the last cry". I think its more fun to imagine he means the idiom. ** I'm assuming this is a weird old-timey spelling probably taken from french but googling it I can find no examples of anybody using this spelling in German besides this letter

Note that this is 20 years before all of this happens:

[middlering]

Blatantly Partisan Party Review XV (federal 2025): Katter’s Australian Party

Running where: QLD. The party is contesting three House divisions: Bob Katter himself for Kennedy, plus candidates in Herbert and Leichhardt, while in the Senate, a candidate is second on a joint ticket with Rennick First for Group G

Prior reviews: federal 2013, federal 2016, federal 2019, federal 2022

What I said before: “For those of us on the left, KAP has a few things to like and a lot to detest.” (federal 2022)

What I think this year: I’ve already covered a bunch of “dontcha know who I am?” cult-of-personality parties, and here is perhaps the most larger-than-life personality of the Australian political scene: the North Queenslander in the big hat, the man who would let a thousand blossoms bloom, part of the parliamentary furniture itself, the one and only Bob Katter.

Now, Bob is a character but he's consistent one, so instead of reprising the greatest hits that I've featured before, I thought I would present you with some history to contextualise him and his electorate. Katter’s seat of Kennedy is a vast one. It stretches from the Coral Sea coast between Cairns and Townsville, across the Great Dividing Range, and through Outback towns such as Charters Towers, Hughenden, and Cloncurry out to Mount Isa, across to the NT border, and up to the shores of the Gulf of Carpentaria. Bob Katter has seemingly stomped the length and breadth of it to become an enduringly popular local member. Although Kennedy is one of the original 65 electorates from Federation in 1901, Katter is remarkably just the seventh person to hold it.

Kennedy was in Labor hands from 1929 to 1966 while Darby Riordan and then his nephew Bill held the seat, but for the last 59 years it has been a family business for the other side of politics:, a Katter has represented Kennedy for all but 3 years. Bob’s father, Bob Katter Sr, won it for the Country Party (later renamed the Nationals) and held it from 1966 until his death in 1990, while the young fella learned the family business as a state MP from 1974. Bob Jr served as a cabinet minister from 1983 under another larger-than-life Queensland pollie, Joh Bjelke-Petersen, and in August 1989, Sir Joh unsuccessfully endorsed Katter as his successor as premier. Instead, Bob Jr had an annus horribilis: he went into opposition at the December 1989 Queensland state election, his dad died days before the March 1990 federal election, and Kennedy fell to Labor. The new MP, Rob Hulls, however, only got one term representing this sprawling constituency (and yes, Victorian readers with long memories, that is the Rob Hulls, deputy premier to John Brumby in 2007–10; quite the change of scenery!).

Katter shifted to federal parliament at the 1993 election, winning back the seat of dear old dad, and he has held Kennedy ever since. In 2001 he left the Nationals to sit as an independent: he disagreed with the rise of neoliberal economics (good!) and with some of the Coalition’s more socially liberal policies (bad! especially as the Coalition is uhh not very socially liberal!). In 2011, he founded Katter’s Australian Party, which met with very little success outside Queensland at the 2013 and 2016 federal elections and has since focused on winning seats in North Queensland. It really ought to be called Katter's North Queensland Party.

Bob’s son Robbie has been the party leader since 2020, and at state level KAP holds three seats that overlap with the Division of Kennedy. But Bob is the only KAP representative at federal level; ex-One Nation lunatic Fraser Anning briefly joined KAP as a Senator in 2018 but proved to be too barmy even for the Katters. I see little reason to anticipate any change to the party’s representation this year. If you live in Kennedy, you probably know Katter is a strong favourite to retain his seat; if you don’t, I hope the history above helped make this explicable.

What is Bob emphasising in his campaign this year? Well, per the homepage, “KAP = Castle Law”. Yes, their core focus is a fear campaign that “crime in Queensland is out of control” and people have a “right to defend their home against intruders without facing legal consequences”. Look, I spent my teenage years in a conservative Queensland setting where A Current Affair was as serious a source of news as the 7:30 Report, but shooting dead a trespasser in your garden is disproportionate. KAP states that “Under the current law, people must demonstrate they have only used ‘necessary’ force under the ‘reasonable belief’ that the intruder was entering their home to commit a serious crime”. Seems fine to me! But they think that people “cannot always make split-second, measured decisions in moments of crisis”. The existing law as per their own description already accommodates this: a person fiddling with your gate is obviously a different degree of threat to somebody confronting you in your bedroom with a knife, and going out all guns blazing at the former is not "reasonable". KAP's policy is a solution in search of a problem.

Other policies? Still on crime, KAP has a four-step “send ‘em out bush” policy for young offenders that in practice would just make them more resentful. You won’t be surprised to learn that KAP wants harsher sentences in general for youth offending and backs the LNP’s “adult crime = adult time” approach. Turning to energy, KAP want more coal, more gas, and new nuclear. Other infrastructure policies focus mainly on roads and on dams to support agriculture. Unsurprisingly for a party whose largest donors are from the gun lobby, KAP’s approach to firearms is permissive. And maybe one of their odder policies is that “KAP wants flying foxes gone from populated areas” and supports culling them. Did a flying fox steal your dog Bob? Come on man. Three of seven species of flying fox in Australia are listed as vulnerable or endangered.

And, of course, for a party led by a man whose most famous remark is about crocodiles tearing people to pieces in North Queensland, there is a policy that “values human life above crocodiles”. Enjoy. Should this move you, perhaps you might also want to buy an official “let there be a thousand blossoms bloom” shirt. If so, Bob’s got a shop for that. I am not kidding.

Recommendation: Give Katter’s Australian Party a very low preference in the House and a weak or no preference in the Senate.

Website: https://kattersaustralianparty.org.au/

(For the pol nerds: Bob is currently Father of the House, i.e. the longest-serving current MP, but at just over 32 years in office he is not yet in the top ten ever. If the new parliament goes to term and Bob does not retire before the election, he will be either 10th or 11th  on the all-time list depending on the exact day of election. He needs to serve five years from today to get into the top five, 10.5 years to get into the top two, and just shy of twenty years to pass Billy Hughes’ record of 51 years and 213 days. Keep in mind that Bob turns 80 next month. Now, yes, he served 18 years in Queensland’s state parliament, so as of this year he has been in a parliament for half a century, but Billy Hughes served in the NSW parliament for 7 years; to exceed Hughes’ cumulative time, Katter needs to be in office for another 8.7 years)

[middlering]

If your 5 favorite Billy Joel songs were birds what would they be and why

Hmmmmm, that's a really good question that I hadn't thought of before.....let's see:

The Stranger (1977)

I think it'd have to be either a mimicking bird or a brood parasite. So I'm thinking either a Common Cuckoo, a brood parasite:

Or a European Starling, an expert mimic and also an invasive species here in North America:

It's Still Rock and Roll to Me (1980)

This song screams Rock Pigeon, with its stubborness and memory of a better time:

Pressure (1982)

This one has to be a bird that has a really long migration route, so why not the one with the longest, the Arctic Tern:

Lullabye (1994)

This song makes me think of endangered and extinct birds. I think of the last song of the Kauaʻi ʻōʻō, a bird that was formally declared extinct in 2023, but was last heard in 1987:

I also think of the Zebra Finch, often the subject of experiments about communication development, that can involve isolating a baby bird from their parents so they cannot learn their proper song:

Goodnight Saigon (1982)

This makes me think of the Wake Island Rail, which went extinct as a consequence of WW2 (this song is about Vietnam, but I think it can apply to a lot of war):

I also think of Edward's Pheasant, which is believed to be extinct in the wild, in a large part due to the effects of the Vietnam War:

Thank you so much for the question!!!

[middlering]

My favorite genre of self-portrait is cartoonists being bothered by their characters while trying to draw

Bill Watterson – Calvin and Hobbes (1986)

Hergé – Tintin (1947, Tintin Magazine)

Albert Uderzo – Asterix (the cover of Uderzo l'Irreductible (2018), but originally much older)

Jeff Smith – Bone (1993, Bone Holiday Special)

Walt Kelly – Pogo (1950, Maclean's Magazine)

And a bonus:

Berkeley Breathed – Bloom County

[middlering]

how has nobody posted anything about the openly gay republican running for lieutenant governor of virginia who is getting attacked by his party-mates for allegedly reblogging naked men on tumblr