#Expand the Trigonometric Expression sin(pi-x)

[mathandnumberystuff]

How to calculate exact trig values, part 3

11th roots of unity

This is my third post about calculating exact trigonometrical values based on roots of unity. I am giving the examples for prime roots of unity.

My previous post showed that the 7th roots of unity had square roots and cube roots in their formulas, because 7 - 1 = 2*3. Since 11 - 1 = 2*5, the 11th roots of unity will have square roots and 5th roots in their expression, namely, a sum of 4 fifth roots, each of formulas involving the fifth roots of unity.

Before we start, I want to make a correction to something I said earlier. In my last post I stated that a1 + a2 + a3 + r1*(a1 + r1*a2 + r2*a3) + r2*(a1 + r2*a2 + r1*a3) = 3*r1, and a1 + a2 + a3 + r2*(a1 + r1*a2 + r2*a3) + r1*(a1 + r2*a2 + r1*a3) = 3*r2. In fact, the first left-hand expression equals 3*r2 and the second equals 3*r1. This is the corrected expression for the 7th root of unity:

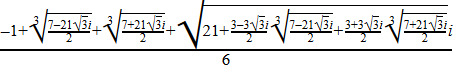
Now on to the current calculation.

Here are the 11th roots of unity:

1, x1, x2, x3, x4, x5, x6, x7, x8, x9, x10

Let’s try to find a power cycle that goes through each 11th root of unity once, except for 1, starting with x1.

Let’s try squaring each term. Since x(n) is just x1^n, and x1^11 = 1, then x(a)*x(b) = x((a + b) mod 11). This is axiom 2 from the first post.

x1, x2, x4, x8, x5, x10, x9, x7, x3, x6, x1...

This gives us a cycle of 10, like we wanted. Now to find each root of unity, we are going to be solving a quadratic equation and a quintic equation. Let’s first find the roots of the equation by summing together every fifth term of the cycle, starting from the first, second, third, and fourth, and fifth terms:

x1 + x10 = a1

x2 + x9 = a2

x4 + x7 = a3

x8 + x3 = a4

x5 + x6 = a5

To find each of these values, we will need to find the following values, where r1, r2, r3, and r4 are the four 5th roots of unity not equal to 1, r1 has a polar angle of 2*pi/5, and r(n) = r1^n:

a1 + a2 + a3 + a4 + a5 = s0

a1 + r1*a2 + r2*a3 + r3*a4 + r4*a5 = s1

a1 + r2*a2 + r4*a3 + r1*a4 + r3*a5 = s2

a1 + r3*a2 + r1*a3 + r4*a4 + r2*a5 = s3

a1 + r4*a2 + r3*a3 + r2*a4 + r1*a5 = s4.

Then we can find the five roots by taking the inverse Fourier transform:

s0 + s1 + s2 + s3 + s4 = 5*a1

s0 + r4*s1 + r3*s2 + r2*s3 + r1*s4 = 5*a2

s0 + r3*s1 + r1*s2 + r4*s3 + r2*s4 = 5*a3

s0 + r2*s1 + r4*s2 + r1*s3 + r3*s4 = 5*a4

s0 + r1*s1 + r2*s2 + r3*s3 + r4*s4 = 5*a5

We already know that s0 = x1 + x10 + x2 + x9 + x4 + x7 + x8 + x3 + x5 + x6 = -1, by axiom 1, but s1, s2, s3, and s4 must be calculated via their fifth powers as sums of 5th roots of unity.

The algebra required to solve for s1^5 is so long-winded that it took 2 whole years since I started writing this post before I finally managed to concentrate on it long enough to solve it. There are 3125 values, of 70 different types, to sum in the expanded expression. Each term consists of a product of 5 values of the form a(n), multiplied by a 5th root of unity, each of which need to be expanded into a pair of x(n) values. Here is the result:

(a1 + r1*a2 + r2*a3 + r3*a4 + r4*a5)^5 = -196 - 130*r1 + 255*r2 - 20*r3 + 90*r4.

After substituting into this expression the respective values for r1, r2, r3, and r4 that we calculated way back in the first post, it becomes:

s1 = -979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5)

Amazing! I always get a feeling of wonder when I see such large and arbitrary-looking numbers in a formula for such an easy to define value. The only patterns I can see in these numbers are that -979, -275, -220, and 275 are all multiples of 11 - the degree of the roots we are calculating - and that -275, -220, and 275 are all multiples of 5 as well. The divisibility by 5 occurs because all the terms containing a value r(n) could have their a(n) values cyclically permuted to make 5 different terms having the same value, forcing the total number of r(n)-containing terms to be a multiple of 5 for each value of n.

The expressions for s2^5, s3^5, and s4^5 can be found by substituting out powers of r1 for the corresponding powers of r2, r3, and r4 respectively. Their values are:

s2^5 = -979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5)

s3^5 = -979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5)

s4^5 = -979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)

Now we need to take 5th roots of each of these expressions. The trouble here is in finding out which 5th root to use. As I said in my first post on roots of unity, I am defining c^(1/n) to be the value x having a polar angle equal to 1/n that of c, such that x^n = c, and therefore x has an angle between 0 and 2*pi/n radians. For the other nth roots of c, it needs to be multiplied by one of the nth roots of unity. But we don’t know what s1's polar angle is, so we don’t know if it’s 1, r1, r2, r3, or r4 times (s1^5)^(1/5).

I haven’t found any pattern in which 5th root to choose when, but a calculator can check that:

s1 = r1*(-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5)

s2 = r1*(-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5)

s3 = r4*(-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5)

s4 = r4*(-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5)

Now we can calculate our a(n) values:

a1 = (-1 + r1*(-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5) + r1*(-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5) + r4*(-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5) + r4*(-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5))/5

a2 = (-1 + (-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5) + r4*(-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5) + r1*(-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5) + (-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5))/5

a3 = (-1 + r4*(-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5) + r2*(-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5) + r3*(-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5) + r1*(-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5))/5

a4 = (-1 + r3*(-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5) + (-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5) + (-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5) + r2*(-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5))/5

a5 = (-1 + r2*(-979 - 275*√5 - 220i*√(10 - 2√5) + 275i*√(10 + 2√5))^(1/5) + r3*(-979 + 275*√5 - 220i*√(10 + 2√5) - 275i*√(10 - 2√5))^(1/5) + r2*(-979 + 275*√5 + 220i*√(10 + 2√5) + 275i*√(10 - 2√5))^(1/5) + r3*(-979 - 275*√5 + 220i*√(10 - 2√5) - 275i*√(10 + 2√5)^(1/5))/5

Unfortunately, since Unicode lacks a fifth root symbol (that I am aware of), I had to write the 5th root of x as x^(1/5).

Anyway, we now know the values of x1 + x10, x2 + x9, x3 + x8, x4 + x7, and x5 + x6.

Since x1 and x10 are complex conjugates, (x1 + x10)/2 is the real part of x1. This is the same value as cos(2*pi/11), and it is just a1/2.

Here is an image of what the expression for cos(2*pi/11) actually looks like when written out (with fifth-root symbols in place of x^(1/5)), just to show you how long it gets.

To figure out the value of, say, x1, we will be needing both x1 + x10 and x1 - x10. We already know the x1 + x10 = a1. Let’s call x1 - x10 = t1.

t1^2 = (x1 - x10)^2 = x2 + x9 - 2 = a2 - 2

So, t1 = √(a2 - 2). And just like a1 = 2*cos(2*pi/11), t1 = 2i*sin(2*pi/11).

So:

sin(2*pi/11) = √(2 - a2)/2 = √(55 - 5*(s1^5)^(1/5) - 5*r4*(s2^5)^(1/5) - 5*r1*(s3^5)^(1/5) - 5*(s4^5)^(1/5))/10.

If written out in full, this expression would look similar to the one given above except that:

the numerator is under a square-root sign

it starts with 55 instead of -1 and then subtracts the 5th roots instead of adding them

All of the 5th roots are multiplied by 5

The 1st and 4th ones don’t get multiplied by r(n) values.

The sines and cosines of 4*pi/11, 8*pi/11, 6*pi/11, and 10*pi/11 can be found by doing operations on a1, a2, a3, and a4 respectively.

--------------------------------------

Whew! That was way more complex than the formula for the 7th roots of unity. Next up is the 13th roots of unity, and I don’t think they will be nearly as hard.