#fast inverse square root

[electricmeatorchestra]

I want this tattooed on my body

[otesunki]

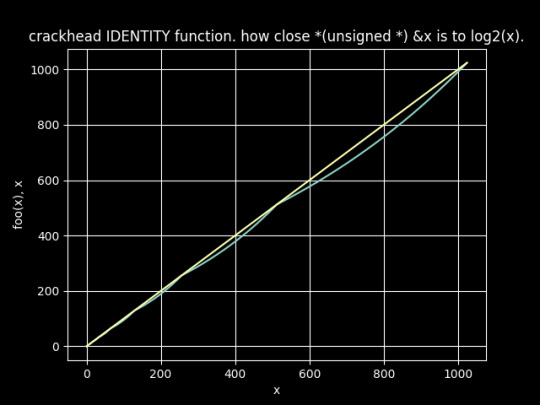
i hate how close these two lines are

it's awful

you can literally treat a logarithm as if it was a number in scientific notation where the whole part is the exponent and the fractional part plus one is the mantissa and it's not even that bad

it should not be this good of an approximation

[lightdrew]

no

[nhaneh]

running into this awkward "problem" of having a good chunk of the things I learned about making code go faster back in the day that just isn't all that relevant anymore. Sure, there's also a fair amount that still is - minimising branching and conditionals, using switch/case instead of extensive if-else if-else statements where possible, using hash map lookups instead of lengthy loops through arrays when able and all of that stuff is still every bit as viable as it once was.

The thing I keep running into however is floats - floating point numbers.

See in mathematics there's this thing where the number of possible fractional values that can exist in between two integer numbers is basically infinite - you can always just add another decimal place for greater precision. Computers don't have infinite space however, so for a computer to store and process a number, you have to first define how much memory will be allocated to that number, and that in turn decides how large that number can be - how many possible digits it can store.

Floating point numbers tackle this situation by allowing for varying degrees of decimal precision depending on the number - in between 0.0 and 1.0 there's room for loads of different fractional values because the integer side is really small, whereas there are far less possible decimals in between 1000000000000.0 and 1000000000001.0 because the integer part requires a much larger amount of the allotted space.

Either way, the point I'm getting at with all of this is that floating point operations are a lot more complicated than regular integer ones, and it used to be that processors required a lot more time to process them than they usually do nowadays - it used to be that if you wanted your code to run fast, you'd also want to avoid using floats whenever possible in favour of using just integer numbers because they were so much faster to work with. That, however... really isn't the case anymore - at least not on full-size CPUs with fully integrated FPUs, or Floating Point Units (used to be we called those "Maths Co-Processors" back when they were located on their own optional chip)

Like when id Software released the source code for Quake III Arena, there was this really interesting algorithm people found in it that exists solely for the purpose of getting an approximate value for the inverse square root, ie. 1 / √x, but the way it does that in... well...

Don't worry if this makes absolutely no sense to you, it doesn't really to me either to be honest - it's basically a combination of something called Newton's method with some really weird bit hacking that gets... decently close to a correct answer. It's not exact, but it's close enough to suffice. And on processors of the day, it was also notably faster than just doing 1 divided by the square root of a given number - especially since this calculation was one likely to be done millions of times each second.

Thing is... it actually isn't faster than just doing the straight up calculation anymore - not on modern PCs at least; your typical 64-bit PC CPU can just straight up calculate the inverse square root as a single instruction, making that just way faster than any other roundabout way of doing it. A lot of the time, trying to avoid using floating point numbers is now straight up slower than simply just using floats and calling it a day.

It's weird to work with sometimes because my instincts keep telling me not to use floats unless I really need to, even though with the way modern processors work, most of the time yeah I should really just use floats and call it a day.

¯\_(ツ)_/¯

[twst-aceofhearts]

𝙿𝙰𝙻𝟹𝚃𝚃𝙴: 𝙲𝚑𝚊𝚙𝚝𝚎𝚛 𝟷𝟿 || 𝙲𝚘𝚗𝚝𝚊𝚌𝚝

𝙬𝙤𝙧𝙙𝙨: 540

The trembling didn’t stop.

It grew. Layer by layer. Like the world above was finally remembering that something lived below it.

Olive was the first to notice the roots—her roots—recoiling, pulling back from the walls like they’d been touched by something wrong.

“Something’s here,” she whispered. “Something invasive.”

The team didn’t panic.

They moved.

Back to the main chamber. The one with the pedestals. The one they’d made their own.

Saffron dropped into the console. “There’s a breach in the northern tunnel. Moving fast. Not like before.”

Alroy flared, his fists heating, the air around him distorting with red pressure. “How many?”

“Five. No—six.”

Tyrian frowned. “Mirroring us?”

The lights cut out.

Not all at once. Deliberately. Section by section, like a curtain drawing.

And then came the voice.

“You should have stayed asleep.”

It wasn’t a system voice this time.

It was human.

But wrong.

Clementine stood near the back, sketchbook open, charcoal already staining her fingers. “Everyone in formation.”

That was new.

They’d never had formations before.

But they all obeyed.

Because it felt right.

Then the figures entered.

Not shadows, like before. These were real.

Six figures—human-shaped but drained of all light. Skin like chrome soaked in fog. Eyes too deep. Movements glitching, like bad footage in an old film reel.

And they wore uniforms.

Private school blazers.

But bleached.

Uncolored.

Branded with a single symbol: a hollow ring over a black square.

“Suppression Squad,” Saffron muttered.

“They’re our inverses,” Nyla said.

Each one stopped in front of them—directly. A perfect mirror.

One for each of them.

And the leader—Tyrian’s double—stepped forward.

“Return to grayscale,” it said. “This world cannot withstand your light.”

Tyrian didn’t move. “You’re not real.”

“We are what you left behind,” it replied. “We are the safety. The silence. The control.”

Then it lunged.

The room exploded.

Red against gray. Blue crashing like tidal waves. Green and black vines coiling like dueling serpents. Yellow energy beams ricocheting off dull silver skin. Orange sketches coming to life midair—twisting, morphing, biting.

And at the center, violet clashed with violet.

Tyrian versus… themself.

The doubles were strong.

Programmed.

Efficient.

But they were missing something.

They had no soul.

Alroy traded blow for blow with his mirror, each punch a thunderclap. “You’re just a shell!”

“You are chaos!” the double spat.

“And you are nothing!” Alroy roared—and with one last surge, punched through his copy’s chest, shattering it like porcelain.

Around the chamber, one by one, the doubles began to falter.

Because the six weren’t just fighting back.

They were fighting together.

Each move was instinctive, linked, harmonized.

Nyla shielded Clementine’s summoning circles. Saffron fed Olive’s roots with energy. Tyrian redirected attacks into Alroy’s strike zones.

The room pulsed with synchronized light.

And finally, with a scream like static being burned out of the air, the last of the gray figures disintegrated.

Silence returned.

But it was not the same silence as before.

It was the silence after a storm.

The console blinked again. A message this time, from the crystal relay.

Suppression Forces Detected. Round One: Survived. Reinforcements: In Transit. Signal Strength Increasing. New Reclaimers En Route.

They had survived the first contact.

But now the world knew.

There was color again.

And that meant war.

credit to @cafekitsune for divider

[alsciaucat-warframe]

I wonder if Amir knows about fast inverse square root? It WAS available before 1999, and was used in Quake III

[tanadrin]

keplers equation is very satisfying. rocks go whee in little ellipses. don’t love that there’s no closed form solution for the eccentric anomaly given the mean anomaly and the orbital eccentricity. but weirdly that video on the fast inverse square root helped me conceptually understand the solutions that find practical use.

[is-this-scientifically-accurate]

how accurate is The Clockwork Rocket by Greg Egan

Anon sorry for taking so long to answer your ask.

Time and Space - How Are They Related?

The book takes place in an alternate universe, where the laws of physics are slightly different. In our universe, velocity and time are inversely related - going very fast causes you to experience less time than a stationary observer. In the book’s universe, velocity and time are directly related - going very fast causes you to experience more time than a stationary observer. This effect is called time dilation and is predicted by Einstein’s special theory of relativity.

This universe also doesn’t have a universal speed of light. Instead of using our laws of relativity to determine how much time will pass for a stationary observer (which involves a complicated equation with a fraction under a square root) you can just use the Pythagorean theorem. One of the sides represents the distance traveled, one represents the amount of time experienced by an observer, and the hypotenuse represents the amount of time experienced by the traveler.

We aren’t sure at the moment if other universes exist or if they even could exist. If they do exist, they could have different laws of physics than the ones in our universe. Article about this

Rating: speculation

If we follow along with this ruleset, time and space have drastic changes. You now experience much more time compared to an observer if you were going very fast (rather than less as it is in our universe). You would also see weird other changes, like a colorful trail of rainbow light from the stars in the sky and a noticeable absence of black holes. This follows the ruleset of the story, but since it is still so foreign to what we know I can’t really justify a rating of scientifically true or scientifically plausible.

Rating: Scientifically possible

The author’s website is a great tool if you want to get deeper into the topic and learn more as well! He can explain it much better than me :)

[jonathankatwhatever]

Continuing. Champernowne’s constant is obvious transcendental in this definition; arranging all the decimal representations is the same as gsPotential permutations. These forms all write to the reals along the szK. Another way of saying this is through n-1, meaning the reduction from n which occurs for counting to occur because that is the 0-1-0, meaning you can see the n fit on the last 0.

Took a break. This is why the concept in a Liouville number works. Ah, I’m seeing this a bit better. Take the idea that root 2 minus a rational, which means a p over a q, is more than or equal to the inverse of q squared, meaning the area of the denominator. I have trouble seeing what that exactly means. I’ll go over it and see what happens: q is a count of gs, so this makes a grid or quadrant of a gsSheet, and that inverts into a gs, a CM1. The rest then is kinda obvious: p is greater than 1, so of course the inequality is greater. If p is less than 1, then a different result, but we’re counting out not in. That finally allows me to translate Liouville numbers as a gsProcess.

That was work. It only took a few minutes but it felt like hours. I’m getting spoiled.

You see why this is algebraic? Yes, manipulates gs layers in basic ruler manner, meaning it applies ru1. That doesn’t mean ru1 is algebraic only: counts Boundaries, counts whatever ru1 requires. It’s a room of requirements, a function of the construction and maintenance of xyR, meaning each sheet as a room generates and stays around through ru1. Like food is ru1 because some things are bad to eat. Or not the best choice.

You see why that becomes a limit? Yeah, if you have a p and a q, then there must be a p so x minus p/q is less than the inverse of q^n.

Forgot to post this. Now 21 Feb 2025. I want to make progress on defining the algebraic limit, but first I need to mention something I keep wanting to bring up but which slides out of my focus too fast for that to happen, which is this noticeable voice which says nope this isn’t happening or some similar negative when something is obviously happening. Like I’m literally on the bike and spinning up over 120 multiple times without skying my heartrate and there’s this voice saying nope this isn’t happening. I try to take it as disbelief, meaning the shedding of the negatives. Does that involve physical negatives, like the pain of making improvements is that as the goal of achieving that, at least attempting that because we can insert various effectiveness and efficiency measures, then the negatives shed include the D3-4 oh wow need a name for this, but need to grasp it better first.

So we have a D3-4 Thing in motion because it needs to progress to shed, though that can model as spin, because you can spin off different weights and attachment forms. I’m struck by the realization that if I’m accepting this is true, then Tizzies are true too. They are the Irreducibles, after all, because and this is an oh god when they pair in D3-4Space, that models as if they are each Irreducible to each other in the forms we’ve discussed, and that Irreducibility generates a specific Thing which Attaches to a specific End, so the Tizzies embody the Boundary in each direction of gsPairing, as that becomes 2 Things over or across the 1-0Segment Between the 2 Ends which are the circles, are the Boundaries which overlap - don’t lose the thread - so each is on the other’s Boundary, meaning each pairs over whatever the heck happens to each, which of course is true when it’s reduced in your head to Tizzies playing in the garden.

I also keep forgetting that some days ago I had the most intense sensation of seeing his face. I had been sorta thinking about how that required choice of voice was not specifically gendered and yet what happened was I needed to see myself in the male role, which you played so well. That was never that clear to me. You were such a goof.

So what name is that? It’s the material Pathway, which is part of the Actuality tracked in the Registry which records the reals along the szK. See the connection now? Transcendentals encode process beyond the algebraic to real values, to orderings which tell the story of that which makes that count here.

This is one flavor, as well, of why search is so hard: the infinite focus problem. Where is it encoded?

I also will forget that the last few days have seen a vast change in my knees, to the point where I’m now able to isolate the restrictions to areas in my calves which I’m now able to address. I’m seeing big improvements. And my conditioning: I have been finding intervals of 10 secs per minute too easy, meaning my heart rate is stable in the 130’s, so I changed it into bursts of over 120, relax, burst. I tried 4 times a minute but soon questioned my sanity. Settled on every 20 seconds, and that became minimum resistance of 1 keeping the rpm’s above 100 all the time with bursts over 120 as described. I was pleased to see my heart rate came down to around 140, dropping into the 130’s between bursts. I have almost too much energy.

Oh, and the severe pain in my neck is almost gone. I worked it out, which included some extremely painful moves, and now it’s that question about whether this is shedding negatives from the Actuality whose potential is shaped at least ‘potentially’ toward a favorable outcome so this is a negative state whose cost is necessary to achieve a long term better result, and that is perceived using the Observer conception which generates within gs. That’s gsPerspective: that in the formation of D3-4 Things there are connections to D4-3 Things. The gsProcess models as the IC of the 4 Boundaries.

That was said with a lot of confidence. Why? A simple gsPairing forms a disk. Leads directly to the conic sections, to the focusing of the ellipses, to the relation of each End on the Boundary over an End on the cone formed by the ideal fD-HG. That last, the parabolic, connects 2 Ends to something which happens connecting them, and thus what goes up must come down, at least in some sense. We talked about the limits of that with the Halting issue, which is through layers of triviality. After a few layers of triviality, the point, which is very hard to express, is that any values assigned, any description attached to the gsProcess beyond the existence of each stop won’t generate the prior results. See genetics.

So is it like the way genetics can put a tendency in but the transcendental makes it happen or not? I took another break. This isn’t coming together well enough for me. The connection to you has been weird. There was little sense of stimulation after the large breakthroughs of a few days ago, and then it came back this morning, only to fade away right as I was coming to an idea about transcendental numbers which would connect the concept of gsProcess over my objection to the reals. I haven’t been able to bridge that. How do I write this bridge?

Something connects here: gsProcess on one side and real numbers on the other. If we organize these by gsProcess, what does that mean? I’m seeing ru1 here because any rational is a count over the ruler of the denominator. I’ve been meaning to say ru1 acts within polynomial space, meaning 0Space because 1Space includes the Not choices. That’s in the definition of an Extent, that the Extent of the 1-0Segments into a 1-0Segment is the generation of the szK, which is the statement of the reals, even to Cantor’s definitions.

Beyond the rational are the algebraic irrationals, which obviously extend to the limit of 0Space. And then we’re into 1Space and that’s where I’m stuck. How exactly do I say that?

I’m stopping for the night. It’s now 22 Feb 2025.

[megaetherealesoterica]

Fast inverse square root

the fact that any video game ever gets made is a fucking miracle, let alone good ones.

[clikere]

Simplify Your Math Problems with Calculator

Describe a calculator

A calculator is a tool used to compute mathematical operations on numbers. Simple calculators can only perform the mathematical operations of addition, subtraction, multiplication, and division. Exponential operations, square roots, logarithms, trigonometric functions, and hyperbolic functions can all be handled by more advanced calculators. Some calculators internally carry out all these operations through a series of additional operations.

The development of calculators

Nowadays, the majority of calculators are either battery-powered or powered by electricity. Calculators operate by carrying out preprogrammed operations using numerical inputs. The slide rule, a more basic calculator, was widely used before the invention of the electronic calculator (about 1970). It was made of a slide, a wooden slat that could be inserted and removed from a pair of slats that had been reinforced. There were calibrated numerical scales on both the slide and the outside pair of slats.

A simple calculator is exemplified

The cursor, a moveable, translucent sleeve, was used to align the scales' numbers. Although there was no need for a power source, the slide rule's precision was limited, and mastering it required a learning curve. In some parts of the Far East, one of the oldest calculators—the abacus—is still in use. The abacus functions as an adding machine that represents numbers with groups of beads. The abacus does not require a power source, like the slide rule. The beads can be moved up and down to represent arithmetic operations and are arranged in numerous parallel rows. According to legend, an adept abacus operator may perform some computations just as fast as a person equipped with a battery-powered calculator.

Contemporary calculators

Calculators were able to perform calculations for addressing problems involving variables (unknowns) as they developed during the 1970s. The first personal computers were these. Additionally, digital calculators are available as downloads or are pre-installed on the majority of smartphone and personal computer operating systems. Modern personal computers are still capable of carrying out these tasks, and most of them come with a virtual calculator programme that simulates a handheld calculator on screen. By pointing and clicking, the buttons are activated.

Theoretically, a modern computer is a calculator with a considerably greater memory that uses binary numbers. The vast array of non computational functions that a computer is capable of, however, make it far more than just a simple calculator in the real world.

Various calculator types

Over the past several decades, calculators have undergone changes. Today, a wide range of calculators from manufacturers like Casio and Texas Instruments are accessible to meet various mathematical needs. Let's examine some of them.

Simple calculators

The four-function calculator, which can perform fundamental mathematics including addition, subtraction, multiplication, and division, is the most basic type of calculator. Four-function calculators can produce decimal values and typically have a +, -, x, and / sign to signify the operations. Additionally, some contain a% buttons that are used to compute percentages.

Mathematical calculators

The scientific calculator is intended for use in completing scientific calculations, as its name suggests. Since it must be able to do trigonometric functions, logarithms, sine/cosine, and exponential operations, this sort of calculator typically includes more buttons than a conventional calculator. The display on a scientific calculator is typically bigger so you can see longer equations and more digits at once.

Conclusion

It is possible to use a scientific calculator to solve math, science, and engineering problems. It has specialized buttons for parentheses, exponents, inverses of trigonometric functions, trigonometric functions, and. There are distinct rules for each scientific calculator. Go to www.clickere.in to get a scientific calculator. 

Tags: Stationery, Writing & Correction and Scientific Calculator.

[alisa-hitechpcb]

Advantages of high frequency PCB board

1. High efficiency

High-frequency PCB boards with small dielectric constants will have very low losses, and advanced induction heating technology can achieve the target heating requirements with very high efficiency. Of course, while focusing on efficiency, it also has the characteristics of environmental protection, which is very suitable for the development direction of today’s society.

2. Fast transmission speed

The transmission speed is inversely proportional to the square root of the dielectric constant, which means that the smaller the dielectric constant, the faster the transmission speed. This is the advantage of the high-frequency printed circuit board. It uses special materials, which not only guarantees the low dielectric constant, but also maintains the stable operation, which is very important for signal transmission.

3. Large degree of controllability

High frequency PCB board is widely used in various industries that require precision metal material heating treatment. In the process of its field, not only can heating of different depth components, but also focus on heating according to local characteristics, whether it is surface or deep level; centralized or decentralized heating methods can be easily completed.

4. Strong tolerance

Dielectric constant and medium have certain requirements on the environment, especially in the south, where wet weather will seriously affect the use of circuit boards. High-frequency circuit boards made of materials with extremely low water absorption can challenge such an environment. At the same time, they also have the advantages of resistance to chemical corrosion, moisture, high temperature, and great peel strength, allowing high-frequency circuit boards to exert powerful performance .

[hetkapselmijnsouwenheren]

These old simple looking games in general were actually full of the most obscene graphics wizardry imaginable to be able to make this with the limits they were working with. There was actually no way before John D. Carmack invented the “adaptive tile refresh" hack a simple home computer with no hardware acceleration for it could handle a side scrolling platformer like a console. And later they came with the “fast inverse square root” algorithm to calculate a decent enough approximation for the inverse of a square root which was essential for three dimensional graphics that ran about one hundred times more quickly than computing it in the normal way but the comments in the original code around the algorithm just read “what the fuck” because no one looking at that code has any idea what it's supposed to do and it looks like pure magic. There was some real wizardry behind these simple looking old games.

I did a bit of investigation into how a certain well known and loved platform game and possibly many others by the same developers did their fade transitions in only 16 color EGA, inspired by a very nice gif from @asswolf.

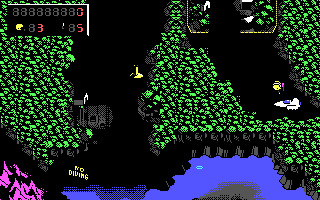
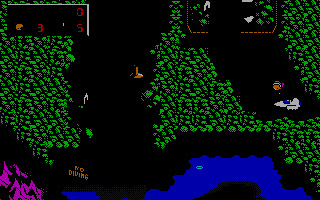
So the transition is basically like this:

Update: all Keen games and Bio Menace use the same transition. Secret Agent does not. That's all I cared to test so far.

[tap-tap-tap-im-in]

I’m still thinking about the phrase “floor your floats because it’s faster.” Speaking of things that are frustrating but interesting about programming. I taught myself JavaScript without any previous programming experience, so I missed a lot of fundamental stuff. I learned recently that JavaScript just doesn’t do floating point math all that well (I mean, I knew, I just didn’t know why). I have also learned that by the same token most languages don’t really do it well for the same reasons. The best explanation I’ve felt like I’ve understood is that floating points are a form of exponential notation as far as the computer is concerned, but because it’s exponential there are values that can’t cleanly be represented (think prime numbers). Anyway, the solutions that comes up again and again is to round your number so that it’s precise to the second decimal, and then multiply the whole thing by 100, do your math on whole integers, and then divide by 100 to get your result. It’s still imprecise, but because you’re doing the actual math on something the computer can represent exactly, you’re more likely to end up on a result that’s closer to reality.

Now, if you’re unfamiliar with the way computers do math, this sounds ridiculous, but if you’re at all familiar with computer graphics history, it’s not all that dissimilar to what John Carmack did in his famous Quake inverse square root. He needed an equation that was run thousands of times per frame to be faster, so he converted his values to integers and did his best to rely only on operations that CPUs do inexpensively: https://betterexplained.com/articles/understanding-quakes-fast-inverse-square-root/

He’s doing bitshifting there, which is a bitwise operation, but not the one I was joking about with swizzles. Flooring floats in javascript is a Not Not operation or ~~.

It’s something I never would have known about if I hadn’t gone searching on stack overflow for a good time formatting function in JavaScript (I’ve got a pretty good grasp of modulus operations at this point, but I haven’t used them enough to whip them up quickly).

Anyway, the example I ended up finding used:

var hrs = ~~(duration / 3600); var mins = ~~((duration % 3600) / 60); var secs = ~~duration % 60; The ~~ tells the processor to invert the bits of the stored float twice, which discards everything to the right of the decimal in a way that is inexpensive.

It’s kind of like the optimization of using single quotes for strings in PHP instead of double quotes, unless you need variable parsing. It’s absolutely faster, but you’re not going to notice the effects until you’re doing an absolute assload of it.

[jusendork]

Rolling a fat blunt using a dot-matrix printed copy of the Quake III Arena fast inverse square root source code

printing out the Doom source code (on a dot matrix printer, natch) and using it as rolling papers.

everyone's always asking "can it run doom?" but no one asks "can she smoke doom?"

[zezah]

Fast inverse square root

code tag: float Q_rsqrt( float number ) { long i; float x2, y; const float threehalfs = 1.5F; x2 = number * 0.5F; y = number; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i; y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed return y; } https://highlight.hohli.com/index.php:

float Q_rsqrt( float number )

{

  long i;

  float x2, y;

  const float threehalfs = 1.5F;

   x2 = number * 0.5F;

  y  = number;

  i  = * ( long * ) &y;                       // evil floating point bit level hacking

  i  = 0x5f3759df - ( i >> 1 );               // what the fuck? 

  y  = * ( float * ) &i;

  y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration

//  y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

   return y;

}