#matric part 1 math

[rosesrded]

09.04.2025 (wed)

Day (1/30) COLLAB CHALLENGE

3:38 hrs on ypt ;) + (~ 20 mins)

💤 Sleep ~ 4hrs + 2:30hr nap 💤

Today was BRUTAL y'all. Had double phy, chem, bio AND math. It wasn't like phy chem bio math phy— nah AH. It was BIO BIO CHEM CHEM MATH MATH ugh. By math I started to forget who I was. And these tr be giving barely any breaks 😭

Couldn’t revise the notes I made yesterday, so just went over Lec 1, but my focus was trash (less than 10 hrs sleep over the past days which is wild considering I was averaging 10 hrs/day during break). Decided to nap because I was absolutely useless by then. Planned for 1 hr, woke up after 2.5 hrs and turns out that’s my perfect nap length. I just auto-wake at that point.

Post-nap:

Dinner

Math hw

Watched a one-shot on Matrices for the test

Did extra questions tr gave us

Went through my notes + reader

Skimmed through Determinants reader part (till ex: 4.2)

Gt rev notes of determinants in the morning

Also,

Read till ideal & non ideal solutions in chem in the morning. I was planning on reading haloalkanes and halo arenes but my dum ass took chem part 1 instead of 2 so compromised.

Wanted to squeeze in a Chem lec, but I gotta sleep fr—can’t make naps a lifestyle. I ain't got time for that 😭

Until next time ~

(⁠ ⁠˘⁠ ⁠³⁠˘⁠)💗

[shankhachil]

Countdown to JEE (Main): Week 1/33

Yep, I'm doing it. Forgive my attempt at aesthetics (but if you like it, then don't).

I've been a bit less productive than usual this week, mostly because I've been spending far too much time on Discord — should really cut down on that — and also staying up late, which has a terrible impact on my daily activity level.

But, well, it's going.

Targets: 3 topics of each subject covered per week; 400 questions solved per week, at least 80 of each subject

Topics covered:

Physics: Potential and Capacitance; Motion in One and Two Dimensions (2/3)

Chemistry: Halogen Derivatives; Alcohols, Phenols, and Ethers; Chemical Thermodynamics and Thermochemistry (3/3)

Mathematics: Definite Integrals; Area Under a Curve; Matrices (3/3)

Looks like I'll need to work on Physics, then. I'm a bit behind with respect to Allen, but my physics tuition is helping me along in that regard so no need to worry.

Questions solved:

Physics: - Allen Electrostatics module, JEE (Main) archives — 34 questions, 30 correct - Tuition Potential and Capacitance module — 192 questions, 172 correct - Tuition Vectors and Motion in Two Dimensions module — 108 questions, 102 correct Total: 334/80 questions, 304 correct

Chemistry: - Allen Thermodynamics (Part 2) module, O1, O2 and JEE (Main) archives — 82 questions, 76 correct - Himanshu Pandey, Alcohols, Phenols, and Ethers chapter — 110 questions, 93 correct Total: 192/80 questions, 169 correct

Mathematics: - Allen Definite Integrals module, O1, O2, O3 and O4 — 75 questions, 61 correct - Allen Area Under a Curve module, O1 — 30 questions, 23 correct Total: 105/80 questions, 84 correct

GRAND TOTAL: 631/400 questions, 557 correct

I've been having some trouble with calculus, as you can see. I'll need to work on that as we go. Nothing to do but practise.

Upcoming tests:

07/05/24 (Friday) — test at physics tuition center. Topics: Motion in One and Two Dimensions; Units and Dimensions; Potential and Capacitance; Chemical Thermodynamics and Thermochemistry; Alcohols, Phenols, and Ethers.

09/05/24 (Sunday) — Aryabhatta National Maths Competition

That's all for this week.

[admiral-crow-is-watching]

What part of maths letters commonly inhabit (Part I, Latin)

a,b,c: Some kind on constants. Could be anything.

A, B: probably set theory.

B: Could be open balls, could be a binomial distribution.

C: constants of integration in a normal font, complex numbers in blackboard font.

d, k, p, q: Dimensions of something or other

D: Could be another constant of integration, or possibly a domain of discourse if it looks fancy.

E: Expectation! You're doing probability.

e: Euler's number. Will not stop turning up absolutely everywhere.

e, g, h: Group theory or other algebra. You are unlikely to also see numbers.

f, F, g, G, h, H: The classic choice for functions.

H: Whatever this is is named after Hamilton.

i: square root of -1, complex numbers, right up there with e in turning up everywhere.

I: Indicator function, identity matrix, information. An underratedly versatile letter.

i,j,k: Another classic triple act. Could be either index variables or something three-dimensional, like unit vectors or quarternions.

K, M: upper bounds on some kind of modulus. Look for || everywhere.

L, l: Most likely likelihood functions from statistics.

m,n: Integers! Index variables, sequences, induction, these two have you covered.

M: Matrices, welcome to linear algebra.

N: Natural numbers in a fancy font, a normal distribution in a normal one.

O: either big O notation and you're doing computer science; or if it's blackboard font, you're doing octonions and may your gods go with you.

p, P, q: Probability theory, again.

P, Q: formal logic. Usually seen in conjunction with lots of arrows.

Q: Rational numbers, usually blackboard font, you are most likely in algebra.

R: Real numbers, you are in analysis.

r: Something has a radius. It could well be a very abstract multidimensional radius.

s: Possibly generating functions, especially in conjunction with F and G. Not one of the more common maths letters.

t, T: Something is happening over time.

v: Vectors are happening.

u, U: whatever this is, you're too deep.

w: Something in four variables is happening.

x,y,z: the classic variable set. unknowns, vectors, scalars, there's nothing this gang of three can't do.

Z: Integers in blackboard font; a standard normal distribution in a regular one.

[korshubudemycoursesblog]

Unlock Your Future: Learn Data Science Using Python A-Z for ML

Are you ready to take a deep dive into one of the most in-demand skills of the decade? Whether you're looking to switch careers, boost your resume, or just want to understand how machine learning shapes the world, learning Data Science using Python A-Z for ML is one of the smartest moves you can make today.

With Python becoming the universal language of data, combining it with data science and machine learning gives you a major edge. But here’s the best part—you don’t need to be a math genius or have a computer science degree to get started. Thanks to online learning platforms, anyone can break into the field with the right course and guidance.

If you’re ready to explore the world of predictive analytics, AI, and machine learning through Python, check out this powerful Data Science using Python A-Z for ML course that’s crafted to take you from beginner to expert.

Let’s break down what makes this learning journey so valuable—and how it can change your future.

Why Data Science with Python Is a Game-Changer

Python is known for its simplicity, readability, and versatility. That's why it’s the preferred language of many data scientists and machine learning engineers. It offers powerful libraries like:

Pandas for data manipulation

NumPy for numerical computing

Matplotlib and Seaborn for data visualization

Scikit-learn for machine learning

TensorFlow and Keras for deep learning

When you combine these tools with real-world applications, the possibilities become endless—from building recommendation engines to predicting customer churn, from detecting fraud to automating data analysis.

The key is learning the skills in the right order with hands-on practice. That’s where a well-structured course can help you move from confusion to clarity.

What You’ll Learn in This A-Z Course on Data Science with Python

The course isn’t just a theory dump—it’s an actionable, practical, hands-on bootcamp. It covers:

1. Python Programming Basics

Even if you’ve never written a line of code, you’ll be walked through Python syntax, data types, loops, functions, and more. It’s like learning a new language with a supportive tutor guiding you.

2. Data Cleaning and Preprocessing

Raw data is messy. You’ll learn how to clean, transform, and prepare datasets using Pandas, making them ready for analysis or training machine learning models.

3. Data Visualization

A picture is worth a thousand rows. Learn how to use Matplotlib and Seaborn to create powerful charts, graphs, and plots that reveal patterns in your data.

4. Exploratory Data Analysis (EDA)

Before jumping to models, EDA helps you understand your dataset. You’ll learn how to identify trends, outliers, and relationships between features.

5. Statistics for Data Science

Understand probability, distributions, hypothesis testing, and correlation. These concepts are the foundation of many ML algorithms.

6. Machine Learning Algorithms

You’ll cover essential algorithms like:

Linear Regression

Logistic Regression

Decision Trees

Random Forests

Support Vector Machines

k-Nearest Neighbors

Naïve Bayes

Clustering (K-Means)

All with practical projects!

7. Model Evaluation

Accuracy isn’t everything. You’ll explore precision, recall, F1-score, confusion matrices, and cross-validation to truly assess your models.

8. Real-World Projects

Theory only goes so far. You’ll build actual projects that simulate what data scientists do in the real world—from data collection to deploying predictions.

Who Is This Course Perfect For?

You don’t need a Ph.D. to start learning. This course is designed for:

Beginners with zero coding or data science background

Students looking to enhance their resume

Professionals switching careers to tech

Entrepreneurs wanting to use data for smarter decisions

Marketers & Analysts who want to work with predictive analytics

Whether you're 18 or 48, this course makes learning Data Science using Python A-Z for ML accessible and exciting.

What Makes This Course Stand Out?

Let’s be real: there are hundreds of data science courses online. So what makes this one different?

✅ Structured Learning Path

Everything is organized from A to Z. You don’t jump into machine learning without learning data types first.

✅ Hands-On Projects

You’ll work on mini-projects throughout the course, so you never lose the connection between theory and practice.

✅ Friendly Teaching Style

No dry lectures or overwhelming jargon. The instructor talks to you like a friend—not a robot.

✅ Lifetime Access

Once you enroll, it’s yours forever. Come back to lessons any time you need a refresher.

✅ Real-World Applications

You’ll build models you can actually talk about in job interviews—or even show on your portfolio.

Want to start now? Here’s your shortcut to mastering the field: 👉 Data Science using Python A-Z for ML

Why Data Science Skills Matter in 2025 and Beyond

Companies today are drowning in data—and they’re willing to pay handsomely for people who can make sense of it.

In 2025 and beyond, businesses will use AI to:

Automate decisions

Understand customer behavior

Forecast market trends

Detect fraud

Personalize services

To do any of this, they need data scientists who can write Python code, manipulate data, and train predictive models.

That could be you.

From Learner to Data Scientist: Your Roadmap

Here’s how your transformation might look after taking the course:

Month 1: You understand Python and basic data structures Month 2: You clean and explore datasets with Pandas and Seaborn Month 3: You build your first ML model Month 4: You complete a full project—ready for your resume Month 5: You start applying for internships, freelance gigs, or even full-time roles!

It’s not a pipe dream. It’s real, and it’s happening to people every day. All you need is to take the first step.

Your Investment? Just a Few Hours a Week

You don’t need to quit your job or study 12 hours a day. With just 4–5 hours a week, you can master the foundations within a few months.

And remember: this isn’t just a skill. It’s an asset. The return on your time is massive—financially and intellectually.

Final Thoughts: The Future Belongs to the Data-Literate

If you've been waiting for a sign to jump into data science, this is it.

The tools are beginner-friendly. The job market is exploding. And this course gives you everything you need to start building your skills today.

Don’t let hesitation hold you back.

Start your journey with Data Science using Python A-Z for ML, and see how far you can go.

[renatoferreiradasilva]

Uma Estrutura Modular-Espectral para a Hipótese de Riemann: Uma Proposta de Operador com Simplicidade Imposta por Subespaços

Resumo

Este artigo propõe um problema teórico rigoroso inspirado na Hipótese de Hilbert–Pólya, com objetivo de modelar os zeros não triviais da função zeta de Riemann como autovalores de um operador autoadjunto definido em um espaço de Hilbert. A proposta central é a construção de um operador diferencial de ordem arbitrária com estrutura espectral modular, tal que cada subespaço modular contenha exatamente um autovalor crítico. A simplicidade espectral é imposta via restrições ortogonais e penalidades combinatórias. O artigo explora as implicações matemáticas, computacionais e heurísticas dessa abordagem, integrando análise funcional, teoria espectral, estatística de matrizes aleatórias e modelagem numérica.

1. Introdução

A Hipótese de Riemann (RH) afirma que todos os zeros não triviais da função zeta de Riemann possuem parte real igual a 1/2. A conjectura de Hilbert–Pólya sugere que esses zeros podem ser entendidos como espectro de um operador autoadjunto. Numerosos avanços computacionais (Odlyzko, 1987; 2000) demonstraram que os espaçamentos entre zeros se alinham com as estatísticas do Gaussian Unitary Ensemble (GUE), reforçando a interpretação espectral.

Neste trabalho, propomos uma abordagem modular: dividir o espaço funcional em subespaços Hj, cada um associado a um "modo" ou coluna de um ábaco espectral abstrato. Impomos, então, a restrição de um e apenas um autovalor crítico por subespaço Hj, correspondendo à unicidade dos zeros da zeta.

2. Formulação do Problema

2.1 Espaço de Hilbert e Operador Diferencial

Considere H=L2(R,w(x)dx), com peso w(x)∈C∞(R), e um operador linear diferencial formal: L=∑k=02nak(x)dkdxk, com coeficientes ak(x)∈C∞, definido em um domínio denso D⊂H, tal que: ⟨Lf,g⟩=⟨f,Lg⟩,∀f,g∈D.

2.2 Decomposição Modular do Espaço

Admite-se uma decomposição ortogonal: H=⨁j=1∞Hj, com base ortonormal {ϕj,k} tal que: Lϕj,k=λj,kϕj,k.

2.3 Condição de Simplicidade Modular

Postulamos que: ∀j,∃! k tal que ℜ(λj,k)=1/2, ℑ(λj,k)∈R,  e mult(λj,k)=1. Este conjunto {λj,kj} forma o espectro crítico do operador, análogo aos zeros não triviais da zeta.

3. Objetivos Teóricos e Operacionais

Demonstrar que L admite extensão autoadjunta L‾ com espectro discreto.

Estabelecer que {λj,kj}⊂σ(L‾) obedece: λj,kj=1/2+iγj,γj∼2πjlog⁡j, quando j→∞.

Provar que a inclusão de mais de um λ crítico por Hj viola a autoadjunticidade ou perturba a estatística GUE.

4. Penalidade Combinatória e Função de Custo

Defina a função penalizante: P=∑j=1∞(∑k1ℜ(λj,k)=1/2−1)2.

Temos que: P=0  ⟺  existe exatamente um zero crıˊtico por subespac¸o modular.

Essa função pode ser usada em modelos computacionais (ex: PINNs) para regularizar a busca por operadores consistentes com a RH.

5. Implicações e Perspectivas

A abordagem proposta fornece:

Um critério construtivo para operadores candidatos à Hilbert–Pólya;

Uma ponte entre estruturas modulares (como ábacos) e análise espectral;

Um método rigoroso para impor simplicidade espectral e alinhamento com os zeros da zeta.

Futuros desenvolvimentos incluem:

Construção de operadores discretos esparsos M∈C∞×∞ com uma entrada por linha/coluna,

Estudo da relação entre L e Laplacianos hiperbólicos,

Implementação computacional do modelo com redes neurais espectrais condicionadas por penalidades modulares.

Referências

Odlyzko, A. M. "The 10^{20}-th zero of the Riemann zeta function and 70 million of its neighbors", 1987.

Berry, M. V., Keating, J. P. "The Riemann zeros and eigenvalue asymptotics", SIAM Rev., 2000.

Mehta, M. L. Random Matrices, 3rd ed., Elsevier, 2004.

Titchmarsh, E. C. The Theory of the Riemann Zeta Function, Oxford, 1986.

Connes, A. "Trace formula in noncommutative geometry and the zeros of the Riemann zeta function", Selecta Math., 1999.

[shoshanews]

1. Learner Administration: IT Listing Reference: 8394Listing Status: Active Position Summary Company: SasolIndustry: Chemicals and EnergyJob Category: IT Learnership / Administrative SupportLocation: Sandton, Secunda, Sasolburg, and Durban, South AfricaContract Type: Fixed Term (12-month Learnership)Remuneration: Market-related stipendEE position: Yes – preference given to people with disabilitiesClosing Date: 17 April 2025 Introduction If you're a recent graduate or a motivated individual with a passion for IT, business operations, or data analytics, Sasol's Learner Administration: IT Learnership Programme presents an exceptional opportunity to launch your professional career. With over 70 years of global experience in the integrated chemicals and energy sector, Sasol is more than just a company — it's a purpose-driven organization committed to innovation, sustainability, and developing talent in South Africa. This 12-month structured programme provides a solid foundation for future career success in the tech and administration sectors, offering a blend of theoretical learning and practical workplace experience. With the demand for digital and analytical skills on the rise, this learnership is tailored for ambitious individuals ready to take the next step in their personal and professional growth. The programme is hosted across major Sasol locations including Sandton, Secunda, Sasolburg, and Durban, giving learners exposure to dynamic environments while equipping them with real-world industry experience. Importantly, this opportunity is part of Sasol’s inclusive development strategy, giving preference to individuals living with disabilities and promoting equal employment opportunities across the board. Job Description: The Sasol Learner Administration: IT Learnership programme is designed for candidates who want to develop both soft and technical skills within an administrative and IT-driven environment. The programme combines classroom-based theoretical training with hands-on practical learning, enhancing the employability of young professionals while preparing them for future roles in administration, technology, and analytics. Programme Overview: - Duration: 12 months (fixed-term contract) - Location: Sandton, Secunda, Sasolburg, Durban - Qualification: Matric/Grade 12 (minimum), Diploma or Degree advantageous - Areas of Exposure: Industrial Engineering, Software Engineering, Information Technology, Data Science, Full Stack Engineering, Cyber Security, Data Analytics - Target Candidates: Entry-level applicants with 0–1 years of work experience Theoretical Learning Modules Include: - Entrepreneurship - Business Operations - Customer Service - Business Accounting - Communication Skills - Computer Skills - Maths Literacy Practical Learning:Participants will work within Sasol’s Group Rewards & Human Capital Solutions division (OME: HCA), supporting various administrative and IT-related functions. Tasks include improving workflow processes, managing documentation, supporting performance monitoring, and learning how large-scale business systems operate in a corporate setting. Ideal Candidate: Sasol is searching for enthusiastic learners who demonstrate initiative, adaptability, and a commitment to personal development. The ideal candidate must have a genuine interest in IT and business systems and be willing to embrace a fast-paced, dynamic learning environment. Minimum Requirements: - Completed Matric / Grade 12 - Diploma or Degree (completed or in-progress) in one of the following disciplines will be an advantage: - Information Technology - Data Science - Software Engineering - Cyber Security - Computer Science - Industrial Engineering - Full Stack Engineering - Data Analytics - 0–1 year of relevant experience - Basic knowledge of Microsoft Office and PowerBI tools - Ability to work independently and in a team - Good verbal and written communication skills Preference: - Applicants with disabilities are strongly encouraged to apply - South African citizens only Role Responsibility: As part of the Learnership programme, learners will be tasked with contributing to the daily operations and ongoing administrative support of their assigned departments. Learners are expected to adopt a proactive approach to problem-solving and be actively engaged in both learning and practical assignments. Key Responsibilities: - Participate in all scheduled learnership training sessions - Assist in the development and management of administrative tasks - Utilize PowerBI and other data tools to support analytics initiatives - Ensure timely and accurate documentation of tasks and reports - Help improve workflow management processes - Provide exceptional customer service and support to internal stakeholders - Understand and comply with Sasol’s workplace safety and operational procedures - Develop project-based skills related to IT systems and business operations Skills & Attributes: Behavioural Competencies (BC): - Nimble Learning: Ability to absorb information quickly and adapt to change - Manages Complexity: Able to handle multiple tasks efficiently and with clarity - Self-Development: Actively seeks feedback and self-improvement - Demonstrates Self-Awareness: Understands own strengths and limitations - Ensures Accountability: Takes responsibility for tasks and outcomes Technical Competencies (TC): - Workflow Management: Manages time and tasks effectively - Action Planning: Plans and executes activities with precision - Policies and Procedures: Understands and adheres to company regulations - Performance Improvement: Identifies and acts on areas for performance gains - Execute and Coordinate Work: Follows through on assignments effectively Bonus Skills: - Experience with PowerBI or similar data visualization tools - Knowledge of IT infrastructure and system administration basics - Strong analytical mindset and critical thinking - Basic understanding of cybersecurity principles Why Join Sasol? Sasol is more than an employer — it’s a growth partner. The company’s diversity and inclusion culture, along with its commitment to empowering individuals, ensures that all team members are supported in their career journeys. As a leader in chemical and energy innovation, Sasol opens doors to exciting projects, skilled mentors, and long-term development opportunities. Benefits of the Learnership Programme Include: - Real workplace exposure - Skill development in a Fortune Global 500 company - Mentorship from industry professionals - Certificate of completion upon successful participation - Stipend and travel allowance (if applicable) - Inclusive and supportive working environment 2. Learner Administration: Finance Listing Reference: Req no: 8395Listing Status: Open Position Summary Company: SasolIndustry: Integrated Chemicals and EnergyJob Category: Learnership / Entry-Level TrainingLocation: Sandton, Secunda, Sasolburg, Durban – South AfricaContract Type: Fixed Term (12 Months)Remuneration: Market-related StipendEE position: Yes – Preference to people living with disabilitiesClosing Date: 17 April 2025 Introduction Sasol, a leading global integrated chemicals and energy company rooted in over 70 years of innovation, is offering a unique Learnership opportunity in Finance Administration. With a strong focus on transformation, inclusion, and growth, Sasol aims to empower the next generation of South African talent through structured workplace exposure and academic learning. This opportunity is especially designed for young individuals looking to kick-start their careers in finance, accounting, and business operations. If you’re eager to learn, passionate about finance, and ready to contribute to a dynamic organization, then this 12-month learnership is the right step for you. Job Description The Learner Administration: Finance Learnership is a comprehensive training and development programme that blends practical workplace exposure with academic learning. The programme is structured to provide entry-level candidates with a foundational understanding of finance administration, combined with vital business and communication skills. The learnership consists of: - A theoretical component aligned to a registered NQF Level qualification - Practical on-site work experience at Sasol offices in Sandton, Secunda, Sasolburg, or Durban - Development of foundational skills in literacy, numeracy, communication, and business software Participants will assist with general finance administrative duties, supporting departmental managers and gaining critical experience in various accounting and financial processes. Ideal Candidate Sasol is seeking candidates who are: - Youthful and passionate about finance, accounting, or auditing - Eager to learn and ready to commit to a 12-month structured programme - Living with a disability (preference given as per Sasol's Employment Equity Plan) - Residing in or willing to relocate to Sandton, Secunda, Sasolburg, or Durban Minimum qualification: - Matric / Grade 12 Certificate - A Diploma or Bachelor’s Degree in Finance-related fields is advantageous, especially with majors in: - Financial Accounting - Management Accounting - Taxation - Auditing Experience: - 0 to 1 year of relevant work experience Role Responsibility During the learnership, learners will be responsible for: - Providing day-to-day administrative support within the finance department - Assisting in document management and data entry, - Supporting financial reporting, processing, and reconciliations - Contributing to the implementation of policies and procedures - Participating in departmental planning and workflow coordination - Demonstrating accountability in all tasks assigned Skills & Attributes Technical Competencies: - Workflow Management - Action Planning - Policies and Procedures Knowledge - Execute and Coordinate Work - Performance Improvement Behavioural Competencies: - Nimble Learning - Self-Development - Manages Complexity - Demonstrates Self-Awareness - Ensures Accountability Soft Skills Developed During the Programme: - Communication Skills - Business Writing - Microsoft Office & Computer Literacy - Basic Business Operations - Entrepreneurship - Maths Literacy Why Join Sasol? Sasol is more than just a workplace — it’s a platform for growth. When you join Sasol’s learnership programme, you’re not only gaining hands-on experience but becoming part of a legacy that’s focused on sustainable innovation and excellence in the energy and chemicals sector. Key benefits of joining the Sasol Learnership Programme: - Hands-on experience with seasoned professionals in a real-world finance environment - Structured learning to help you build the skills and knowledge required to succeed - Diversity & Inclusion: Be part of an inclusive culture that values every individual - Career Development Support: Learn from experienced mentors, access internal job opportunities, and build a professional network Click here to Apply Read the full article

[jarviscodinghub]

Math 232 – Computing Assignment 1 solution

1. Part 1 – Solutions of systems of linear equations • By considering random matrices of appropriate sizes, find “emperical evidence” that substantiate the following statements. (In this part, m and n are both integers and both are greater than 6, so 7 or larger). (a) A system of n linear equations in n unknowns typically has a unique solution. (b) A system of m linear equations in n unknowns,…

[maryellencarter]

I don't know shit about stochastic matrices or Markov chains (the types of math that the tags suggest using for this), but I like probability and I'm curious how far I can get with brute force stubbornness.

On day 1, Snart has a 50% chance of staying at the snarting point (H) and a 50% chance of going to point A.

On day 2, if Snart stayed at the snarting point on day 1, he again has a 50% chance of staying put or a 50% chance of going to point A, and the same will be true for as long as he stays there. So we can calculate that the probability of Snart staying at the snarting point for all 5 move chances is 50% raised to the power of the number of days, or to put it in an easier to read format, 0.5 to the 5th power (I am not trying to put an exponent in a Tumblr post). That is, 0.5 * 0.5 * 0.5 * 0.5 * 0.5, or one-32nd, or about 3.1%.

However, this is not the same as the probability that Snart can be found at the snarting point. Let's continue.

If, on day 1, Snart has gone to point A (which you recall he had a 50% chance to do), then on day 2, Snart has a one-fourth chance each to go to point B, C, back to H, or stay at point A. I *think* we can now begin to construct -- I may be reinventing a Markov chain here, it's certainly something I'd name a chain if I was naming it -- a string of five multipliers which will eventually give us the probability of Day 5 Snart at each point. That is, we can take the string of 0.5's that I wrote out above, and substitute whatever Snart's probability of moving or staying is on each date, and construct such a chain for each separate string of possibilities. We might need a lot of scratch paper.

So each string starts with 0.5 because the probability of staying at the snarting point or moving is 50% each way. But on the string where Snart has gone to Point A on day 1, the day 2 string looks thusly: 0.5 * 0.25 * ?? * ?? * ?? because he has a 25% chance of going to (or staying at) each possible point.

So now we need four different possible strings for day 3. If Snart goes back to H on day 2, then on day 3 his options are again staying at H or going to A, giving a day 3 string of 0.5 * 0.25 * 0.5 * ?? * ??

If Snart stays at point A on day 2, his day 3 string is 0.5 * 0.25 * 0.25 * ?? * ?? because he still has the same choices he had on day 2.

If he goes to point B on day 2, then his day 3 choices are staying at B, going back to A, or going to G, each at a one-third probability, which I will round to 0.33 because I am also not putting a "repeating" symbol in a tumblr post. This gives a day 3 string of 0.5 * 0.25 * 0.33 * ?? * ??

If Snart goes to point C on day 2, then on day 3 he again has 4 choices each with a 25% probability: stay at C, go back to A, or go to D or E.

This is where brute force starts to fall down, because now we need strings for every possibility of... let's see, I also need a short way to write the possibilities, this might be the part where I reinvent a stochastic matrix, whatever that is...

Okay, if Snart stayed at the snarting point for all five days, that is pattern HHHHH, and we calculated that it comes out to about 3.1%. (3.125% specifically, but because we have repeating decimals in here anyway, I'm just going to round to 2 significant figures consistently.)

So the other patterns we have started (snarted) setting up so far are, let's see... ooh, it might be easier to calculate some of them from the *end*. Let us consider pattern HHHHA, where Snart moves only once, on day 5, and must move to point A because that's the only point available from H. This will also have a 3.1% probability. I think that's the only other possible pattern to have all 0.5's.

Other possible patterns, let's see -- any pattern that snarts with H must go through A to get anywhere else, so we can construct hypothetical patterns HA???, HHA??, and HHHA?.

Let's see. If we say for argument's sake, to estimate the maximum possible number of permutations because of course this doesn't follow basic permutation rules, if we suppose Snart goes each day to the available point with the maximum choices, that is pattern ACEEE, and it will have the string 0.5 * 0.25 * 0.2 * 0.2 * 0.2, but more relevantly right now, that tells us we need a tree of 2 branches for day 1 (H vs A), 4 branches on one side and 2 on the other for day 2 (HH/HA vs AH/AA/AB/AC), then day 3 can have a *maximum* of... no, wait, is that the wrong question... okay, day 3 can have HHH, HHA, HAH, HAA, HAB, HAC, AHH, AHA, AAH, AAA, AAB, AAC, ABA, ABB, ABG, ACA, ACC, ACD, ACE, I think that's it? That's nineteen. I might need more scratch paper. Or any scratch paper.

Let's see if we can get through day 4. HHHH, HHHA, HHAH, HHAA, HHAB, HHAC, HAHH, HAHA, HAAH, HAAA, HAAB, HAAC, HABA, HABB, HABG, HACA, HACC, HACD, HACE, AHHH, AHHA, AHAH, AHAA, AHAB, AHAC, AAHH, AAHA, AAAH, AAAA, AAAB, AAAC, AABA, AABB, AABG, AACA, AACC, AACD, AACE, ABAH, ABAA, ABAB, ABAC, ABBA, ABBB, ABBG, ABGB, ABGG, ABGE, ABGF, ACAH, ACAA, ACAB, ACAC, ACCA, ACCC, ACCD, ACCE, ACDC, ACDD, ACDE, ACEC, ACEE, ACED, ACEF, ACEG. Jesus murphy. That's 65 permutations. I'm not sure I'm crazy enough to compute this by hand. I'm going to post this much now, to reduce the chances of tumblr eating it while I'm working.

did they ever find Snart btw

[effortentries]

Chicken tikka masala and lil bits about my life story so far.

The first recipe i have decided to attempt is Chicken tikka masala. I got the recipe from tiktok and i can say that it tastes extremely delicious. My dad even said that he would pay me to make it again for him.

For all of the recipes i’m going to add the recipe, the method i used to make the food and also a little bit about my life.

So let’s start this journey

Bismillah

Chicken tikka masala (tiktok version)

ingredients

2 Chicken breasts, cubed

Chicken marination:

1 Tbsp paprika

1 tsp cumin

1 tsp coriander

1 tsp garam masala

1 tsp red chili powder

1/2 tsp tumeric

1/2 tsp salt

2 large spoons yogurt

1/2 tsp garlic ginger paste

the juice of half a lemon

Set aside overnight or for a minimum of 4 hours.

Half an onion, finely chopped

Method

Cook chicken on medium heat in oil

Remove chicken from the pan and add it to a different bowl to rest while the sauce is being made.

Add onions to the pan

Add 3 large spoons of tomato paste

Add half a cup of water

Add one cup of cream

Stir the above ingredients together

Add the spices

1tsp of red chili

1 tbsp of paprika

1tsp of cumin

1 tsp of coriander

1 tsp of garam masala

1/2 tsp of black pepper

1/2 tsp tumeric

Cook all in medium heat until the mixture bubbles and the spices stop being raw.

Add the chicken back in and put the pan on low heat and incorporate everything together.

Garnish with dhanya and enjoy :)

And here begins my first story.

I was raised in a loving home. My most beautiful memories are with my mom, she’d do my hair into all different kinds of hairstyles when i was little, they always had to have cute little “goggles” as she’d call them at the ends of them. She’d plait my hair every day. And put little plastic flowers, or whatever pretty looking thing at the end of them.

I grew up Christian, my parents used to regularly attend an Afrikaans church close to tygerberg high school, and if they didn’t, then gospel songs would ring out every sunday from the TV and little me knew all the words.

Primary school, i kept the nice hairstyles until my mom said i was old enough to do my hair myself. Endless alice bands. I was obsessed with alice bands. I was extremely academically inclined, i was third in the grade in grade 5, grade 6 i was seventh in the grade and grade 7 i was fifth in the grade. I was a monitor for the primary school passages, patrolling all around to tell naughty little boys to tuck their shirts in and to walk in a single file line. I was in the representative council of learners where i’d run meetings, patrol every day during breaks around the school while hoping that all i was doing was enough for me to get into Rhenish girls high. It was.

I accidentally forgot a little part, well…not so little, In grade R i did ballet, then i decided to do the 360° switch to karate after i watched the karate kid for the first time. I carried on with karate throughout primary school.

Now, Rhenish girls high.

Driving to stellenbosch from brackenfell everyday was a challenge, tiring bus rides, but i knew that the education that i’d get at that school would be worth it all. And it was.

I got my black belt when i was in grade 9, i ended up quitting karate because balancing school, and it ended up being a challenge as my sensei wanted me to teach some classes to little children as well.

Grade 10 i dropped pure math, i begged my dad to do that, he looked like he wanted to cry but the decision was worth it in the end. Grade 10 was also when i went with raadiah to her Islamic society meetings, just as an observer.

Grade 11. A busy year, i was captain of 2nd team soccer. i was elected into the matric dance committee. That’s when my journey with graphic design began. I attended more islamic society meetings. I helped raadiah with hijab day, when i put the scarf on my head for the first time i somehow knew where my life would end up. End of grade 11 i was elected into the learner council.

Grade 12 i was…extremely busy? too busy? I was the school’s designated graphic designer, i converted to islam in january of that year so i was still learning a lot, I studied hard. I ended up with 6 distinctions Alhamdulilah. I had full academic colors, and full colors for culture since i did choir for all 5 years of high school

January of 2023 i was left to decide on UCT or Stellenbosch.

UCT offered me a scholarship for Bachelor of social sciences, i was also accepted for LLB but no scholarship for that.

Stellenbosch accepted me for BA law (my dream course), and seemingly didn’t give me a scholarship (they did, but their systems were so bad they only sent the money in may).

I picked stellenbosch, it was home.

Anyways, the food tasted amazing, my parents keep on asking it to make it again.

Maybe aunty can teach me how to make it taste better?

Next time, i’m going to speak about my revert story.

[faurdani]

Neeeerd time!!✨️ (wow it's my 10th months of grad study)

My mood is very good now since today's exam grade is better than I expected alhamdulillah.🤍 so i want to talk about... related to this course: Applied Math I. And other courses actually. I reaaally love that the grad courses connect each other very well!

Actually, this starts from an uneasy feeling I felt in my undergrad. There was a lot of things taught in my undergrad, but I don't understand most of them. And I am very serious. I felt my undergrad is very weird, at least for me. It was so difficult to understand things. I think I did my exams very bad. But the worse thing (to me), is, we did not get any feedback unless the semester is finished.

I hated it because I did not know whether my understanding is correct or not. I didn't know which part is true and which part is not. Whether I did good or bad in midterm, quiz, finals, or homework. I didn't really read the books. I only read Calculus, some Atomic Physics, Feynman for optics & electromagnetics, and books + papers for thesis. Oh, also some parts of book for Sensors, Actuators, Electrical Circuit. The rest.. I just read the prof's ppt/modules. Hahaha ok I admit that I wasn't that "good" in studying.

So I was so lost in Chemistry, Thermodynamics, Heat & Mass Transports, Process Techniques, & Fluid Mechanics. I also felt lost in Linear Algebra, Calculus, Differential Equation, Electronics, Signal Processing, Acoustics, System Dynamics, Controls... (really, I am actually bad... i don't understand how did they grade, why do i still get good grades when I actually don't understand things..)

I might be able to solve the problems from Linear Algebra, Differential Equations, and System Dynamic class back then.

But I didn't understand things. I just followed the pattern, nothing sticked, nothing feels connected.

That's why I was so struggled in the last years of my undergrad: when I faced Instrumentation System Design and Undergrad Thesis--which was about acoustics, mechanics, PDEs.

Many concepts were fixed and got better during the thesis, but I still felt something is missing.

When I first came here (my grad campus), we were tested on 3 subjects, undergrad level: (1) math, (2) physics, (3) chemistry.

Basically that. I passed physics & (surprisingly) chemistry, but failed math, so I should take undergrad level math in my first semester. But I am so happy!

Maybe it's also because I already finished undergrad (so I have some basics, even though it's not strong), maybe the prof is just very good at teaching (the attitude is very great. She is always punctual, effective, and willing to answer every questions. Very helpful). Maybe the ppt, the reference book, the homeworks & quiz are good. Maybe the syllabus, and the curriculum--because at the same time I need to practice a lot of calculus at Fluid Mechanics class. Maybe also the language? I am not so good in English, but now if I think about it... i feel that Indonesian math terms are not intuitive. :") Afterall, maybe it's the combination of that. I love it alhamdulillah. :')

Sooo. In my grad study, I've been taking:

- undergrad math: derivatives, integrals, ODE, series & sequence

- fluid mech: (1) a bit of surface tension, dimensionless analysis, Reynold Transport Theorem, Navier Stokes, vorticity, ideal flow, gravity waves, laminar flow; (2) boundary layer, instability, turbulence, compressible flow (shockwaves); (math) kronecker delta, levi-civita, a looot of PDE & calculus because Navier-Stokes, diff coordinates (cartesian, polar), slight complex for waves & instability discussion

- thermo: 1st, 2nd, 3rd law of thermo; (math) basically PDE *note: i'm still very bad at this*

- solid mech: statics, kinematics, constitutive equations (relating statics & kinematics--basically how to solve/model the solid mechanics phenomenon? --> including elasticity, optimization problem), crack propagation; (math) tensor calculus (dyadic notation, matrices, linear algebra), ODEs, Gauss theorem, diff coordinates (cartesian, cylindrical, polar)

- Applied Math II: complex analysis (complex algebra, derivative, integration, Laurent series) & linear algebra (vectors, dimensions, rank, linear dependency, eigenvalues, eigenvectors. Basically how to solve linear "discrete" system)

- Applied Math I: ODE, PDE. Including Green's Function (transfer function) & Sturm Liouville's problem (eigenvalues, eigenfunctions, linear dependency. How to solve linear "continuous" system)

*phew* that's a lot for one year.

But as you can see... every physics class has some math (generally: calculus, ODE, PDE, linear algebra). It helps me to understand math and math helps me to understand that!

If i remember again, my undergrad has a lot of math also (mainly solving ODE, PDE)..

So that now I'm taking Applied Math I, especially during the Green's function discussion, it blooows my mind!

I rmb very clearly that in undergrad we discussed transfer function *a lot*. It is output per input. But how do we find it?

I didn't understand the math.

In Controls, Acoustics, Instrumentation System Design classes, even for my undergrad thesis, we discussed about harmonic oscillator system.

But i didn't really understand what solution is. Why do we solve that way. Why the transfer function and the solution is written that way.

Now I want to share the main insight from current course. In short (I hope), when we have ODE:

Ly(x) = f(x); L is linear differential operator (e.g. D² + pD + q),

f is the input and y is the output

We can solve this, get a solution of

y(x) = int[ G(x,t)*f(t) ]dt

Such that G, the Green's function is equivalent to output over input; the transfer function. And we practice--G only depends on L and Boundary Conditions!

Moreover,

Ly(x) = f(x) is actually equivalent to

LG(x,t) = delta(x-t); delta(x-t) is impulse at x=t, means we'll get transfer function if we give impulse as the input! (I knew this "physically" but math understanding is ✨️amazing✨️)

And thenn I also just notice (or maybe remember, but now understand by heart, I hope) that impulse is a derivative of step, which is a derivative of smooth piecewise function.

And smooth piecewise function can actually be written as a series. Fourier series.

And Fourier series can also be seen as a linear combination of 3 orthogonal bases: 1, sin(n*pi*x/L), cos(n*pi*x/L). Note that we can imagine 3 orthogonal bases as x,y,z in Cartesian coordinates..

Honestly the concept of relating vectors (matrix, "discrete") with functions ("continuous") amazes me in the beginning of this course. 🥺🥺✨️

[rosesrded]

18.06.2025 (wed)

Sœ, it’s the day before my math exam and all I’ve done is watch a one-shot on Relations and Functions.

I had 3 days of study leave but listen—every other subject gets only one day. So in the name of equality, I simply refused to study until now.

Justice has been served. Period.☝🏻😀

I’ve got the first 6 chapters to cover (basically the whole Part 1 reader), but I think I can pull it off if I stay in the same zone I've been in this morning.

Been sleeping early at 9–10pm and waking at 5–6 AM like yasss ~~ we love jet lag lol

Anyway. I did Matrices. Currently on Continuity & Differentiability.

Our teacher gave us the weightage TODAY, so maybe it’s actually good I procrastinated?? Who knows. Maybe I’m blessed. Maybe I’m delusional

Was in a deep rut the last two days until I cleaned my room and suddenly got my life together.

If you wanna know how I’m doing mentally, check the state of my cupboards. Room can’t be messy for long cuz my parents will whoop ma ass so I just shove everything into the cupboards. Which does wonders on my mental health btw 🤡

Also, I've actually started working out yesterday partly because I’ve been tired 24/7 for literally no reason and I was like maybe its because I don't move my body much yk ? Like I've been thinking about it for a while. And honestly? I kinda love it. Nothing beats feeling the high post-workout, even if I’m lowkey dizzy in the shower. And after. Hopefully soon I’ll feel less like a constantly drained phone battery and more like a functioning human being 💀

Byee ~~

[magnet-lattice]

Some of the notes have brought to my attention that the relevant context for this post is a mix of fairly old videos with recent enough streams that there are not relevant edited YouTube videos available yet, so I will add some clips for explanations and context. (Transcripts below the cut.)

S3 (Ashswag's edited video):

S5 (MinuteTech's abyss arc finale stream):

Clip 1 (S3, Ashswag's issues with Zam's elevator):

Ash, voiceover, accompanied by footage of Ash pressing a button and then lagging and falling through the floor of the redstone elevator as it rises: This elevator has been discriminating against me for several months now. You see, it runs on some really fancy slime-honeyblock redstone that my internet cannot keep up with. Ash, in the footage: I'm gonna get my revenge on this elevator, one way or the other.

Clip 2 (S5, Ashswag learns Bacon wrote the math problem wrong):

Minute: (okay we're back we're back, chat)

Ash: And you know what the worst part is? Bacon-- I just asked Bacon and he said, "oh, yeah I'm sorry, I didn't know that was the symbol for determinants." I swear when I see this guy at VidCon, I swear, somebody hold me back.

Minute: Oh my gosh, oh my gosh.

Ash: When I see this kid at VidCon, somebody hold me back.

Minute: Oh my god.

Ash: It's absolute value. He-- you know what absolute value is, Minute?

Minute: Yeah, yeah--

Ash: Absolute value is if you get a negative number, it's just the number, it's just the positive version, and-- and this kid didn't know that it's the symbol for determinants, he didn't know it's a symbol for magnit[ude]--

Clip 3 (S5, Ash reacting to Bacon's math error with Minute pre-event):

Ash: I hope someone in chat feels my pain. I genuinely do, I don't know how-- I'm lost for words right now. I've played on this server three years: never been this angry. And he's being so like stuck up about it, chat, you don't know--

Minute: Okay, whatever. What do we get, though, what do we get now?

Ash: This is the-- hold on, one second, let me vent for a second.

Minute: Okay.

Ash: This is like the culmination of weeks and weeks of them being like, "oh, why don't you guys just solve the puzzles", "oh why're you guys just complaining, obviously we're going to stall", being like stuck up about their stupid holier-than-thou mission. They're trying to void spawn and they're trying to make us seem like the crazy people. Never let anyone gaslight you into thinking that you're not worth it, chat. That's my advice for today.

Clip 4 (S5, Ash confronts Bacon about the math errors):

Ash: No, Bacon, not a shred of-- you know how much-- bro. I got called a clown in my math gc. I want you to know that. Because you wrote the question wrong.

Bacon: That's so funny. Okay, wait, what did I write wrong? What did I write wrong, I'm actually curious.

Minute: Bro, I don't wanna fucking talk about it, bro, let's just do our epic finale, please! Let's do our epic finale now, please!

Ash: 23^7819, you wrote "2^37819", it's not possible to solve modular arithmetic when the highest common denominator between 26 and 2 is 2, the Euler's totient formula just doesn't work. It just doesn't work. And also the fucking absolute value thing you did? Boy do I have-- dude, matrices? That symbol is for determinant. And you just-- bro--

Bacon: Yeah, no, actually, I'm remembering this now, I haven't done matrix-- I only did, it was like a year ago.

Ash: (Oh my f--) I'm making-- I don't care, you're gonna get hate comments. I'm saying all of this in the video, I'm--

Zam (background): Oh my god.

Bacon: Wait, wait! No, this isn't my fault, though! This is Meep's fault!

Ash: I don't care.

Minute (background, overlapping): Whatever bro, whatever bro, whatever bro, it's done, it's done, it's done, it's done, let's do our cool--

Bacon: The determinant thing was my fault, but unfortunately the other thing is Meep's fault.

♠️.

[rashlin3110]

The Journey to Understanding Data Science

Data science is a fascinating and ever-changing field that helps us make sense of data. In this blog, we'll break down the core areas of study in data science using easy-to-understand language, helping you grasp the basics of this captivating discipline.

1. Mathematics: At the heart of data science is mathematics. Data scientists study statistics, linear algebra, calculus, and probability theory. These math concepts help them find patterns in data, make predictions, and check if their findings are reliable.

Statistics: Data scientists use statistics to understand and analyze data. They look at things like averages, differences, and testing ideas to draw sensible conclusions from data.

Linear Algebra: Linear algebra helps data scientists work with data in an organized way. It uses matrices and vectors for jobs like simplifying data and creating machine learning models.

Calculus: Calculus helps data scientists understand how data changes over time. It's especially useful for making machine learning models and programs work better.

2. Programming: Data scientists study programming languages like Python and R and tools like SQL. These languages help them work efficiently with data.

Python: Python is one of the most common programming languages in data science. It's used to write code for data analysis, making graphs, and creating machine learning models.

SQL (Structured Query Language): Learning SQL is a must for getting data from big datasets. It's all about asking questions and getting answers from databases.

3. Data Cleaning and Preprocessing: A big part of a data scientist's job is making data clean and ready for use. This means fixing things like missing numbers, taking out weird stuff, and making sure the data makes sense.

4. Machine Learning and Data Mining: Data scientists study machine learning and data mining to make models that predict things and find patterns in data.

Supervised Learning: In supervised learning, data scientists use labeled data to make predictions. They can predict things like house prices, what customers will do, or if someone is sick.

Unsupervised Learning: Unsupervised learning helps data scientists find patterns in data without labels. This includes grouping similar things together and making data easier to understand.

5. Domain Knowledge: Domain knowledge means understanding the field you're working in, like healthcare, finance, or marketing. Data scientists need to know the details and problems of that area to get the most value from the data.

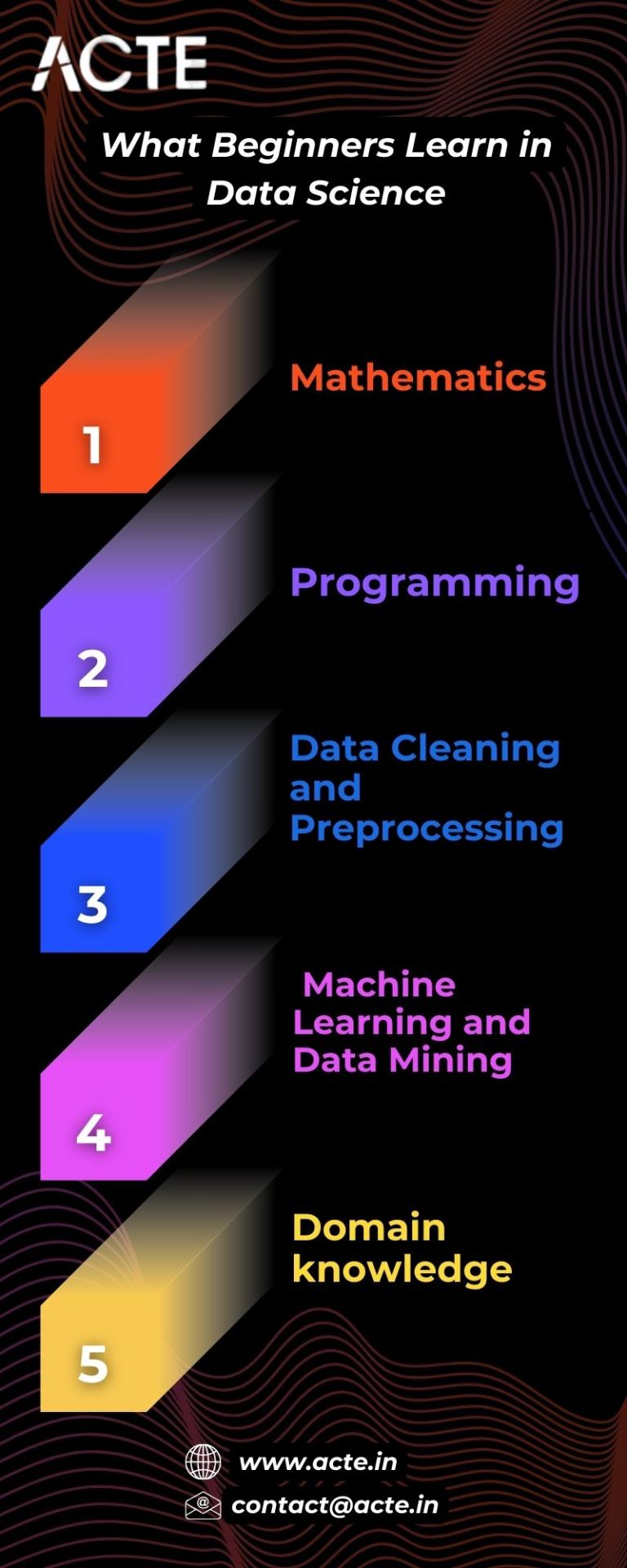
Data science is a mix of math, programming, data cleaning, machine learning, data visualization, and knowing the field you're working in. Data scientists use these skills to explore data, find useful insights, and make smart decisions using data.

If you're interested in learning more about data science course, I'd recommend checking out ACTE Technologies. They offer certifications and help you find job opportunities. Their experienced instructors can make learning easier for you, and you can choose to attend classes either online or in person. If data science piques your interest, you might want to consider taking a course.

I hope this information helps you. If you have any more questions, feel free to ask them in the comments. I'm here to learn and provide assistance. If you found this helpful, please show your support by following me and giving me a thumbs-up. Thanks for your time and support. Have a wonderful day!

[floralfractals]

yes yes yes yes yes these guys are CRAZY

so the story is as follows. suppose youre mr. wigner jenö, a jewish man born in hungary, studied in Germany, fled to the USA because of the whole being-jewish-in-1930s-germany thing. youre interested in this new and upcoming field called quantum mechanics, specifically in the context of molecular crystallography. (un)fortunately for you, that means having to delve into mathematics.

in mathematics, quantum processes are usually modelled using hermitian square matrices (meaning: if you mirror them through the main diagonal and take complex conjugates of any entry, you get the same matrix back). to specifically study atoms of heavy elements, wigner introduced the idea of using so-called random matrices. these are real-valued, symmetric, and their entries are distributed according to some kind of distribution. in math terms: a square matrix is a collection of numbers a_{i,j} where i and j range from 1 to n, and he would randomly distribute the a_{i,j} when j is less than or equal to i, and otherwise define a_{i,j} = a_{j,i}.

now for this quantum setting, the interesting part is to look at the eigenvalues related to these matrices. so wigner sets out to his chalkboard, or perhaps uses an old-school computer, and calculates some of those eigenvalues (for this, he picked an easy probability distribution: the entries were either 1 or -1 with equal probability).

first he simulated some 1x1 matrices. 50% of the eigenvalues were -1. and the other half were 1. just as he expected.

then he moved on to 2x2, dividing each entry by sqrt(2) to normalise everything. about 12.5% were 2, 12.5% were -2, and the other values were 0, -sqrt(2) and sqrt(2), each with a probability of 25%. hm.

as he moved on to nxn matrices for bigger and bigger numbers n, normalising by sqrt(n), he got closer and closer to an unexpected pattern:

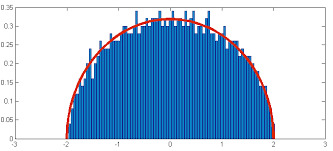
a perfect semicircle of radius 2. surely, thats just a fluke right? the distribution he picked was weird? so maybe he went on to test other distributions (with mean 0, standard deviation 1). and every. single. time. the same picture popped up.

i almost screamed myself when i was doing these same simulations. changing the mean and standard deviation doesnt help either: if the mean is off, exactly 1 eigenvalue breaks off of the rest and goes somewhere else to do its own thang. if the standard deviation is not exactly one, the circle gets a bit smushed into an oval shape.

if youd like to read some more, there are some excellent papers written about this. wigners papers are available themselves of course, as well as some lecture notes from different universities. theres also some great work done that relates this to random graphs and wifi network analysis!

One thing about me is I infodump about math subjects on request

[crazy-pages]

Also I realized this doesn't really answer the question of how particles interact with fields.

I don't know if this will help at all or if it'll just be more confusing, but I'm going to hope this helps!

Math has these things called "groups". A group is made out of a set of elements, typically stuff like numbers or matrices (grids of numbers with certain rules), and an operation on that group like addition or multiplication. There are also other rules of groups, one of which is that if you operate two parts of the group on one another, they have to produce another member of the group.

So this can be something like the set of all integers, and addition. (1+4=5) Or the set of all real numbers (so including fractions and irrationals) and multiplication. (1.4x2=2.8)

Now there's also something called a normal subgroup. This is part of a group's elements. Specifically, it is the elements of a group which, when acted on by any other element of the entire group, stay part of that normal subgroup. The real numbers and multiplication have a normal sub group of just one number, 0! If you multiply 0 by anything, it remains 0! However, there is no normal subgroup of integers and addition (other than the whole group). There is no subset of integers which, when you add any other integer to them, stay in that subset.

Now some groups can be very complicated and they can have very complicated normal subgroups with more than one element in them. And it just so happens that we can describe all of the physical forces of our world with group theory. The electromagnetic force can be described by a group. And this group has an element describing every single possible combination of electromagnetic forces for every single point in space and every single momenta (the direction and degree a point can be moving). All of them! Every single one!

And at any given time, each of those elements can exist or not exist. And you can also describe the way these elements act on one another as time passes. A bit of electric field here changes this bit of magnetic field there, and is in turn transformed into something different itself. The math is very complicated, but also beautifully straightforward in its own way. It's all just a group.

Well, what do you think happens if we go looking for normal subgroups of the electromagnetic field group?

Here's the interesting thing. We will find them! We will find elements of the group which can be transformed, but only into other elements of the same normal subgroup. And these? These are elementary particles.

An electron acted upon by an electric field may change its position. It may change its momentum. It may change its spin, it may change many things! But it remains an electron. And a particle out there in reality is defined by a cloud of elements existing, saying "Yes! Yes there is an electron here, in this point in the cloud, and it exists to this degree (how dense the cloud is) and it has this spin! And if you poke it with electromagnetism it may move and the cloud density may change and the spin May change, but gosh darn it is going to stay an electron!"

Every field, the electromagnetic field, the weak field, the strong field, the higgs field, the gravitational field (*screeching brake noise* well, maybe the gravitational field, we don't fully understand quantum gravity yet), all of these fields have normal subgroups which define their elementary particles.

Now obviously, particles can be destroyed and converted into other forms of energy or matter. This is a bit beyond my formal level of education, but as I understand it this is what happens when different forces interact with one another, or when things get high enough energy that the approximations we use to generate these normal subgroups break down.

So particles interact with fields because they are part of the field! An electron isn't any more or less part of the electromagnetic field than the electric field around it. They are simply special in that they are specific flavors of the field which are difficult to destroy or create.

And the shape these particles take is, as mentioned above, a big fluffy cloud of variable density. But also each point in the field can be treated as a full particle in its own right.

how can elementary particles be points and not like physical things like how is a photon a point in the electromagnetic field (whatever that is) but it can affect it

-

[floralfractals]

OKAY SO i was a linear algebra TA last semester, and we covered the C-H theorem at the beginning somewhere. it's made everything in my life easier and i grab every single excuse i can find to use it. this might be my favourite theorem.

so when you have a matrix, and you wanna manually compute the eigenvalues, you first have to construct the characteristic polynomial. thats the determinant of xI - A (or x - A as a shorthand (if you think about it, the identity is kind of like a 1 so x*1 - A is clearly x - A)), where A is your matrix, I is the identity, and x is variable. you end up with a polynomial P and the zeroes of P are exactly the eigenvalues.

probably most math fans are familiar with this, but lets still do an example since its nice to understand this for the rest of this post. suppose you have this matrix, lets call it A:

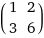
it has (1, 2) on the top row and (3, 6) on the bottom. so xI - A would be the matrix with (x - 1, -2) on the top and (-3, x - 6) on the bottom. the determinant of xI - A is P(x) = (x - 1)(x - 6) - 6 = x^2 - 7x = x(x - 7). thus, the eigenvalues are 0 and 7. easy, right?

ok well lets look at P a little closer. the thing about polynomials is that you can put a lot of different things in the input: in fact, if X is a set where +, -, *, 1 and 0 are well-defined and function as expected, i.e. if X is a ring, then P(x) is defined for any x in X.

the set of n x n matrices is a ring! thus, we can put matrices in our polynomial. lets see what happens if we put in our original matrix. P(A) = A^2 - 7A. well, A^2 is this thang:

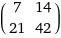
and 7A is... huh, weird, its the same! so P(A) = A^2 - 7A = 0.

now im ready to tell you the Cayley-Hamilton theorem: if you have a matrix A, and if P is the corresponding characteristic polynomial, then P(A) = 0, always.

this comes in handy a lot. you dont think i really calculated A^2 by hand earlier, right? no of course not, i used C-H: if P(A) = A^2 - 7A = 0, then that must mean A^2 = 7A.

ill post this now since its getting long, but theres more to come so ill write out a second part in a separate reblog!

One thing about me is I infodump about math subjects on request