#regressionmodelinginracticep

[regressingnow]

Working with Multiple Regression : W3

Regression Modeling In Practice 3

In the third week of our assignments at Regression Modeling in Practice, we were expected to perform a multiple regression model between an initial explanatory variable from a large dataset, and add several other confounding variables to improve the prediction capabilities.

I continued to use the ‘gapminder’ dataset from last week which provides data about the population, life expectancy and GDP in different countries of the world from 1952 to 2007. Within this large dataset, We already examined a possible relationship between the Per Capita Income in a country versus it’s life expectancy. Now we will look at effect of other confounding variables which could provide a better prediction of the Life Expectancy in the country

Experiment

It is logically expected that a higher income provides access to better healthcare, increases affordability of prescription drugs, and possibly access to better insurance policies, thus improving life expectancy. This was the reason to choose the Per Capita Income as the first explanatory variable. However, there are several other factors in the dataset which might contribute to the life expectancy in a particular country. Factors such as ‘Alcohol Consumption’, ‘Employment Rate’, and ‘Urbanization Rate’ all do definitely affect the life expectancy of a single person and a country as a whole. Let’s examine if the data says the same too. 

Details

Here, the ‘Income Per Person’ is the primary explanatory variable while the ‘Life Expectancy’ becomes the response variable. 

A Linear Regression Model of  ‘Income Per Person’ and  ‘Life Expectancy’ gives the following result :

Mean for Income Per Person 7262.857778727173 Mean for Centered Income Per Person 6.025402399245649e-13

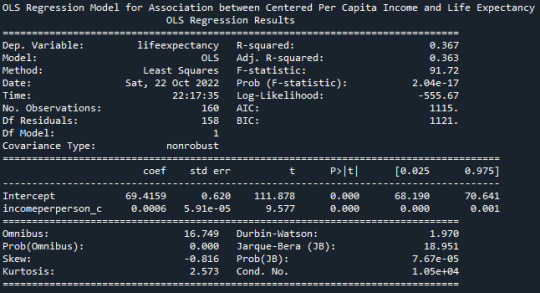
From the R-Squared values reported in the OLS Model, we can understand that about 36.7% of the variance seen in the Life Expectancy can be attributed to the Per Capita Income.

The p-value is very small <0.0001, this indicating that the null hypothesis can be rejected. There is indeed a significant effect of Per Capita Income on the Life Expectancy. Beta is 0.0006.

Life Expectancy = 0.0006*(Centered Income Per Person)+72.2992 

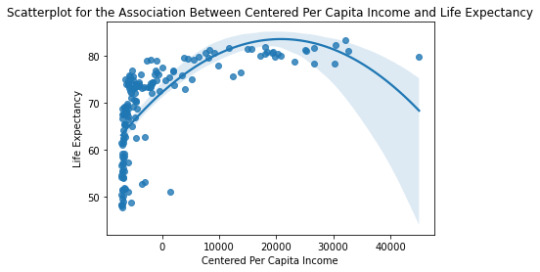
However, a plot between the Per Capita Income and Life Expectancy does not show a great agreement between the model prediction and available data, especially at lower Per Capita Income (PCI).

Scatter for the Linear association between Life Expectancy and PCI

Using  a 2nd order Quadratic Regression Model for the same two variables, we get the following result :

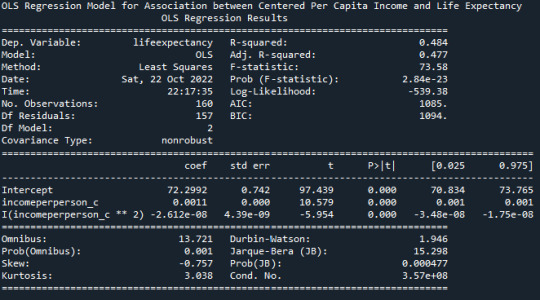
We get a better R-Squared value reported in the OLS Model of 0.484, thus proving a better fit, as seen in the plot below. Beta value of 0.0011 is also to be noted.

The p-value is very small <0.0001, this indicating that the null hypothesis can be rejected. There is indeed a significant effect of Per Capita Income on the Life Expectancy.

Life Expectancy = -2.6e-8*( (Centered Income Per Person)^2 + 0.0011*(Centered Income Per Person) + 72.299

We will retain this quadratic relationship for the Multiple Regression too

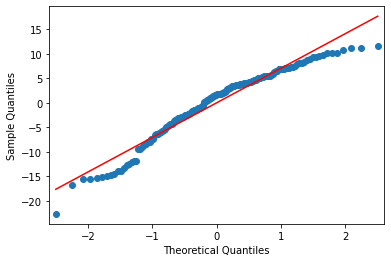
Below is the qq-plot for the quadratic regression model. There are some outliers at the lower and higher ends of the data.

And here is the residual plot. There are more outliers towards the negative residuals but not significantly high.

Let us now analyze ‘Alcohol Consumption’ as the first confounding variable while the ‘Life Expectancy’ becomes the response variable.

A Linear Regression Model of  ‘Alcohol Consumption’ and  ‘Life Expectancy’ gives the following result :

Mean for Alcohol Consumption 6.824312499999998 Mean for Centered Alcohol Consumption 2.2398749521812534e-15

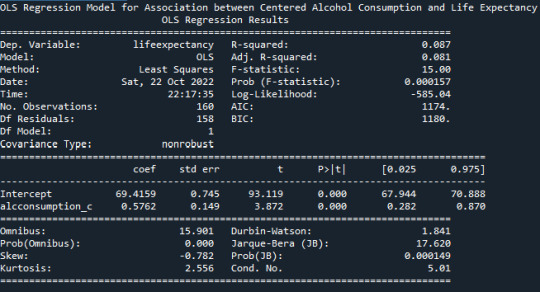
From the R-Squared values reported in the OLS Model, we can understand that about 8.7% of the variance seen in the Life Expectancy can be attributed to the Alcohol Consumption. There is a positive-Beta value of 0.5762

The p-value is very small <0.0001, this indicating that the null hypothesis can be rejected. There is indeed a significant effect of Alcohol Consumption on the Life Expectancy.

Life Expectancy = 0.5762*(Centered Alcohol Consumption)+69.4159

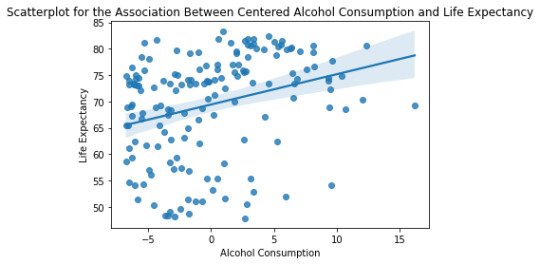
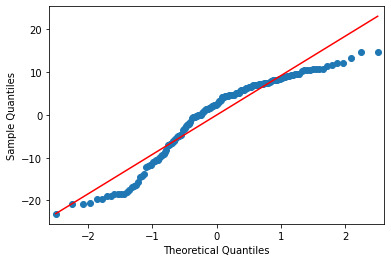
Below is the qq-plot for the quadratic regression model. Some of the lower outliers from the previous case are better accounted here.

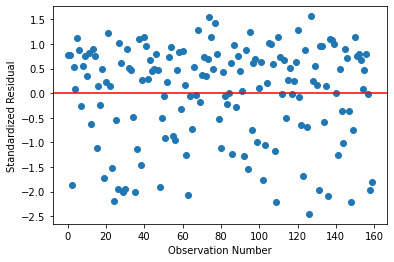
And once again the residual plot is as below. Once again,  there are more outliers towards the negative residuals but not significantly large number.

Let us now further analyze ‘Employment Rate’ as the second confounding variable while the ‘Life Expectancy’ becomes the response variable.

A Linear Regression Model of  ‘ Employment Rate ’ and  ‘Life Expectancy’ gives the following result :

Mean for Employment Rate 59.076875066757204 Mean for Centered Employment Rate -5.773159728050814e-16

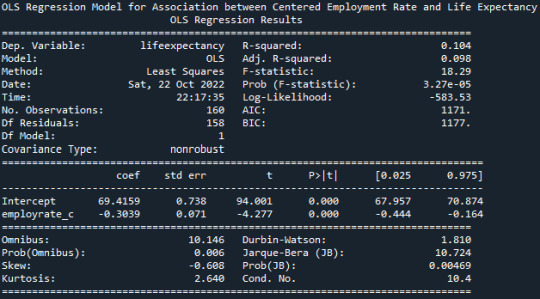
From the R-Squared values reported in the OLS Model, we can understand that about 10.4% of the variance seen in the Life Expectancy can be attributed to the Alcohol Consumption. There is a negative-Beta value of 0.3039, suggesting that the Life Expectancy decreases with the Employment Rate.

The p-value is very small <0.0001, this indicating that there is indeed a significant effect of Employment Rate on the Life Expectancy.

Life Expectancy = -0.3039*(Centered Employment Rate)+69.4159

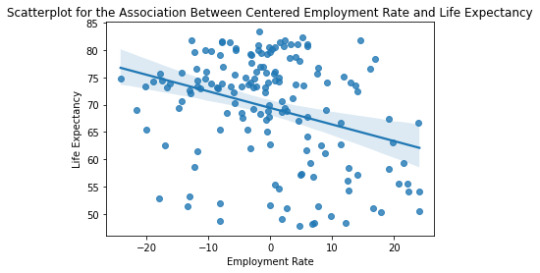
Below is the qq-plot for the quadratic regression model. Again some of the lower outliers from the previous case are better accounted here., and it has a better agreement along the center portion too

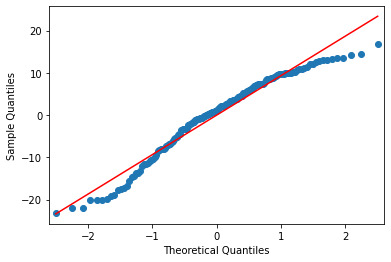
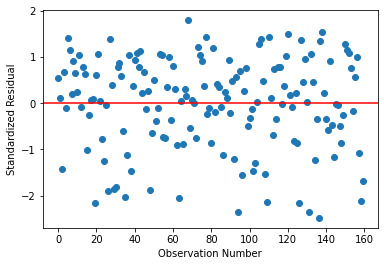
Here is the corresponding Residual Plot

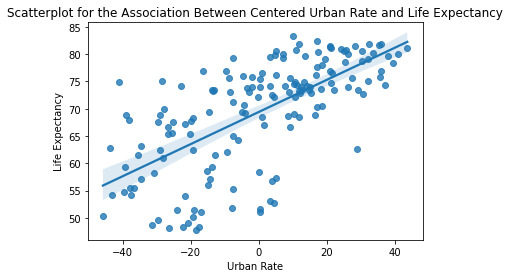
Finally, et us  analyze ‘Urbanization Rate’ as the last confounding variable while the ‘Life Expectancy’ becomes the response variable.

A Linear Regression Model of  ‘Urbanization Rate ’ and  ‘Life Expectancy’ gives the following result :

Mean for Urban Rate 56.278125 Mean for Centered Urban Rate -2.3092638912203257e-15

From the R-Squared values reported in the OLS Model, we can understand that about 44% of the variance seen in the Life Expectancy can be attributed to the Alcohol Consumption. There is a positive-Beta value of 0.2940.

The p-value is very small <0.0001, this indicating that there is indeed a significant effect of Urbanization Rate on the Life Expectancy.

Life Expectancy = 0.2940*(Centered Urbanization Rate)+69.4159

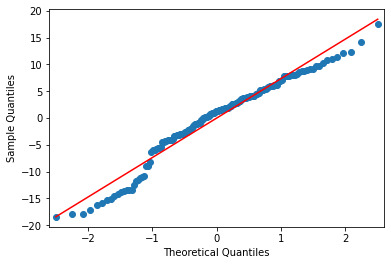
Below is the qq-plot for the quadratic regression model. This is one of the best agreements seen in this analysis.

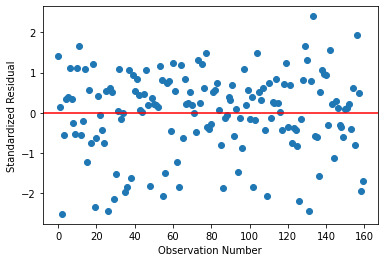
And once again, the corresponding Residual Plot. As suggested by the fit, the outliers are also limited with this model.

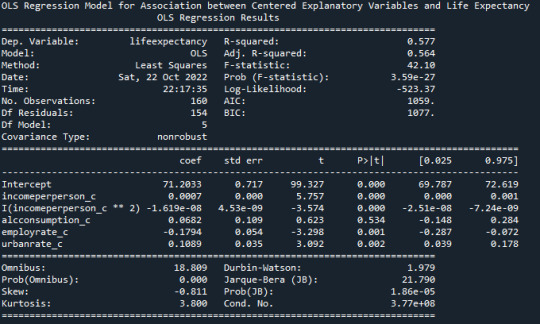
Multiple Regression Model using the above variables for ’Life Expectancy’ Response Variable

Using the above gathered variables, both explanatory and confounding, in a multiple regression analysis, we get the following output

Evaluating the Model Fit for all the variables, we see the following

From the P-values (P < 0.05) for each of the individual explanatory and confounding variables, it is evident that Income per Person (Beta = 0.0007), Employment Rate (Beta = -0.1794) , and Urbanization rate  (Beta = 0.1089) ave a strong association with the Life Expectancy in a country. However, Alcohol Consumption (P-Value > 0.05) has no effect on the Life Expectancy. The overall R-Squared value of 0.577 indicates that about 57.7 percent of the variance in the Life Expectancy can be explained by the Per Capita Income, Employment Rate, and Urbanization Rate.

The qq plot below, for the multiple regression continues to show outliers at the lower and upper ends, but shows a pretty agreement otherwise.

Below is the residual plot from Multiple Regression Analysis. Much of the residuals do lie within 1 standard deviation, while some are present between -1 and -2 standard deviation too. The fit could be made better by the addition of other explanatory variables.

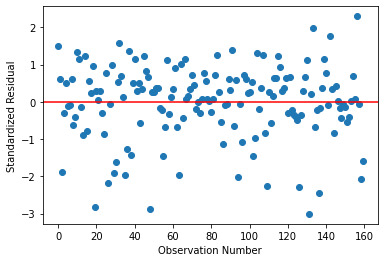
Below is the Leverage Plot for the Multiple Regression Model. This plot also tells us that the outliers have small or close to zero leverage values, meaning that although they are outlying observations, they do not have an undue influence on the estimation of the regression model. The one observation that has a large leverage on the model is however not an outlier.

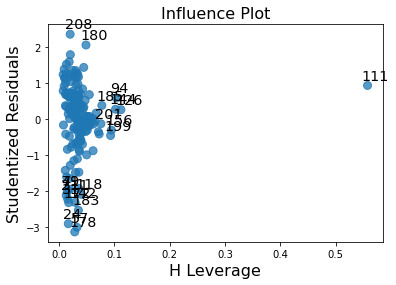
Thus, we have successfully formulated a Multiple Regression Model that can explain upto 60% of the variance in Life Expectancy using a combination of explanatory variables.

Below is the Code that was used to generate these results :

mainset[["employrate_c"]]=mainset[["employrate"]]-mainset[["employrate"]].mean() mainset[["urbanrate_c"]]=mainset[["urbanrate"]]-mainset[["urbanrate"]].mean()

#Collecting the Variables ppincome = mainset.incomeperperson ppincome_c = mainset.incomeperperson_c alcohol = mainset.alcconsumption alcohol_c = mainset.alcconsumption_c co2emit = mainset.co2emissions co2emit_c = mainset.co2emissions_c emprate = mainset.employrate emprate_c = mainset.employrate_c urbrate = mainset.urbanrate urbrate_c = mainset.urbanrate_c lifeyears = mainset.lifeexpectancy

#Basic Linear Regression with centered Income Per Person print ("Mean for Income Per Person") meanppi = ppincome.mean() print(meanppi) print ("Mean for Centered Income Per Person") meanppi_c = ppincome_c.mean() print(meanppi_c)

#Basic Linear Regression with centered Income Per Person (Linear) print('OLS Regression Model for Association between Centered Per Capita Income and Life Expectancy') reg1 = smf.ols('lifeexpectancy ~ incomeperperson_c',data=mainset).fit() print(reg1.summary())

#Plotting the explanatory centered Income Per Person and Life Expectancy (Linear) scat1 = seaborn.regplot(x="incomeperperson_c", y="lifeexpectancy", scatter=True, data=mainset) plt.xlabel('Centered Per Capita Income') plt.ylabel('Life Expectancy') plt.title ('Scatterplot for the Association Between Centered Per Capita Income and Life Expectancy') print(scat1)

#Basic Quadratic Regression with centered Income Per Person print('OLS Regression Model for Association between Centered Per Capita Income and Life Expectancy') reg2 = smf.ols('lifeexpectancy ~ incomeperperson_c+ I(incomeperperson_c**2)',data=mainset).fit() print(reg2.summary())

#Plotting the explanatory centered Income Per Person and Life Expectancy (2nd Order) scat2 = seaborn.regplot(x="incomeperperson_c", y="lifeexpectancy", scatter=True, order =2, data=mainset) plt.xlabel('Centered Per Capita Income') plt.ylabel('Life Expectancy') plt.title ('Scatterplot for the Association Between Centered Per Capita Income and Life Expectancy') print(scat2)

#Q-Q plot for normality fig1=sm.qqplot(reg2.resid, line='r')

# simple plot of residuals stdres1=pd.DataFrame(reg2.resid_pearson) plt.plot(stdres1, 'o', ls='None') l = plt.axhline(y=0, color='r') plt.ylabel('Standardized Residual') plt.xlabel('Observation Number')

#Basic Linear Regression with centered Alcohol Consumption print ("Mean for Alcohol Consumption") meanalc = alcohol.mean() print(meanalc) print ("Mean for Centered Alcohol Consumption") meanalc_c = alcohol_c.mean() print(meanalc_c)

#Basic Linear Regression with centered Alcohol Consumption (Linear) print('OLS Regression Model for Association between Centered Alcohol Consumption and Life Expectancy') reg3 = smf.ols('lifeexpectancy ~ alcconsumption_c',data=mainset).fit() print(reg3.summary())

#Plotting the explanatory centered Alcohol Consumption and Life Expectancy scat3 = seaborn.regplot(x="alcconsumption_c", y="lifeexpectancy", scatter=True, data=mainset) plt.xlabel('Alcohol Consumption') plt.ylabel('Life Expectancy') plt.title ('Scatterplot for the Association Between Centered Alcohol Consumption and Life Expectancy') print(scat3)

#Q-Q plot for normality fig2=sm.qqplot(reg3.resid, line='r')

# simple plot of residuals stdres2=pd.DataFrame(reg3.resid_pearson) plt.plot(stdres2, 'o', ls='None') l = plt.axhline(y=0, color='r') plt.ylabel('Standardized Residual') plt.xlabel('Observation Number')

#Basic Linear Regression with centered Employment Rate print ("Mean for Employment Rate") meanemp = emprate.mean() print(meanemp) print ("Mean for Centered Employment Rate") meanemp_c = emprate_c.mean() print(meanemp_c)

#Basic Linear Regression with centered Emplotment Rate (Linear) print('OLS Regression Model for Association between Centered Employment Rate and Life Expectancy') reg4 = smf.ols('lifeexpectancy ~ employrate_c',data=mainset).fit() print(reg4.summary())

#Plotting the explanatory centered Empoyment Rate and Life Expectancy scat4 = seaborn.regplot(x="employrate_c", y="lifeexpectancy", scatter=True, data=mainset) plt.xlabel('Employment Rate') plt.ylabel('Life Expectancy') plt.title ('Scatterplot for the Association Between Centered Employment Rate and Life Expectancy') print(scat4)

#Q-Q plot for normality fig3=sm.qqplot(reg4.resid, line='r')

# simple plot of residuals stdres3=pd.DataFrame(reg4.resid_pearson) plt.plot(stdres3, 'o', ls='None') l = plt.axhline(y=0, color='r') plt.ylabel('Standardized Residual') plt.xlabel('Observation Number')

#Basic Linear Regression with centered Urban Rate print ("Mean for Urban Rate") meanurb = urbrate.mean() print(meanurb) print ("Mean for Centered AUrban Rate") meanurb_c = urbrate_c.mean() print(meanurb_c)

#Basic Linear Regression with centered Urban Rate (Linear) print('OLS Regression Model for Association between Centered Urban Rate and Life Expectancy') reg5 = smf.ols('lifeexpectancy ~ urbanrate_c',data=mainset).fit() print(reg5.summary())

#Plotting the explanatory centered Urban Rate and Life Expectancy scat5 = seaborn.regplot(x="urbanrate_c", y="lifeexpectancy", scatter=True, data=mainset) plt.xlabel('Urban Rate') plt.ylabel('Life Expectancy') plt.title ('Scatterplot for the Association Between Centered Urban Rate and Life Expectancy') print(scat5)

#Q-Q plot for normality fig4=sm.qqplot(reg5.resid, line='r')

# simple plot of residuals stdres4=pd.DataFrame(reg5.resid_pearson) plt.plot(stdres4, 'o', ls='None') l = plt.axhline(y=0, color='r') plt.ylabel('Standardized Residual') plt.xlabel('Observation Number')

#Multiple Regression with centered Variables print('OLS Regression Model for Association between Centered Explanatory Variables and Life Expectancy') reg6 = smf.ols('lifeexpectancy ~ incomeperperson_c+ I(incomeperperson_c**2)+alcconsumption_c+employrate_c+urbanrate_c',data=mainset).fit() print(reg6.summary())

#Q-Q plot for normality fig5=sm.qqplot(reg6.resid, line='r')

# simple plot of residuals stdres5=pd.DataFrame(reg6.resid_pearson) plt.plot(stdres5, 'o', ls='None') l = plt.axhline(y=0, color='r') plt.ylabel('Standardized Residual') plt.xlabel('Observation Number')

# leverage plot fig6=sm.graphics.influence_plot(reg6, size=8) print(fig6)

# additional regression diagnostic plots fig7 = plt.figure(figsize=(12,8)) fig7 = sm.graphics.plot_regress_exog(reg6,  "incomeperperson_c", fig=fig7)

fig8 = plt.figure(figsize=(12,8)) fig8 = sm.graphics.plot_regress_exog(reg6,  "employrate_c", fig=fig8)

fig9 = plt.figure(figsize=(12,8)) fig9 = sm.graphics.plot_regress_exog(reg6,  "urbanrate_c", fig=fig9)

fig10 = plt.figure(figsize=(12,8)) fig10 = sm.graphics.plot_regress_exog(reg6,  "alcconsumption_c", fig=fig10)