#solving linear inequations in one variable | Explore Tumblr posts and blogs

mark007william · 2 years ago

Text

Master Algebra with the Best Algebra Calculator

Algebra, often dubbed the "gateway to higher math," is a foundational subject that plays a crucial role in mathematics education. It serves as a bridge between basic arithmetic and more advanced mathematical concepts. While mastering algebra is essential for success in various fields, it can be a challenging journey for many students. However, the advent of technology has brought forth a valuable tool: the algebra calculator. In this blog, we will explore how you can master algebra with the best algebra calculator at your side.

While algebra calculators serve as fantastic tools for mastering algebra, the guidance and expertise of professionals cannot be understated. My Assignment Help Expert understands the challenges that students face when tackling algebraic concepts and equations. Their team of experienced educators and mathematicians not only provides assistance in algebra but also offers personalized support to help you understand the underlying principles.

The Algebra Conundrum

Algebra is all about using symbols, letters, and numbers to represent and solve real-world problems. It introduces you to essential concepts like equations, inequalities, variables, and functions. Despite its importance, algebra can be intimidating for some, often due to:

Complex Equations: Dealing with equations that involve multiple variables and unknowns can be daunting.

Abstract Notation: The use of abstract symbols, such as "x" and "y," can be confusing, especially when transitioning from straightforward arithmetic.

Problem Solving: Algebra challenges your problem-solving skills, requiring you to apply rules and methods to find solutions.

Conceptual Understanding: Understanding the underlying principles and concepts in algebra is crucial for applying them effectively.

The Role of Algebra Calculators

Algebra calculators, often available as software applications or online tools, provide valuable assistance in your algebraic journey. Here's how they can help you master algebra:

1. Instant Solutions

Algebra calculators offer quick and accurate solutions to algebraic problems. Whether you're dealing with equations, inequalities, or complex algebraic expressions, these tools provide instant results, helping you check your work or find solutions more efficiently.

2. Step-by-Step Guidance

Many algebra calculators offer step-by-step solutions. They break down the problem-solving process, helping you understand how to reach the final answer. This feature is invaluable for enhancing your grasp of algebraic concepts.

3. Varied Functions

The best algebra calculators offer a wide range of functions, from solving linear equations to graphing functions. You can explore different algebraic concepts and tackle various problem types with a single tool.

4. Error Minimization

Algebra calculators significantly reduce the chances of calculation errors. By automating the process, they ensure accurate results, allowing you to focus on the conceptual aspects of algebra.

5. Learning Support

While algebra calculators provide quick solutions, they can also serve as learning aids. Many come with tutorials, explanations, and examples to help you build a deeper understanding of algebraic concepts.

Choosing the Best Algebra Calculator

When it comes to mastering algebra, choosing the right algebra calculator is crucial. Look for one that aligns with your specific needs, provides clear and user-friendly instructions, and offers a comprehensive set of algebraic functions. Additionally, ensure that it provides an intuitive interface and excellent customer support for any questions or concerns.

In Conclusion

Mastering algebra is not only essential for academic success but also a valuable skill for real-life problem-solving. The best algebra calculator can be your trusted companion in this journey, simplifying complex problems, enhancing your understanding of algebraic concepts, and ultimately helping you gain the confidence needed to excel in algebra and beyond. So, whether you're a student looking to improve your math skills or a professional seeking to apply algebraic principles, consider adding the best algebra calculator to your toolkit.

#myassignmenthelp #Algebra Calculator

0 notes

positivelyprime · 5 months ago

Text

~~ Erat ~~

What's more fun than ordinary differential equations? That's right, partial differential equations! Although this was really the course I enjoyed the least over the last semester, but whatever. There were two parts to the course: One on general undergraduate-level theory (not a prereq) and one on elliptic theory and Sobolev spaces. Closed book, 3 smaller questions for each part.

Q1: Had us consider a PDE connected to a Sturm-Liouville type ODE via separation of variables, and had us solve said PDE (rare) via a L2 coefficients expansion. Not too exciting and not why I did the course, any physicist could do this (albeit less rigorously) 6/10.

Q2: For the so-called Linear Swift-Hohenberg equation, derive a solution formula for solutions using the Fourier transform. Use this to find some constants so that the solution with u_0 is some cosine exploded as time goes to infinity. Honestly I really like using the Fourier transform to find qualitative results of solutions, but unfortunately this one had us calculate the Fourier transform of the cosine, which you need distribution theory for to do rigorously (dirac deltas), which was not at all covered in the course... Otherwise cool question 7/10 could have been an 8.

Q3: State Hille-Yosida theorem and show the solution from last exercise is a semigroup. Nothing special, but free points and makes sense they ask this 7/10.

Q4: For a given elliptic PDE, show that for C^2 solutions a certain integral property holds, and define a weak solution accordingly. Then show there always exists a weak solution in H^1 (using Lax-Milgram). A classic question, basically the point of the course for me. Quite a lot of calculating and passing through limits, but rewarding in the end 8.5/10.

Q5: Show a certain function has a weak derivative and show some inequality for smooth functions, which you can extend to W^1,p functions. For this I just straight up goofed. Was supposed to be an easy question but CLEARLY positives and negatives don't cancel out, so I screwed everything up. Decent question otherwise though 7/10.

Q6: Show some bound on the H2 norm of a solution to `elliptic operator u = f` compared to the L2 norm of u and f. Honestly just barely had time for this question so I quickly scrabbled somethings that some terms would cancel. Also had a subequestion to state Fredholm's alternative which I did cause that is easier, just remembering. Maybe a cool question? Idk really 6.5/10.

Overall, a fine exam but nothing which really blew my mind. To be honest this was the course I was least hyped about anyways, so in the end that only makes sense. Was representative though so also a solid 7.

About to take three math exams in a three day period. I studied well enough I think but still going to be a challenge. As such, I will rate every question on a scale of 1-10 after the exam, but not based on their difficulty but rather on their interestingness

#mathblr #exam stress

27 notes · View notes

upboardblog-blog · 6 years ago

Link

#solving linear inequations in one variable #Icsesolutionsclass10mathematics

4 notes · View notes

backkilop · 3 years ago

Text

Quadratic inequalities

#QUADRATIC INEQUALITIES HOW TO#

#QUADRATIC INEQUALITIES FULL#

We hope you found this Math math tutorial "Quadratic Inequalities" useful.

Continuing learning inequalities - read our next math tutorial: Graphing Inequalities.

See the Inequalities Calculators by iCalculator™ below.

#QUADRATIC INEQUALITIES FULL#

Check your calculations for Inequalities questions with our excellent Inequalities calculators which contain full equations and calculations clearly displayed line by line.Test and improve your knowledge of Quadratic Inequalities with example questins and answers Inequalities Practice Questions: Quadratic Inequalities.Print the notes so you can revise the key points covered in the math tutorial for Quadratic Inequalities Inequalities Revision Notes: Quadratic Inequalities.Helps other - Leave a rating for this tutorial (see below) Solving Quadratic Inequalities by Studying the SignĮnjoy the "Quadratic Inequalities" math tutorial? People who liked the "Quadratic Inequalities" tutorial found the following resources useful: Inequalities Learning Material Tutorial ID Please select a specific "Quadratic Inequalities" lesson from the table below, review the video tutorial, print the revision notes or use the practice question to improve your knowledge of this math topic. Therefore, we are dedicating this entire tutorial only to quadratic inequalities. Obviously, such inequalities are more complicated to solve compared to linear ones. inequalities that contain one of the variables in the second power.

#QUADRATIC INEQUALITIES HOW TO#

Now, we will explain how to solve quadratic inequalities, i.e. In the previous tutorial, we explained how to solve linear inequalities in one or two variables. How to find the solution set(s) of a quadratic inequality?.How to study the sign of a quadratic inequality?.What happens to the sign of a quadratic inequality when the discriminant is positive? Zero? Negative?.How to write a quadratic inequality in the standard form?.How to identify whether a given number is a root of a quadratic inequality or not?.We also know the endpoints are excluded since 3 creates a denominator of zero and we have a strict inequality.Inequalities Learning Material Tutorial ID $$(-2)^2 - 5(-2) - 6 > 0$$ $$4 + 10 - 6 > 0$$ $$ equire$$ Since the test of the number 4 produces a false statement, we know values that are greater than 4 will not satisfy the inequality. Let's choose -2, we will plug this in for x in the original inequality. Let's begin with interval A, we can choose any value that is less than -1. Step 3) Substitute a test number from each interval into the original inequality. This interval is labeled with the letter "C". Lastly, we have an interval that consists of any number that is greater than 6. This interval is labeled with the letter "B". One interval contains any number less than -1 and is labeled with the letter "A". On the horizontal number line, we can set up three intervals: We have split the number line up into three intervals. These endpoints will allow us to set up intervals on the number line. $$x^2 - 5x - 6 > 0$$ Step 1) We will change this inequality into an equality and solve for x. The endpoints are included for a non-strict inequality and excluded for a strict inequalityĮxample 1: Solve each inequality.If a test number makes the inequality false, the region that includes that test number is not in the solution set.If the test number makes the inequality true, the region that includes that test number is in the solution set.Substitute a test number from each interval into the original inequality.Use the endpoints to set up intervals on the number line.These endpoints separate the solution regions from the non-solution regions.The solutions will give us the boundary points or endpoints.Replace the inequality symbol with an equality symbol and solve the equation.Quadratic Inequalities A quadratic inequality is of the form: $$ax^2 + bx + c > 0$$ Where a ≠ 0, and our ">" can be replaced with any inequality symbol. In this lesson, we will learn how to solve quadratic and rational inequalities.

#Quadratic inequalities

0 notes

kerlonultra · 3 years ago

Text

Factoring expressions

If the sign of the last term is positive, (1) find two numbers (both will be positive or both will be negative) whose product is the last term and whose sum is the coefficient of the middle term and (2) give both factors the sign of the middle term.įirst check to see whether you can monomial factor (factor out common terms). If the sign of the last term is negative, (1) find two numbers (one will be a positive number and the other a negative number) whose product is the last term and whose difference is the coefficient (number in front) of the middle term and (2) give the larger of these two numbers the sign of the middle term and the opposite sign to the other factor. To decide on the signs of the numbers, do the following. (2) Factor the last term and place the factors in the right sides of the parentheses. Place these factors in the left sides of the parentheses. Then if a = 1 (that is, the first term is simply x 2), use double parentheses and factor the first term. To factor polynomials having three terms of the form ax 2 + bx + c, (1) check to see whether you can monomial factor (factor out common terms). To factor the difference between two squares, (1) find the square root of the first term and the square root of the second term and (2) express your answer as the product of the sum of the quantities from Step 1 times the difference of those quantities.įactoring polynomials having three terms of the form ax 2 + bx + c When the common monomial factor is the last term, 1 is used as a place holder in the second factor.įactoring the difference between two squares To factor out a common factor, (1) find the largest common monomial factor of each term and (2) divide the original polynomial by this factor to obtain the second factor. To factor means to find two or more quantities whose product equals the original quantity. Quiz: Linear Inequalities and Half-Planes.Solving Equations Containing Absolute Value.Inequalities Graphing and Absolute Value.Quiz: Operations with Algebraic Fractions.Solving Systems of Equations (Simultaneous Equations).Quiz: Solving Systems of Equations (Simultaneous Equations).Quiz: Variables and Algebraic Expressions.Signed Numbers (Positive Numbers and Negative Numbers).Quiz: Simplifying Fractions and Complex Fractions.Simplifying Fractions and Complex Fractions.Quiz: Signed Numbers (Positive Numbers and Negative Numbers).Quiz: Multiplying and Dividing Using Zero.Quiz: Properties of Basic Mathematical Operations.Properties of Basic Mathematical Operations.

#Factoring expressions

0 notes

mademains · 3 years ago

Text

Quadratic inequalities

#QUADRATIC INEQUALITIES HOW TO#

To be neat, the smaller number should be on the left, and the larger on the right. The distance we want is from 10 m to 15 m: (Note: if you are curious about the formula, it is simplified from d = d 0 + v 0t + ½a 0t 2, where d 0=20 , We can use this formula for distance and time: We also know the endpoints are excluded since 3 creates a denominator of zero and we have a strict inequality.A stuntman will jump off a 20 m building.Ī high-speed camera is ready to film him between 15 m and 10 m above the ground. $$(-2)^2 - 5(-2) - 6 > 0$$ $$4 + 10 - 6 > 0$$ $$ equire$$ Since the test of the number 4 produces a false statement, we know values that are greater than 4 will not satisfy the inequality. Let's choose -2, we will plug this in for x in the original inequality. We can solve quadratic inequalities to give a range of. Let's begin with interval A, we can choose any value that is less than -1. Quadratic inequalities are similar to quadratic equations and when plotted they display a parabola. Step 3) Substitute a test number from each interval into the original inequality. This interval is labeled with the letter "C". The solution to a quadratic inequality in one variable can have no values, one value or. Let us consider the quadratic inequality x2 5x Lastly, we have an interval that consists of any number that is greater than 6. The standard quadratic equation becomes an inequality if it is represented as ax2 + bx + c 0).

This interval is labeled with the letter "B". One interval contains any number less than -1 and is labeled with the letter "A". Quadratic Inequalities Given 3 x 2 > -x + 4 Rewrite the inequality with one side equal to zero. On the horizontal number line, we can set up three intervals: We have split the number line up into three intervals. It shows the data which is not equal in graph form. Introduces a conceptual basis for solving quadratic inequalities, looking at linear inequalities and using a knowledge of what quadratic graphs look like. An equation is a statement that asserts the equality of two expressions and a linear inequality is an inequality which involves a linear function. These endpoints will allow us to set up intervals on the number line. In quadratic inequalities worksheets, we learn that a quadratic inequality is an equation of second degree that uses an inequality sign instead of an equal sign. Therefore, set the function equal to zero and solve. For a quadratic inequality in standard form, the critical numbers are the roots. $$x^2 - 5x - 6 > 0$$ Step 1) We will change this inequality into an equality and solve for x. It is important to note that this quadratic inequality is in standard form, with zero on one side of the inequality.

The endpoints are included for a non-strict inequality and excluded for a strict inequalityĮxample 1: Solve each inequality.

If a test number makes the inequality false, the region that includes that test number is not in the solution set.

If the test number makes the inequality true, the region that includes that test number is in the solution set.

If it is less than or greater than some number or any other polynomial. Consider a quadratic polynomial ax2+bx+c.

Substitute a test number from each interval into the original inequality Graphing a quadratic inequality is easier than you might think You just need to know the steps involved This tutorial takes you through those steps to. What do you mean by Quadratic inequalities.

For example, to solve a quadratic inequality -x2+x+2>0, we can find the values of x where the parabola.

Use the endpoints to set up intervals on the number line Students will solve quadratic inequalities and match each inequality with its solution set. Quadratic inequalities are best visualized in the plane.

These endpoints separate the solution regions from the non-solution regions.

If the quadratic inequality is not in one of the. is an example of a quadratic inequality, as it contains a single variable raised to the second power at maximum.

The solutions will give us the boundary points or endpoints Hence, we obtain four possible general forms of quadratic inequalities: ax 2 + bx + c > 0.

Replace the inequality symbol with an equality symbol and solve the equation.

Quadratic Inequalities A quadratic inequality is of the form: $$ax^2 + bx + c > 0$$ Where a ≠ 0, and our ">" can be replaced with any inequality symbol.

#QUADRATIC INEQUALITIES HOW TO#

In this lesson, we will learn how to solve quadratic and rational inequalities.

#Quadratic inequalities

0 notes

yesinstantfacecollectionlov-blog · 7 years ago

Text

Test Bank for Beginning and Intermediate Algebra 5th Edition by Elayn Martin Gay

link full download: https://nursingtestbankdownload.com/product/test-bank-for-beginning-and-intermediate-algebra-5th-edition-by-elayn-martin-gay/

This is completed downloadable Test Bank for Beginning and Intermediate Algebra 5th Edition by Elayn Martin Gay

Instant download Test Bank for Beginning and Intermediate Algebra 5th Edition by Elayn Martin Gay after payment

Click the link below to view the chapter of test bank:

https://nursingtestbankdownload.com/wp-content/uploads/2018/03/Test-Bank-for-Beginning-and-Intermediate-Algebra-5th-Edition-by-Elayn-Martin-Gay.pdf

Test Bank for Beginning and Intermediate Algebra 5th Edition by Elayn Martin Gay

Elayn Martin-Gay’s developmental math textbooks and video resources are motivated by her firm belief that every student can succeed. Martin-Gay’s focus on the student shapes her clear, accessible writing, inspires her constant pedagogical innovations, and contributes to the popularity and effectiveness of her video resources (available separately). This revision of Martin-Gay’s algebra series continues her focus on students and what they need to be successful.

Table of Contents

1. Review of Real Numbers 1.1 Tips for Success in Mathematics 1.2 Symbols and Sets of Numbers 1.3 Fractions and Mixed Numbers 1.4 Exponents, Order of Operations, Variable Expressions and Equations 1.5 Adding Real Numbers 1.6 Subtracting Real Numbers Integrated Review–Operations on Real Numbers 1.7 Multiplying and Dividing Real Numbers 1.8 Properties of Real Numbers 2. Equations, Inequalities, and Problem Solving 2.1 Simplifying Algebraic Expressions 2.2 The Addition and Multiplication Properties of Equality 2.3 Solving Linear Equations Integrated Review–Solving Linear Equations 2.4 An Introduction to Problem Solving 2.5 Formulas and Problem Solving 2.6 Percent and Mixture Problem Solving 2.7 Further Problem Solving 2.8 Solving Linear Inequalities 3. Graphing 3.1 Reading Graphs and the Rectangular Coordinate System 3.2 Graphing Linear Equations 3.3 Intercepts 3.4 Slope and Rate of Change Integrated Review–Summary on Slope and Graphing Linear Equations 3.5 Equation of Lines 3.6 Functions 4. Solving Systems of Linear Equations 4.1 Solving Systems of Linear Equations by Graphing 4.2 Solving Systems of Linear Equations by Substitution 4.3 Solving Systems of Linear Equations by Addition Integrated Review–Solving Systems of Equations 4.4 Solving Systems of Linear Equations in Three Variables 4.5 Systems of Linear Equations and Problem Solving 5. Exponents and Polynomials 5.1 Exponents 5.2 Polynomial Functions and Adding and Subtracting Polynomials 5.3 Multiplying Polynomials 5.4 Special Products Integrated Review–Exponents and Operations on Polynomials 5.5 Negative Exponents and Scientific Notation 5.6 Dividing Polynomials 5.7 Synthetic Division and the Remainder Theorem 6. Factoring Polynomials 6.1 The Greatest Common Factor and Factoring by Grouping 6.2 Factoring Trinomials of the Form x2 + bx + c 6.3 Factoring Trinomials of the Form ax2 + bx + c by Perfect Square Trinomials 6.4 Factoring Trinomials of the Form ax2 + bx + c by Grouping 6.5 Factoring Binomials Integrated Review–Choosing a Factoring Strategy 6.6 Solving Quadratic Equations by Factoring 6.7 Quadratic Equations and Problem Solving 7. Rational Expressions 7.1 Rational Functions and Simplifying Rational Expressions 7.2 Multiplying and Dividing Rational Expressions 7.3 Adding and Subtracting Rational Expressions with Common Denominators and Least Common Denominator 7.4 Adding and Subtracting Rational Expressions with Unlike Denominators 7.5 Solving Equations Containing Rational Expressions Integrated Review–Summary on Rational Expressions 7.6 Proportion and Problem Solving with Rational Equations 7.7 Simplifying Complex Fractions 8. More on Functions and Graphs 8.1 Graphing and Writing Linear Functions 8.2 Reviewing Function Notation and Graphing Nonlinear Functions Integrated Review–Summary on Functions and Equations of Lines 8.3 Graphing Piecewise-Defined Functions and Shifting and Reflecting Graphs of Functions 8.4 Variation and Problem Solving 9. Inequalities and Absolute Value 9.1 Compound Inequalities 9.2 Absolute Value Equations 9.3 Absolute Value Inequalities Integrated Review–Solving Compound Inequalities and Absolute Value Equations and Inequalities 9.4 Graphing Linear Inequalities in Two Variables and Systems of Linear Inequalities 10. Rational Exponents, Radicals, and Complex Numbers 10.1 Radicals and Radical Functions 10.2 Rational Exponents 10.3 Simplifying Radical Expressions 10.4 Adding, Subtracting, and Multiplying Radical Expressions 10.5 Rationalizing Denominators and Numerators of Radical Expressions Integrated Review–Radicals and Rational Exponents 10.6 Radical Equations and Problem Solving 10.7 Complex Numbers 11. Quadratic Equations and Functions 11.1 Solving Quadratic Equations by Completing the Square 11.2 Solving Quadratic Equations by the Quadratic Formula 11.3 Solving Equations by Using Quadratic Methods Integrated Review–Summary on Solving Quadratic Equations 11.4 Nonlinear Inequalities in One Variable 11.5 Quadratic Functions and Their Graphs 11.6 Further Graphing of Quadratic Functions 12. Exponential and Logarithmic Functions 12.1 The Algebra of Functions; Composite Functions 12.2 Inverse Functions 12.3 Exponential Functions 12.4 Exponential Growth and Decay Functions 12.5 Logarithmic Functions 12.6 Properties of Logarithms Integrated Review–Functions and Properties of Logarithms 12.7 Common Logarithms, Natural Logarithms, and Change of Base 12.8 Exponential and Logarithmic Equations and Problem Solving 13. Conic Sections 13.1 The Parabola and the Circle 13.2 The Ellipse and the Hyperbola Integrated Review–Graphing Conic Sections 13.3 Solving Nonlinear Systems of Equations 13.4 Nonlinear Inequalities and Systems of Inequalities 14. Sequences, Series, and the Binomial Theorem 14.1 Sequences 14.2 Arithmetic and Geometric Sequences 14.3 Series Integrated Review–Sequences and Series 14.4 Partial Sums of Arithmetic and Geometric Sequences 14.5 The Binomial Theorem Appendix A. Operations on Decimals/Percent, Decimal, and Fraction Table Appendix B. Review of Algebra Topics Appendix C. An Introduction to Using a Graphic Utility Appendix D. Solving Systems of Equations by Matrices Appendix E. Solving Systems of Equations by Determinants Appendix F. Mean, Median, and Mode Appendix G. Review of Angles, Lines, and Special Triangles

Product DetailsISBN-13: 978-0321785121ISBN-10: 1256776181

2 notes · View notes

onlineacademicclasses · 4 years ago

Link

ALGEBRA HOMEWORK HELP

Begin improving grades in Algebra with every minute of 24/7 schoolwork help from the algebra coach. Our mentors are specialists in Algebra I and are prepared to assist you with your particular Algebra issue.

All Algebra Skill Levels and Concepts

Discover an Algebra mentor online whenever you're working at schoolwork or examining—after training, before class, or at the ends of the week. We help algebra understudies in all grades and expertise levels—

including Pre-Algebra, Algebra I, and Algebra II—find support with Algebra ideas, including Linear inequalities, Graphing equations

• Algebraic expressions

• Algebraicequations

• Algebra word problems

• Algebra formulas

• Factoring polynomials

Our Algebra coaches can assist you to do Algebra homework, quizzes, exams, tests and assignments.

Coordinated Algebra Help

You'll get customized, balanced assistance from our master coaches. Inform us regarding your concern, and we'll track down the best mentor for you. Both tutor and the student will attend our online class and try to solve Algebra questions, check Algebra schoolwork, and survey Algebra formulas.

Polynomial math Tutoring That Gets Results

Students who use algebra homework helpers improve grades, feel more certain and complete their schoolwork on schedule. Begin improving grades in your algebra class—discover an Algebra guide now.

Algebra Homework Help

-The Solution To All Your Problems As referenced before, the specialists of our assistance in my variable-based math schoolwork administration know the particular issues that understudies face. We include the right answers for each of your problems in algebra class. You can totally depend on us for taking care of issues of algebra essays.

Here is a portion of the issues that understudies face and on the off chance that you feel to be in a similar circumstance, visit us: Absence of a solid Mathematical establishment - It is fundamental for everybody to have essential arithmetic information and knowledge of number hypothesis ideas. Without this, the shot at making blunders in the task remains. With our Algebra Homework help, you will clear all your queries in algebra.

Hence, you will not face any problems on facing Algebra. Unfit to comprehend the theoretical idea of Algebra - Algebra is definitely more not the same as some other part of maths. In algebra, understudies need to discover the potential responses for an arithmetical articulation that has been given to them. You may find problems in solving algebra problems. with our master's assistance, you'll have the choice to get your work done. Unable to understand basic equations - If you need to take care of polynomial math issues, you should realize how to settle essential conditions. Do you think that it's hard to tackle fundamental conditions? Then, at that point, an Algebra homework help is the place where you should be. In this manner, with our schoolwork help for algebra 1 and different courses, every one of your issues will be no more. Regardless issue you are battling with, the specialists in our group can likewise give Algebra homework help to every significant issue.

https://www.domyonlinealgebraclass.com/

#online math classes

0 notes

mooptcom · 4 years ago

Text

Boring Notes of Linear Programming

Linear Programming is a mathematical technique to find the optimal value for a linear system of objective function and constraints.

Modeling is an art, not a precise science. All mathematical models necessarily contain some degree of simplification of the real world that we are attempting to describe.

Different modelers will make different assumptions, and come up with different models of more or less precision, and certainly of different sizes, having different numbers of decision variables.

Linear Programming (LP)

Linear programming (LP) is the best known mathematical optimization technique to allocate scarce resources to competing activities in an optimal manner when the problem can be expressed with continuous decision variables, linear in both objective function and inequality constraints.

LP is the first category of optimization problems that were considered by early scientists and researchers in the OR field.

It turns out that many models can be cast in the form of LP models, without too many wild assumptions.

To solve an optimization problem, a model file contains at least the elements, i.e Objective Function, Constraints and Bounds.

1) Objective Functions

Objective function is a mathematical representation of the business objectives or goals to be achieved. It always starts with maximize or minimize of the outputs, for minimizing costs or maximizing revenue.

$\min c_1 x_1 + c_2 x_2 +\ ...\ +\ c_n x_n$

min means minimize. It can be maximize based on modeler's logic.

$c_1, c_2, ..., c_n$ are the objective function coefficients.

$x_1, x_2, ..., x_n$ are the variables or unknowns.

2) Constraints

Constraints are the elements that limit or restrict the decision variables in some way.

$\begin{aligned} a_{11} x_1 + a_{12} x_2 + ... + a_{1n} x_n \leq b_1 \\\ a_{21} x_1 + a_{22} x_2 + ... + a_{2n} x_n \leq b_2 \\\ ... \\\ a_{m1} x_1 + a_{m2} x_2 + ... + a_{mn} x_n \leq b_m \\\ x1, x2, ..., x_n \geq 0 \end{aligned}$

$a_{11}, a_{12}, ..., a_{1n}, a_{m1}, a_{m2}, ..., a_{mn}$ are the constraint coefficients.

$\leq, \geq, \lt, \gt$ are the relations between both sides in inequalities form.

$b_1, b_2, ..., b_m$ are the righthand side values.

3) Bounds

Bounds are the special contraints to define lower and upper boundaries.

$l_1 \leq x_1 \leq u1,\ ...,\ l_n \leq x_n \leq u_n$

$u_1, u_2, ..., u_n$ are the upper bounds.

$l_1, l_2, ..., l_n$ are the lower bounds.

This is the Simplest Structure of a Model with the conventional form or typical symbolic representation of a LP.

Minimize (or Maximize) c1 x1 + c2 x2 + ... + cn xn Subject To a11 x1 + a12 x2 + ... + a1n xn = 0 l1 = 0

model starts with the objective, i.e. to minimize a linear function.

c is the vector of objective coefficients.

s.t. means subject to constraints in the form of linear expressions.

b is the vector of right-hand side constants of constraints.

A is the matrix of constraint coefficient.

x is the decision variable.

$x \geq 0$ is the variable domain.

This example shows how to a general linear programming problem, and illustrates how scripting can be combined with the model to display results and obtain details on the solution. The problem we want to solve can be written in matrix form as

$\begin{aligned} \max c^T x \\\ s.t.\ A_x \leq b \\\ x \geq 0 \\\ \end{aligned}$

Simplest form of a LP

min c^T x s. t. Ax = b x >= 0

$c^T$ is the c transpose x.

if y represents the dual variables for a given basic solution, the reduced costs are defined as $c - y^T A$.

the basic solution is optimal if $c - y^T A \geq 0$.

if all reduced costs for this LP are non-negative, it follows that the objective value can only increase with a change in variable value and therefore the solution when minimizing is optimal.

for large LPs, the reduced costs can be used to determine whether multiple optimal solutions exist.

Multiple solutions exist when at least one non-basic variable with a zero reduced cost exists in an optimal solution, that is, the variables values that can change without affecting the objective values.

It is possible that a LP has multiple optimal solutions. This can happen when the slope of the objective function is the same as the slope of the constraints.

We have stressed the linearity condition, where the objective function and all of the constraints must be linear in the decision variables. But there are two further properties that we must have, which are Divisibility and Determinism.

Divisibility means that in an acceptable solution any values of the decision variables are allowed within the restrictions imposed by the linear constraints. In particular, we are not constrained to accept only whole number (integer) values for some or all of the decision variables.

Deterministic requires all the coefficients in the constraints and the objective function are known exactly. Determinism is sometimes a very strong assumption, particularly if we are building planning models which extend some way into the future.

Problems where we must consider the Variability in objective function coefficients, right hand sides or coefficients in the constraints are Stochastic Programming problems. In fact, it can be argued that all planning models have stochastic elements and we will later demonstrate some methods for dealing with uncertainty in an LP framework.

Nowadays Linear Programming is still frequently taught from a very academic perspective. With the exception of a few students in applied mathematics who have learned to deal with applications, the others do not retain much.

In the coming lessons, we will show you the possible applications, readily available software tools and most importantly, the best practice on how to model.

#note #lp #linear programming #linear optimization #Mathematical programming #school

1 note · View note

mathematicianadda · 5 years ago

Text

Coding Stories: Programming Polygons https://ift.tt/3eyZ6FV

In this guest post, Greg Benedis-Grab shares the story of when he discovered Pick’s Theorem, and how he coded an interactive version to play with.

Have you ever been intoxicated by a mathematical theorem? Well that’s what happened to a class of 9th grade geometry students at my school. Their enthusiastic teacher showed them Pick’s theorem.

“What is Pick’s Theorem?” I asked after she described the reaction of her students. So she showed me an example:

https://en.wikipedia.org/wiki/Pick%27s_theorem

Using a lattice of nails and a rubber band, you can create geometric shapes where each vertex is located on a lattice point. As she was telling me about it I remembered this fun math manipulative from my own Elementary school days. The theorem requires you to categorize some of the lattice points as boundary points, b and interior points, i. The expression for the area is given below.

\[\textcolor{red}{i=7} \qquad \textcolor{green}{b=8}\]

\[A = \textcolor{red}{i} + \frac{\textcolor{green}{b}}{2}\ – 1 = 10\]

That is a pretty surprising result – at least, that is what the 9th grade students thought. I will leave the proof of this to the mathematicians. Here is a link to a particularly engaging mathematician doing just that. I am more interested in displaying colorful shapes in the browser so I decided it would make for a nice p5.js sketch. To get this project started I needed a very simple case. Say you have a 10×10 grid and the simplest of polygons, the triangle.

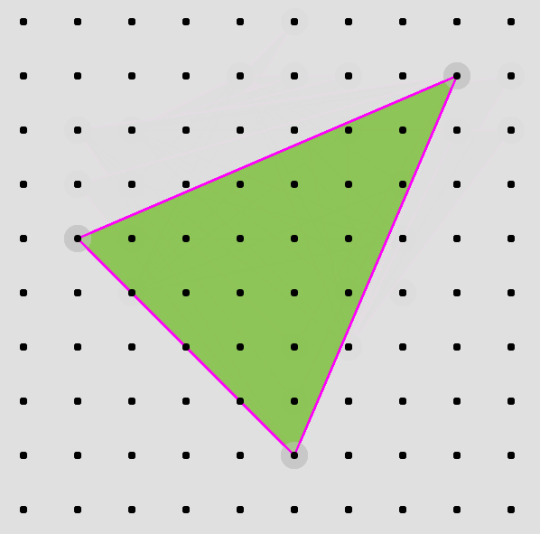
A triangle is defined by its three vertices. To organize my code I will create a Vetex class to store the x,y values for each vertex in the triangle.

class Vertex { constructor(x, y) { this.x = x; this.y = y; } show(spacing) { fill(200); // light grey circle around each vertex circle(this.x*spacing, this.y*spacing,30); } }

The spacing variable allows me to space out the grid points according to the window size. Next I decided to draw all the grid points on the screen.

function drawBoard(spacing) { stroke(0); strokeWeight(8); for (let i=0;i<10;i++) { for (let j=0;j<10;j++) { point(i*spacing,j*spacing); } } }

Finally, I need to draw and fill in the triangle. I included this code in the draw loop to do so.

fill(135,180,70,100); // green strokeWeight(2); stroke(255,0,255); // violet beginShape(); vertices.forEach((v)=>vertex(v.x*spacing, v.y*spacing)); let v = vertices[0]; vertex(v.x*spacing, v.y*spacing); endShape();

I also added the ability to drag vertices to new positions. To do this I included the following methods to the Vertex class

mousePressed(mouse) { let pos = createVector(this.x*spacing, this.y*spacing); pos.add(offset); // offset allows the lattice to be centered if (pos.dist(mouse) < 30) { this.dragging = true; // assigns Vertex attribute } } update() { if (this.dragging) { let x = int(mouseX/spacing -0.5); let y = int(mouseY/spacing - 0.5)-1; if (x>=0 && x<10 && y>=0 && y<10) { this.x = x; this.y = y; } } }

The dragging attribute indicates that one of the vertices is being dragged and should update its position with the mouse. The fact that the vertices are objects means that each of the vertex objects has its own dragging attribute and can be independently dragged. Objects will also allow me later to scale up this project to have an arbitrary number of vertices in my shape. Finally, I had to add the following functions to sketch.js in order to handle the click events. The first defines a predefined mousePressed() function that subsequently passed the mouse position to an identically named method in the Vertex class. That method checks if the mouse event occurred on the given vertex. The second removes the dragging attribute from all vertices when the mouse is released.

function mousePressed() { let mouse = createVector(mouseX,mouseY); // makes new triangle when title is clicked if (mouseY<0) makeTriangle(); vertices.forEach((v)=>v.mousePressed(mouse)); }function mouseReleased() { for (let v of vertices) if (v.dragging) delete v.dragging; }

Finally I made sure the update() and show() methods are run for each vertex object.

vertices.forEach((v)=>{ v.show(); v.update(); });

And that creates the following exciting web app. Go ahead and make some triangles.

Of course at this point all I have created is a triangle generator. We have not yet explored Pick’s Theorem. To do that I need to determine which lattice points are on the boundary and which points are interior. Before moving to this important step I cleaned up the code. It is important to take time to clean up your code as you expand it. Otherwise it can become unwieldy and impossible to debug. Well organized code can make complex problems simple and elegant to solve. The simplicity of the code often hides the hard work that goes into simplifying it and finding the right organization. The organization scheme serves as a foundation upon which new functionality can be built. I added a Triangle class and a Board class to modularize the program making my methods and attributes easy to manipulate.

class Triangle { constructor() { this.vertices = []; while(this.vertices.length<3) { const x = int(random(board.w)); const y = int(random(board.h)); const v = new Vertex(x,y); // only add the point if it is not on another one. if (!this.isVertex(x,y)) this.vertices.push(v); } } isVertex(i,j) { for (let v of this.vertices) { if (i == v.i && j == v.j) return true; } return false; } update() { this.vertices.forEach((v)=>v.update()); } show() { // draw the triangle as shown previously } }class Board { constructor() {} // set up board and creates a triangle obj. showLattice() {} // draws the lattice points update() { this.triangle.update(); } menu() {} // group all the menu info together show() { this.triangle.show(); this.showLattice(); this.menu(); } }

Next I spent a fair amount of time thinking about how to mathematically define the boundary and the interior of the shape. I needed a good algorithm to accomplish this task. This is where the story gets interesting.

Computers can solve challenging mathematical problems. They perform calculations at astonishing speeds. The tricky part of this problem is that I am not sure what calculation needs to be performed. If I have a point (x,y) how will I know if it is on the boundary of my shape, inside of my shape or neither of these two conditions. To be honest I first stared at the problem for a long time. Then I noticed that the triangle has three line segments associated with it that can be drawn between pairs of vertices. These three lines can be expressed as linear equations. For points in the lattice that are located on one of the three line segments they are by definition boundary points. Checking the slope and that the points coordinates lie between the segment endpoint coordinates should be sufficient. Here is how I wrote the code.

colinear(i,j,a,b) {return (j-a.j)*(b.i-a.i) == (b.j-a.j)*(i-a.i);} inbounds(i,j,a,b) { return i >= min([a.i,b.i]) && i <= max([a.i,b.i]) && j >= min([a.j,b.j]) && j <= max([a.j,b.j]); }isBoundary(x,y) { let v0 = this.vertices[0]; let v1 = this.vertices[1]; let v2 = this.vertices[2]; // checks if it is on any of the 3 line segments return (this.colinear(x,y,v0,v1) && this.inbounds(x,y,v0,v1) || this.colinear(x,y,v1,v2) && this.inbounds(x,y,v1,v2) || this.colinear(x,y,v2,v0) && this.inbounds(x,y,v2,v0)) }

For the interior points I can simply check that the given lattice point satisfies the inequality for the three line segments that make up the triangle. Then I wondered, how do I know which side of the inequality is correct. The third point of the triangle, the point that is not part of the given edge should match the correct inequality for the given point. In other words if the lattice point is on the same side of the line as the third point then it satisfies that edge’s inequality. Now I just need to test all three edges and I can define the interior lattice points for the triangle. Here is how I coded this in the Triangle class.

inEq(x,y) {return (j-a.j)*(b.i-a.i) < (b.j-a.j)*(i-a.i);} isInterior(x,y) { let v0 = this.vertices[0]; let v1 = this.vertices[1]; let v2 = this.vertices[2]; //check that the point has the same inequality outcome as the 3rd //point for each of the line segments. return (this.inEq(x,y,v0,v1) == this.inEq(v2.x,v2.y,v0,v1) && this.inEq(x,y,v1,v2) == this.inEq(v0.x,v0.y,v1,v2) && this.inEq(x,y,v2,v0) == this.inEq(v1.x,v1.y,v2,v0))

Now my app can show the number of green interior points and pink boundary points and count them on the top of the screen. I also added some animation movement to the triangle and a slider to control the speed of the animation.

This is a fun way to explore Pick’s Theorem. A teacher might use it to have students explore various triangles and see if they can come up with the theorem themselves. They can also look for patterns in the two output values to gain more insight into triangles. So one way that p5 can transform student mathematical thinking is to create a catalogue of engaging sketches such as these. Even better mathematics teachers can make their own sketches to target learning based on their knowledge about the students in their classes. For me the real learning happened when I tried to write the sketch myself. Getting the program to work deepened my level of geometric understanding and gave me an appreciation for Pick’s theorem.

Unfortunately, it is difficult to incorporate this kind of work in our high school math courses because of how much time it consumes. In addition to figuring out the mathematics I had to spend a fair amount of time debugging my code making sure that my calculations were working as expected. A number of times I had to debug the code and think systematically through the program to find my own error. The debugging process was equal in intellectual rigor to the rules I created for the inequalities. Especially since many math teachers and students are not as comfortable with coding as I am this aspect of the process could dominate and stifle the math learning. However despite these challenges I think it is still worth thinking about how we can use problems like this in math class to deepen student thinking and make the process of mathematics more playful and interactive.

The teacher who introduced this problem to me was nice enough to invite me in to her class to share my web app. I first talked to them a little about p5 and how you make shapes on the screen. Then I explained the dilemma with defining the boundary points and the interior points. I challenged them to develop their own algorithmic steps to make this determination for each lattice point. They came up with my solution very quickly. I was a bit humbled by how long it had taken me. Once they explained their algorithm I showed them how I coded it using JavaScript. They wanted to extend the idea to polygons with more than three vertices. We quickly realized that for convex polygons the same approach would work. I just had to come up with a way to handle more vertices. So I wrote the following loop to find all the edges of a polygon defined by an array of vertices. Notice that I renamed the attribute .triangle to now be .polygon

vs = board.polygon.vertices; for (let i = 0, j = vs.length - 1; i < vs.length; j = i++) { // each iteration of the loop will identify a unique edge // defined by the points vs[i] and vs[j] }

With this loop I can now check all the edges to see if a lattice point is a boundary point. I can also perform my inequality function on all the edges to see if it is interior (though I also need to pick one of the non-colinear points). Since I used a Vertex class to define the vertices and stored them in an array in the triangle shape it was fairly straightforward to change the name of the class to Polygon and adjust the length of the .vertices attribute in the Polygon object. By using an object oriented approach I was able to quickly scale up my idea to all possible lattice polygons.

However my definition of interior points becomes problematic when one of the vertices is concave. In that case one of the rays that extends from the edge intersects the interior of the shape making it more challenging to use the inequality to define the interior. It is possible that we can work around this using a more complex set of Boolean expressions.

Instead I shared with the class a new way to define the interior of a polygon. Ray casting is an elegant way to determine if a point is inside of a polygon. Draw a ray starting at each lattice point to infinity. If the ray passes through an odd number of edges it is interior. Otherwise it is not. If we simply draw a horizontal ray to the right we can algebraically determine the number of crossings. Here is the code I used to determine if a lattice point is inside the polygon defined by the array board.polygon.vertices

let inside = false; vs = board.polygon.vertices; for (let i = 0, j = vs.length - 1; i < vs.length; j = i++) { let xi = vs[i].i, yi = vs[i].j; let xj = vs[j].i, yj = vs[j].j; let intersect=((yi > y) != (yj > y)) && (x < (xj - xi) * (y - yi) / (yj - yi) + xi); if (intersect) inside = !inside; }

With this new algorithm I created a new app using the p5.js editor.

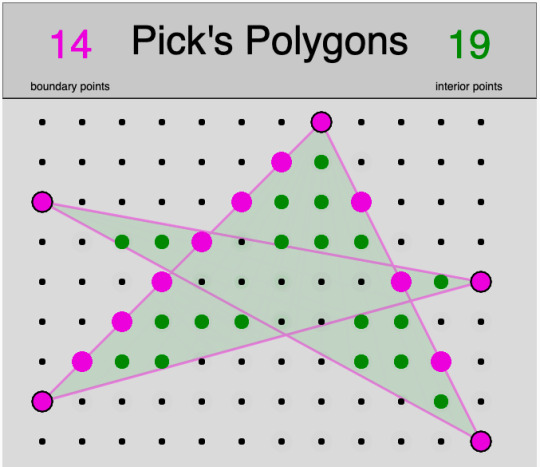
https://editor.p5js.org/gbenedisgrab/sketches/jAIo-Tzev

I let the class play with this new and improved Pick’s Theorem Tool. By the way I added new features so that you can click on a boundary point to make it a vertex. I also made it possible to double click a vertex to remove it. I asked them to explore different shapes and see whether Pick’s theorem always holds and to specifically find when Pick’s theorem does not work. For example if you have a complex polygon (a polygon with edges that intersect) the theorem no longer holds. I then challenged them to find a new expression for complex polygons.

This exploration led to a surprising amount of sophistication. Some students realized that the ray casting rule did not always exactly match the way p5 filled a polygon shape. I might want to explore p5’s algorithm to see how it is defined. Another student noticed that sometimes a ray from an interior point can pass through a vertex and one side of a polygon. This raises an important idea about what it means to pass through an odd number of edges. Additional students worked on coming up with a new algebraic Pick’s expression for complex polygons.

To finish off this article I decided to pursue the intersection between aesthetic beauty and mathematical expression. I decided to create rays that travel across the screen along horizontal paths. Every time the ray passes through a lattice point it will determine how to classify it based on the logic described above – if it lies on the line segment of an edge, it is filled with pink, and if it has passed through an odd number of edges then it is green. Otherwise it is filled with black.

I gave the sketch a radar-like aesthetic, where defined lattice points slowly fade after they are marked. I also lit up the edges as the rays crossed them. Finally I made the polygon randomly transform over time creating a hopefully pleasing dot pattern progression. I will not explain this code in depth, but it is accessible through the glitch sketch linked below.

from The Aperiodical https://ift.tt/3fTHAwj Greg Benedis-Grab from Blogger https://ift.tt/31bh9y2

#Blogger

0 notes

thousandmaths · 8 years ago

Text

Nonvanishing of Littlewood-Richardson Polynomials is in P

This talk was given by Alex Yong at this year’s CA+ conference. He cited Robichaux as a collaborator, as well as high school student Anshul Adve.

------

Factorial Schur Functions

As with all the best combinatorics, we start with a game.

Given a partition (possibly with some zero parts), draw its Young diagram but replace the boxes with black dots and the “positions without boxes” with white dots. Don’t have any extra rows, but extra columns are okay. For instance, the partition $(2,2,0)$ corresponds to this picture

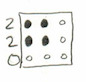
We then make moves according to the following rule, anytime we see a black dot in a TL corner of a square that’s otherwise white, we can move it to the BR corner:

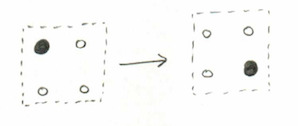
We make this move wherever possible until there are no more available. The set of all diagrams that can be obtained this way, starting with the partition $\lambda$ will be called, uncreatively, $\text{Black}(\lambda)$. To keep with our example, here is $\text{Black}((2,2,0))$:

Now it is time for some algebra: we are going to describe a polynomial in two sets of variables $X=x_1,\dots, x_r$, where $r$ is the number of rows; and $Y=y_1, y_2, y_3,\dots$ representing the columns. First, we define the weight of a diagram $\text{wt}(D)$ to be the product of every $x_i-y_j$, for all $i$ and $j$ such that there is a black dot in row $i$ and column $j$.

Finally, define the factorial Schur function $s_\lambda(X,Y)$ to be the sum of $\text{wt}(D)$ over all diagrams $D\in\text{Black}(\lambda)$. As a formula:

$$ s_\lambda(X,Y) = \sum_{D\in\text{Black}(\lambda)} ~~ \prod_{(i,j)\text{ is black}} x_i-y_j. $$

------

Littlewood-Richardson Polynomials

The reason that factorial Schur functions are called that is because if you plug $y_i=0$ for every $y$, the resulting polynomial is really, honestly, the Schur polynomial. Schur functions form a basis for the symmetric algebra, and so we might hope that the symmetric Schur functions are the basis for something. This hope turns out to be validated: it is a $\Bbb Z[Y]$-module basis of $\Lambda_n\otimes \Bbb Z[Y]$ (The last symbol there is polynomial algebra in the $y$-variables, and the symbol in the middle is a tensor product)

Because of that, this means that $s_\lambda(X,Y)s_\mu(X,Y)$ must be some linear combination, and so we can ask for the structure coefficients $C_{\lambda,\mu}^\nu(Y)$. We write the $Y$ there because in general these things can be an element in $\Bbb Z[Y]$; in other words, can be a polynomial in the $y$-variables.

Since they specialize to the Littlewood-Richardson coefficients when $y_i=0$, we call these $C_{\lambda,\mu}^\nu$ the Littlewood-Richardson Polynomials

[ Because of the geometric interpretation of ordinary Littlewood-Richardson coefficients, we know that they are nonnegative integers; you may ask whether the LR-polynomials are also positive (in that all the coefficients are negative). The answer is no, but they are positive as polynomials in $z_i:=y_{i+1}-y_i$. ]

------

Polynomial Time

In 2005, one day after the other, two papers were posted to the arXiv, both claiming to have proven the following theorem:

Theorem (DeLoera–McAllister 2006, Mulmuley–Narayanan–Sohoni 2012*). There is an algorithm for determining whether or not the Littlewood-Richardson coefficient $c_{\lambda,\mu}^\nu=0$ in polynomial time.

If you’re not super familiar with “polynomial time”, feel free to substitute the word “quickly” anywhere you see it; this isn’t necessarily true but it’s a respectable approximation.

This naturally raises the question of whether the Littlewood-Richardson polynomials can also be determined to be zero or not in polynomial time. As the title of the talk suggests— and as Adve, Robichaux, and Yong proved— the answer is yes. The rest of this section is devoted to a proof sketch.

There is a celebrated proof due to Knutson–Tao which proves the so-called saturation conjecture, that $c_{\lambda,\mu}^\nu=0$ if and only if $c_{N\lambda,N\mu}^{N\nu}=0$ for all $N$. At this point, Yong talked a little bit about the history of that conjecture:

In the 19th century, people were asking this question about Hermetian matrices.

In 1962 Horn conjectured a bunch of inequalities which resolved the question.

In 1994 Klyachko solved the problem, but didn’t use Horn’s inequalities.

Soon after, it was realized that the saturation conjecture was sufficient to prove Horn’s inequalities.

In 1998, Knutson and Tao published their proof.

The argument they made in this paper was refined by a 2013 theorem of a different ARY team: Anderson, Richmond, and Yong. They showed that the analogous statement is true for the Littlewood–Richardson polynomials: $C_{\lambda,\mu}^\nu(Y)=0$ if and only if $C_{N\lambda,N\mu}^{N\nu}(Y)=0$ for all $N$.

The major innovation made by the new ARY team (Adve, Robichaux, and Yong) constructed a family of polytopes $P_{\lambda,\mu}^\nu$ with the following properties:

scaling the polytope by a factor of $N$ is the same as scaling the partitions by a factor of N, i.e. $P_{N\lambda,N\mu}^{N\nu} = NP_{\lambda,\mu}^\nu$,

and the crucial bit: $P_{\lambda,\mu}^\nu$ has an integer lattice point if and only if $C_{\lambda,\mu}^{\nu}(Y)\neq 0$

In particular, this implies that the “polynomial saturation conjecture” can be used to reduce the question of $C_{\lambda,\mu}^{\nu}(Y)\neq 0$ to figuring out whether $P_{\lambda,\mu}^\nu$ is the empty polytope. And this, finally, is a problem which is known to be solvable in polynomial time, which concludes the proof.

------

[ * The dates listed above are the publication dates of the papers that the two teams wrote. “So that tells you something about publishing in mathematics”, Yong says. Perhaps, but... I’m not sure what. I’m assuming that what he was getting at is this: The names in the latter team are nothing to scoff at, by a long shot; I mean, I have heard all five of these names before in other contexts. But the prestige associated to the names in the former team might have made that paper subject to less scrutiny than the latter. Or perhaps he just meant that the capricious turns of fate can turn what “should be” a short procedure into a long one. ]

#math #maths #mathematics #mathema #algebra #combinatorics #algebraic combinatorics #geometry #symmetric functions #complexity #caplus #caplus2017

7 notes · View notes

craigbrownphd-blog-blog · 6 years ago

Text

Free Textbook: Probability Course, Harvard University (Based on R)

A free online version of the second edition of the book based on Stat 110, Introduction to Probability by Joe Blitzstein and Jessica Hwang, is now available here. Print copies are available via CRC Press, Amazon, and elsewhere. Stat110x is also available as an free edX course, here. The edX course focuses on animations, interactive features, readings, and problem-solving, and is complementary to the Stat 110 lecture videos on YouTube, which are available here. The Stat110x animations are available within the course and here. For more information, visit Stat110 at Harvard. A 10-page cheat sheet summarizing the content, is available here. For more free books, visit this page. Table of Contents 1. Probability and Counting * Why study probability? * Sample spaces and Pebble World * Naive definition of probability * How to count * Story proofs * Non-naive definition of probability * Recap * R * Exercises 2. Conditional Probability * The importance of thinking conditionally * Definition and intuition * Bayes' rule and the law of total probability * Conditional probabilities are probabilities * Independence of events * Coherency of Bayes' rule * Conditioning as a problem-solving tool * Pitfalls and paradoxes * Recap * R * Exercises 3. Random Variables and Their Distributions * Random variables * Distributions and probability mass functions * Bernoulli and Binomial * Hypergeometric * Discrete Uniform * Cumulative distribution functions * Functions of random variables * Independence of rvs * Connections between Binomial and Hypergeometric * Recap * R * Exercises 4. Expectation * Definition of expectation * Linearity of expectation * Geometric and Negative Binomial * Indicator rvs and the fundamental bridge * Law of the unconscious statistician (LOTUS) * Variance * Poisson * Connections between Poisson and Binomial * *Using probability and expectation to prove existence * Recap * R * Exercises 5. Continuous Random Variables * Probability density functions * Uniform * Universality of the Uniform * Normal * Exponential * Poisson processes * Symmetry of iid continuous rvs * Recap * R * Exercises 6. Moments * Summaries of a distribution * Interpreting moments * Sample moments * Moment generating functions * Generating moments with MGFs * Sums of independent rvs via MGFs * *Probability generating functions * Recap * R * Exercises 7. Joint Distributions * Joint, marginal, and conditional * D LOTUS * Covariance and correlation * Multinomial * Multivariate Normal * Recap * R * Exercises 8. Transformations * Change of variables * Convolutions * Beta * Gamma * Beta-Gamma connections * Order statistics * Recap * R * Exercises 9. Conditional Expectation * Conditional expectation given an event * Conditional expectation given an rv * Properties of conditional expectation * *Geometric interpretation of conditional expectation * Conditional variance * Adam and Eve examples * Recap * R * Exercises 10. Inequalities and Limit Theorems Inequalities Law of large numbers Central limit theorem Chi-Square and Student-t Recap R Exercises 11. Markov Chains * Markov property and transition matrix * Classification of states * Stationary distribution * Reversibility * Recap * R * Exercises 12. Markov Chain Monte Carlo * Metropolis-Hastings * Recap * R * Exercises 13. Poisson Processes * Poisson processes in one dimension * Conditioning, superposition, thinning * Poisson processes in multiple dimensions * Recap * R * Exercises A Math * Sets * Functions * Matrices * Difference equations * Differential equations * Partial derivatives * Multiple integrals * Sums * Pattern recognition * Common sense and checking answers B R Programming * Vectors * Matrices * Math * Sampling and simulation * Plotting * Programming * Summary statistics * Distributions C Table of distributions Bibliography Index http://bit.ly/2M632nM

0 notes