#combinatorics

[todays-xkcd]

Look, you can't complain about this after giving us so many scenarios involving N locked chests and M unlabeled keys.

D&D Combinatorics [Explained]

Transcript

[Cueball, Megan, Ponytail, White Hat, and Knit Cap are sitting at a table. Everyone is looking at Cueball. Ponytail is facepalming. The table is covered in sheets of paper and assorted dice.] Cueball: I grab 2 of the 10 arrows without looking and fire them, hoping I didn't grab one of the 5 cursed ones. Did I? Ponytail: Sigh. Umm. Okay. Ponytail: Roll... Uh... Hang on... Ponytail: Roll 3d6 and a d4. You need... 16 or better to avoid the cursed arrows.

[Caption below the panel:] I got way more annoying to play D&D with once I learned that our DM has a combinatorics degree and can't resist puzzles.

[knotty-et-al]

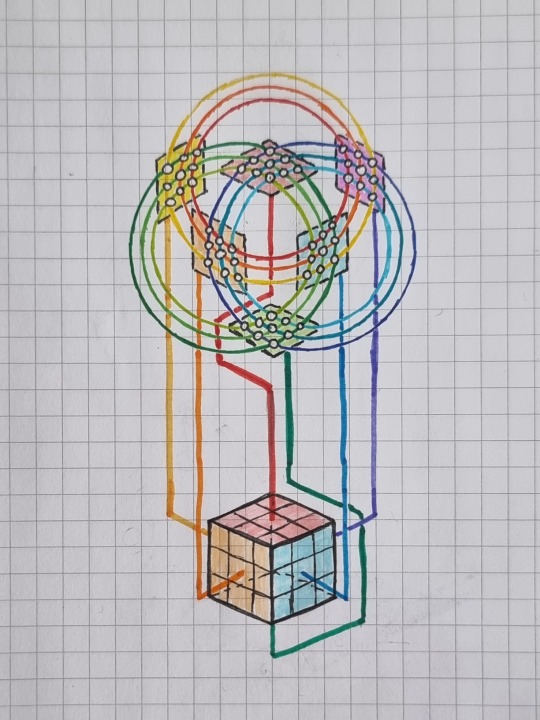
Visualization of the Rubik's cube

[dreams-of-soft-rain]

the proof is left as an exercise for the reader <3

[mentalknot]

Math Research... Once More?

If I've learned anything this semester, it's that I fail to be chill about anything... especially math.

I didn't expect that my friend's invite a math talk would spark multiple months of joyous combinatorial conversation. I didn't expect to meet a group of kind mathematicians, who welcomed a naive undergrad to their seminars, to their dinners, to the niche beauties of their research area.

I didn't expect those weekly seminars to slowly heal trust in my mind.

However, here we are. I've been exceptionally lucky -- more than one can suitably write. A few weeks ago, in a moment where I was fully ready to give up, drop out, and sign myself into a long-term facility (if they even exist anymore)... a professor offered me a lifeline:

"Reach out to my advisor, he's quite kind, and may have an idea of someone who's available to work with you for the summer."

Her advisor is the top person in his field -- there's no way he'd have the time of day for me... right?

He offered me a problem, asked if I had any ideas of conjectures or results on further generalizations...

I spent three weeks, poured over his books, papers, and any related works I could find in the field. Outside math, my grandmother had a health scare, then my housing fell through for May.

I clung to the question like it was my only comfort -- it was.

Eventually, as I continued to worry about "accidently ghosting" the kind professor, the ideas fell right in front of me. I wrote rough notes in LaTeX, summarized in an email... and replied to the professor.

He offered to meet.

Had I conjectured well? I trust my own ideas... rather I don't trust myself as the sender. Nonetheless, I must now prepare for our chat. He asked for my note sheet as well... which was... organized to my own liking, so I'm cleaning some things.

I still have no idea where I'll be living for one month after finals, where I'll make money (feels rude to ask in the current political climate...), but I know one thing...

If I work with him, I'll be around mathematicians who I've come to trust and care about -- I'll have a home in every emotional sense... and I'll have math... math that makes me feel sane...

When I worked on his problem... my mind felt truly free, truly functional, truly happy... for the first time in 10 years.

Here's to hoping I don't fall on my face once more.

[positively-knotted]

Some Basic Combinatorics Via Not-So-Basic Topology

Proposition. Let P(r; n,k) be the number of partitions of an integer r into n non-negative integers less than or equal to k. Then P(r; n,k) = P(r; k,n).

This is very easy to see with Young diagrams (count columns vs rows). It's also very difficult to see with topology, but that's more fun. This is probably going to be a bit long, but I think the pay-off is worth it.

The standard construction of (real) projective space Pⁿ is to call it the space of 1-dimensional subspaces of Rⁿ⁺¹. This generalises pretty naturally to the "Grassmann manifold" Gr(n; n+k) of n-dimensional subspaces of Rⁿ⁺ᵏ, so Pⁿ = Gr(1; n+1). Hopefully you believe that Gr(n; n+k) is still a compact nk-manifold. If you want, it's also the quotient O(n+k)/O(n) x O(k).

As well as being a manifold, this is naturally a CW complex. Let's think about how. For each point in Gr(n; n+k) (that is, n-dimensional subspace), it has a unique orthonormal basis where the final non-zero coordinate of each basis vector is positive (easy linalg exercise). Taking this basis, we let d_1,...,d_n be the the "dimension" of the basis vectors (i.e. the position of their final non-zero coordinate, so that (-1,2,0) is 2-"dimensional"). We can assume these are strictly increasing by permuting them. Thus, to each point in Gr(n; n+k), we are associating a unique list of n increasing integers between 1 and n+k.

Let e(d_1,...,d_n) be the subset of Gr(n; n+k) which give those integers. This is actually an open disc of dimension Σ(d_i-i)! Why? To choose the first basis vector, we can pick any unit vector in the upper half-space of dimension d_1. That is, we have a choice in the hemisphere=disc of dimension d_1-1. To choose the ith, we have a choice in a hemisphere=disc of dimension d_i-1, but we have to be orthogonal to the i-1 vectors we have already chosen, giving a choice in a disc of dimension d_i-i. A product of discs is a disc, and we're done!

Checking that this is actually a CW decomposition is kinda tricky, but also unenlightening, it just is true. So let's count how many cells of each dimension it has. An r-cell corresponds to a choice of partition r = Σ(d_i-i), where 1 ≤ d_1 < ... < d_n ≤ n+k. Equivalently, it is a choice of partition r = Σe-i, with 0 ≤ e_1 ≤ ... ≤ e_n ≤ k, by setting e_i = d_i-i. So the number of r-cells is exactly P(r; n,k)!

We're getting close! The final observation is this. Choosing a n-dimensional subspace is equivalent to choosing its orthogonal complement. That is, the map V → V^⊥ is a natural diffeomorphism between Gr(n; n+k) and Gr(k; n+k), and also a CW-isomorphism. (True because everything is naturally defined; slightly tedious to check.) In particular, it has to match up the number of r-cells, so P(r; n,k) = P(r; k,n)! No Young diagrams necessary.

I think this is kinda neat. It's also weird because these Grassmann manifolds completely classify vector bundles on compact manifolds and are how you define characteristic classes, so secretly under all of that differential topology there's really hard partition problems going on.

[kneadingmaths]

A very standard combinatorics problem about counting paths. Well then, how many?

[squishmallow36]

My combinatorics class today:

[m---a---x]

Inspired by all the newly created communities i have also created one about the topic closest to my heart: Foundational Mathematics

It is inteded for all types of posts about and from people of all kinds of backgrounds interested in the topic.

Please share with anyone you think might be interested. If you want to be added comment on this post, so I can add you.

[heyitscoffeetime]

List of type combinations that don't yet have a Pokémon:

(As of April 2025)

Normal/Rock

Normal/Bug

Normal/Steel

Normal/Ice

Poison/Ice

Ground/Fairy

Rock/Ghost

Bug/Dragon

Fire/Fairy

[educationaldm]

I can confirm that the mathematics in this XKCD comic is correct (although I cheated a little with AnyDice.com because it was late). The probability is 2/9 of avoiding the cursed arrows.

[thegoodduckfan]

Imagine going to a comics convention and waiting in line for two and a half hours to meet your favorite (living) comic book artist, and you end up talking to him about math... couldn't be me.

[desmos-calculator]

Oh, Martin Gardner...

Thanks

[blake447]

Combinatorics of n-Dimensional Chess

So my current project of n-dimensional chess has involved perhaps, some of the most interesting combinatorics I've ever handled. Let's talk about them! It's a perfect showcase of what I think are the 3 most important parts of math 1.> Start with simple, easy examples 2.> Break large problems into smaller parts 3.> Shift your perspective and abstract problems in a way that they are easier to deal with, while retaining a way to shift back once you've solved it to reapply what you've done. So, let's first start with the problem. Here's a piece in 5D chess known as a unicorn. It can move along any triagonal, which means it has to pick 3 out of the 5 dimensions available. in 4D time travel chess, it actually gets to move in 6 dimensional space, but it was originally introduced in space chess, a 3D variant. My point here is that n-dimensional chess means that we have to be able to list these kinds of moves for a lot of different dimensionalities, and hard coding them quite simply isnt an option. So, we turn to combinatorics!

We'll start with point 1.> by starting with our easiest example. Let's take a look at a bishop's movement in 2D space first to get a good baseline. The directions a bishop can travel along in 2D space are as follows

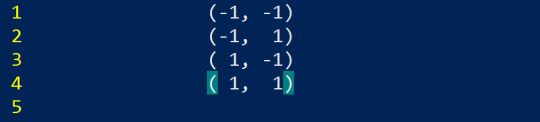
Now I purposely arranged this in a way that if we replace negative numbers with 0, we get

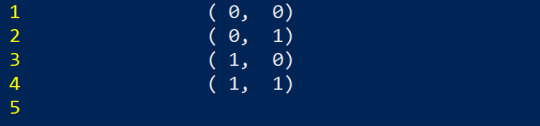
And hey! That's just counting in binary! Which makes sense, because we only have two choices, positive and negative. Once we move up to 3D space, we can actually re-use this tactic as well. Let's list all the possible combinations of directions in 3D space first, without worrying about the sign. This is what I mean in part 2.> by breaking complex problems into smaller ones, in this case breaking the movement into directions and signs.

Basically, now we can take each one of these 3 possibilities and just apply our same trick by ignoring whichever part the 0 is in. And this works for triagonals and quadragonals in higher dimensional space as well. This makes iterating through signs the easier part Of course, that means the other half is going to be the hard part. Now, with diagonals it isn't too bad. Lets look at diagonals in 5D space. Get ready because this one is a bit more of a jump

Basically what I'm doing here is I'm starting with each 1 as far left as possible, and sliding them over repeatably. not the best explanation, but its doesn't matter because this method doesn't extend well to triagonals very well (choosing 3 directions at once). Instead, we take a shift of perspective, demonstrating point 3.> Instead of representing this as a series of 1's and zeros, we simply represent the *position* of each 1. For example

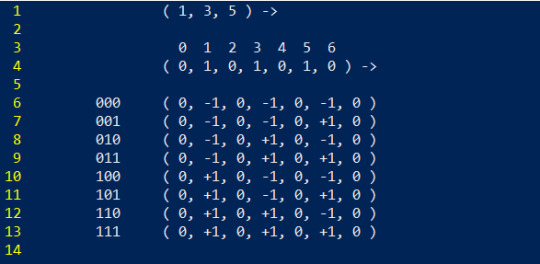
We have a 1 in the 0th and 3rd locations, so we can simply represent this as just (0, 3). Suddenly, instead of trying to figure out how many ways there are to arrange 1's and 0's, we are asking how many ways can we choose 2 numbers out of 0-4. Now, there is a slight catch in that (0, 3) and (3, 0) are the same thing, so when counting them order doesn't matter, making this a simple combination problem. However we don't just want to count them, we also want to iterate over them. Lets try to generate all possible triagaonals within 7D space. That means we want to choose 3 numbers ranging from 0-6. We start with our easiest one

In order to avoid repeats (no pun intended) we maintain a strict order that is always increasing. Each number should always be larger than the previous one. To iterate through new combinations, we simply increase the last number until we can't anymore.

Now at this point, we can't increase the last number any more, so we increase the second to last and start over

And since the number after 2 has to be larger than 2, the smallest number we can roll over to is 3. From here we continue. Basically, it turns this complicated problem into a type of counting game. Just like with regular numbers, we increase the last one until it can't go anymore, then we increase the next one over and restart, just instead of restarting to 0, we restart to the smallest allowed number that keeps things in order.

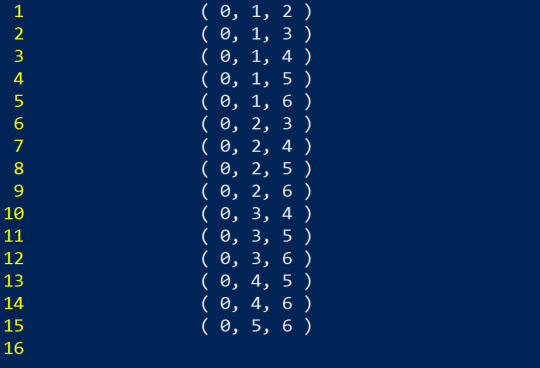
And at this point, we now have to increase our first number. I'll go ahead and finish this up despite it being pretty long, so that we can make sure we have all the possibilities

Now if we do some quick calculations for how many combinations we have of 3 numbers out of 7 total we get 3 choose 7 = 7! / ( 3! * (7-3)! ) = 7! / ( 3! * 4! ) = (7 * 6 * 5) / (3 * 2 * 1) = (7 * 5) = 35

Which is exactly how much we counted to! There are a few reasons we know there aren't any repeats but this has gotten long enough, and I can't quite articulate them off the top of my head. From here we convert back into 1's and 0's, then we count up in binary for each one of them to get the sign permutations. To wrap things up, I'll finish up by demonstrating all those sign permutations for one of these direction combinations. As stated in point 3.> we can translate back from our abstraction back to the original problem, so we can apply the smaller part that is generating the sign permutations.

There we go. A little bit of a mess, but that's it! And that's how I generate arbitrary m-agonals in arbitrary n-dimensional space for my chess engine. Finally, here's a picture of a queen's movement allowed to move along any agonal up to heptagonals (seven!) on a 7D board generated in a precursor to my current iteration of nDimensional chess

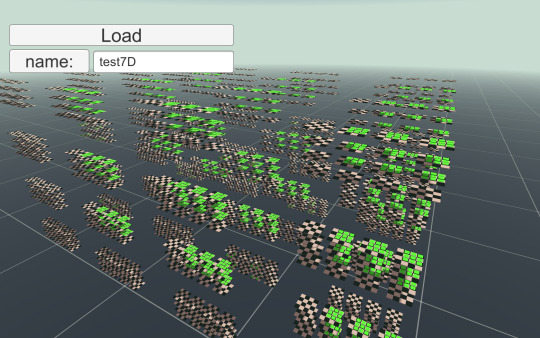
Y'know, not that anyone would ever play that lol. Here's a bishop on the same board, which is (somewhat) more... manageable lol.

And that's all I got! this math right here is the bread and butter of what makes n-dimensional chess possible! and is potentially one of my favorite problems I've worked on.

[mentalknot]

I’ll always be amazed by the kindness of combinatorialists. Despite my lack of background eight months ago, they welcomed me to their seminars, taking time to explain various concepts.

I was terrified of my own mind, and they assured me that I was not ill, rather dealing with naïve creativity/intuition. They shared stories of historical mathematicians, of eccentric philosophers, and slowly… I felt calm again.

They’ll never know how much these conversations helped me, how the term “academic family” meant the world, given recent events in my personal life.

I hope to repay their kindness by engagement and helping in any way I can, and I intend to pass along their lessons to younger students when I’m able.

[cecilias-cool-stuff]

Today in "Wow, people in the 60s were really Like That":

[spectruminterests]

I used the poll options to narrow down choices for the ball/toy pit poll

The "Fandom" account on tumblr has posted an April Fool's Day set of polls asking people to guess how many of 3 different kinds of toys and how many toys total are in a container. Using the numbers given in the polls, I've found five possible answers to all the poll questions in which the numbers of each kind of toy add up to the total:

247 crabs + 277 horses + 235 paws = 759 objects total

247 crabs + 277 horses + 249 paws = 773 objects total

247 crabs + 313 horses + 242 paws = 802 objects total

239 crabs + 299 horses + 235 paws = 773 objects total

283 crabs + 277 horses + 242 paws = 802 objects total

Feel free to use this information along with your own (or someone else's, no judgement!) size/volume estimations to make your guesses! Or just guess, there are no rules!

Explanation under the readmore:

Each poll gives four potential answers. Assuming that the correct answers for how many of each object there are and the total number of objects are given as options in the polls, this means that the correct total would have to be the sum of three of the answers given in the polls about the individual objects, one from each poll. There are sixty-four possible combinations of one answer from each of the three four-option individual object polls. (If you start with all the combinations you have when you pick the first answer in the first poll and the first answer in the second poll, there are four potential combinations, one for each choice in the third poll. You have the same four choices and four combinations if you choose the first option in the first poll and the second option in the second, and so on for the third and fourth; this gives four combinations for each of the four choices in the second poll, so there are sixteen combinations for each option in the first poll, giving a grand total of sixty-four possible combinations.) I used a spreadsheet (linked here) to find what each of those sixty-four combinations added up to, then found the combinations which added up to a number that was presented in the "how many objects total" poll.