#symmedian point

[squareallworthy]

Triangle Tuesday 5: The symmedian point, how a point can have a BFF, an aside, and lots of cool constructions

Let's start with the medians. You remember the medians, right? They are the lines that connect a triangle's vertices to the midpoints of the opposite sides. The all meet at the centroid, G. Next we'll add the angle bisectors, which split the angles at each vertex into equal parts. Then we'll reflect the medians across the bisectors to form the symmedians. They all meet at a point K, the symmedian point.

Here they are, with the medians in red, angle bisectors in gray, and symmedians in green. And no, I don't know why the letter K is traditionally used for the symmedian point. If anyone can tell me, please do.

(Although the three angle bisectors cross at the incenter, the process of locating the symmedian point does not just amount to reflecting the centroid through the incenter. As you can see, the line connecting G and K doesn't quite pass through I. This triple line reflection is not equivalent to a point reflection.)

In looking at the symmedian point, we are jumping forward many centuries from the points we looked at before. The incenter, centroid, circumcenter, and orthocenter were all known to the ancient Greeks, but the symmedian point was not noted until the 19th century. Émile Lemoine proved its existence in 1873, and for that reason it is sometimes called the Lemoine point.

A proof is very simple, but I'd like to keep to only one proof in this post, so I want to make it a good one. I want to make it more general. So let's first take a little wider view of what we've done here with the symmedians.

In case it is not clear, when I say that we reflect a median across an angle bisector, I mean that we draw a line from a vertex that makes the same angle with the bisector as the median makes with the bisector, but on the opposite side. The symmedian, then, is just the line that is symmetrical to the median.

Also, remember that lines drawn from a vertex of a triangle to intercept the opposite side are called cevians (pronounced ˈtʃeviən, CHAY-vee-un). All of the lines in the drawing above are cevians.

Two cevians drawn from the same vertex that form the same angle with the angle bisector are said to be isogonal (iso meaning "same" and gon meaning "angle"). Every cevian has an isogonal line, and the angle bisector is its own isogonal line.

And speaking of cevians, let's also remember Ceva's theorem. Each cevian passing through a point P cuts a side of the triangle into two segments, and the ratios of those two segments are related by this equation:

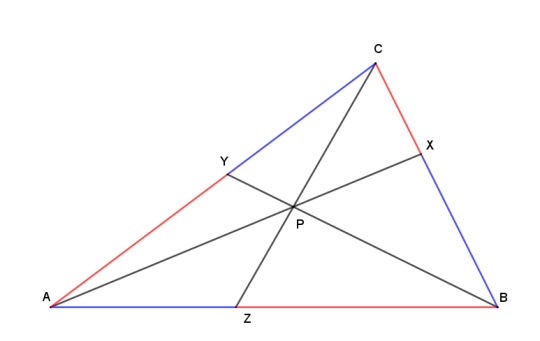
AZ/ZB * BX/XC * CY/YA = 1

So the red and blue segments on each side do not all have the same ratio, but the product of the three ratios is 1.

With that in mind, we can prove not just that the symmedian point exists, but something more general and powerful:

Theorem: if three cevians drawn from the vertices of a triangle coincide, their isogonals also coincide.

For proof, let's just consider one of the cevians and its isogonal line.

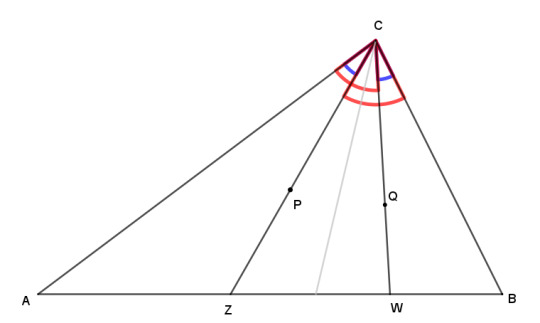
Here we have a cevian through point P meeting side AB at Z, and its isogonal meeting AB at W. Point Q is just there for kicks right now.

Because CZ and CW make the same angle with the bisector (in gray), they also make the same angles with the adjacent sides, so the blue angles are equal, as are the red angles. So the ratio of blue angles to red angles are the same, meaning

sin ∠ACZ / sin ∠ZCB = sin ∠WCB / sin ∠ACW

and so by the law of sines,

AZ / ZB = WB / AW.

This is just the ratio we want in order to apply Ceva's theorem to the reflections of the cevians we started with. We can do this for all three vertices, and then substitute our results into the equation above, showing that the ratios for the segments of the isogonals all multiply to 1, and that therefore the isogonals coincide.

So yes, the construction used for the symmedian point always works, for any point. A point Q constructed in this way from a point P is called the isogonal conjugate of P. This relationship is reflexive (by contruction), so if Q is the isogonal conjugate of P, then P is the isogonal conjugate of Q. Or, as I like to think of it, P and Q are BFFs.

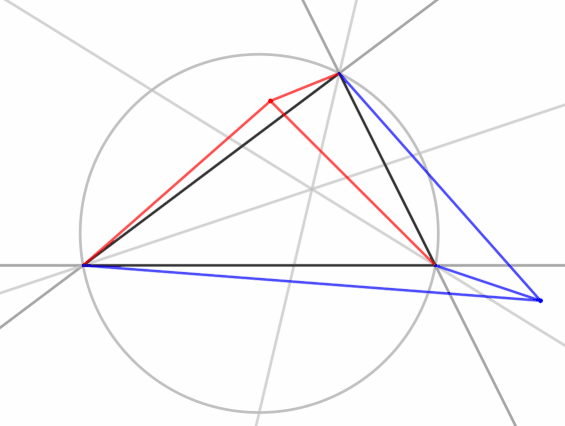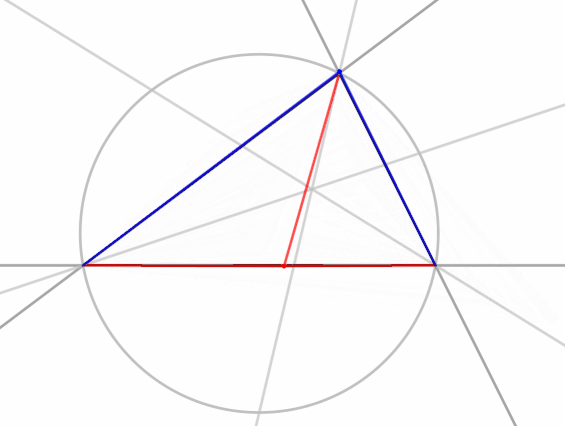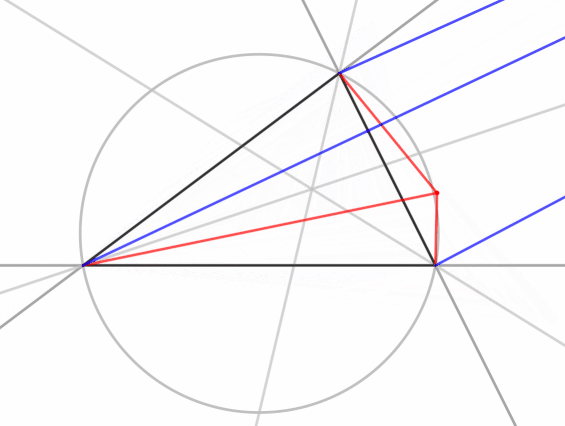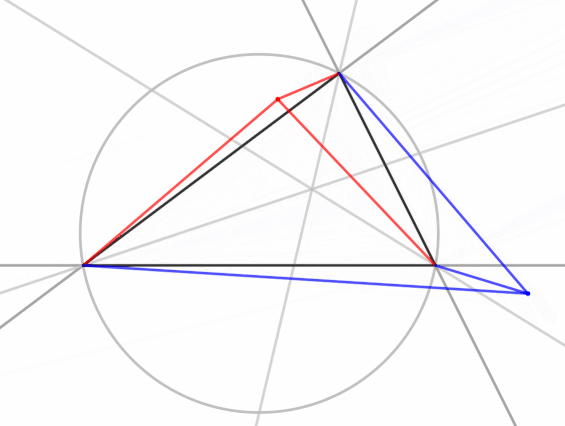
Isogonal conjucation maps points in the inside of a triangle to points inside the triangle. Isogonal conjugates of points on the circumcircle go to infinity. In the animation, you can see the blue point go through a discontinuity twice as the red point crosses and recrosses the circumcircle.

So the centroid and symmedian point are isogonal conjugates, and as you might have figured out, the incenter is its own isogonal conjugate.

What else can we say about the symmedian point? Well, it has a ton of cool alternate constructions. There are too many of them to prove, so I'm just going to show you a bunch.

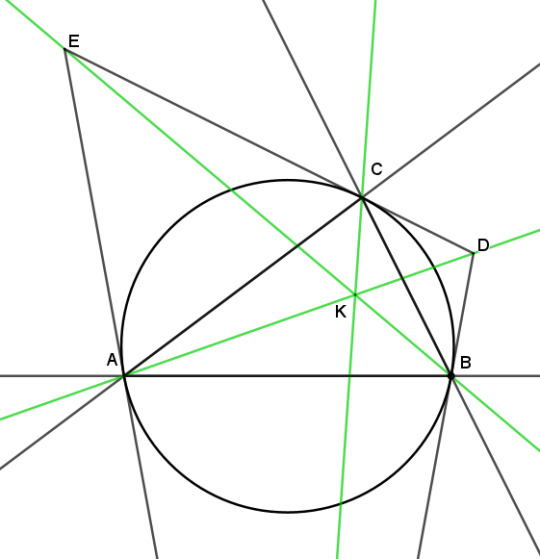
The symmedian point is perspective to ABC and the tangential triangle.

Draw tangents to the circumcircle at A, B, and C, and let them intersect at D, E, and F. Triangle DEF is the tangential triangle to ABC, and the lines AD, BE, and CF are symmedians.

When corresponding vertices of two triangles are colinear with a single point like this, we say that the triangles are in perspective, and the point is the center of perspectivity or perspector of the triangles.

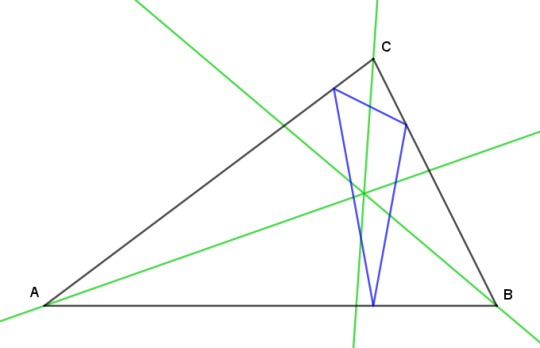
Each symmedian bisects a side of the orthic triangle.

Furthermore they bisect all the line segments spanning the triangle that are parallel to the sides of the orthic triangle. All such lines are called antiparallels. And why are they called that? Okay, sure, let's have a little aside on antiparallel lines.

Euclid defines parallel lines as lines in a plane that do not meet each other in either direction. His test for whether lines are parallel is to cross them with another line. Then if the alternating angles are equal, the lines are parallel.

The upper left drawing shows such a situation. The black line crosses the two blue lines making equal alternating angles, therefore the two blue lines are parallel.

The upper right shows two lines that make the same angle with the black line, but now one of them faces away from the other line rather than toward it. In this situation, the red and blue lines are said to be antiparallel with respect to the black line. Parallel lines are parallel regardless of any other line, but antiparallel lines are only ever relatively antiparallel. They can only be said to be antiparallel compared to some other reference.

The lower left drawing shows how a pair of lines can be the reference. A pair of lines (red and blue) are antiparallel to another pair of lines (black) if they are antiparallel to their angle bisector (gray). In that case, the blue angles are equal.

The lower right drawing shows how this applies to triangle geometry. How do you find an antiparallel line in the first place? By reflecting one of the sides across the bisector of the opposite angle. The solid black segment at the bottom of the triangle defines parallels for this side, of which the blue line is an example. And the dashed black segment, which is the reflection of the solid segment, defines the antiparallels for this side, of which the red line is an example. Each side of a triangle defines such sets, all of which together are called the parallels and antiparallels of the triangle.

With that in mind, let's show how this applies to the symmedian point.

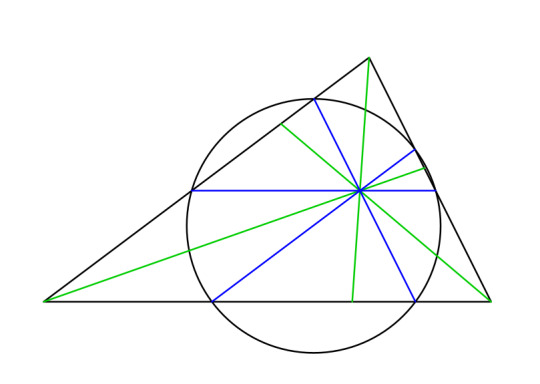
Parallels drawn through the symmedian point intersect the sides in six concyclic points.

Antiparallels drawn through the symmedian point intersect the sides in six concyclic points.

You didn't think that aside was for nothing, did you? This concludes our bit on parallels and antiparallels. Onward!

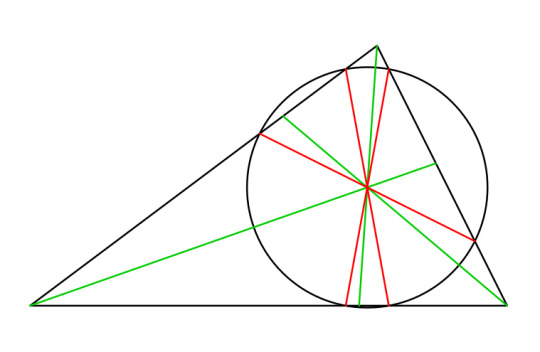
Circles drawn through the symmedian point and pairs of vertices intersect the sidelines in six concyclic points.

Since we did both kinds of lines, why not circles?

This nonsensical figure is somehow true.

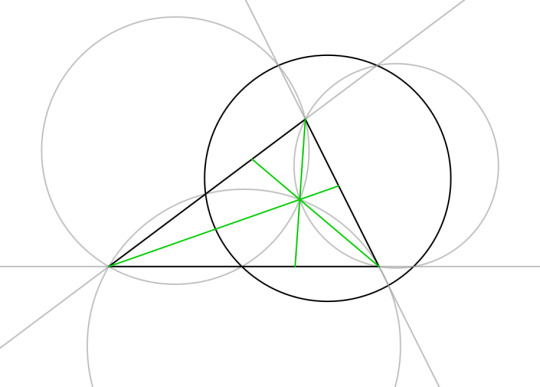
Draw squares on each side of triangle ABC. Draw circles through the vertices of the triangle and the adjacent two vertices of the squares. The lines connecting the centers of those circles and A, B, and C are symmedians.

It's even still true if you draw the squares the other way.

Same as above, but the squares are draw toward the inside of the triangle instead of away from it.

Draw a line connecting the midpoint of an altitude from a vertex with the midpoint the the opposite side. The line passes through the symmedian point.

in case you wanted to locate the symmedian point without drawing any symmedians.

Let P be a point on the circumcircle but not a vertex. Let Pa, Pb, and Pc be its projections onto the sides. Then one of the three projected points bisects the line segment joining the other two iff P is on a symmedian.

This of course is a Simson line, which we saw when we looked at the circumcircle.

The symmedian point is the centroid of its own pedal triangle.

It's also the only point that is the centroid of its own pedal triangle. As a corollary, the centroid of a triangle is the symmedian point of its antipedal triangle.

That links the symmedian point back to the centroid again, so I think I'll stop here. There are other points the symmedian point connects to, and more I could say about isogonal conjugates, but that will have to wait for another day.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.

[mathhombre]

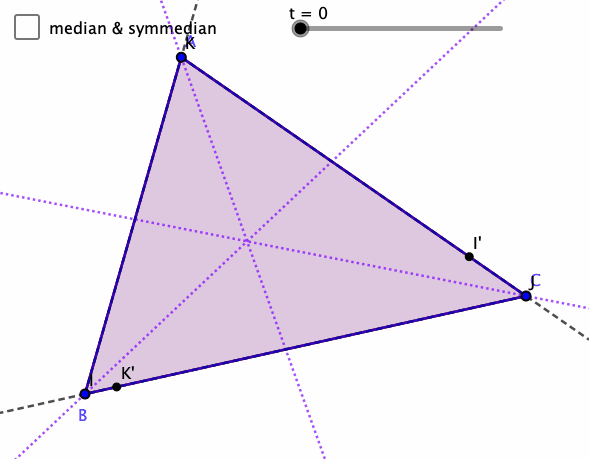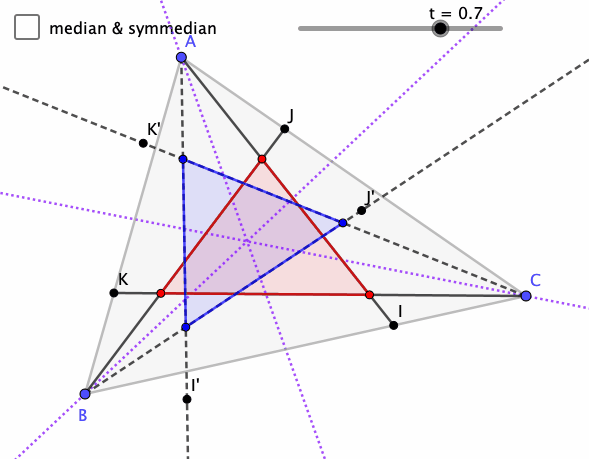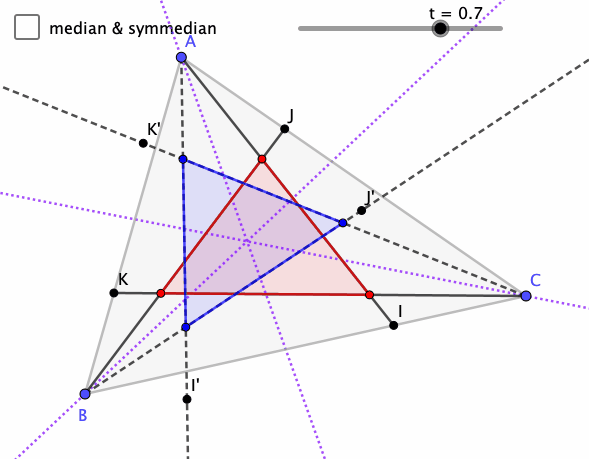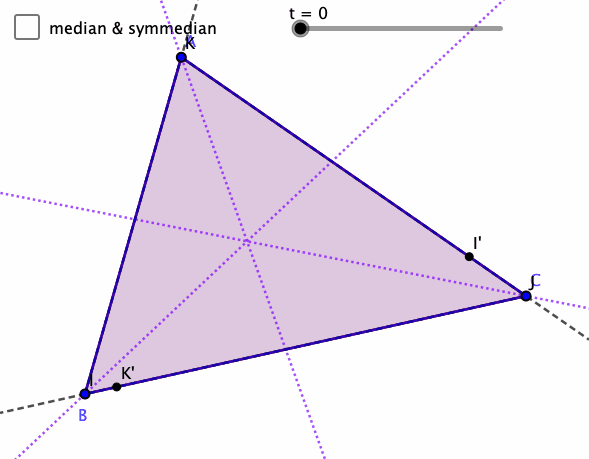
Symmedian

Day 2 of Mathober is Symmedian.

Had to remind myself what that means, the reflection of the median across the angle bisectors (isogonal to the medians). And just like the medians are concurrent, then so are the symmedians, and their intersection is the isogonal conjugate to the centroid (the intersection of the medians).

There's an idea called the trilinear coordinates for a point in a triangle, and the trilinear coordinates for the symmedian intersection are the inverse of that for the centroid. I'm not sure how to produce the trilinear coordinates given a point, nor find a point from the trilinear coordinates. There's always more to learn.

This sketch generalizes the median to the corresponding points parameterized by t, and those segments isogonal segments. Pretty fascinating to me.

What do you notice and wonder?

Sketch is on GeoGebra.

[squareallworthy]

Triangleposting index

This is an index to my series of Triangle Tuesday. It's mainly for my own reference, but fellow initiates to my cult of triangles may also find it useful.

1. The centroid, Ceva's theorem, and median and antimedian triangles

2. The circumcenter, pedal triangles, Simson lines, and Steiner's deltoid

3. The orthocenter, the Euler line, and orthocentric systems

4. The incenter, incircle, and excircles

5. The symmedian point, isogonal conjugates, parallels and antiparallels

6. More on parallels and antiparallels

7. Trilinear coordinates

8. The nine-point circle

9. The Nagel point

10. The Spieker center

11. The Gergonne point

12. The Conway circle

13. Inversion and the far-out point

[squareallworthy]

It's Triangle Tuesday! A triangle, its centroid, a theorem, and two bonus triangles.

Greetings, seekers of triangle knowledge. Today I'm going to talk about the centroid.

Among triangle centers, the centroid is, at first glance, maybe a bit underwhelming. Take a triangle ABC. Let the midpoints of the sides be M_a, M_b, and M_c. Draw a line from each vertex to the opposite midpoint. The three lines cross at a point G. And that's the centroid.

Very simple. Simple almost to the point of banality. Don't get me wrong - the centroid is a great point. It's just not very flashy in its construction, and the fact that it exists doesn't seem at all deep. Later on, we can show how the centroid relates to other things, such as the symmedian point, the Euler line, and the nine-point circle. But for now, it's kind of hard to appreciate the centroid on it own. Let's do what we can do now, before getting into that other stuff, to see why the centroid is interesting.

It's not at all difficult to prove that the lines meet at one point, but the proofs I've looked at aren't all that enlightening. You draw a line and look at some parallel lines, and you say, "mmm, okay, that checks out, that's a proof all right," but it doesn't feel like you've learned much.

Even before proving that the lines are all coincident, it seems obvious that they should be. Each line cuts the triangle into two equal parts, and so when you draw two of them, the point where they cross is the middle of the triangle, measured two ways. So it just makes sense that the third line has to go through the same point, right?

Let's see if we can follow our intuition on this to get at something more fundamental. The lines that connect the vertices to the midpoints of the side are called medians. In general, lines like this that extend from a vertex to the opposite side of the triangle are called cevians (pronounced ˈtʃeviən, CHAY-vee-un). Are the medians really all that special among other cevians? What if instead of marking the midpoint of each side, dividing it into two segments in a 1:1 ratio, we mark a point that divides the side in a 1:3 ratio, going counterclockwise around the triangle? If we then draw the cevians, what do they look like?

Not surprisingly, the they aren't coincident. They outline a triangle (in red) that looks like the original triangle, but smaller and tilted counterclockwise. If we divided in a 1:3 ratio going clockwise, we would get a clockwise-twisted triangle. And if we move the marked points back and forth, sure enough, only when the points are halfway along the sides do the three cevians cross at one point.

And if we take the crossing point of two cevians, and then draw the third line through that point? Where does that hit the opposite side? Here I'll go back and draw that with a dashed line on the 1:3 ratio counterclockwise drawing:

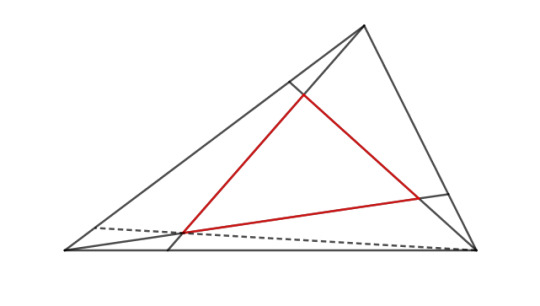
It lands pretty close to the vertex. Somehow that point has to balance the 1:3 ratio we used to measure the other points, but it's not clear exactly how.

So how are coincident points connected to the place where we cut the sides? Let's get a bit more formal. Let's have a triangle ABC, and a point P that is not located on any of the sides of the triangle. We'll draw cevians from the vertices through P, and they will cross the sides of the triangle at D, E, and F.

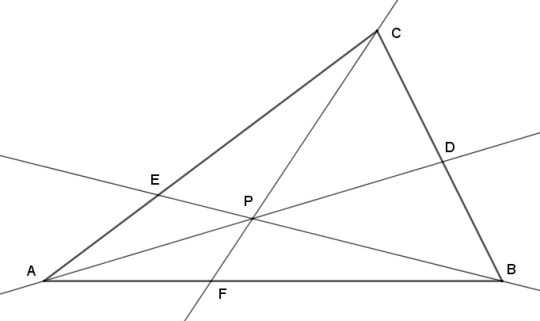
So we would like to know where F, for instance, cuts line AB, and how it relates to the other points. Or, to put it another way, if we knew the ratio of the length of AF to FB, and the same for BD to DC, could we say what the ratio of CE to EA is? Conversely, if we have a triangle with three cevians cutting the sides at D, E, and F, and we knew all the ratios AF/FB, BD/DC, and CE/EA, could we say whether the cevians are coincident or not?

It's easy to get lost here with statements made up of long strings of segments. If you are like me, your eyes start to glaze over when you see that and you don't learn anything. So let's lay out a plan for figuring this out. We are looking for some information about ratios of line segments. To do that, it would be helpful to have some similar triangles, because similar triangles have all the same angles, and differ only in size and orientation. So if you know something about the ratio of two sides of a triangle, you know the same thing about the corresponding sides of a similar triangle.

And a good way to get some similar triangles is to arrange to have them meet vertex-to-vertex between parallel lines, like this:

With this arrangement and a little bit of Euclid (which I won't get into here), we can show that the pairs of angles marked with the same letters are equal. The two triangles with angles α, β, and γ are therefore similar, and we can say that the corresponding sides are in the same proportions -- that is, if we compare the red dashed segment to the blue dashed segment, it is the same ratio as the red solid segment to the blue solid segment. The four colored segments together make a Z-shaped figure, and it is this kind of arrangement of segments that we want to consider as we figure out what's going on with our cevians.

So with that in mind, let's go back to triangle ABC and add a line through A that is parallel to side BC. The new line meets two of our cevians at G and H.

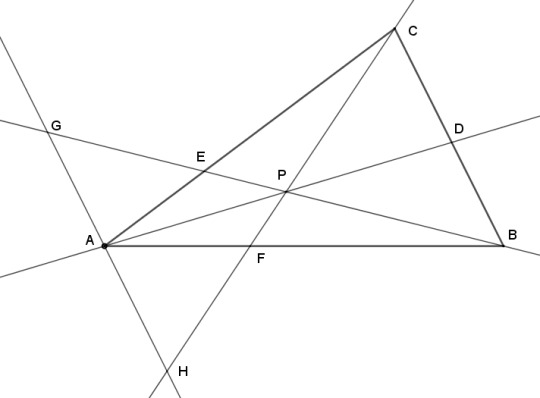
And that creates sets of similar triangles:

AHF is similar to BCF (in red, below)

AEG is similar to BCE (green)

AGP is similar to BDP (blue)

AHP is similar to CDP (yellow)

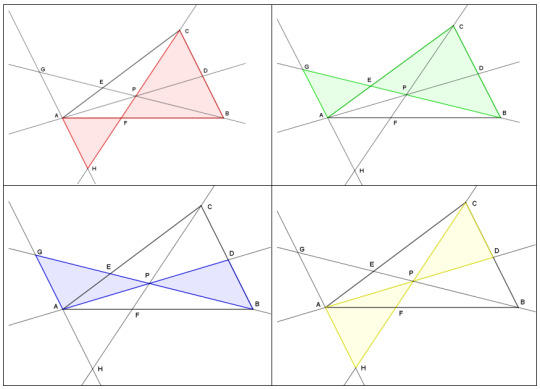
From that, we can get these relationships:

AF/FB = AH/BC (from the red triangles)

CE/EA = BC/AG (green)

AG/BD = AP/DP (blue)

AH/DC = AP/DP (yellow)

We are interested in the ratios that the sides of ABC are divided into, that is, AF/FB and so on. We have two of them above, which I have bolded. We still need to get BD/DC and then shuffle things around to get all of those into one equation.

The two equations above from the blue and yellow triangles have the same right hand side, so we can say

AG/BD = AH/DC

and by reshuffling,

BD/DC = AG/AH.

There's the ratio for the third side. Now let's multiply that together with the equations we got from the red and green triangles:

AF/FB * CE/EA * BD/DC = AH/BC * BC/AG * AG/AH.

Everything on the right cancels out, so if we reorder the things on the left side to be alphabetically nice, we have

AF/FB * BD/DC * CE/EA = 1

which is the first half of what we wanted to know. If three cevians pass through the same point, then they cut the sides into ratios that multiply to 1. What a nice simple relationship to remember!

What about the converse? Can we prove that if three cevians cut the sides in ratios that multiply to 1, they all pass through the same point?

Let's suppose that we have divided the three sides of ABC with points C, D, and E in a way that AF/FB * CE/EA * BD/DC = 1. Then let's draw the cevians BE and CF and say that their crossing-point is called P.

Now, if we draw a cevian from A through P, does it land at D, as our equation says it should? Well, it has to land somewhere, and we'll call that point D'.

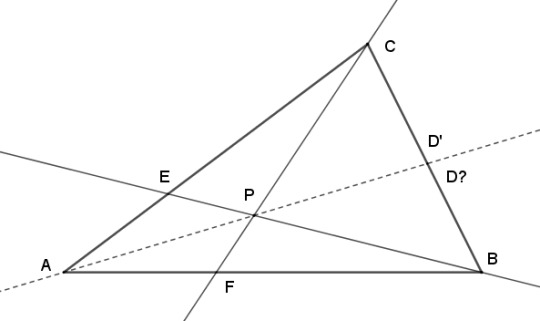
Can we prove that D' = D?

We were given that

AF/FB * BD/DC * CE/EA = 1.

And since we just drew three coincident cevians, we can conclude from what we just proved that

AF/FB * BD'/D'C * CE/EA = 1.

Combining those, we do a little algebraic manipulation:

BD/DC = BD'/D'C

BD/DC + 1 = BD'/D'C + 1

BD/DC + DC/DC = BD'/D'C + D'C/D'C

(BD+DC) / DC = (BD'+D'C) / D'C

But BD+DC is the whole side BC of the triangle, and the same with BD'+D'C. So

BC / DC = BC / D'C

and therefore D = D'. And that's our theorem:

In a triangle ABC, lines connecting the vertices to points on the opposite sides D, E, and F are concurrent if and only if AF/FB * BD/DC * CE/EA = 1

This is called Ceva's theorem, after the Italian mathematician Giovanni Ceva (ˈtʃeva, CHAY-va), who proved it in 1678. But as usual in mathematics the theorem is not named for the original discoverer. That was Abu Amir Yusuf ibn Ahmad ibn Hud, who proved it in the 11th century. (I got the above proof from this website, though I have cut some corners by ignoring signed distances and neglecting the case with an obtuse triangle.)

Given Ceva's theorem, we can trivially prove that the medians of a triangle are concurrent. The midpoints divide each side in the ratio 1/1, so

1/1 * 1/1 * 1/1 = 1

proves the existence of the centroid. There are much more direct ways to prove this, of course, but Ceva's theorem will come up over and over again in the study of triangles so it's worthwhile to get it down now.

Now since we've proved that the medians are coincident, here are some of the properties of the medians and centroid.

The medians divide the triangle into six triangles of equal area.

Each median divides the triangle into two triangles of equal area, because they have equal bases and heights. Therefore

T+U+V = X+Y+Z

but also

Z+T+U = V+X+Y

and subtracting the second from first gives

V-Z = Z-V

V = Z

and similarly for every pair of opposite triangles. But also, X and V have equal bases and heights, so X = V, similarly T = U, Y = Z. Putting that all together shows that all six areas are equal.

The centroid G divides the triangle ABC into three triangles ABG, BCG, and ACG of equal area.

This follows immediately from the previous result, and we can immediately follow that with

The centroid lies on each median at 2/3 of the distance from a vertex to a midpoint.

ABG has the same base as ABC, and 1/3 the area, so it must have 1/3 the height. Those two very straightforward facts give us this less obvious property:

A point X divides a triangle ABC into equal triangles ABX, BCX, and ACX only if X is the centroid.

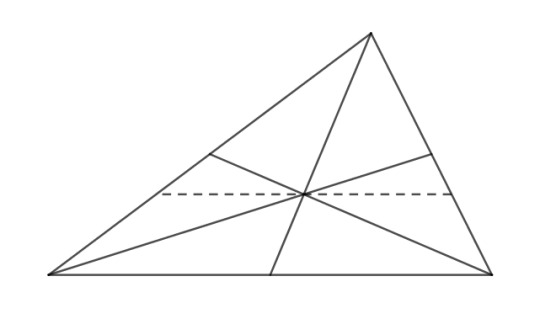
For a triangle ABX to have 1/3 the area of ABC, it must have a height 1/3 that of ABC, so X must lie on the dotted line in the picture, which runs through G. Analogous lines for triangles BCX and ACX must also concur at G.

And, of course, the most famous properties of the centroid, and the reason G is traditionally used to name it, are that the centroid is the center of gravity of the vertices, and also of the area of the triangle. (If you are coming from a physics background, you might object that the centroid of an object is by definition its center of gravity, or center of mass -- that's simply what "centroid" means. To avoid any confusion, I am using a gemometric definition of centroid as the place where the medians cross, and proving that this point is also the center of gravity.)

The centroid is the center of gravity of the vertices.

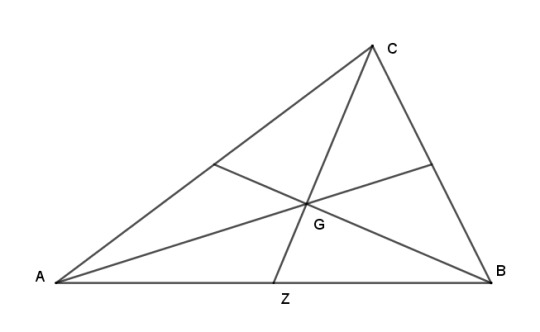
If A and B represent equal masses M, they can be replaced by a single mass of 2M located at Z. The center of gravity of C and Z, then, is a point 1/3 of the way from Z to C, which is G.

The centroid is the center of gravity of the area of the triangle.

Every line parallel to AB can be replaced with a mass Z_1, Z_2, ... at the midpoint of the line. Each of these masses will be located on the median, and so the center of gravity of all these points must also lie on the median. By a similar argument, the center of mass must also line on the other medians, so it must lie at their crossing point. (Yes I admit this is rather handwavy, but a better proof requires integration and I am doing elementary geometry here, not calculus. I have an idea for a proof using purely geometrical methods but I haven't finished it.)

To be complete, I will note that the centroid is not the center of gravity of the perimeter of the triangle. That's a different triangle center, which we will perhaps consider on a different day.

Finally let me introduce two triangles related to the centroid and the medians. The medial triangle, shown in red, is the triangle formed by the midpoints of the sides. The antimedial triangle, shown in blue, formed by lines passing through the vertices A, B, and C and parallel to the opposite side, which meet at A', B', and C'. The anti- part comes from the fact that ABC is the medial triangle of A'B'C.

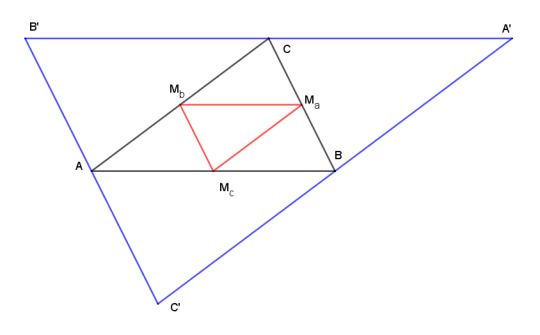
Both of these new triangles are similar to the reference triangle ABC and can be formed by reflecting ABC through a point and scaling up or down by a factor of 2. That point of reflection is, of course, the centroid.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.

[squareallworthy]

Triangle Tuesday 8: the nine-point circle, the deep lore, and did I say nine? I meant, like, fifty-six.

Today we are looking at the nine-point circle, a famous construction with connections to other triangle geometry that we've looked at before. But first, I'd like to re-introduce the centers that we've met so far. You should imagine that they're members of a super team each with their own little sequence that the cartoon always shows when they go into action.

And imagine that they're appearing with one of these dramatic cartoon backgrounds like this. I would go ahead and do that, but it would look really messy on the little screen you're staring at. It will look better in your imagination.

Anyway, here we go. Here they are, now each with its own thematic color.

G, the Centroid!

Secret origin: intersection of the medians

Trilinear coordinates: 1/a : 1/b : 1/c

Affiliations: Euler line, isogonal conjugate of the symmedian point

Super powers: center of gravity of triangle area • center of gravity of triangle vertices • divides triangle into equal parts ABG, BCG, and ACG • divides medians 2/3 of the distance from vertex to midpoint

O, the Circumcenter!

Secret origin: intersection of the perpendicular bisectors

Trilinear coordinates: cos A : cos B : cos C

Affiliations: Euler line, isogonal conjugate of the orthocenter

Super powers: center of circumcircle • circumcircle is locus of points with degenerate pedal triangles • relates to incenter via Euler's theorem in geometry

H, the Orthocenter!

Secret origin: intersection of the altitudes

Trilinear coordinates: sec A : sec B : sec C

Affiliations: Euler line, isogonal conjugate of the circumcenter

Super powers: constitutes an orthocentric system along with the vertices • incenter of orthic triangle • sides of orthic triangle are antiparallel to sides of reference triangle • concyclic with a vertex and two adjacent feet of altitudes

I, the incenter!

Secret origin: intersection of the angle bisectors

Trilinear coordinates: 1 : 1 : 1

Affiliations: entourage of excenters

Super powers: center of the incircle • isogonally self-conjugate • forms orthocentric system along with excenters • relates to circumcenter via Euler's theorem in geometry • always lies in interior of orthocentroidal disc

K, the symmedian point!

Secret origin: intersection of the symmedians

Trilinear coordinates: a: b: c

Affiliations: isogonal conjugate of centroid

Super powers: perspector of reference and tangential triangles • parallels through K intersect sides in six concyclic points • antiparallels through K intersect sides in six concyclic points, with K at the center of the circle • circles through K and two vertices intersect sides in six concyclic points • lines joining midpoints of altitudes and sides pass through K • centroid of its own pedal triangle • just very pretty

So now that we've got the super team together, it's time to introduce them to someone new. I know, you're thinking we've got this established cast of characters, and they relate to each other in so many varied and intimate ways. How could a new triangle fit into these relationships? Wouldn't it feel like a superfluous add-on at this point in the show?

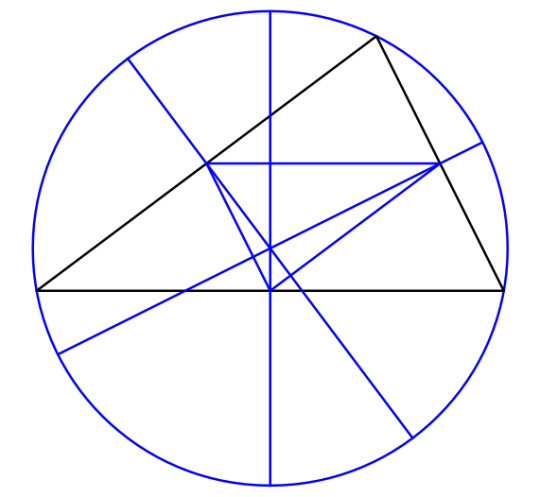
Well, let's see. Let's go back and look at the midpoints of the sides. We find the midpoints by drawing perpedicular bisectors on each side. Those lines meet at the circumcenter, which makes the midpoints the feet of the circumcenter. The triangle formed by the midpoints is the pedal triangle of the circumcenter.

Any three points also determine, naturally, a circle. The circle formed by the feet of a point is called the pedal circle of the point. And every point has a pedal circle with respect to a given triangle.

The orthocenter, for instance, has a pedal circle defined by the feet of the altitudes, and guess what? It's the same circle! What's more, this circle bisects the segments that join the orthocenter with the vertices. For this reason, the circle is called the nine-point circle, and its center is the nine-point center, N. Let's prove that it exists.

Theorem: in any triangle the midpoints of the sides, the feet of the altitudes, and the midpoints of the segments connecting the orthocenter to the vertices lie on a common circle.

Here's our triangle ABC, with midpionts of sides Ma, Mb, Mc, feet of the altitudes Ha, Hb, Hc, and midpoints of segments joining H and the vertices Sa, Sb, Sc. We will rely on the fact that a line segment joining the midpoints of two sides (a midline) is parallel to the third side and half as long.

In green we have horizongal segments MbMa, a midline of ABC, and SaSb, a midline of ABH. Both of these midlines are parallel to side AB and half its length, so they are parallel to each other and equal. Vertical green segments MbSa and MaSb are midliness of ACH and BCH respectively, so they are also parallel and equal. Therefore the green segments form a rectangle.

In the same way, the blue segments also form a rectangle. These two rectangles have a common diagonal MbSb, and so have the same circumcircle. And McHcSc is a right triangle, and its hypotenuse McSc is also a diagonal of the blue rectangle. Therefore Hc is on the same circle, and by analogous argument so are Ha and Hb.

Since now we can be sure the nine-point circle and its center exist, it should get its own introduction scene and signature color.

N, the nine-point circle!

Secret origin: pedal circle of circumcenter and orthocenter

Trilinear coordinates: cos(B-C) : cos(C-A) : cos(A-B)

Affiliations: Euler line

Super powers: passes through nine points • many many others which we will get to next

So those are some nice ways that connect the nine-point circle to the circumcenter and orthocenter. And it's cool that this new character N has some connections to the established characters O and H, but what about the other points? Can we find some connections there?

Yes, we can, because it turns out the nine-point center is connected to everything. Would you like to see some of them?

(This is me right now.)

Because there are kind of a lot.

The nine-point circle is tangent to the incircle and the excircles. If you are keeping track, that's now 13 points of interest on the nine-point circle.

The radius of the nine-point circle is half that of the circumcircle. This is easy to see, because the circle is the circumcircle of the medial triangle, which is half the size of the reference triangle.

The nine-point center lies on the Euler line midway between the circumcenter and the orthocenter. The centroid is one-third of the way from the circumcenter to the orthocenter. These positions give the orthocenter and centroid special status with regard to the nine-point circle.

The nine-point circle bisects any line segment from the orthocenter to the circumcircle, making the fact that it bisects the tops of the altitudes into a special case of a general property.

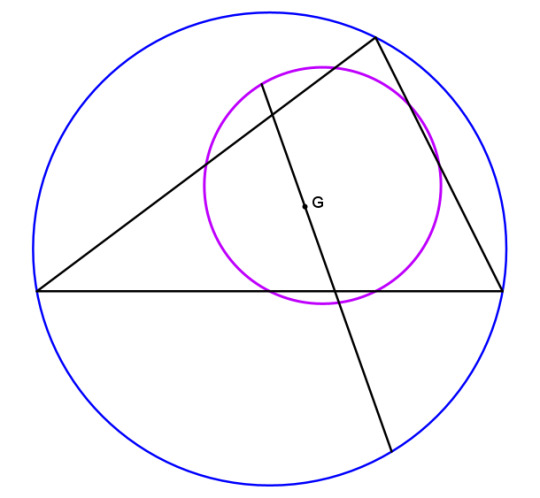
The centroid trisects any line segment extending from a point on the nine-point circle through G and on to the circumcircle. Another way of saying this is that G is a center of dilation between the circumcircle and nine-point circle with scaling factor -1/2. In triangle geometry, this particular dilation through G is called taking the complement of a point, so a third way of describing this relationship is to say that the nine-point circle is the complement of the circumcircle.

The nine-point center is also the center of gravity of A, B, C, and H.

As we have seen previously, the vertices and the orthocenter form an orthocentric system, meaning that any one of the points A, B, C, and H is the orthocenter of the other three. For all four of the triangles ABC, ABH, ACH, and BCH, the feet of the altitudes are the same, so they all share the same orthic triangle and the same nine-point circle.

But each of these four triangles has its own incircle and set of excircles, and the nine-point circle is tangent to all of them, making sixteen points of tangency. That's now 29 points of interest on the nine-point circle.

The incenter and the excenters form another orthocentric system, and the nine-point center of this system is the circumcircle of the original triangle. The reference triangle ABC is the orthic triangle of the excentral triangle JaJbJc.

And speaking of the orthic triangle, it defines three other triangles in the corners that are similar to the reference triangle. The Euler lines of these corner triangles coincide at a point on the nine-point circle. That brings us to 30 points of interest on the nine-point circle.

Let's go back to pedal triangles, and remember that if a point is on the circumcircle, its feet are colinear and its pedal triangle has collapsed to a line segment, called a Simson line. The envelope of these line segments form a shape called the Steiner deltoid.

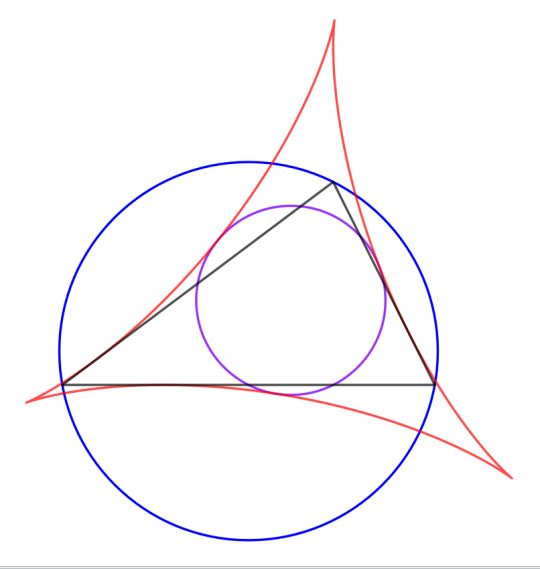
The nine-point center is also the center of the Steiner deltoid, and the circle is tangent to the deltoid at three points. There are four different circumcircles in an orthocentric system, so there are twelve points of tangency in all, so we now have 42 points of interest on the nine-piont circle.

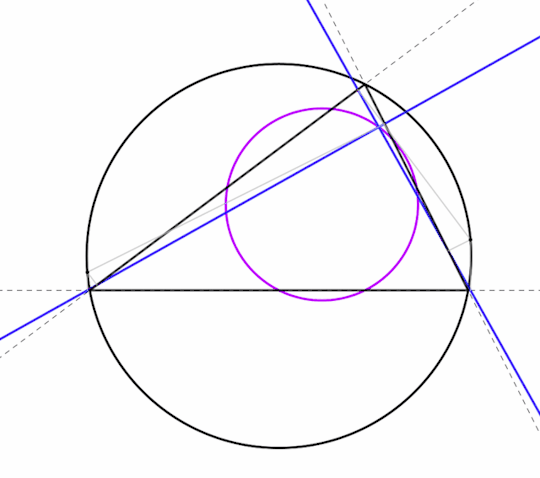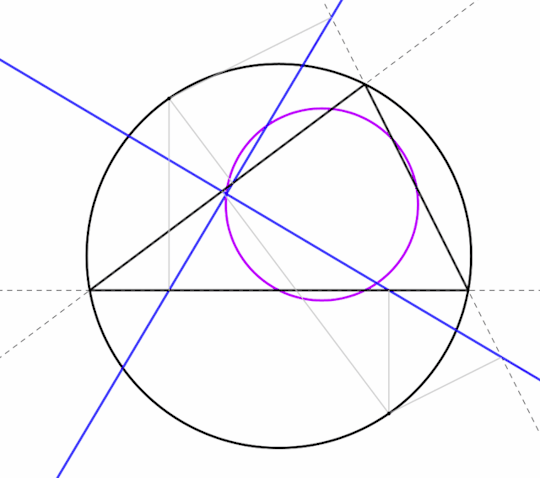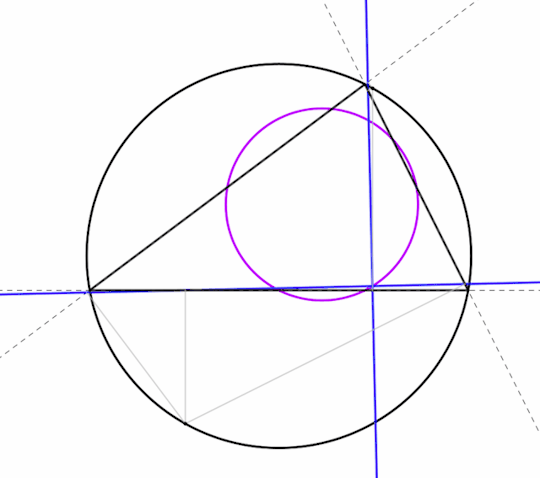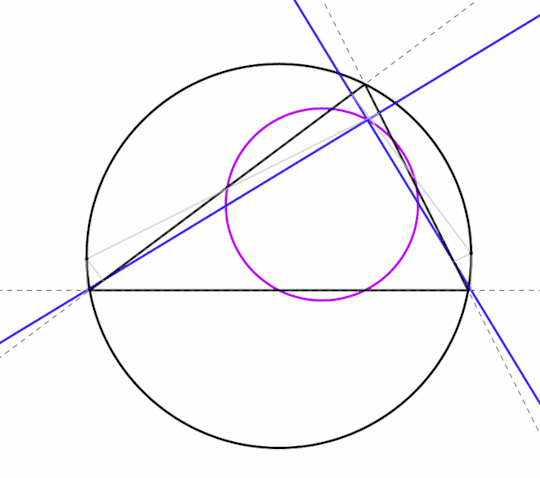
The Simson lines of two opposite points on the circumcircle intersect perpendicularly on the nine-point circle.

You may have noticed that in citing all these connections I haven't mentioned the symmedian point K so far. As far as I can tell, K is just not that very strongly connected to N. However, here's one: the circle through K, N, and O is orthogonal to the circle with diameter GH (the orthocentroidal circle). That's five members of our super team tied into one relation. But that's all I've got. Sometimes members of a team don't interact that much.

And this is the kind of thing you look for in a successful series, right? You have an established cast of characters, with a rich, dense lore linking them all together in various ways. Then, as the story develops and someone new is introduced, new retlationships make the lore even richer. That that's why I'm in the triangle fandom.

With that, I think the only question left to answer is "Hey, Square, do you happen to have a group portrait of the whole team together in one clear and not at all confusing picture?" And of course I do.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.

[squareallworthy]

Triangle Tuesday 6: More on parallels and antiparallels, wonky hexagons, and a couple of conjectures

I had a very busy weekend so I haven't been able to write up the next subject I had planned on. Instead, I'm just going to show you some neat stuff about parallels and antiparallels in a triangle and not prove any of it.

To recap, last week we saw that a special property of the symmedian point K of a triangle is that if you draw parallels to the sides through it, the points where they meet the sides lie on a circle. This is called the first Lemoine circle, and I have labeled its center as point U.

And if you draw antiparallels through K, they also all meet the sides on a circle. This is the second Lemoine circle, and its center is K.

And we can also draw circles through K and any two of the vertices. These circles intersect the extended sides at points on a common circle as well. This is a much more recent result that I learned about here, and we'll call this the third Lemoine circle, with its center at V.

What I didn't mention before is that these three points K, U, and V all lie on the same line, along with the circumcenter O.

This line that connects O and K is known as the Brocard axis. What's more, as far as I can tell, the four points are equally spaced on the Brocard axis. I haven't been able to find a reference to that, and I haven't even tried to prove the equal spacing, so we'll just call that part a conjecture.

Another line that runs through the circumcenter is the Euler line. Other famous points on this line are the centroid G and the orthocenter H.

Not so famous, but still in ways important, is the point I have labeled W, the midpoint of G and H and the center of the orthocentroidal circle. These four points O, G, W, and H are also equally spaced. And (more conjecture) the lines GU, WK, and HV are all parallel.

Again, I have not even tried to prove this, but I thought it made a curious observation and I wanted to share it.

Let's switch gears and go back to the first Lemonie circle.

The blue segments are, remember, parallel to the sides of the triangle. If we join the endpoints of these segments to their nearest neighbors on adjacent sides, we get a self-intersecting cyclic hexagon, in gray. And it turns out that the new segments we have just drawn (red) are antiparallels.

Shall we also try that with the second Lemoine circle?

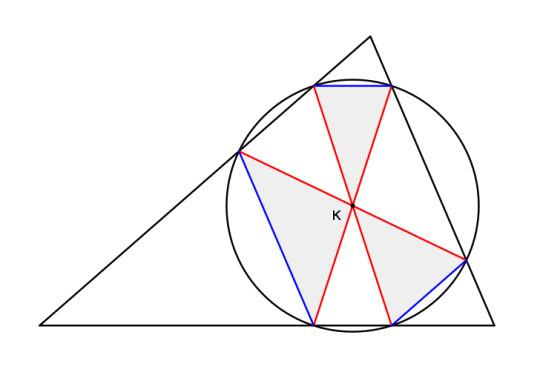
Yes, we find that the new segments we've added are parallels to the sides. So in both cases we got a self-intersecting hexagon of alternating parallel and antiparallel sides.

So is this another special property of the symmedian point?

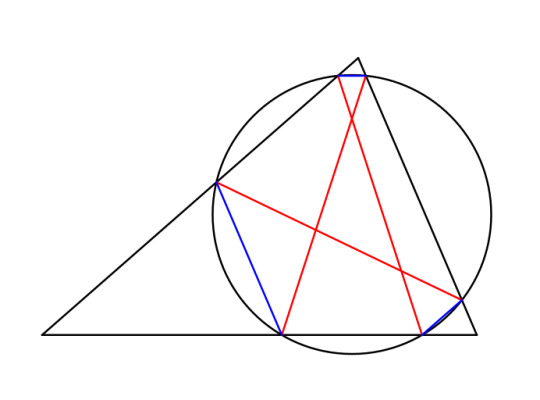
Here is a hexagon of alternating parallel and antiparallel sides that I drew starting from an arbitrary point on the bottom side of the triangle. We still get all the vertices of the hexagon landing on a circle.

And indeed this construction works if you start from any point. The symmedian point is only special in that if the three parallels or antiparallels cross at one point, that's where they do it. Hexagons like this are called Tucker hexagons, and their circumcircles are called Tucker circles.

Okay, but what if we made a hexagon like this but only using parallels?

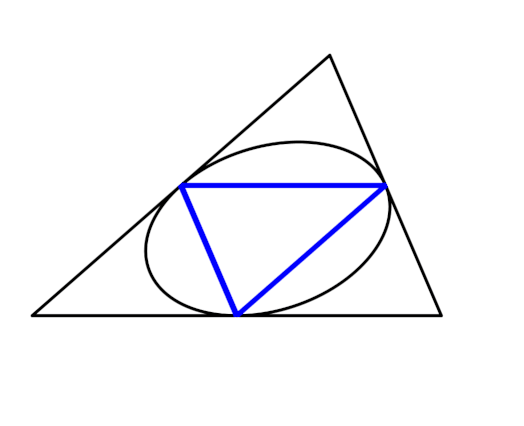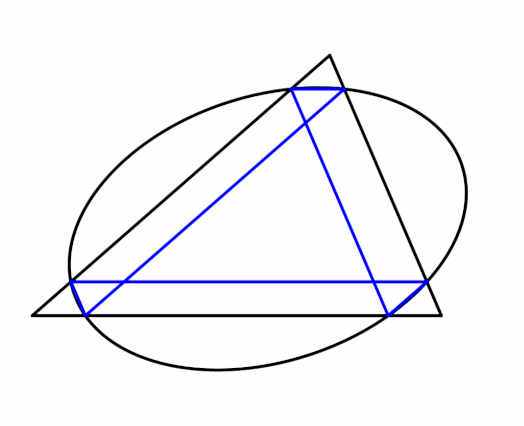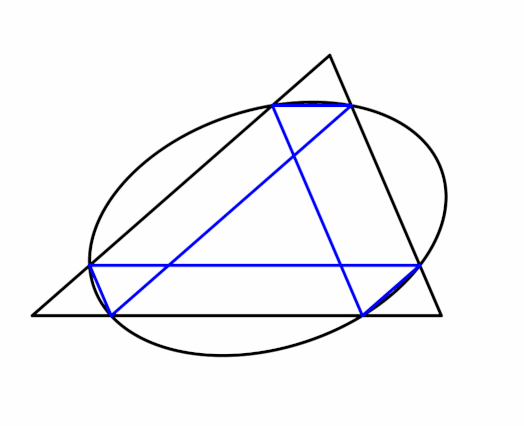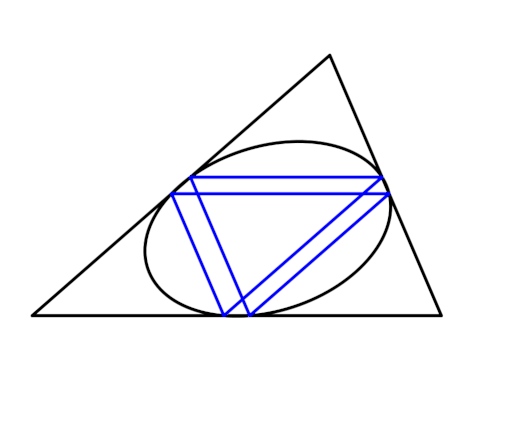
We still get a hexagon, but the points of contact with the sides fall on an ellipse rather than a circle. When three segments meet, they do so at the centroid, and when segments overlap in pairs so that we get a triangle, it's the medial triangle. This hexagon is called Thomsen's figure, btw.

What about using only antiparallels, then?

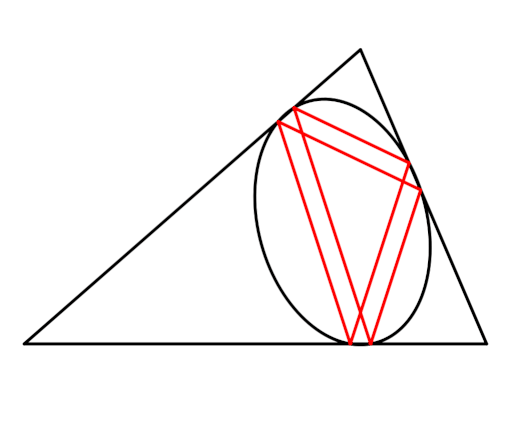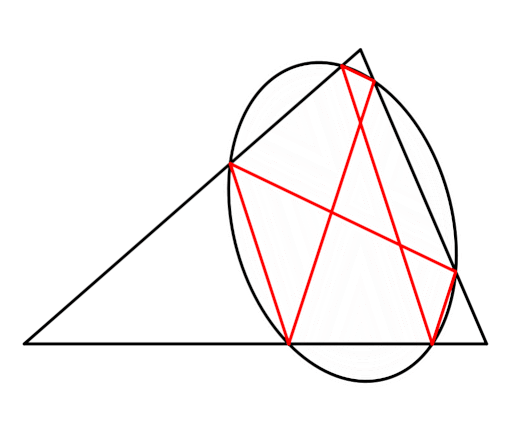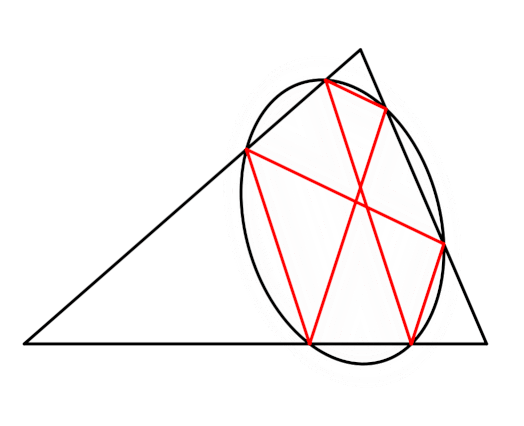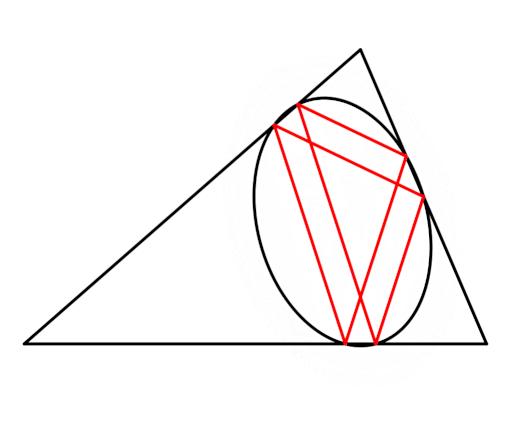
Looks like it forms an ellipse in the same way Thomsen's figure does. I have no idea what this is called, if it has a name at all. I'm just playing around and didn't even expect it to work.

That's about all I have time for this week. Hopefully this weekend won't be so busy and I'll be back with something more focused.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.