thetwomeatmeal

[thetwomeatmeal]

Any thoughts on Gardner's critique of conceptualism and Lakatos? (NY review of books - Is Mathematics Real? by Martin Gardner - sent you a link as message)

I have no idea how old this ask is, haha. I’ll have to look it later!

[thetwomeatmeal]

'those propositions which have "sense" and whose truth can thus be determined logically' Isn't this precisely backwards? Anything that can be proved in logic is a tautology, and thus without sense (4.461). Or do you mean something else by "determined logically"?

Thanks for the correction - I mean that an ordinary-language sentence is supposed to either be translatable into a sentence of the logical language, where it’ll either be found to be true or false, or not be so translatable, in which case it’s called senseless. Even in the former case, the sentence has to be checked against some empirical facts about the world, so it may not end up tautologous. I should’ve said “determined logically/empirically”.

[thetwomeatmeal]

pi|explanation

My first time around, I missed what's going on with the words "explanation" and "signification" [Erklärung and Bezeichnung], two of the more "technical" terms used in the opening of the book.

Explanation. We remember the conversation-exiting "Explanations have to come to an end somewhere" from §1. There's also a squeamishness about calling ostensive teaching of words "ostensive explanation" in §5, because "the child cannot yet ask what the name is".

Although this isn't spelled out, I think the point is that explanation is to be thought of as a language-game itself. Here's how we play: you explain something I'm confused about to me. If I'm still confused, I ask you for further explanation, "making my confusion specific" if need be, and you give it. The game ends when I'm no longer confused.

The standard for a good explanation, then, is not logical but rhetorical: it has to satisfy the other person. This could take a long time, or a short one. One doesn't "explain" using axiomatic proofs, because (a) outside of some very strange contexts like formal math, these rarely work as good explanations; (b) the other person is within their rights to be confused about the axioms. Also, one can't "explain" to a pre-linguistic child, because they're unable to participate in the game. (You can kick a soccer ball towards someone with no legs, but you are probably not playing soccer with them by doing so.)

Signification. This is discussed at length in §10, which I won't reiterate. But a set of significations, certain relations of words to concepts or objects, would be the core part of an Augustinian-style description of a language; and the metaphysics of such significations -- are they in the head? the pictures evoked in §6? how are they taught? -- form a major philosophical problem for such a description. (It scarcely needs to be said that these questions are still major problems for many philosophers today, nor that they have the pesky tendency to obstruct empirical understanding of language...)

Again, Wittgenstein wants to substitute the metaphysical role filled by signification in such theories with a rhetorical role played by sentences of the form "this word signifies that." And as with explanation, we see that such sentences primarily exist to clear up certain kinds of confusion. If you notice me consistently bringing you slabs when you've asked for pillars, you may have to tell me that "pillar" signifies a pillar, not a slab. But the preconditions for doing this are us sharing most of the language to begin with -- in this case, I have to know that the words, in general, mean orders to bring various kinds of stone. (I have to know something about how words in this language signify, in general.) Thus, at no point do you have to deliver an entire theory of meaning to me.

(It might be worth noticing that speakers of the language-games introduced in §2 and §8 have no way of having such conversations about signification -- by hypothesis, they have no terms for talking about words themselves. But to have a functioning stone-structure-building society, there has to be some way to correct errors. This is a difficulty with Wittgenstein's method: "to imagine a language is to imagine a form of life" only if one's imagined a language of sufficient expressive power... so what conclusions can we really draw from his very basic examples?)

The notion of "signification" as a common property of words in general is shown up in §13 by the fact that words are used in essentially different ways. Thus, the act of correcting me about the signification of a word takes a different shape depending on what kind of word it is (a concrete noun, or an ordinal, or a grammatical particle...), as well as what kind of confusion I actually have.

To summarize, you may have to correct me about significations of words in a language we both speak. But you should never have to explain how signification works in general in our language. You may have to explain to me concepts I'm confused about. But you should never have to explain everything to me.

But "explaining everything" is exactly what positivist grand theories like that of the Tractatus are trying to do! The words "explanation" and "signification" are introduced in this way to emphasize that such questions don't have to be asked.

The end of explanation. There is, however, a point on which the author of PI agrees with the author of the Tractatus. The Tractatus is just as aware of the problem of continually asking for further and further explanation. The point of the book is to work out an alternative solution: a hard line around those propositions which have "sense" and whose truth can thus be determined logically. Explanations can be given inside that line by logical analysis of the terms involved, and outside of that line, any questions are simply senseless (and the logical analysis will instead indicate to the questioner that they are confused).

T 6.5-6.51: "For an answer which cannot be expressed the question too cannot be expressed. ... For doubt can only exist where there is a question; a question only where there is an answer, and this only where something can be said."

In both T and PI, explanations come to an end: in one, when they transcend logical analysis; in the other, when the questioner stops being confused.

[thetwomeatmeal]

Right, so does anyone know how to turn off whatever text replacement is turning (+R+) to the symbol (R)?

[thetwomeatmeal]

Testing something out: (R) (C)

\(BGL(R)^+\)

[thetwomeatmeal]

Me & R when William Onyeabor - Good Name comes on

[thetwomeatmeal]

nearness in frequency

I was reading Spooky Action at a Distance and it pointed out that sound waves will go right through each other.

Objects will push on each other when they’re nearby, they’ll collide when they’re nearby in space. But sound waves interact when they’re nearby in frequency–I’m thinking of the “beats” that you hear when tuning a guitar. You play harmonics on two different strings which are supposed to come out as the same note. And you know you’re getting close when you hear “beats”, periodic fluctuations in volume, which slow down as you get more in tune and the frequencies get closer together. But like… it’s really astonishing when you think about it, that one sound is affecting another sound–play one string and you hear a constant volume, add a second and you hear a fluctuating volume, which can go below the original volume–the second string is preventing you from hearing the first, at regular intervals. It’s so different from normal experience, that when you hear two sounds together, it’s like hearing one sound, and another sound. And it requires nearness in frequency. Noise canceling headphones I imagine work similarly, playing something of exactly the same frequency but shifted phase–I don’t really know though, it’s not like a guitar where I can see everything happening.

[thetwomeatmeal]

Father uses sons’ drawings as inspiration for anime transformations

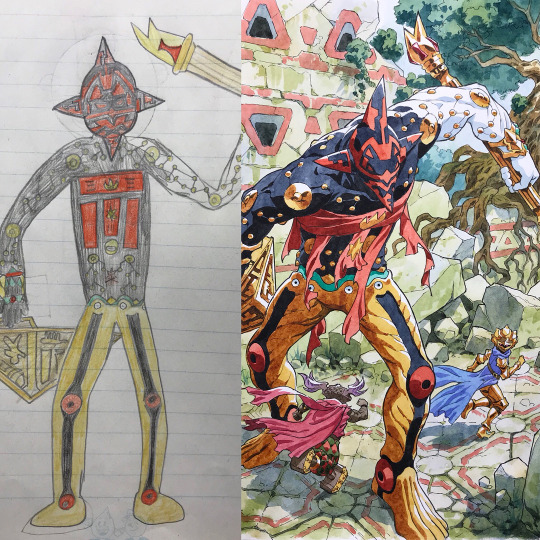
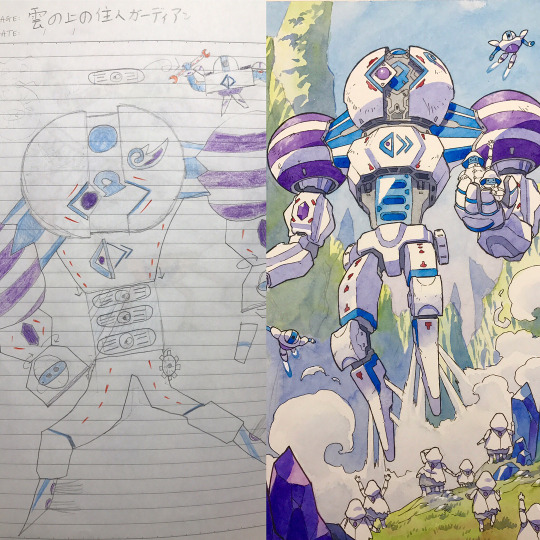
By: Thomas Romain (twitter | instagram | youtube | patreon)

[thetwomeatmeal]

The equations for the streamlines of laminar fluid flow around asolid cylinder can be solved in closed form. The equation for each streamline has a graph with another component inside the cylinder. I wonder if these have any physical significance.

[thetwomeatmeal]

An acoustics side note that didn’t make it into that post is the fact that, while I’m pretty sure that the volume of a guitar largely comes from the vibrations of the string itself, amplified by either the hollow body or electric pickups, violin strings apparently exert force on the bridge and cause the top of the violin to diaphragm back and forth with respect to the bottom. So while a plucked violin string behaves identically to a plucked guitar string, the force it exerts the bridge over time looks like a square wave, and you get a very different sound.

[thetwomeatmeal]

I’ve made a little demonstration of Fourier series that shows you how a string vibrates when plucked.

Red is the actual string: L is its length and b and h control where it’s plucked. The solid green curve gives a Fourier series approximation to it, whose precision you can adjust with M. The solid blue curve shows how that Fourier series evolves over time. The dotted green and blue curves do the same for a single term in the series -- that is, a single harmonic, which you can choose with q. k controls the wave speed.

For the uninitiated, here’s how this works. A string that’s fixed at both ends can vibrate in certain special ways called harmonics or normal modes (which are displayed on the graph as the dotted curves). In the simplest of these, q=1, the string takes the shape of a half-sine wave, which then oscillates up and down with all points on the string moving in phase. In the next simplest, q=2, the string is shaped like a whole sine wave; the midpoint of the string is perfectly stationary, and the two halves of the string oscillate in opposite directions. In the q=3 mode, three half-sine waves fit on the string, and so on.

Each of these modes oscillates with a certain characteristic frequency, and these frequencies have an elegant relationship: the frequency of mode q is q times the frequency of mode 1 (called the fundamental frequency). So if the fundamental frequency is 440 Hz, the A above middle C, then the second harmonic is 880 Hz, the third is 1320 Hz, and so on.

Now, when I pluck a string, I’m not making any of these smooth sine wave shapes, but a crude, pedestrian angle. But Fourier analysis says that we can see how the wave evolves over time -- in fact, how any initial waveform will evolve over time, no matter how complicated -- by following a simple recipe:

Write the initial waveform as a sum of normal modes.

Each normal mode in this sum then evolves independently, by oscillating at its own characteristic frequency.

At time t, you can figure out the shape of the string by calculating where each normal mode is at time t, and adding them back together.

This is exactly what you see on the graph.

So that’s the math. How about the consequences for music? First, though you can’t see it in real time, this graph shows that a plucked string actually always has a sharp corner, which moves up the string to the mirror image of the plucking point, and then shuttles back. Hermann van Helmholtz described first described this phenomenon in the more complicated case of a bowed string, where the corner traces out a lens shape as it moves.

Second, the string as a whole vibrates with the same frequency as its lowest normal mode, i.e. the fundamental frequency. But this graph makes it clear that the real vibration has some mixture of the higher harmonics. Exactly how they’re mixed determines the unique timbre of the instrument. So in a violin (with vibrating, continuously bowed strings), a trumpet (with a vibrating air column), or a clarinet (with a vibrating reed), the same principles are at play, but the actual mixture of harmonics is different, producing different sounds. (To complicate things further, the bodies of these instruments vibrate in special ways too, thus amplifying or suppressing certain modes!)

Third, by stopping the midpoint of the string from vibrating, one can silence all the odd normal modes while allowing the even ones to continue. This produces a pitch whose lowest mode is the second harmonic of the previous pitch, making it an octave higher. Stopping the string at one of its one-third points makes it sound at the frequency of the third harmonic, and so on. Guitarists call this “playing harmonics” -- you touch the string at one of these points without fretting it all the way, and produce an unusually high and clear tone. The higher of a harmonic you want to isolate, the harder this gets to do: the higher harmonics occur in the plucked-string vibration with weaker amplitudes, and the margin of error for where to touch is smaller.

Fourth, one can also do the opposite, which you can see on the graph by setting b to be an integer fraction of L. For example, if you pluck the string at its midpoint, then the second, fourth, and so on harmonics don’t sound at all. I’ve heard this is important in piano design. The hammers are supposed to hit the strings exactly 1/7 of the way along their length in order to silence the seventh harmonic, which is two octaves and a very flat minor seventh above the fundamental, so sounds dissonant to us.

Theoretically, this sort of thing is applicable to guitar or violin technique, too, though. I haven’t seen this actually used, but I have seen classical techniques where one plays close to the bridge or end of the string (sul ponticello). As you see if you make b close to L, this accentuates the higher harmonics relative to the fundamental, producing what I’d call a sharp, metallic sound. (You might also notice that the approximation gets worse as b approaches L, which is another instance of the same phenomenon: the higher terms in the series which are cut off by the approximation become more relevant.

I got into this from the happy coincidence of playing guitar and teaching Fourier analysis. Do you know things about the acoustics of other instruments, or other aspects of music production that can be mathematically modelled? I’d love to hear from you!

[thetwomeatmeal]

Pictures of some normal modes of unattached violin plates (top) and the violin itself (bottom), from the Grove Music article on “Acoustics”

[thetwomeatmeal]

“Imagine a woman in the long skirts and high collar of the early 20th century standing in front of the painting she created. It is a massive piece—about 10 feet tall by 8 feet wide—and it is not a landscape, a portrait, a still life, nor a scene from myth or history. Dominating the composition is a bold yellow form reminiscent of a plant or sea creature, glowing amid colorful, biomorphic shapes and vigorous lines. This is just one of 10 such works that she has created almost entirely alone—sometimes walking on her work as she lays down the paint—and one of 193 radically abstract paintings that she has made in a few short years, between 1906 and 1915. None of these details fit with the story told in museums and art history courses. We know the first abstract painters so well that we often refer to them by last names alone: Kandinsky, Malevich, Mondrian. We know who is celebrated for doing “action painting” on giant canvases laid on the floor—Pollock. Each of these men has been lauded for opening a way into new territory. As it turns out, that territory had already been explored by another artist. Her name was Hilma af Klint.”

— Who Was Hilma af Klint?: At the Guggenheim, Paintings by an Artist Ahead of Her Time by Caitlin Dover

[thetwomeatmeal]

you will be healed dude. touch my muscles

[thetwomeatmeal]

[thetwomeatmeal]

this bit from The Jewish War feels kind of, idk, Paul Auster:

“And here he found a perfect and unexpected solitude, while ever body avoided him, and nobody durst come at him; for he was equally hated by all men; and now that hatred had liberty to show itself, and the dread men were in at the king's anger made men keep from him; for the whole city [of Jerusalem] was filled with the rumors about Antipater, and Antipater himself was the only person who was ignorant of them; for as no man was dismissed more magnificently when he began his voyage to Rome so was no man now received back with greater ignominy.”

[thetwomeatmeal]

Indeed, the reading lists of contemporary military institutions include works from around 1968 (with a special emphasis on the writings of Deleuze, Guattari and Debord), as well as more contemporary writings on urbanism, psychology, cybernetics and postcolonial and poststructuralist theory. If writers claiming that the space for criticality has to some extent withered away in late twentieth-century capitalist culture are right, it surely seems to have found a place to flourish in the military.

Eyal Weizman, “Lethal Theory” (pdf here)