#eulers formula

[oopsallsticks]

Current Family Photo 🧡🖤🤍

I love every one so far -B

[ryanthel0ser]

I am now believing that Vincent just wrote all of his calculus notes on a wall in the basement for reference because he too was frustrated flipping through his notes like I am

[jijjmoon]

3.14 Happy pi day!

so, umm I came back earlier than I thought. I can draw if I draw at daytime. I usally drew at night but drawing at daytime is better than not drawing.

[river-gale]

STOP naming things after euler. i have nothing but respect and admiration for leonhard euler and his contributions to the beautiful field of mathematics but TOO MANY THINGS ARE NAMED AFTER HIM. please. enough. it's getting so confusing

[aedislumen]

Another question because why not..

Your favourite math equation?

I admit that there have been a lot of equations I liked so much in the past that I wanted to have them tattooed (Shroedinger's, Dirac's, Maxwell's etc).

While my fondness for them has not vanished, it's only Euler's identity that I might consider to get on my skin (I don't think I will ever do it, because I don't like the idea of having ink under my epidermis...)

Despite the name, the identity isn't present in any of Euler's works, in fact, its name derives from the fact that it comes from a special case of Euler's formula, that of x = π).

Euler's formula:

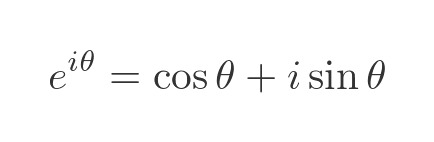
If θ = π, one gets the identity:

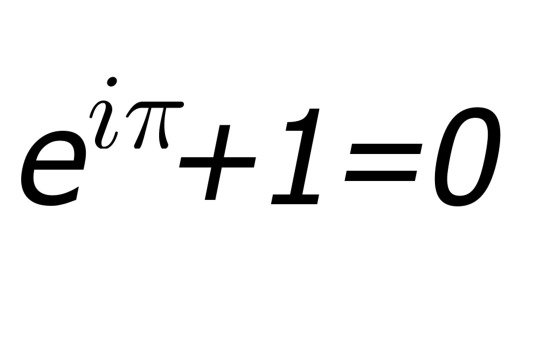
I like it a lot because it ties together the most important constants and numbers related to mathematics:

e is the Napier's constant (aka Euler's number), an irrational number, which is present in logarithm and exponential functions. It's fundamental to study growth and decrease in physical processes. it's often approximates as 2,7.

i is the imaginary unit, defined as such: i^2 = -1. Its formulation led to the introduction of imaginary numbers, that allowed some "impossible" equation to be solved. (Note that they are solvable in the domain of imaginary numbers, not in that of real ones)

π is the ratio between the circumference and the diameter. Like Napier's constant, it's an irrational one and is present pretty much everywhere, both in math and the real world.

1 is the neutral element for the operation of multiplication, meaning that any number multiplied by 1 gives back the number.

0 is the neutral element for the operation of addition: a number plus 0 gives as result that number. It's also used to define negative numbers.

[gemkun]

anonymous said : hey ratio what's your favorite mathmatical theory to ponder?

      ⸻       ❝   my   eponym   —   the   golden   ratio.   the   divine   proportion   that   approximates   to   1.618033987   ,   represented   by   Φ.   ❞   typical   ,   perhaps   even   predictable   ,   but   there   is   no   disputing   its   application   across   many   ,   if   not   all   ,   disciplines.   nor   it   being   the   pinnacle   of   aesthetic   perfection.   harmonious   in   its   simplicity.   ❝   it   is   a   notorious   theory   ,   achieving   its   recognition   as   a   unifier   of   mathematics   with   artistry.   creating   a   bridge   between   what   once   was   often   thought   to   be   dichotomous.   ❞

[blondiest]

okay kill me with a rock if i reappear here before tomorrow i'm serious

[natural-blogarithm]

i got to show proof by induction to my summer camp students today, it was very exciting

[9nid]

📘 Understanding Polar and Euler Form of Complex Numbers (JEE Focused)

Complex numbers are a fundamental part of Class 11 Mathematics and play a key role in IIT JEE preparation. After understanding the basic algebraic form of complex numbers (a + ib), we move on to more advanced forms: Polar Form and Euler Form. These are not just theoretical—JEE questions are often asked directly on them. In this article, we’ll cover both concepts deeply, in a student-friendly way,…

[edusquaremaths]

📘 Understanding Polar and Euler Form of Complex Numbers (JEE Focused)

Complex numbers are a fundamental part of Class 11 Mathematics and play a key role in IIT JEE preparation. After understanding the basic algebraic form of complex numbers (a + ib), we move on to more advanced forms: Polar Form and Euler Form. These are not just theoretical—JEE questions are often asked directly on them. In this article, we’ll cover both concepts deeply, in a student-friendly way,…

[wannadewar]

omg we've hit the point in the season for playoff math i'm about to go bury my head in the sand and scream bc isn't it worse this year since the east AND west look tight

[evenant]

Se Euler não fez, eu fiz

Eu não sei como foi que Euler inventou ou calculou $\latex e^{it}$ mas De Moivre já havia provado a sua fórmula e, como de hábito para a época, deve tê-la comunicado a outros matemáticos de renome, como Euler. Se Euler não usou a fórmula de De Moivre para definir , eu o estou fazendo aqui.

[anumberofcatschilling]

Both parts are at least somewhat related to each other. I'll clarify for any FAQ's later when I have the spoons.

Transcript:

A number of calculations for a general solution for a linear second-order differential equation with constant coefficients. The assumption here is that for coefficients a, b, and c in the differential equation, b-squared is less than 4ac, resulting in complex roots for the quadratic. The root in the upper two quadrants of the Complex Plane is used to get constant coefficients alpha and beta, and then raising e to the power of alpha plus i times beta results in two solutions that solve the differential equation because of Euler's formula. The general solution and its first derivative are written with constant coefficients C1 and C2.

Would I be rebuked for throwing the above (the general solution and its derivative) into a matrix & getting to rref for C1 and C2?

Also, I've got Autism & ADHD, and I'm aware that Autism can be more disabling than how I experience it, but the amount of control I have over my environment (complete control over the lights in my dorm & freedom to go wherever outside of class) means my ADHD is what fucks me over 75% of the time. Differences in severity aside, why do I get the impression that the general public would look at Autism + ADHD and think the Autism would be more disabling than the ADHD?

[storymaker14]

Bizzaro Right Triangles

Okay, we all know that, if you have a right triangle with sides a and b and hypotenuse c, that means a^2 + b^2 = c^2, right?

So you can have 3-4-5 right triangles, and 5-12-13, and 7-24-25, etc.

And technically, a 1-i-0 right triangle follows this pattern, too, which has made the rounds in the math meme community.

But I found something better and weirder. I found a whole family of better and weirder.

I'm gonna skip a bit of the beginning and start here:

cos x = (e^ix + e^-ix) / 2

That follows from Euler's formula; if you need a walkthrough, I can provide, but I want to start with the above. So then, it follows that:

cos (i*lnx) = (x + 1/x)/2 = (x^2 + 1)/2x

Which means that an angle of (i*lnx) radians in a right triangle will have an adjacent side of (x^2 + 1) and a hypotenuse of 2x. By Pythagoras, then, the opposite side must be (x^2 - 1)*i.

But please note: if x is odd, then the lengths of all three sides will be even, and thus can be divided by 2.

Which means -- are you holding onto your hats and shoes?!? -- means that the proportions of the right triangle with angle i*ln(3) radians... are 5-4i-3.

And for i*ln(5) radians, they are 13-12i-5.

And so forth, with all the familiar Pythagorean triplets sqrt(2n+1)-n-(n+1) showing up, just with one side imaginary and the hypotenuse and remaining side swapped -- so, (n+1)-n*i-sqrt(2n+1). They still fulfill Pythagoras, every single one.

Which I think is, pardon my directness, fucking terrific. But just as a little bonus, please note that this means the triangle with angle i*ln(2) radians, the proportions are 5-3i-4, which is just delightful IMHO.

[abiwaif]

Visualization of Euler's formula. ✍️

Euler's formula shows the deep connection between complex numbers and trigonometry. This means that when you take an exponential of a complex number, it combines circular motion (cosine and sine) with growth (the exponential function).

[askviktor]

what are your craziest most ridonkulous most astonishing hear me outs. i have a list

- the quadratic formula

- the hexcore

- the lesbian flag

- bicycle chain

- pink rhinestone cowgirl hat

- jellyfish haircut

- alternate rhyme scheme

- lady macbeth

- sheila birling

Ah, I have become familiar with this concept. You wish to know the people, objects, or concepts with which I would like to have intercourse, yes?

I am rarely sexually attracted to people, so creating such a list will prove difficult. Perhaps I will list things to which I have a deep attraction, in some form.

- The Hexcore

- Euler’s Identity

- Painlessness

- Chronomancy

- The Riemann Hypothesis

Eh, this is the best I can do.