#regular tetrahedron

[art-of-mathematics]

Quick friend-shapes needed to be made.

(meaning: I was bored and needed to do something with my hands and brain.)

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 3

Propaganda

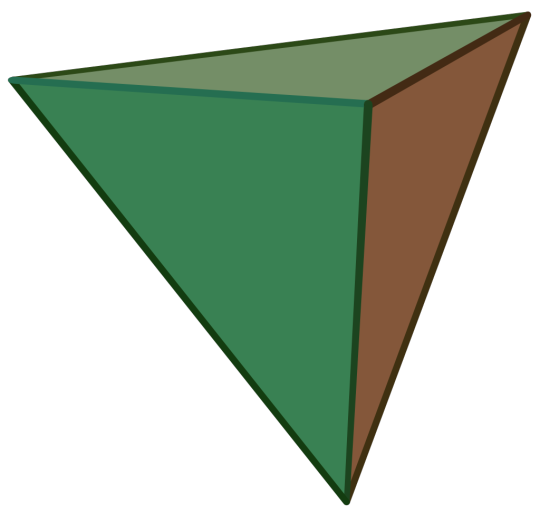
Regular Tetrahedron:

Also called the Triangular Pyramid

Platonic Solid

Regular

Dual of the Regular Tetrahedron

It has 4 regular triangular faces, 6 edges, and 4 vertices.

Self-Dual

Image Credit: Cyp

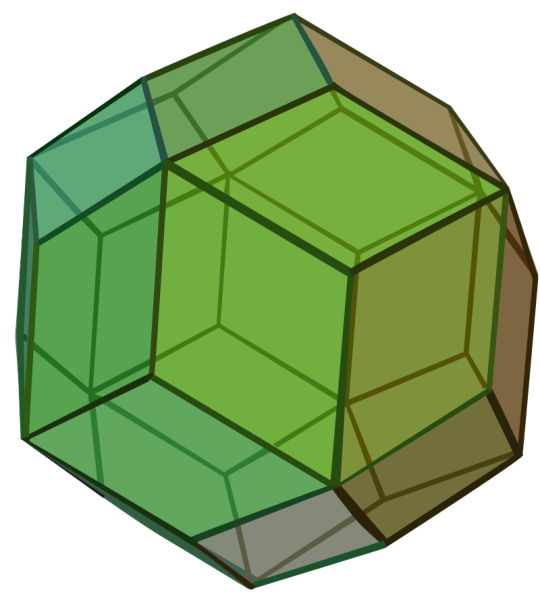
Rhombic Triacontahedron:

Also called the Triacontahedron

Catalan Solid

Dual of a quasiregular polyhedron

Dual of the Icosidodecahedron

It has 30 rhombic faces, 62 edges, and 32 vertices of two types.

One of the 9 edge-transitive convex polyhedra along with the 5 Platonic Solids, the 2 Quasiregular Convex Polyhedra, and the Rhombic Dodecahedron.

Image Credit: Maxim Razin based on Cyp

[michaelrotonal]

Here's a measure of spikiness that can be compared between dimensions.

Take some corner you'd like to find the spikiness of.

If you stand at the corner and go in a random direction (picked uniformly from the unit sphere), what is the chance you go inside the corner?

That is the pure form of the spikiness measurement. You can take its reciprocal to make the unit more usable. I'll call this unit the Spikiness of the corner.

For example, a regular hexagon's corner has a Spikiness of 3, a cube's corner has a Spikiness of 8, a tetrahedron's corner has a Spikiness of I believe around 24, and a 5D cube's corner has a Spikiness of 32.

[4denthusiast]

In This Used To Be About Dungeons, one of the gods (Garos) is the god of symmetry, and it's mentioned that there's a picture called "Portrait of 20 Symmetries" which is a religious thing, described as "intensely symmetrical", meant to be contemplated by clerics in training to bring them closer to Garos, and it just struck me as a kind of strange number of symmetries to use, assuming they're counting symmetries in-character the same way as it's usually done in real life (as the order of the symmetry group).

For one thing, that's just not very many symmetries. Even just the platonic solids have more than that. A tetrahedron has 24, a cube or octahedron has 48, and a dodecahedron or icosahedron has 120. You can depict some of the 4D regular polytopes at least somewhat clearly as a 2D picture, and a 24-cell (my favourite for multiple reasons, but partially because of its interesting symmetries) has 1152 symmetries.

The other thing is that the order (size) of a finite group has a tendency to be a number with a lot of factors. This is illustrated in all of the numbers given above. Every positive integer has at least one group with that order, the cyclic group, but more divisible numbers tend to have more groups associated with them.

The only groups with 20 elements are the cyclic group C₂₀ (the symmetries of a 20-gon with no reflectional symmetry), C₁₀ × C₂ (the symmetries of a decagonal prism where the reflections within the plane of the decagon faces are disallowed) the dihedral group D₂₀ (the symmetries of a decagon, pentagonal prism or pentagonal antiprism), and the dicyclic group Dic₂₀ and semidirect product C₅ ⋊ C₄, neither of which (I'm reasonably sure) has a geometric representation in less than 4 dimensions*. Of these, all but the last two seem pretty boring. I guess if C₂₀ is depicted in the form C₅ × C₄, then the fact that that's isomorphic to C₂₀ makes it slightly more interesting, but not much. I would guess, for this reason, that Portrait of 20 Symmetries depicts either Dic₂₀ or C₅ ⋊ C₄ somehow, with the latter being a somewhat nicer option in my opinion.

*C₅ ⋊ C₄ is a subgroup of the symmetric group S₅, which is the group of symmetries of a 4D simplex, so if you just pick some arbitrary completely unsymmetrical 4D shape and a subgroup of the symmetries of the simplex isomorphic to C₅ ⋊ C₄, and combine together the shape's 20 images under thr group, then in general you'll get a shape whose symmetry group is C₅ ⋊ C₄.

[astra-ravana]

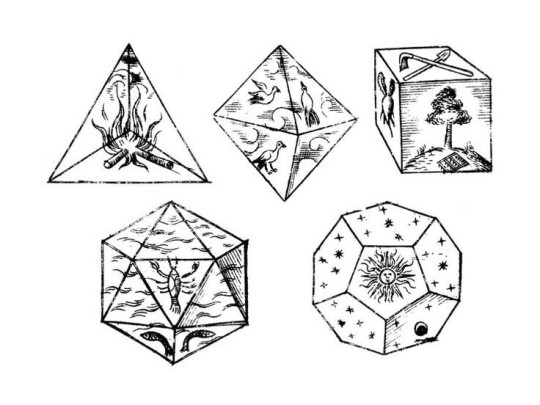
The Platonic Solids

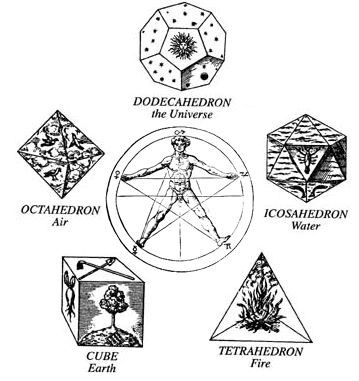
Tetrahedron, hexahedron (cube), octahedron, dodecahedron, and icosahedron-are central to sacred geometry and spiritually embody balance and symmetry. Each solid is linked to the classical elements- Earth, Air, Fire, Water, and Ether- highlighting the interconnectedness of the Universe. These shapes represent more than mere mathematical interest; they symbolize the fundamental principals that orchestrate the Universe. There are profound meanings attributed to the Platonic solids within sacred geometry and spirituality.

History And Origins

• Ancient Greece-The birthplace of the Platonic solids: The exploration of sacred geometry can be traced back to the influential mathematician Pythagoras (570-495BC). His school of thought laid the foundations for later philosophers to build upon. However, it was the renowned Greek philosopher Plato (427-347BC) who popularized the term "Platonic solids". Although he was not the first to study these shapes, his work was pivotal in their widespread recognition. In his masterpiece 'Timaeus', Plato assigned each soldid to one of the four classical elements, Fire (tetrahedron), Earth (hexahedron), Air (Octahedron), and Water (icosahedron). In later interpretations and writings the fifth Platonic solid, the dodecahedron, was associated with the element of Ether (also called Quintessence or Spirit).

• Euclid's Elements: One cannot discuss the history of Platonic solids without mentioning Euclid (~300BC), known as the Father of Geometry. His groundbreaking work 'Elements' outlined rigorous proofs for each solid shape's properties, forever cementing their place in mathematics. These expanded our knowledge of Platonic solids and helped establish a solid foundation in mathematics for future generations.

• Archimedes' Influence: Although not directly related to Platonic solids, Archimedes (~287-212BC) expanded upon their concepts by discovering thirteen semi-regular shapes known as the Archimedean solids. These are a collection of thirteen shapes which share certain characteristics with the Platonic solids. This work demonstrated that geometric principles extended beyond the five Platonic solids, further enriching our understanding of sacred geometry.

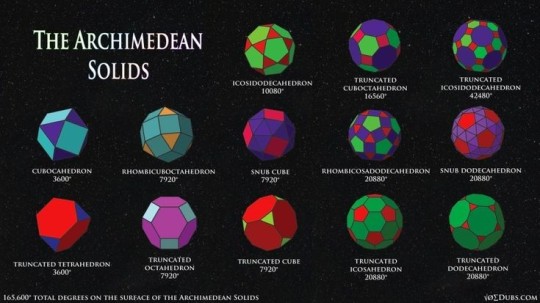
Unique Characteristics

The five Platonic solids have distinct characteristics that define them, making them the cornerstone of sacred geometry. The key defining features are:

• All faces are congruent regular polygons (equalateral triangles, squares, or pentagons).

• Each vertex (corner) connects and equal number of edges.

• They are symmetrical structures- rotation of reflection can interchange any two vertices.

These attributes result in only five possible shapes that meet these criteria: tetrahedron, hexahedron, octahedron, dodecahedron, and icosahedron. Each solid has its unique symbolism and spiritual significance that has been recognized across various cultures and ancient traditions.

The Tetrahedron

The tetrahedron, also known as a triangular pyramid, is the simplest of the Platonic solids. It represents embodying the principles of energy, passion, and transformation and the chaos of Fire.

• Geometric properties: The tetrahedron has four vertices, six edges, and four faces, all of which are equalateral triangles. It's the only Platonic solid that does not have parallel faces, giving it a sense of directionality and movement.

• Associated element: Fire

• Associated chakra: Solar Plexus

• Spiritual meaning: The tetrahedron is associated with personal power, creativity, and the drive for change. It symbolizes the dynamic and transformative nature of fire, representing the ability to purify, illuminate and transmute.

• Uses: The tetrahedron is used for focusing intentions, manifesting desires, facilitating personal transformation. It is also employed in meditation and energy work to enhance one's inner fire and to promote balance and harmony within the self.

The Hexahedron

The hexahedron, commonly known as a cube, represents the element of Earth in the Platonic solids. It symbolizes stability, solidity, and groundedness.

• Geometric properties: The hexahedron has eight vertices, twelve edges, and six faces, all of which are squares. Its equal sides and angles provide a sense of balance and symmetry.

• Associated element: Earth

• Associated chakra: Root

• Spiritual meaning: The hexahedron symbolizes stability, reliability, and the functional aspects of life. It is associated with the material world and a strong connection to to the earth.

• Uses: The hexahedron can be used for grounding, centering, and connecting to the physical realm. It is often employed in meditation to foster a sense of security and stability.

The Octahedron

The octahedron represents the element of air. It is associated with balance, communication, and intellectual pursuits.

• Geometric properties: The octahedron has six vertices, twelve edges, and eight faces, all of which are equalateral triangles. Its a dual polyhedron to the hexahedron, reflecting a balance between the physical and the mental.

• Associated element: Air

• Associated chakra: Heart, Throat

• Spiritual meaning: The octahedron symbolizes harmony, balance, and integration. It's associated with the breath of life and the floe of energy, representing mental clarity and intellectual growth.

• Uses: The octahedron is used to enhance communication, foster understanding, and promote a sense of harmony it is used in meditation to balance emotions and thoughts.

The Icosahedron

The icosahedron represents the element of Water. It symbolizes adaptability, flow, and emotional intelligence.

• Geometric properties: The icosahedron has twelve vertices, thirty edges, and twenty faces, all of which are equalateral triangles. Its many faces and edges give it a spherical appearance, suggesting fluidity and movement.

• Associated element: Water

• Associated chakra: Sacral

• Spiritual meaning: The icosahedron is associated with the flow of emotions, adaptability, and creativity. It symbolizes thr ever-changing nature of water and the ability to navigate through life's challenges with grace.

• Uses: The icosahedron is used to enhance emotional expression, activate sexuality, facilitate change, and promote connections. It's employed in meditation to connect with the fluid aspects of the self.

The Dodecahedron

The dodecahedron represents Ether, Spirit, or the Universe. It symbolizes the interconnectedness of all things and the mystery of the cosmos.

• Geometric properties: The dodecahedron has twenty vertices, thirty edges, and twelve faces, all of which are pentagons. Its complex shape suggests a connection to the divine and the unknown.

• Associated element: Ether(Spirit)

• Associated chakra: Third Eye, Crown

• Spiritual meaning: The dodecahedron is associated with the Universe, divine creation, and the interconnectedness of all beings. It symbolizes the mystery of existence and the exploring deeper levels of consciousness.

• Uses: The dodecahedron can be used to connect with the higher realms, enhance spiritual awareness, and promote a sense of unity. It is used in meditation to explore tge mysteries of the universe and the self.

[dailypolyhedra]

Polyhedron of the Day #249: Chamfered tetrahedron

The chamfered tetrahedron is a convex polyhedron. It has 10 faces (4 triangles, 6 hexagons), 24 edges, and 16 vertices. Its Bowers-style acronym is chat. It is a Goldberg polyhedron. It can be created by chamfering a regular tetrahedron or by truncating alternate vertices of a cube. Its dual is the alternate-triakis tetratetrahedron.

Image created by T. Piesk, CC BY 4.0, https://upload.wikimedia.org/wikipedia/commons/4/49/Polyhedron_chamfered_4a_edeq_max.png.

[talonabraxas]

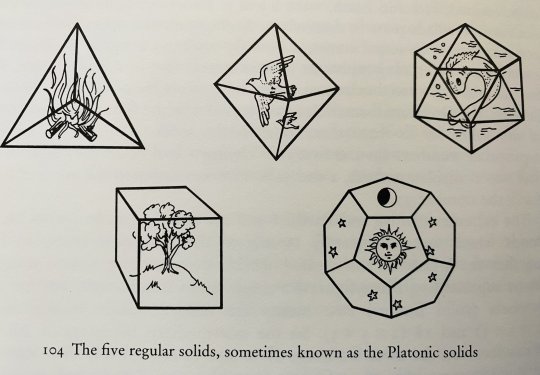
‘It is important to have a secret, a premonition of things unknown. It fills life with something impersonal, a numinosum. A man who has never experienced that has missed something important.

He must sense that he lives in a world in which in some respects is mysterious; that things happen and can be experienced which remain inexplicable; that not everything which happens can be anticipated. The unexpected and the incredible belong in this world. Only then is life whole. For me the world has from the beginning been infinite and ungraspable’. -Carl Jung, Memories, Dreams, Reflections

Portal to the Infinite Talon Abraxas The PLATONIC SOLIDS are recorded by Plato, in the Timaeus c. 360 B.C. in which he associated each of the four classical elements (earth, air, water, and fire) with a regular solid. Earth was associated with the cube (6 faces) , air with the octahedron (8 faces), water with the icosahedron (20 faces), and fire with the tetrahedron (4 faces). With the fifth Platonic solid, the dodecahedron (12 faces), Plato remarks: “…the god used it for arranging the constellations on the whole heaven".

[httpsoftbunni]

✧ What Are the Platonic Solids?

The Foundations of Sacred Geometry

Platonic Solids are among the most revered and significant shapes. These five perfect polyhedra not only serve as the building blocks for understanding the geometric framework of the universe but also embody deep metaphysical principles that link the material and spiritual worlds. Known to philosophers, mathematicians, and mystics alike, these solids symbolize a profound connection between form, function, and the very fabric of existence.

What are the Platonic Solids?

A Platonic Solid is a three-dimensional shape that exhibits two defining characteristics:

Identical Faces: All faces of the shape are congruent, regular polygons.

Identical Angles and Edges: All the edges and angles of the polygons are equal.

In addition to this geometrical perfection, Platonic Solids share the remarkable trait that the same number of faces meet at each vertex. The harmony between these properties makes them unique, and only five solids meet these criteria. These five solids are:

Tetrahedron – 4 triangular faces

Cube (Hexahedron) – 6 square faces

Octahedron – 8 triangular faces

Dodecahedron – 12 pentagonal faces

Icosahedron – 20 triangular faces

The Role of the Platonic Solids in the Cosmos

These solids are not only geometrically important but were also infused with profound symbolism by ancient thinkers. The most significant influence comes from Plato, the Greek philosopher who first associated these shapes with the classical elements of Earth, Water, Air, Fire, and Aether. In his dialogue Timaeus, Plato posits that the elements of the physical world are composed of these perfect shapes, each associated with a different fundamental force or substance. Plato’s integration of geometry and cosmology would have far-reaching effects on subsequent philosophical and spiritual systems.

The Platonic Solids and their elemental associations are:

Tetrahedron – Fire

Cube (Hexahedron) – Earth

Octahedron – Air

Dodecahedron – Aether (Spirit)

Icosahedron – Water

Plato believed that these shapes represented the foundational substances from which all physical reality is derived. According to him, the Tetrahedron’s sharp edges were suited to represent Fire, the Cube’s stability mirrored the solid, grounded nature of Earth, and the Icosahedron’s fluidity corresponded to Water. The Octahedron, with its balanced symmetry, represented the breath of life, Air, while the Dodecahedron, with its celestial geometry, symbolized the etheric substance that filled the heavens.

Beyond Plato: The Platonic Solids in Ancient Mysticism

While Plato may have first outlined the connections between the Platonic Solids and the elements, the belief in their metaphysical properties goes back much further. The Pythagoreans, a religious and philosophical school that preceded Plato, already recognized the mystical importance of geometry and numbers in the divine order. The Pythagoreans believed that mathematics and geometry were not just tools for understanding the physical world but were the very means by which the cosmos expressed harmony and order.

The Platonic Solids also had an important role in alchemy, theosophy, and other esoteric systems. Alchemists used these shapes in their pursuit of transmutation and spiritual transformation, believing that by understanding the geometry of the elements, they could unlock hidden truths about the soul and the universe. For example, the Dodecahedron, often referred to as the "heavenly" shape, was associated with the fifth element—the Aether—and was believed to be the shape that structured the cosmos. It was the geometric representation of the heavens themselves, the divine ether from which all things emanated.

In the context of Kabbalah, the Platonic Solids are also integrated into the teachings of sacred geometry. The Tree of Life, which serves as the primary symbol in Kabbalistic teachings, can be thought of as a geometric model composed of spheres, lines, and, notably, polyhedral shapes that mirror the Platonic Solids. These solids reflect the interaction between the spiritual and material worlds, with each solid representing a particular level of consciousness or divine emanation.

The Platonic Solids as "Sacred" Geometry

The term Sacred Geometry refers to the use of geometric shapes and proportions to symbolize spiritual truths. The Platonic Solids are considered "sacred" because of their mathematical perfection and their association with cosmic principles. In a world full of imperfect, irregular forms, the Platonic Solids stand as idealized representations of divine order.

These shapes are also seen as fundamental archetypes that govern the physical and metaphysical realms. The belief that all matter and energy are derived from geometric patterns or forms is deeply rooted in many mystical and philosophical traditions. Modern-day spiritual practitioners continue to use the Platonic Solids in meditation, visualizations, and other metaphysical practices to align with divine proportions and cultivate harmony.

Why Are These Shapes So Important?

The symmetry and mathematical precision of the Platonic Solids point to an underlying principle of cosmic order. They represent the divine blueprint that structures the universe, offering a glimpse into how geometry reflects the divine laws that govern creation. The fact that these shapes are perfectly balanced—with equal faces, edges, and angles—symbolizes harmony and unity.

Moreover, each Platonic Solid corresponds to different aspects of human experience. For example, the Cube reflects the grounded and material aspects of existence, while the Icosahedron reflects the fluidity and adaptability of the emotional world. The Dodecahedron, as the most complex and spiritually significant, represents the connection between the physical and spiritual realms.

By studying the Platonic Solids, one begins to understand how the physical world and spiritual principles intertwine, making them essential for anyone interested in sacred geometry and its relationship to universal laws.

[knotty-et-al]

New challenge (to establish a daily routine): Creating one new polytope info card after breakfast - each day.

(That is the first page of the list of the polytopes I want to make. (92 Johnson solids will be very very much, and I have to stop myself from thinking about those many solids. but eeeh. we might approach it step by step... )

So, I started the polytope cards project some time in the summer of this year.

I already made all 5 platonic solids,

some regular 4-polytopes (the 4D platonic solids plus the 24-cell that has no 3D sibling),

and the first 4 archimedian solids.

Today I created the truncated octahedron card:

Yesterday I made the truncated tetrahedron card:

- - -- ---

The general template of the cards is as following:

This project is still in progress.

Furtherly I want to add:

General explanations/index cards/summaries

[mbody108]

Vitruvian man

The basis of Leonardo Vinci painting gives the #geometry of man ... The five Platonic Solids have been known to us for thousands of years. These five special polyhedra are the tetrahedron, the #cube, the octahedron, the icosahedron, and the dodecahedron.

You might be surprised to find out that they are the only convex, regular polyhedra. The Greek philosopher Plato, who was born around 430 B.C., wrote about these five solids in a work called Timaeus. Historical accounts vary a little, but it is usually agreed that the solids themselves were discovered by the early Pythagoreans, perhaps by 450 B.C. There is evidence that the Egyptians knew about at least three of the solids; their work influenced the Pythagoreans. In any case, Plato mentioned these solids in writing, and it was he who identified the solids with the elements commonly believed to make up all matter in the universe. In Plato's times, people believed that all things were made up of five different atoms. They were fire, air, water, earth, with the fifth being the cosmos (the universe itself).

Plato identified fire atoms with the tetrahedron, earth atoms with the cube, air atoms with the octahedron, water atoms with the icosahedron, and the cosmos atoms with the dodecahedron. These five elements can be seen in many religions and cultures . The energy structures which I referred in the 64 condons of life blog thus got converted into point line plane cube circle numbers semiotics language and forms . The physics , chemistry , mathematics , biology, metaphysics and all sciences that we know today got embedded in the fabric of life. And then started the drama of life which we stage each day to celebrate our creation. Most people who r not aware of this wisdom live a life full of drama .

[best-shapes]

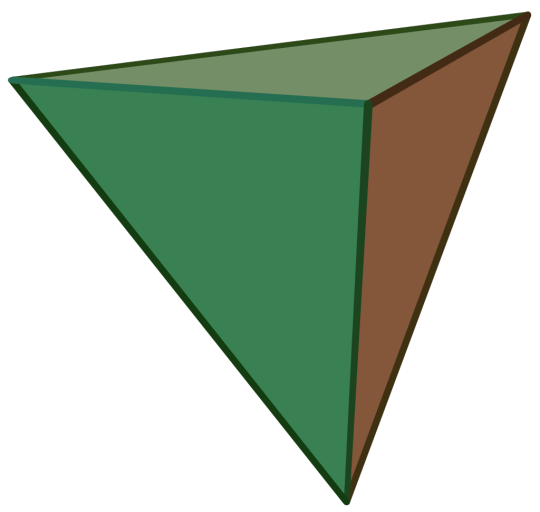
Regular-ish Convex Polyhedra Bracket — Round 2

Propaganda

Regular Tetrahedron:

Also called the Triangular Pyramid

Platonic Solid

Regular

Dual of the Regular Tetrahedron

It has 4 regular triangular faces, 6 edges, and 4 vertices.

Self-Dual

Image Credit: Cyp

Pentagonal Icositetrahedron:

Also called the Pentagonal Icosikaitetrahedron

Catalan Solid

Dual of the Snub Cube

It has 24 irregular pentagonal faces, 60 edges, and 38 vertices of three types.

Chiral so it has two forms that are mirror images of each other.

Image Credit: Cyp

[co-xeter-group]

what's the siney graph in your header?

I encourage anyone reading this to read as much or as little as they want. I hope that anyone can understand the detailed explanation, and that most math undergrads can understand most of the observations I make. The generalisations might not be so accessible all the time.

To put it tersely, its the projection of the barycentric subdivision of a tetrahedron onto the 2-sphere, visualised on a rectangle via the mercator projection.

This is closely related to Coxeter groups, the classification of polytopes, the classification of straight line Coxeter groups, the classification of regular tilings of surfaces of constant curvature, and Schl\"afli symbols.

A more detailed explanation:

Imagine taking a tetrahedron, putting a dot on the middle of each vertex, edge, and face, and connecting them all up with straight lines along its surface. This is the so called "barycentric subdivision". Then consider the origin to be in the middle of the tetrahedron, and then project the tetrahedron (and the lines we drew on it) onto a sphere. We use the mercator projection to view it like a map, but we still think of it as lying on the sphere (see below mp4 of said sphere with the barycentric subdivision drawn on it). Each face of the tetrahedron could be imagined to be coloured a certain colour, so v_2 in the diagram on my header is the vertex at the centre of the yellow face, v_1 is the vertex in the centre of one of the yellow faces edges, and similarly for v_0. These appear to be connected by curved lines, but these are straight lines on the surface of the sphere.

Assume the tetrahedron and sphere are embedded in R^3 and share a common centre at the origin.

Some interesting observations:

each of these lines we drew now gets turned into a great circle, which corresponds to a plane going through the origin

reflections in these great circles preserves the lines we drew, and correspond to automorphisms of the tetrahedron

each triangle in the subdivision has angles pi/3 radians, pi/3 radians, and pi/2 radians.

the symmetry group of the tetrahedron is S_4, where the adjacent transpositions correspond to permutations of the faces (or if you like, vertices)

the symmetric group S_4 has a presentation , where the s_i are adjacent transpositions of 4-tuples

The exponents of the (s_is_j) terms above exactly match the denominators of the angles of the triangle mentioned above

we can pick one triangle on the sphere and consider the reflections in (the faces corresponding to) its edges, denoted s_0, s_1, and s_2. These reflections permute the coloured faces of the tetrahedron, or if you like, its vertices.

we can repeatedly apply these reflections to flip across an edge or vertex of the yellow face, rotate about the centre of the yellow face (e.g. s_0 s_1), and transpose the yellow face with any other face

In this manner we can represent every symmetry of the barycentric subdivision, and by extension, the tetrahedron, in terms of these three reflections. If you don't see this, consider the effect of conjugation.

The sphere is a surface of constant curvature

This tiling generated by the tetrahedron is a regular tiling of the sphere

In short, the tetrahedron has a symmetry group S_4 (often called A_4 in analogy with the Dynkin Diagram) that has a presentation in terms of three reflections, which act transitively on this barycentric subdivision. The angles of the barycentric subdivision correspond to the relations of the presentation. One can generalise this observation and use it to classify polyhedra.

Some theoretical results.

A Coxeter group is a group W accompanied by a set of generators S = {s_1, s_2, ..., s_n} \subseteq W, such that W = <s_i | (s_is_j)^m(i,j) = 1>, where m(i,j) is an integer at least 1, m(i,i) = 1, and m(i,j) > 1 if i != j. These relations turn out to exactly correspond to the relations necessary to define a finite system of reflections in (n+1)-dimensional space.

By polytope, I mean a bounded convex polytope.

The regular tilings of the sphere correspond to regular polytopes, which correspond to the finite irreducible Coxeter groups whose Dynkin diagrams have straight lines

We can define a polytope to be regular if the automorphism group of the polytope acts transitively on the regions of the barycentric subdivision (or equivalently, its "flags"), which corresponds to chains of i-faces of the polytope ordered by inclusion

To go from a polytope to its Coxeter group, you take its automorphism group to get the group structure, and do a similar thing to above to find the generators, you arrange some hyperplanes so that their reflections satisfy the relations of the Coxeter group, generate a system of hyperplanes closed under reflection, and intersect this with an (n-1)-sphere to get the barycentric subdivision, from which you can recover a polytope and its dual polytope, which have isomorphic Coxeter groups

The regular tilings of the plane correspond to the affine irreducible Coxeter groups with straight line Dynkin diagrams.

One can study the regular tilings of hyperbolic space and classify those Coxeter groups too.

The E_8 lattice, which gives solution to 8-dimensional sphere packing has a a load of other interesting properties, corresponds to the Coxeter group E_8, via a certain semiregular polytope which is the convex hull of some lattice points.

The classification of regular (n-dimensional) polytopes and regular tilings of R^n is via the classification of Coxeter groups (and by extension Dynkin diagrams with certain properties)

There is an elegant classification according to Bourbaki that resembles the typical intuitive classification of regular polyhedra and regular tilings of R^2

Fun extensions

There are a lot of ways to represent a symmetry of a polytope/element of a Coxeter group in terms of the reflections/generators s_i. Is there an easy way to determine whether your representation of the symmetry/group element is the shortest? Yes! In fact, you can construct a DFA on the generators in the finite case.

The Cayley graph of a Coxeter group is Hamiltonian

My pfp shows the duality between an octahedron and a cube. If you draw a vertex at the centre of each face of the cube, and take the convex hull of the vertices, you get an octahedron. Note that vertices of the octahedron correspond to faces of the cube, edges of the octahedron correspond to edges of the cube, and faces of the octahedron correspond to vertices of the cube. Two vertices of the octahedron are incident with each other when the corresponding faces of the cube share an edge, and so on. To put it formally, the poset of i-faces of the octahedron and the poset of i-faces of the cube, both under inclusion, have an anti-isomorphism between them. This causes them to have isomorphic symmetry groups.

The cube has its Coxeter group with relations (s_0s_1)^4 = (s_1s_2)^3 = (s_0s_2)^2 = s_i^2 = 1. Note that here the 4 and 3 are different numbers, and the cube has a dual of an octahedron. In the case of the tetrahedron, the exponents are the same, and the tetrahedron is self dual. In general, finite irreducible Coxeter groups with straight line Dynkin diagrams correspond to self dual polytopes exactly when their Dynkin diagrams are "reversible".

This is heavily related to how the cube and octahedron have reversed Schl\"afli symbols.

[dailypolyhedra]

Polyhedron of the Day #200: Petrial cube

The Petrial cube is a regular skew polyhedron. It has 4 faces (all skew hexagons), 12 edges, and 8 vertices. It can be given Schläfli symbol {4,3}^π. It is the Petrie dual of the cube. Its Euler characteristic is 0. Its vertex figure is a triangle. Rectification of this polyhedron produces the octahemioctahedron. It is abstractly equivalent to the blended tetrahedron. Its dual is a double cover of the tetrahedron.

GIF created by A2569875, CC BY-SA 4.0, https://upload.wikimedia.org/wikipedia/commons/c/ce/Petrial_cube.gif.

Image created by Tomruen, CC BY-SA 4.0, https://upload.wikimedia.org/wikipedia/commons/a/ae/Cube_4_petrie_polygons.png.

[longformeditions]

LE063 Clarice Jensen Platonic Solids 1 14.10.2020

Clarice Jensen is a composer and cellist based in Brooklyn, NYC who graduated with an MA from the Juilliard School. In her role as the artistic director of ACME (the American Contemporary Music Ensemble), she has helped bring to life some of the most revered works of modern classical music, including pieces by Philip Glass, Steve Reich, Terry Riley, Gavin Bryars, and more.

As a solo artist, Clarice has developed a distinctive compositional approach, improvising and layering her cello through shifting loops and a chain of electronic effects to open out and explore a series of rich, drone-based sound fields. Pulsing, visceral and full of color, her work is deeply immersive, marked by a wonderful sense of restraint and an almost hallucinatory clarity. Meditative yet with a sculptural sharpness and rigour that sets it apart from the swathe of New Age/DIY droners, she has forged a very elegant and precise vision.

Her music has been described by Self-Titled as “heavily processed, incredibly powerful neo-classical pieces that seem to come straight from another astral plane”; by Boomkat as “languorously void-touching ideas, scaling and sustaining a sublime tension”; whilst Bandcamp remarked upon “a kaleidoscope of pulsing movement rich in acoustic beating and charged with other psychoacoustic effects, constantly shifting in density and viscous timbre”.

Artist notes: After reading about architect Anne Tyng and her work, I became interested in the platonic solids, the five polyhedra for which each face is the same regular polygon, and the same number of polygons meet at each corner. Plato wrote about these and assigned each with an element: earth, air, fire, water and ether (quintessence). I’ve begun using these shapes to create graphic scores, and for this piece, I placed them in the following order: Icosahedron (water); Dodecahedron (quintessence); Icosahedron + Dodecahedron; Cube (earth); Octahedron (air); Cube + Octahedron; Tetrahedron (fire).

I sought to portray sound that evokes stasis and movement at the same time, and very generally, to explore the perception of sound through dimensional space and time.

I’m fascinated by what happens to my perception of time when I’m listening to music, particularly work that is minimal and long, whether it be rhythmically active or still and duration-based. My regular and deeply embedded sense of rhythm and time is replaced by complete absence, and when I’m brought back to regular rhythm (when the piece is finished), it feels like both (or neither) an eternity and a brief moment have passed. As well, when listening this way, through repetition or duration, the details of sounds become very large, changes in sound are monumental; I find myself getting lost in galaxies inside the minutiae of something my ear has attached to. What begins as a passive and placid listening experience becomes a quite dramatic and multifaceted journey. Listening to the same piece again yields a different experience.

[bisexualisopod]

the fact that only 3 regular polygons can tile the plane is so stupid but you know whats worse? the ONLY platonic solid that can tile 3d space is the cube!! the fucking cube?? that little bitch is the only fucker that can tile 3d space?? not the icosahedron or the dodecahedron or even the god damn tetrahedron??? like what the hell is this bullshit favoratism he does not deserve that

any other lesbians on here feel like its a little messed up that the regular octagon cant tile the plane