i-research-so-you-dont-have-to

[i-research-so-you-dont-have-to]

Thank you for letting me know, have a great day!

On Four Dimensional Space

While many people think that H.G. Well's time machine was a good representation of something that could move through a fourth dimension, there is a better example: A shrink ray/growth ray.

(Explanation under the cut)

Have you ever seen this shape?

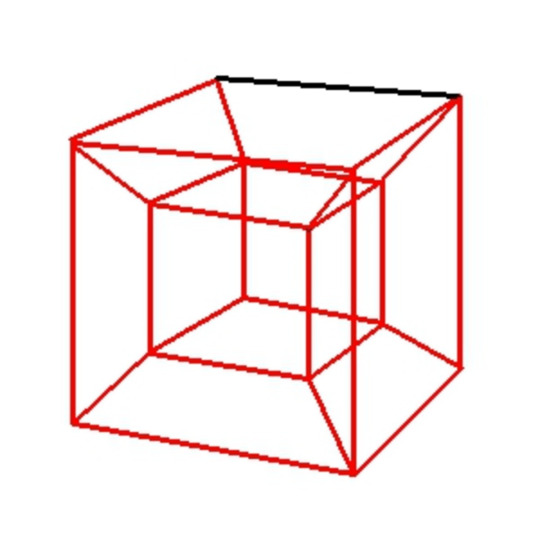
It's often called a 4-D cube, otherwise known as a tesseract, and for the longest time, I didn't understand how a cube inside a cube equaled another dimension. But I finally realized, the cube that appears smaller is actually the outside.

Let me explain. But first, I want you to imagine that you are a 2-D entity. You want to know how a square could possibly have three dimensions. You picture a square, and it looks like this:

Now, as a three dimensional being, we know that in order to make it a cube, each square is extended outward along the square by the length of one side. The problem with that is in 2-D space, you cannot have a cube. But conceptually speaking, we are aware that a cube is simply a square face that has been stretched out by the same amount as the length of one side. Altogether, it looks like this:

So, I want you to try something. Picture a square. It is 4x4. Now, without rotating it in your mind, think about that square becoming a cube. In order to do that, you either push it back by 4 squares, or bring it forward by 4 squares. The back of the cube appears to be smaller, right?

It's the same thing with going to 4-D from 3-D. For us, if you had a 4-D box with one open face, it would seem like space itself was folded into the box. So if you had a 4x4x4x4 inch box, it would appear as a 4x4x4 inch box, but it would be able to hold the same amount of items as a box with a volume of 256 inches. Each cube would have a total of 4 cubes occupying what would appear in our dimension to be the same space, but in a fourth dimension, it would be expanded out.

Now, imagine you have a paper circle and a box. You are looking down into the box, and you are holding the circle towards the top of the box. As you move the circle closer to the bottom of the box, it appears to get smaller because it is further away. The same thing would happen as you moved something through 4-D space. If you took a marble and pushed it away from yourself, it would appear to get smaller, as it would be farther away. To bring an object in a fourth dimension closer, it would appear bigger, as it would be closer. The difference is, since we cannot perceive or interact with the 4th dimension the way we can with the second or third dimension, it would genuinely be bigger or smaller for us.

A good way to demonstrate this was illustrated by Charles Hinton.

"from the perspective of the two-dimensional being, a three- dimensional sphere pushed through a two-dimensional plane would appear as a point when the sphere touched the plane, grow into a circle with the same radius as the sphere, then shrink back into a point."

The same would happen with a 4-D object in 3-D space. A sphere would begin at its smallest possible size and grow to its largest size, then shrink back down to nothing. Thus, if a 3-D object were pushed through 4-D space, the same thing would happen: If it were to be moved 'closer', it would be bigger, and if it were to be moved 'away', it would be smaller.

Sites:

https://analyticphysics.com/Higher%20Dimensions/The%20Visual%20Appearance%20of%20Higher-Dimensional%20Objects.htm

TL;DR: a shrink ray is the closest thing humans have imagined to a device that can move through the 4th dimension

[i-research-so-you-dont-have-to]

Exactly! Sorry if my wording was confusing, is there any way I could clarify it so that I don't confuse anyone else?

On Four Dimensional Space

While many people think that H.G. Well's time machine was a good representation of something that could move through a fourth dimension, there is a better example: A shrink ray/growth ray.

(Explanation under the cut)

Have you ever seen this shape?

It's often called a 4-D cube, otherwise known as a tesseract, and for the longest time, I didn't understand how a cube inside a cube equaled another dimension. But I finally realized, the cube that appears smaller is actually the outside.

Let me explain. But first, I want you to imagine that you are a 2-D entity. You want to know how a square could possibly have three dimensions. You picture a square, and it looks like this:

Now, as a three dimensional being, we know that in order to make it a cube, each square is extended outward along the square by the length of one side. The problem with that is in 2-D space, you cannot have a cube. But conceptually speaking, we are aware that a cube is simply a square face that has been stretched out by the same amount as the length of one side. Altogether, it looks like this:

So, I want you to try something. Picture a square. It is 4x4. Now, without rotating it in your mind, think about that square becoming a cube. In order to do that, you either push it back by 4 squares, or bring it forward by 4 squares. The back of the cube appears to be smaller, right?

It's the same thing with going to 4-D from 3-D. For us, if you had a 4-D box with one open face, it would seem like space itself was folded into the box. So if you had a 4x4x4x4 inch box, it would appear as a 4x4x4 inch box, but it would be able to hold the same amount of items as a box with a volume of 256 inches. Each cube would have a total of 4 cubes occupying what would appear in our dimension to be the same space, but in a fourth dimension, it would be expanded out.

Now, imagine you have a paper circle and a box. You are looking down into the box, and you are holding the circle towards the top of the box. As you move the circle closer to the bottom of the box, it appears to get smaller because it is further away. The same thing would happen as you moved something through 4-D space. If you took a marble and pushed it away from yourself, it would appear to get smaller, as it would be farther away. To bring an object in a fourth dimension closer, it would appear bigger, as it would be closer. The difference is, since we cannot perceive or interact with the 4th dimension the way we can with the second or third dimension, it would genuinely be bigger or smaller for us.

A good way to demonstrate this was illustrated by Charles Hinton.

"from the perspective of the two-dimensional being, a three- dimensional sphere pushed through a two-dimensional plane would appear as a point when the sphere touched the plane, grow into a circle with the same radius as the sphere, then shrink back into a point."

The same would happen with a 4-D object in 3-D space. A sphere would begin at its smallest possible size and grow to its largest size, then shrink back down to nothing. Thus, if a 3-D object were pushed through 4-D space, the same thing would happen: If it were to be moved 'closer', it would be bigger, and if it were to be moved 'away', it would be smaller.

Sites:

https://analyticphysics.com/Higher%20Dimensions/The%20Visual%20Appearance%20of%20Higher-Dimensional%20Objects.htm

TL;DR: a shrink ray is the closest thing humans have imagined to a device that can move through the 4th dimension

[i-research-so-you-dont-have-to]

I cited the primary source which has graphics if you need help. Did you read the whole post? We physically cannot perceive a fourth dimension; only how an object changes over time as it crosses through our dimensions. In addition, the original post was referring specifically to a 3D object moving through a 4th dimension. If you need more help, look up Charles Hinton's explanation, because it seems to me that you are not understanding the post; the tl;dr is intended to oversimplify the entirety in case the premise was interesting but reading it was too time consuming, not explain the entire concept.

On Four Dimensional Space

While many people think that H.G. Well's time machine was a good representation of something that could move through a fourth dimension, there is a better example: A shrink ray/growth ray.

(Explanation under the cut)

Have you ever seen this shape?

It's often called a 4-D cube, otherwise known as a tesseract, and for the longest time, I didn't understand how a cube inside a cube equaled another dimension. But I finally realized, the cube that appears smaller is actually the outside.

Let me explain. But first, I want you to imagine that you are a 2-D entity. You want to know how a square could possibly have three dimensions. You picture a square, and it looks like this:

Now, as a three dimensional being, we know that in order to make it a cube, each square is extended outward along the square by the length of one side. The problem with that is in 2-D space, you cannot have a cube. But conceptually speaking, we are aware that a cube is simply a square face that has been stretched out by the same amount as the length of one side. Altogether, it looks like this:

So, I want you to try something. Picture a square. It is 4x4. Now, without rotating it in your mind, think about that square becoming a cube. In order to do that, you either push it back by 4 squares, or bring it forward by 4 squares. The back of the cube appears to be smaller, right?

It's the same thing with going to 4-D from 3-D. For us, if you had a 4-D box with one open face, it would seem like space itself was folded into the box. So if you had a 4x4x4x4 inch box, it would appear as a 4x4x4 inch box, but it would be able to hold the same amount of items as a box with a volume of 256 inches. Each cube would have a total of 4 cubes occupying what would appear in our dimension to be the same space, but in a fourth dimension, it would be expanded out.

Now, imagine you have a paper circle and a box. You are looking down into the box, and you are holding the circle towards the top of the box. As you move the circle closer to the bottom of the box, it appears to get smaller because it is further away. The same thing would happen as you moved something through 4-D space. If you took a marble and pushed it away from yourself, it would appear to get smaller, as it would be farther away. To bring an object in a fourth dimension closer, it would appear bigger, as it would be closer. The difference is, since we cannot perceive or interact with the 4th dimension the way we can with the second or third dimension, it would genuinely be bigger or smaller for us.

A good way to demonstrate this was illustrated by Charles Hinton.

"from the perspective of the two-dimensional being, a three- dimensional sphere pushed through a two-dimensional plane would appear as a point when the sphere touched the plane, grow into a circle with the same radius as the sphere, then shrink back into a point."

The same would happen with a 4-D object in 3-D space. A sphere would begin at its smallest possible size and grow to its largest size, then shrink back down to nothing. Thus, if a 3-D object were pushed through 4-D space, the same thing would happen: If it were to be moved 'closer', it would be bigger, and if it were to be moved 'away', it would be smaller.

Sites:

https://analyticphysics.com/Higher%20Dimensions/The%20Visual%20Appearance%20of%20Higher-Dimensional%20Objects.htm

TL;DR: a shrink ray is the closest thing humans have imagined to a device that can move through the 4th dimension

[i-research-so-you-dont-have-to]

Correct, but a way we could perceive movement in a fourth dimension could be something getting smaller as it moves away the same way an object gets smaller when you apply the concept of a 3D object going further away to a 2D world; if you draw a box with something at the bottom, the thing at the bottom is smaller than if it were drawn at the top. With 4D to 3D, it is the same concept, but with another dimension added.

On Four Dimensional Space

While many people think that H.G. Well's time machine was a good representation of something that could move through a fourth dimension, there is a better example: A shrink ray/growth ray.

(Explanation under the cut)

Have you ever seen this shape?

It's often called a 4-D cube, otherwise known as a tesseract, and for the longest time, I didn't understand how a cube inside a cube equaled another dimension. But I finally realized, the cube that appears smaller is actually the outside.

Let me explain. But first, I want you to imagine that you are a 2-D entity. You want to know how a square could possibly have three dimensions. You picture a square, and it looks like this:

Now, as a three dimensional being, we know that in order to make it a cube, each square is extended outward along the square by the length of one side. The problem with that is in 2-D space, you cannot have a cube. But conceptually speaking, we are aware that a cube is simply a square face that has been stretched out by the same amount as the length of one side. Altogether, it looks like this:

So, I want you to try something. Picture a square. It is 4x4. Now, without rotating it in your mind, think about that square becoming a cube. In order to do that, you either push it back by 4 squares, or bring it forward by 4 squares. The back of the cube appears to be smaller, right?

It's the same thing with going to 4-D from 3-D. For us, if you had a 4-D box with one open face, it would seem like space itself was folded into the box. So if you had a 4x4x4x4 inch box, it would appear as a 4x4x4 inch box, but it would be able to hold the same amount of items as a box with a volume of 256 inches. Each cube would have a total of 4 cubes occupying what would appear in our dimension to be the same space, but in a fourth dimension, it would be expanded out.

Now, imagine you have a paper circle and a box. You are looking down into the box, and you are holding the circle towards the top of the box. As you move the circle closer to the bottom of the box, it appears to get smaller because it is further away. The same thing would happen as you moved something through 4-D space. If you took a marble and pushed it away from yourself, it would appear to get smaller, as it would be farther away. To bring an object in a fourth dimension closer, it would appear bigger, as it would be closer. The difference is, since we cannot perceive or interact with the 4th dimension the way we can with the second or third dimension, it would genuinely be bigger or smaller for us.

A good way to demonstrate this was illustrated by Charles Hinton.

"from the perspective of the two-dimensional being, a three- dimensional sphere pushed through a two-dimensional plane would appear as a point when the sphere touched the plane, grow into a circle with the same radius as the sphere, then shrink back into a point."

The same would happen with a 4-D object in 3-D space. A sphere would begin at its smallest possible size and grow to its largest size, then shrink back down to nothing. Thus, if a 3-D object were pushed through 4-D space, the same thing would happen: If it were to be moved 'closer', it would be bigger, and if it were to be moved 'away', it would be smaller.

Sites:

https://analyticphysics.com/Higher%20Dimensions/The%20Visual%20Appearance%20of%20Higher-Dimensional%20Objects.htm

TL;DR: a shrink ray is the closest thing humans have imagined to a device that can move through the 4th dimension

[i-research-so-you-dont-have-to]

On Four Dimensional Space

While many people think that H.G. Well's time machine was a good representation of something that could move through a fourth dimension, there is a better example: A shrink ray/growth ray.

(Explanation under the cut)

Have you ever seen this shape?

It's often called a 4-D cube, otherwise known as a tesseract, and for the longest time, I didn't understand how a cube inside a cube equaled another dimension. But I finally realized, the cube that appears smaller is actually the outside.

Let me explain. But first, I want you to imagine that you are a 2-D entity. You want to know how a square could possibly have three dimensions. You picture a square, and it looks like this:

Now, as a three dimensional being, we know that in order to make it a cube, each square is extended outward along the square by the length of one side. The problem with that is in 2-D space, you cannot have a cube. But conceptually speaking, we are aware that a cube is simply a square face that has been stretched out by the same amount as the length of one side. Altogether, it looks like this:

So, I want you to try something. Picture a square. It is 4x4. Now, without rotating it in your mind, think about that square becoming a cube. In order to do that, you either push it back by 4 squares, or bring it forward by 4 squares. The back of the cube appears to be smaller, right?

It's the same thing with going to 4-D from 3-D. For us, if you had a 4-D box with one open face, it would seem like space itself was folded into the box. So if you had a 4x4x4x4 inch box, it would appear as a 4x4x4 inch box, but it would be able to hold the same amount of items as a box with a volume of 256 inches. Each cube would have a total of 4 cubes occupying what would appear in our dimension to be the same space, but in a fourth dimension, it would be expanded out.

Now, imagine you have a paper circle and a box. You are looking down into the box, and you are holding the circle towards the top of the box. As you move the circle closer to the bottom of the box, it appears to get smaller because it is further away. In 2D space, the circle is actually smaller because it cannot exist as further away in that direction, The same thing would happen as you moved something through 4-D space. If you took a marble and pushed it away from yourself, it would appear to get smaller, as it would be farther away. To bring an object in a fourth dimension closer, it would appear bigger, as it would be closer. The difference is, since we cannot perceive or interact with the 4th dimension the way we can with the second or third dimension, it would genuinely be bigger or smaller for us.

A good way to demonstrate this was illustrated by Charles Hinton.

"from the perspective of the two-dimensional being, a three- dimensional sphere pushed through a two-dimensional plane would appear as a point when the sphere touched the plane, grow into a circle with the same radius as the sphere, then shrink back into a point."

The same would happen with a 4-D object in 3-D space. A sphere would begin at its smallest possible size and grow to its largest size, then shrink back down to nothing. Thus, if a 3-D object were pushed through 4-D space, the same thing would happen from the perspective of the 3-D space: If it were to be moved 'closer', it would be bigger, and if it were to be moved 'away', it would be smaller.

Sites:

https://analyticphysics.com/Higher%20Dimensions/The%20Visual%20Appearance%20of%20Higher-Dimensional%20Objects.htm

TL;DR: a shrink ray is the closest thing humans have imagined to a device that can move through the 4th dimension