matthen

[matthen]

A simulation of a wave inside a stadium- a rectangle and two semicircles. Although it is a very simple shape, the wave function cannot be exactly solved and becomes chaotic. The simulation is actually computed on a rectangular grid of pixels as a cellular automaton- note the checkerboard patterns and pixelated edges. [more] [code]

[matthen]

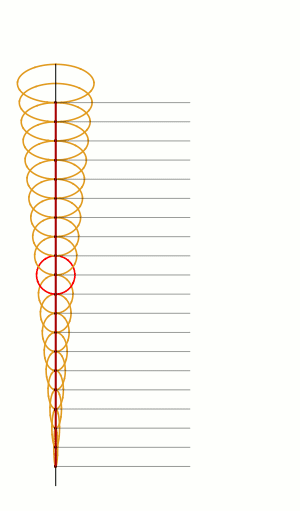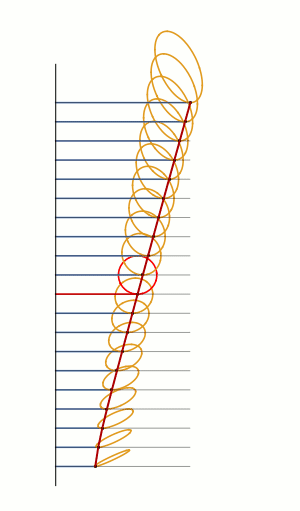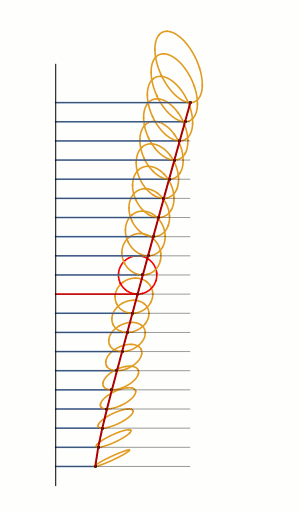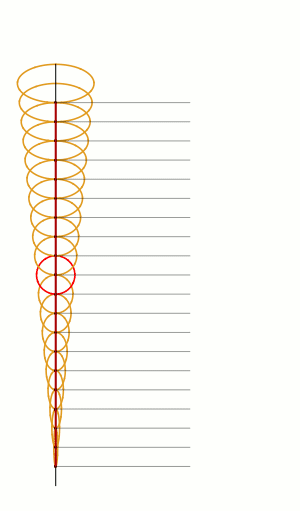
Rolling ellipses of different dimensions to measure their perimeters. The red line is the curve of perimeter versus how squashed the ellipse is. The curve is defined by an elliptic integral, and cannot be expressed with elementary functions. [code]

[matthen]

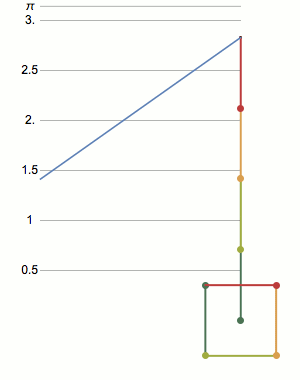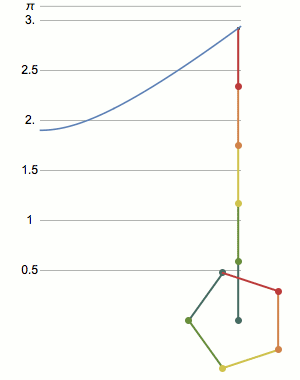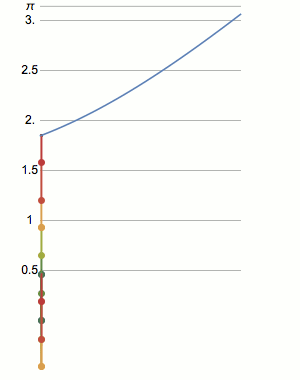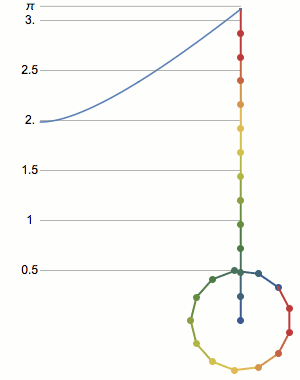
The perimeter of a squashed square drops linearly with how much it is squashed. For a pentagon, the perimeter varies in a more complicated curve. As the number of sides increases, the shapes get closer and closer to squashed circles, or ellipses. There is no closed form equation for the perimeter of an ellipse, so this curve is just defined as an elliptical function. [code] [more]

[matthen]

These three loops cannot be taken apart, but if you remove any one of them the other two will be disconnected. When any two loops are pulled apart, it’s clear that the other loop is the only thing keeping them together. These are called Borromean rings. [more] [messy code]

[matthen]

drawing shapes using waves

[matthen]

Shining a flashlight reveals the conic sections - circles, ellipses, parabolas and hyperbolas. I’ve been working on an interactive visualization of this that uses the orientation of your phone to aim the flashlight. Please try it out by visiting this link! Can you get a parabola from intersecting the cone of light with the plane below? [code] [link]

[matthen]

Water streaming inwards from a spinning tube appears to curve ahead of the spin. All individual particles travel in a straight line once they have left the tube, where they have a faster tangential speed relative to the points closer to the centre. [inspired by the exploratorium] [code]

[matthen]

Patterns of lines emerging from looking at a cubic lattice of points. The black lines form along directions in the cube where the eye can see unobstructed to the other side. [code]

[matthen]

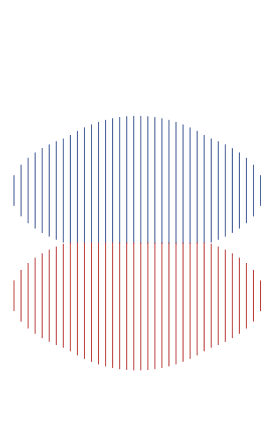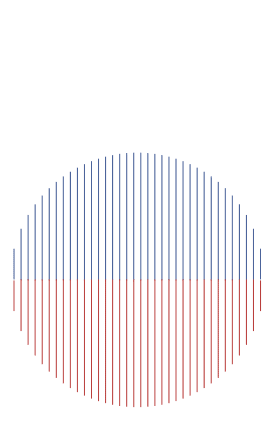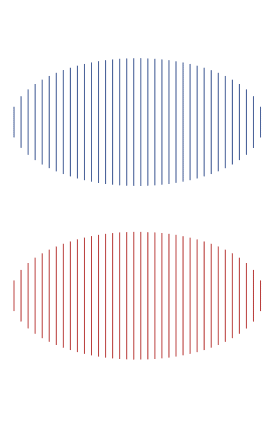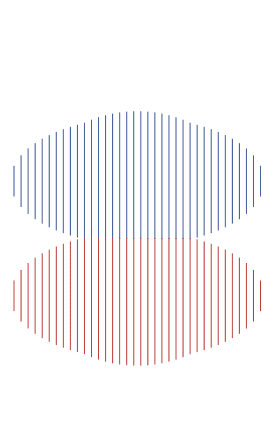
The area of two ellipses, whose heights are half their widths, adding up to a single circle. [code]

[matthen]

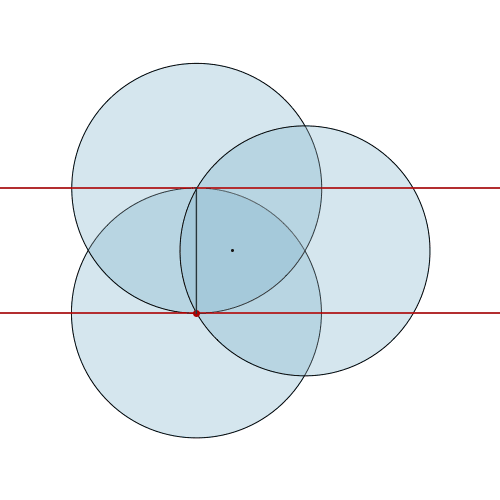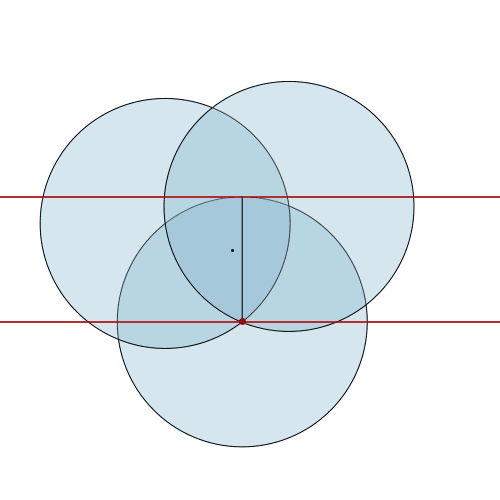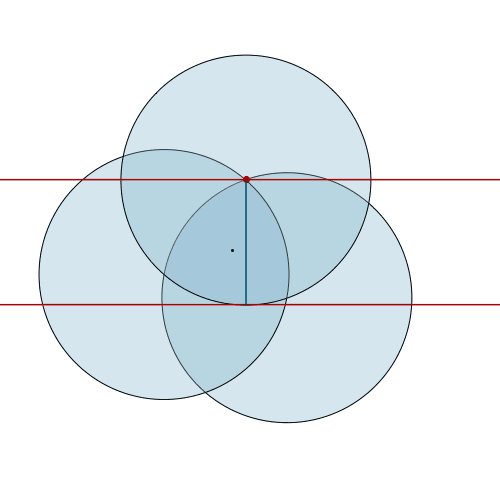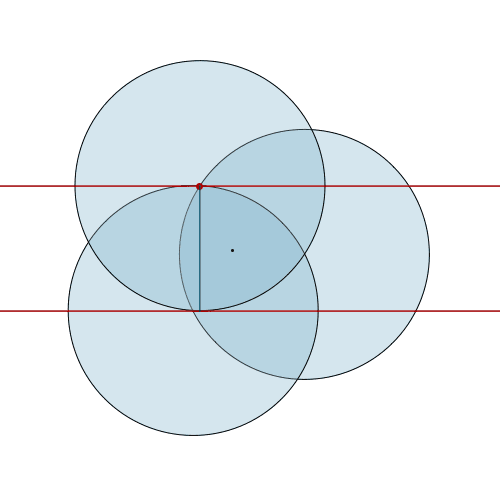
A Reuleaux triangle is built from three circles. As it rolls, its height is always the radius of one of the circles - a constant. This makes it a curve of constant width, just like a circle. [more] [code]

[matthen]

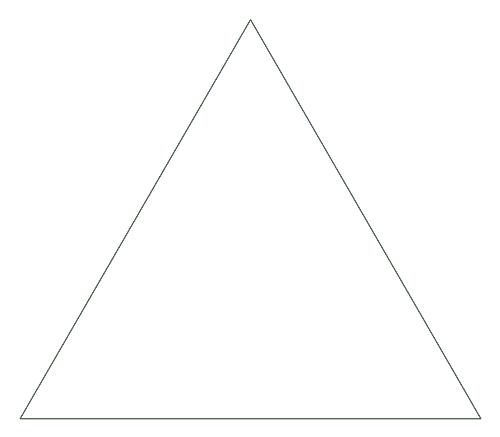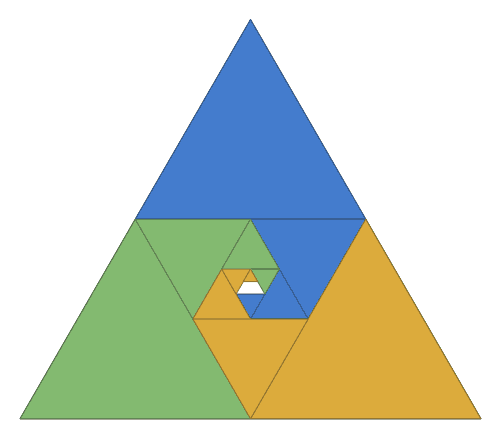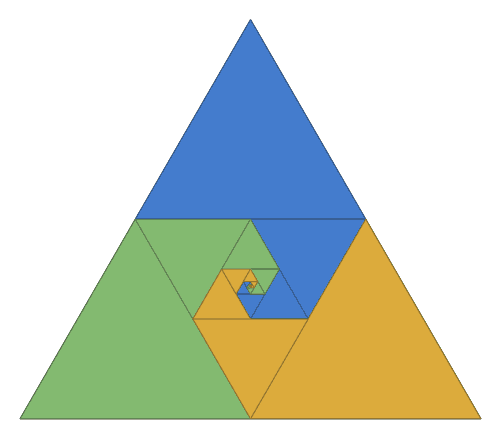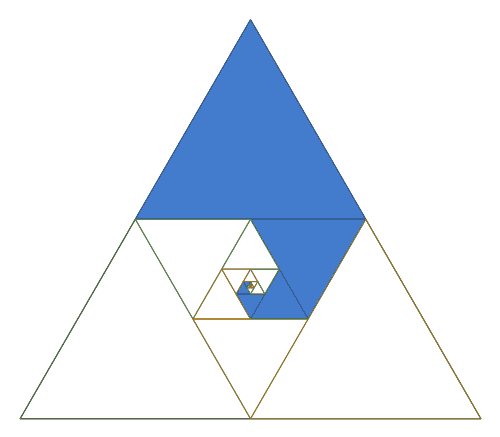
a visual proof that 1/4 + 1/16 + 1/64 + ... = 1/3 [code] 

[matthen]

Each dot chases the one before it at a constant speed, slower than the one it is chasing by a fixed ratio. As a result each dot converges to a smaller circle inside the one it is chasing. If they had the same speed, they would get closer and closer to catching up, but would take infinitely long to do so. If they were faster then they would catch up with each other in a finite length of time. What kind of spiral is traced by joining the dots? [code]

[matthen]

A dodecahedron tumbling inside a circumscribing circle. [code]

[matthen]

The primes are often thought of as behaving like a random sequence, but there are patterns in their digits. The first frame shows how many of the first 100 primes end in 1, 3, 7 and 9. They all occur roughly the same number of times, so the four squares are almost exactly the same shade of red. The next frame shows how frequently a prime ending in 1 is followed by a prime ending in 3 - and so on. A structured pattern emerges, with the final frame showing the distribution of final digits in strings of 8 consecutive primes (for the first 2 million primes).  [recent news] [visualization from] [code]

[matthen]

what is set to be the hottest social network of March 2016 - and what I have been working on in my free time recently

[matthen]

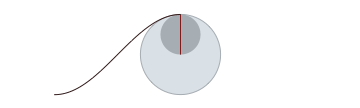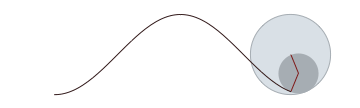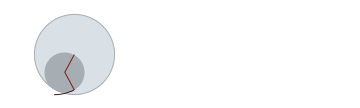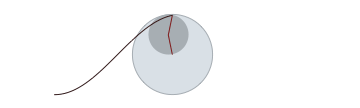
Rolling a circle in a circle to draw a cosine wave [code]

[matthen]

The focus of a rolling parabola traces out a catenary, the curve of a hanging chain held by its ends. [code] [more]