Text
Have added boolean operations to my toy MLIR compiler
Screenshot The git repo for the project now has a way to encode predicates, which I figured was a good first step towards adding some useful control flow (IF+LOOPS). Specifically, the toy language/compiler now supports the following operators: < <= > >= EQ NE This list works for any floating point or integer type (including BOOL, which is like “INT1”). I also added AND,OR,XOR (for integer…

View On WordPress
0 notes
Text
Debugging now works in my toy MLIR compiler!
Screenshot Screenshot I’ve now got both line debugging (break, next, continue) working, and variable display (and modification) debugging now working for my toy language and compiler. Here’s an example program: BOOL i1; i1 = TRUE; PRINT i1; INT8 i8; i8 = 10; PRINT i8; INT16 i16; i16 = 1000; PRINT i16; INT32 i32; i32 = 100000; PRINT i32; INT64 i64; i64 = 100000000000; PRINT i64; FLOAT32…

View On WordPress
#DIBasicTypeAttr#DICompileUnitAttr#DILocalVariableAttr#DISubprogramAttr#DISubroutineTypeAttr#getFusedLoc#LLVM IR#lowering#MLIR#mlir::LLVM::DbgDeclareOp#verify
0 notes
Text
The quest for DWARF instrumentation in a toy MLIR compiler
I’ve gotten my toy compiler project to the stage where I can generate a program, compile and run it. Here’s a little example: Screenshot This is the MLIR that is generated for this little program: "builtin.module"() ({ "toy.program"() ({ "toy.declare"() <{name = "x", type = f64}> : () -> () loc(#loc) %0 = "arith.constant"() <{value = 5 : i64}> : () -> i64 loc(#loc1) %1 = "arith.constant"()…

View On WordPress
0 notes
Text
A peek into C++ std::atomic. Extracting the meaning of std::memory_order_seq_cst.
When I worked on DB2-LUW, we had to write our own atomic implementation. Ours worked on many different types of hardware, operating systems, and compilers, so was quite representative, and matches the capabilities of the now “new” C++ interfaces. Some of that correspondence is not a surprise, since we provided our implementation to the xlC compiler team, who was advocating against…
#ARM#fetch_add#Intel#ISYNC#LDADDA#LDADDAL#LDADDL#LDAR#LDAXR#LDXR#load#LOCK XADD#LOCK XCHG#LWARX#LWSYNC#powerpc#std::atomic#std::memory_order_acquire#std::memory_order_release#std::memory_order_seq_cst#STLR#STLXR#store#STWCX.#STXR
0 notes
Text
Adding fixed size types to my toy MLIR compiler
In toycalculator, an MLIR/LLVM compiler experiment, I described a rudimentary MLIR based compiler. I’ve now added fixed size integer types, a boolean type and boolean constants (but not boolean operators), and two floating point types. For the time being, the untyped ‘DCL’ declaration type (FLOAT64) is still in the grammar and the parser/MLIR-builder. There’s lots still in the TODO list,…
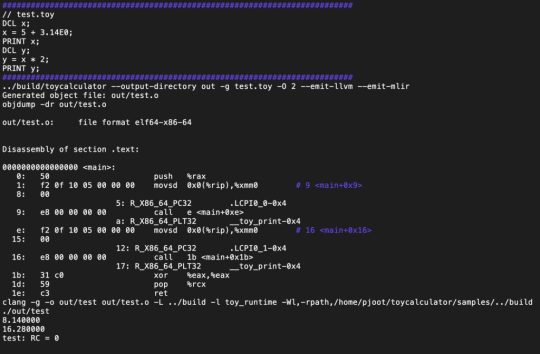
View On WordPress
0 notes
Text
toycalculator, an MLIR/LLVM compiler experiment.
Over the last 8 years, I’ve been intimately involved in building a pair of LLVM based compilers for the COBOL and PL/I languages. However, a lot of my work was on the runtime side of the story. This was non-trivial work, with lots of complex interactions to figure out, but it also meant that I didn’t get to play with the fun (codegen) part of the compiler. Over the last month or so, I’ve been…
0 notes
Text
A little float explorer program
Karl’s 1st year C programming course included IEEE floating point representation. It’s good to understand that representation, but pretty silly to try to do those conversions by hand. I remember covering this in our computer organization course, but by that time I’d already figured it out for my own purposes. I wasn’t smart enough to look it up, and figured it out the hard way by reverse…
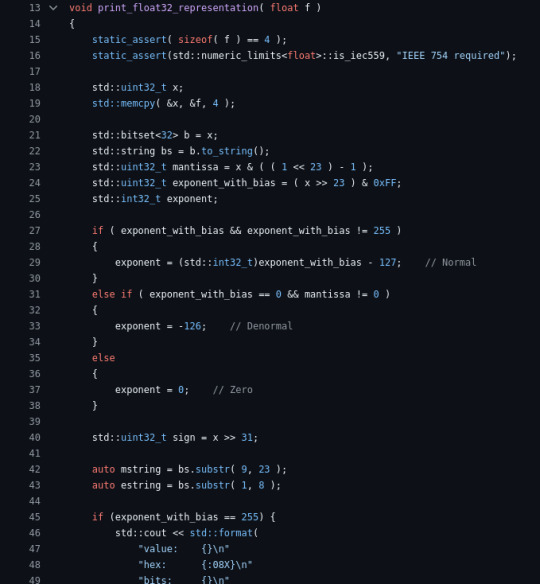
View On WordPress
0 notes
Text
more git-fu: reset --hard after force push
When I have a branch that I’m sharing only between myself, it’s occasionally helpful to force push and then reset all the other repo versions of the branch to the new one. Yes, I know that’s inherently dangerous, and I’ve screwed up doing this a couple times. Here’s one way to do it: # alias gitbranch='git branch --show-current' git fetch git reset origin/`gitbranch` --hard When I do this, I…
0 notes
Text
git diff against previous
0 notes
Text
Weighted geometric series
[Click here for a PDF version of this post] Karl needed to evaluate the sum: \begin{equation}\label{eqn:weightedGeometric:20} S = \sum_{k = 0}^9 \frac{a + b k}{\lr{ 1 + i }^k} \end{equation} He ended up using a spreadsheet, which was a quick and effective way to deal with the problem. I was curious about this sum, since he asked me how to sum it symbolically, and I didn’t know. Mathematica…

View On WordPress
0 notes
Text
Wonderful Life=Giving Radium
From “The Wide World” Magazine, June 1905 edition “This remarkable substance is absolute and quick death to the germs of cancer, tumor, consumption, malaria, blood poison, ulcers and all forms of existing disease. When it enters the system every vestige of disease is driven out, as no germ can live in its presence.” The amusing thing is that the idea of this advertisement has a close analogue…

View On WordPress
0 notes
Text
Impedance refresher.
[Click here for a PDF version of this post] Karl is taking his circuits course right now, which means that I get a chance to field some questions. I don’t get an excuse to think about this stuff any more. It’s fun material, since most of the ideas are all really simple, and you can figure out everything from first principles. Karl just started sinusoidal circuits, which I think is a bit exciting.…
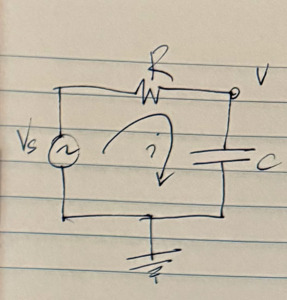
View On WordPress
#capacitor#Fourier transform#Green&039;s function#Heavyside Theta#impedance#inductor#linear system#RC circuit#reactance#resistance#RLC circuit#step function#system response
0 notes
Text
Pascal's triangle: binomial coefficients, value and recurrence relation
[Click here for a PDF version of this post] I saw an interesting solution of an introductory programming source sample problem, showing how to display Pascal’s triangle up to a given size. For example, given input \( n = 5 \), the output should be like: \begin{equation*} \begin{array}{c} 1 \\ 1 \quad 1 \\ 1 \quad 2 \quad 1 \\ 1 \quad 3 \quad 3 \quad 1 \\ 1 \quad 4 \quad 6 \quad 4 \quad 1 \\ 1…
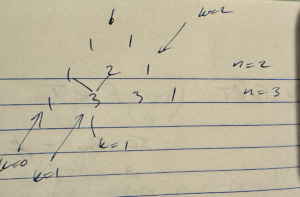
View On WordPress
0 notes
Text
Electric fields for ring and disk charge distributions (along the central axis.)
[Click here for a PDF version of this post] Motivation: explain field formulas in an engineering problem set. The following equations were given in a problem set for the magnitude of the electric field strength at a point \( z \) due to symmetric ring and disk charge distributions respectively: \begin{equation}\label{eqn:ringAndDiskField:20} E = \frac{q z}{4 \pi \epsilon_0 \lr{ z^2 + R^2 }^{3/2}…
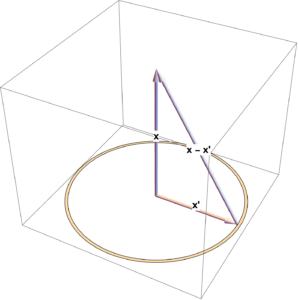
View On WordPress
#charge density#charge distribution#disk charge distribution#electric field#electrostatics#line charge density#ring charge distribution#static field#surface charge density
0 notes
Text
A Green's function solution to falling with resistance problem.
[Click here for a PDF version of this post] Motivation. In a fun twitter/x post, we have a Green’s function solution to a constant acceleration problem with drag. The post is meant to be a joke, as the stated problem is: “A boy drops a ball from a height \( h \). What is the speed of the ball when it reaches the floor (no drag)?” The joke is that nobody would solve this problem using Green’s…
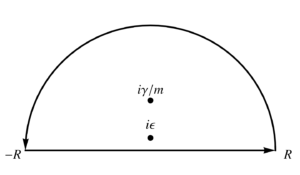
View On WordPress
#air resistance#contour integral#delta function#falling mass#Fourier transform#Green&039;s function#Jordan&039;s Lemma#offset pole#transform pair
0 notes
Text
A PV integral using contour integration.
[Click here for a PDF version of this post] Here’s the second last real-integral sub-problem from [1], problem 31(j). Find \begin{equation}\label{eqn:oscillatorKernel:20} I = P \int_{-\infty}^\infty \inv{ \lr{ \omega’ – \omega_0 }^2 + a^2 } \inv{ \omega’ – \omega } d\omega’. \end{equation} Our poles are sitting at \( \omega \), and \begin{equation}\label{eqn:oscillatorKernel:80} \alpha, \beta =…

View On WordPress
#Cauchy Principle Value#contour integral#damped oscillator#forced oscillator#integral#real integral#residue
0 notes
Text
More residue calculus: sinc squared, fractional exponent, log, pie contour
[Click here for a PDF version of this post] Sinc squared. This is problem 31(g) from [1]. Find \begin{equation}\label{eqn:sincSquared:20} I = \int_{-\infty}^\infty \frac{\sin^2 x}{x^2} dx. \end{equation} We will use the same upper half plane semicircular contour, enclosing the second order pole at the origin. This time we write \begin{equation}\label{eqn:sincSquared:40} \sin^2 x = \frac{ 1 –…

View On WordPress
0 notes