#Eadem mutata resurgo

[blacklinesw9]

Check out this awesome 'Bernoulli Spiral: eadem mutata resurgo' design on @TeePublic!

[saayawolf]

" Sebbene diversa , rinasco identica"

Il matematico svizzero Jakob Bernoulli (1654 – 1705) definì la curva “Spira mirabilis”, la spirale meravigliosa, disponendo che essa fosse incisa sull'epitaffio accanto alla frase “Eadem mutata resurgo”, ovvero "sebbene diversa, rinasco identica" ad indicare l'immortalità dell'anima, che sopravvive nonostante la fine.

[princessofmistake]

«Eadem mutata resurgo» «Seppur diversa, risorgo uguale» 🏷️ Epitaffio sulla tomba di Jakob Bernoulla

La “spira mirabilis” (spirale meravigliosa) è una spirale particolare, poiché essa non ha né inizio né fine, infatti, eseguendo infinite evoluzioni verso e dal suo polo, rimane sempre somigliante a se stessa. Per questo motivo lo scienziato svizzero Jakob Bernoulli, che la descrisse e rimase affascinato dalla proprietà di autosomiglianza della curva, la volle incisa sulla sua lapide assieme alla frase, «Eadem mutata resurgo» a indicare l’immortalità dell’anima, che sopravvive nonostante la fine della vita.

[disccover]

Medio Mutante - Eadem Mutata Resurgo ( 2015 )

[sophie-blanceur]

"Eadem mutata resurgo"

Per quanto possa cambiare,

rinasco restando la stessa.

J. Bernoulli

[terriblemaintenance]

Spoilers for Alchemy Stars 11-9!

Part One. This is part two, and there's really only one line I wanted to discuss (there was more, but it felt like splitting hairs):

But first, a refresher on how we got to this line:

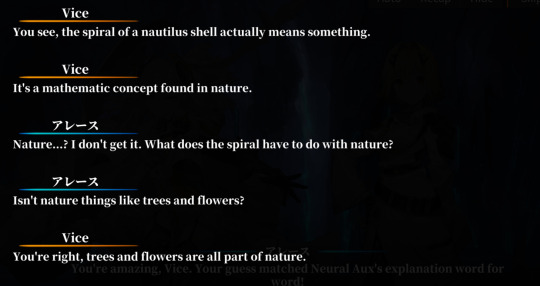
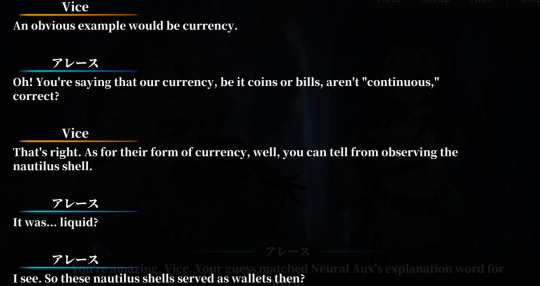
Neural Aux confirms that liquid volume was indeed the metric for transactions in the Obelisk of Return. And so we get to this part:

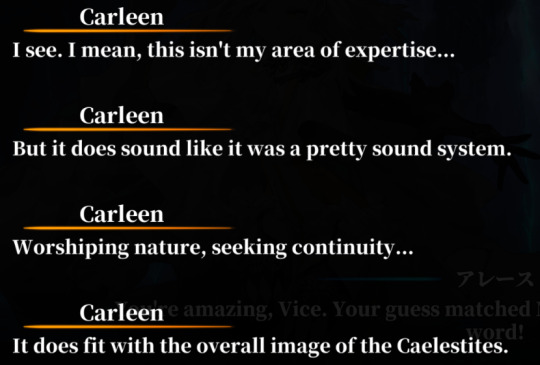
JP Version:

Carleen: I see. I don't understand the whole angle…

Carleen: But it sounds like they have a beautiful philosophy.

Carleen: Placing value on "Nature," basing a metric on "Continuity"…

Carleen: It does fit with the overall image of the Caelestites.

I checked both CN and JP versions on this and they align. CN uses 律度 (lǜ dù), and JP uses 度量衡 (doryoukou), both referring to calculating volume and weight.

Simplifying it to "worshiping nature, seeking continuity" does the lore-building a disservice and make them sound like tree-huggers.

Caelestites are scientific-minded, or in EN and CN's case, mathematically inclined. They don't put nature above all else. They were obeying the natural order of things. That was the whole point of the nautilus spiral.

Let's go back to the nautilus shell. The mathematical concept Vice refers to is a logarithmic spiral. It has a unique mathematical property: the size of the spiral increases, but its shape is unaltered with each successive curve. Ever-growing, but ever-constant.

And that is how we get to Continuity, which is yet another mathematical concept. tl;dr: a sapling can't turn into a tree instantaneously - Vice

Continuity expects tiny changes in value to ensure it gets from point to point. If there is a jump in value, there will be a discontinuity. Our spiral may no longer be an ever-growing, ever-constant spiral. Applied to the Caelestites, that means any deviation from how they are supposed to think or how they're supposed to act is going to be a discontinuity.

Hence, the Exiled Zone exists. Thoughts or acts that don't follow their acceptable (probably even predetermined) path are likely tagged seditious and/or extremist. Take out the values that jump, the spiral can continue to exist.

This whole chapter was meant to supplement the lore revealed in 11-12. And the line I quoted at the top was supposed to reinforce that they were living through those two principles, not worshiping and chasing an ideal.

Fun fact #1: An alternate translation for the Obelisk of Return (回帰の塔) is the Tower of Revolution/Recurrence. Oh, look, it's continuous-themed!

Fun fact #2: The logarithmic spiral was first studied by Descartes in 1638 and Vice Jakob Bernoulli. Vice Bernoulli was so fascinated by the spiral that he had one engraved on his tombstone [...] together with the words "eadem mutata resurgo" ("I shall arise the same though changed").

[thou-breath-of-autumns-being]

More in incorrect gravestones for famous old mathematicians: Jacob Bernoulli, who extensively studied the logarithmic spiral, wanted one on his gravestone together with the legend "Eadem mutata resurgo" due to the many transformations that when applied to it result in yet another logarithmic spiral. Well, he got a spiral, but an Archimedean (arithmetic) spiral rather than a logarithmic one, paired with text that doesn't really apply to it.

oh NO

[arseniccattails]

Eadem mutata resurgo

Some thoughts about Theseus by the Oh Hellos.

Normally the Ship of Theseus is an argument about the ontology of said ship-is it or is it not the same ship? But the song doesn’t even ask. Because you are Theseus’ ship, and despite everything against you, you made it to harbor. Instead, the question is “Is Theseus’s ship worth repairing? When it will break again and again and again?” And the answer is “of course.” Fixing the busted bits of the ship will be painful. You will get splinters. And you will have to do it again and again and again. And each time you will leave the harbor. Although changed, you will rise the same. Because, “everything about you may fall apart, but you’ll be alright.”

[s0irenic]

Eadem Mutata Resurgo 8 - ALICJA KWADE - 2014

[vanessalu]

eadem mutata resurgo* /chapter2/

[levysoft]

La spirale è quella curva piana che ha la proprietà di avvolgersi in infiniti giri intorno ad un punto. È una struttura molto diffusa in natura: dai cicloni alle galassie, dalle corna d'alcuni animali (come i montoni) fino alle conchiglie, dal moto dei cicloni alla molecola del DNA, dai fiori di girasole fino alle zanne degli elefanti.

(fig. 1: Un'ammonite del Madagascar tagliata in due parti. In ciascuna di esse è visibile una spirale logaritmica.)

Un tipo particolare di spirale è la spirale logaritmica.

L'equazione in coordinate polari è la seguente: dove è l'angolo costante formato dal raggio e dalla tangente.

(fig. 2: la spirale logaritmica.)

La spirale logaritmica si può pensare ottenuta anche nel seguente modo. Consideriamo una semiretta che ruota uniformemente intorno ad un suo estremo ed un punto che si muove lungo questa semiretta con velocità che aumenta man mano che il punto si allontana dall'estremo fissato. Il punto traccia una curva che è appunto una spirale logaritmica.

Il matematico Jacques Bernoulli (1654-1705) fu un grande studioso di curve e rimase particolarmente affascinato dalla spirale logaritmica. Ne dimostrò molte proprietà inedite e volle che fosse incisa sulla sua tomba accompagnata dal motto Eadem mutata resurgo (Trasformata nella dimensione, rinasco sempre uguale).

Infatti, osservando la figura si nota che la spirale logaritmica prosegue indefinitamente sia verso l'interno sia verso l'esterno: la curva si avvolge intorno al punto centrale senza mai raggiungerlo. Il centro della spirale logaritmica, osservato con un qualsiasi ingrandimento, appare costantemente come una spirale infinita.

In conclusione la spirale logaritmica è una figura autosimile e di conseguenza può essere considerata un frattale. Per la precisione si tratta di un frattale con condensing.

La spirale logartmica può essere ottenuta considerando come figura di partenza un punto posto ad una certa distanza dall'origine ed applicando a questo punto una similitudine. Nella figura che segue il punto di partenza è evidenziato in rosso. La figura ottenuta è una spirale logaritmica.

La similitudine applicata è ottenuta componendo una omotetia con rapporto di omotetia K minore di 1 ed una rotazione. Naturalmente il risultato ottenuto cambia al variare dei coefficienti.

Considerando come figura di partenza una circonferenza si ottengono figure simili ad una conchiglia.

Per maggiori particolari sulle curve consiglio il libro Le Curve celebri di Cresci. Invece per conoscere tutte le infinite applicazioni della spirale in natura consiglio il testo Che forma ha un fiocco di neve di Stewart.

Altri esempi di spirali nel sito si possono trovare nella sezione dedicata alla composizione di trasformazioni geometriche.

Inoltre due pagine sono dedicate alle spirali nelle piante grasse: una con le foto più leggere, un'altra con foto più grandi.

[sophie-blanceur]

"Eadem mutata resurgo"

Per quanto possa cambiare,

rinasco restando la stessa.

J. Bernoulli

[nosce]

¿Me amas? El desierto es Circular. Para encontrar a los Cuatro Maestros tendremos que viajar en ESPIRAL. Eadem Mutata Resurgo.

¿Me amas? El desierto es Circular. Para encontrar a los Cuatro Maestros tendremos que viajar en ESPIRAL. Eadem Mutata Resurgo.

[raennox]

EADEM MUTATA RESURGO