#Eulerian trail

[summercurial]

One-upping kat by having a eulerian sex trail

wait. what would be the sex trail here (i guess you could have a trail from successive sex acts? this would be hard to orchestrate). or did you mean eulerian sex graph. anyway my sex graph is presumably not eulerian because some people way out in the conections to the dudes ive fucked have an odd count

[alywats]

Eulerian Graphs

Eulerian Graphs are a classification of combinatorial graphs in which there exists a closed trail that includes every edge of the graph (a closed trail is a way to traverse a graph in which all edges traversed are distinct, and the starting vertex is the ending vertex). This trail is referred to as the Eulerian Trail of a graph.

    The name Eulerian Graph comes from Leonhard Euler, who wrote a paper in 1735 on the Königsberg Bridge Problem, a famous problem that asks if you can cross each of these seven bridges and return to your starting point. This problem, which was solved by Euler in his paper is the same as asking whether this figure has an Eulerian trail. Another typical problem on this topic may ask whether a graph can be drawn without lifting the pencil or backtracking.

    This leads to perhaps the first theorem in graph theory and the first proof in the study of networks, credited to Euler; that states that a connected graph is Eulerian if and only if the degree of each vertex is even. We can see that this is true because for any vertex you pass through when traversing the graph there will be two edges you traverse, and since every edge must be traversed and you have to start and end at the same vertex, every vertex has an even degree. Going the other direction, if every vertex has even degree, then the graph has a cycle (a proven result). Then using induction, it can be shown that by removing an edge and finding an Eulerian trail in this smaller graph, and then adding the edge back in, there will be an Eulerian trail in the original graph.

    Following from Eulerian graphs are semi-Eulerian graphs. These are graphs which have a non-closed Eulerian trail, or in other words, every edge is traversed but the starting and ending points are different. Semi-Eulerian graphs have exactly two vertices of odd degree, the starting and ending point. This can be proven in a similar fashion.

We can also note that it is impossible for a graph to have only one vertex of odd degree by the Handshaking lemma --credited to Euler as well. The Handshaking lemma states that the total degree of any graph must be even. This because every edge is connected to two vertices, and this implies that the total degree of a graph is twice the number of edges and therefore even.

Next we can apply these same definitions and theorems to directed graphs, noting that an Eulerian digraph must be strongly connected, meaning that the outdegree (arcs pointing out from a vertex) and the indegree (arcs pointing towards a vertex) must be equal for any vertex in the graph.

Infinite Eulerian graphs are connected countably infinite graphs that contain a two-way infinite trail that contain every edge. The necessary and sufficient conditions are altered slightly to account for the infinite components of the graph, but still require every vertex to have even degree.

    A similar problem arising after the Königsberg Bridge problem is the five rooms problem where you have to go through five rooms and get back to where you started without backtracking. This is impossible since when this scenario is turned into a graph, with vertices being the rooms and edges being walls, there are vertices of odd degree.

    Problems concerning Eulerian graphs are often related to recreational mathematics and drawing games, but there are some very important applications as well. In 2001, a group of biologists used Eulerian trails to better understand DNA fragment assembly.

    Graph Theory is a relatively new area to be explored in mathematics, but its foundations date back to the mid 1700s with Euler. By looking at the Bridge problem and the Handshaking lemma in an abstract way, he laid the basis for modern graph theory, which in turn is the basis for thinking in computer science.

[hippasos]

I have to confess that I don’t really know, if childeren in other countries play this game, but in Germany we draw the “house of Saint Nicholas”. And children are saying the syllables

“Das-ist-das-Haus-vom-Ni-ko-laus.”

(Translation: “This-is-the-house-of-Ni-cho-las.”)

for each line they draw, while they draw a house in the way which is shown above. The only rules are the following:

1.) You have to draw the lines without lifting the pen.

2.) You have to draw "complete” straight lines .

There are several ways to do this.

Graph theory sayes something about the existence of drawing such an object. In Graph theory we consider a bunch of vertices which are connected with edges (lines). The Graph for the “Haus vom Nikolaus” is shown in the picture.

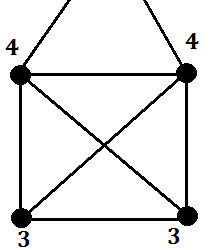
The way of drawing the house described above is called an Eulerian trail, i.e. a value of the form

  v1 e1 v2 e2 v3 ... e(n-1) v(n)

where e1,...,e(n-1) are the edges and v1,...,vn are the vertices. Such a value has the special property as an Eulerian trail that we go no edge twice or more times.

We also need to know the degree of a vertex. The degree of a vertex is the number of edges which lead to this vertex. For example the degree of the edges of the “Haus vom Nikolaus” is shown in the picture.

One can show the following: If the degree of all edges is even, then there exists an Eulerian cycle, i.e. an Eulerian trail which starts and ends at the same vertex. An Eulerian trail (which is not an Eulerian cycle) exists, if the degree of two edges is odd and the degree of the other edges is even.

If we consider the graph of the “Haus vom Nikolaus”, we see that we have two edges of odd degree (3) and three edges of even degree (2 and 4). So we have an Eulerian trail which is not an Eulerian cycle. This means, that we can draw the “Haus vom Nikolaus” considering the rules described above.

Another interesting object is the problem of the Seven Bridges of Königsberg (1736). You can find a graph decribing the problem. With the rules we formulated above for an Eulerian trail, you can easily check, if it is possible to find a way over the 7 bridges without going a bridge twice or more times. Here is the link of this interesting historic problem which Euler solved:

https://en.wikipedia.org/wiki/Seven_Bridges_of_K%C3%B6nigsberg