#Finding All Zeros of a Polynomial Function Using The Rational number

[excellentideasineducation]

If the square of the difference of the zeros of the quadratic polynomial...

[jessecmckeown]

Hermite-Lindemann

I'm still gonna say I'm on Vacation

Until last week or so, I had spent most of my life feeling confused about all the proofs of the Hermite-Lindemann Theorem I'd ever read. The proof Lang gives in Algebra involves counting small-normed small-integer combinations of vectors-of-interest, and somehow (I still can't tell you) the assumption of one vanishing combination of exponentials gives too many small-normed small-integer combinations. Otherwise, all the proofs I'd seen were of the form: $$ \mathrm{interest} = p\mbox{-coprime integer} + \mbox{too-small} $$ but where the equations came from, and the coprimality, was always messy and mysterious. I dont know if the following will be any better for you, but ... well, it's finally in a state that I find memorable, so here it will stay. The heart of any proof of the Hermite-Lindemann Theorem has to be the differential equation $$ \frac{d}{dx} e^x = e^x $$ being valid over $\mathbb{C}$. The way it shows up will be more or less obscure, from proof to proof: Spivak's specialized proof appears to wrap it up in the Gamma function, $ n! = \int_0^\infty x^n e^{-x} dx $; Weber (reported by Dörrie) conceals it in the power series $$ e^x = 1 + x + \frac{x^2}{2!} + \dots $$ but the Main Thing is that differential equation. We lean more towards Spivak's arrangement, and still more as he explains things in his proof that $\pi$ is not quadratic over $\mathbb{Q}$, though we don't much care about the Gamma Function, nor any other Improper Integrals. Instead (and, indeed, it is implicit in Spivak's argument) we use finite-domain integration-by-parts: $$ \int_0^Z P(z) e^{-z} dz = \left[\sum P^{(k)}(0)\right] - e^{-Z} \left[ \sum P^{(k)}(Z) \right]$$ where $P$ is a polynomial (so that the sums are finite) The use of this is that we can re-arrange the terms thus: $$ e^Z \sum P^{(k)}(0) = \sum P^{(k)}(Z) + e^Z \int_0^Z P(z) e^{-z} dz. $$ which is to say: up to a common denominator (a sum of derivatives at zero) several different values of the analytic object $e^Z$ can be estimated in terms of finitary algebraic data (the sum of derivatives at various $Z$) and a controllable error (the remainder integral). For example, the special case $P(x)=x^n$ gives the $n$th order Taylor series $$ n! e^x = x^n + n x^{n-1} + n(n-1)x^{n-2} + \dots + n! + e^x \int_0^x z^n e^{-z} dz $$ while the more-exotic $P(x) = x^n ( z - x)^n $, applied specifically to $\int_0^z\cdots$, gives the order $(n,n)$ Padé approximation

$$ e^{z} = \frac{1 + \frac{z}{2} + \frac{z^2}{2!2^2} + \cdots + \frac{z^n}{n!2^n} }{1-\frac{z}{2} + \frac{z^2}{2!2^2} - + \cdots + \frac{(-z)^n}{n!2^n}} + \varepsilon_\mathrm{exercise} $$ those fractions are wrong... which may seem weird... but Padé-ness is correct! see here, e.g.

Carefully crafting $P$ in terms of the minimal polynomials of certain algebraic numbers, we can get useful estimates relating the exponential function evaluated at several conjugate algebraics. Likely enough there are various feasible strategies for choosing a fruitful polynomial $P$; we will suppose that $x R(x)$ is a square-free polynomial over $\ZZ$, and ask for $$ P(x) = x^m R(x)^{a-1} \tag{%%} $$ where $a$ is some large prime and $m$ is less than the degree of $R$. The elementary symmetric functions of the roots of any polynomial over $\ZZ$, such as $R$, are the normalized rational coefficients of $R$, and hence have common denominator dividing the leading coefficient: $$ R(x) = H x^\rho + \cdots + R(0) $$ $$ H \sigma_k (x|R(x)=0) \in \ZZ $$ so by Gauss' integral factorization theorem, any symmetric polynomial in the roots of an irreducible factor of $R$ of degree $k$ with integer coefficients has denominator dividing $H^k$. In particular, whether $P$ is of form (%%) or not, $$ H^{\mathrm{deg} P} \sum_{R_i(Z)=0} \sum_j P^{(j)}(Z) \in \ZZ $$ when $P$ is of the form (%%), we can reduce sums mod $a$, by the fact that a root of $R$ is a multiple-root of $P$ $$ H^{m+(a-1)\rho} \sum_{R_i(Z)=0} \sum_j P^{(j)}(Z) \equiv H^{m+(a-1)\rho}\sum_{R_i(Z)=0} D^{(a-1)} \left( Z^m R(Z)^{a-1} \right) \\\\ \equiv H^{m+(a-1)\rho}\sum_{R_i(Z)=0} (a-1)! Z^m (R'(Z))^{a-1} \pmod{a} \tag{mod-a}$$ In the first simplification, applying $a$ or more derivatives incurs a factor of $a$, while applying fewer than $a-1$ derivatives produces a polynomial with a root at $Z$; as does distributing fewer than one derivative to any factor $R$ in $P$, in the second simplification. The purpose of the factor $x^m$, in $P(x)$, appears when estimating $$ \left(\sum_j P^{(j)}(0) \right) \left( \sum_i C_i \sum_{R_i(Z)=0} e^Z \right) = \sum_i C_i \sum_{R_i(Z)=0;j } P^{j}(Z) + \sum_i C_i \sum_{R_i(Z)=0} e^Z \int_0^Z P(z) e^{-z} dz . $$ The simplification (mod-a) then gives $$ \left(\sum_j P^{(j)}(0) \right) \left( \sum_i C_i \sum_{R_i(Z)=0} e^Z \right) = \frac{a N}{H^{m+(a-1)\rho}} + \sum_i C_i \sum_{R_i(Z)=0;j } Z^m (R'(Z))^{a-1} \\\\ {} + \sum_i C_i \sum_{R_i(Z)=0} e^Z \int_0^Z P(z) e^{-z} dz ; $$ and, while any one sum $\sum_i C_i \sum_{R_i(Z)=0;j } Z^m (R'(Z))^{a-1}$ could well be zero, nonetheless the $\rho$ vectors $(\dots,Z^m,\dots)$ for $m\in \{ 0, 1, \dots, \rho-1\}$ are independent, so that fixing $a$, there is some $m$ less than $\rho$ for which the needed combination of $Z^m$ with coefficients $C_i (R'(Z))^{a-1}$ is nonzero — and, echoing the "sneaky" method around "Derivative Remarks", the expression makes sense and has an invariant meaning in $\ZZ/(a) \lt \mathbb{F}_{a^\lambda}$, which is to say that the non-vanishing also holds $\pmod{a}$, as soon as $a$ is larger than [$\rho$, the coefficients of $R$, and some $C_i$]. And now for some estimates. The "Algebraic" Sum $$ \mathrm{Alg} = H^{m+(a-1)\rho} \sum_i C_i \sum_{Z,j} P^{(j)}(Z) $$ is an integer, but more: $P^{(j)}$ is a multiple of $j!$; and the terms $P^{(j)}(Z)$ with $j\lt a-1$ are zero, so that the nonzero $P^{(j)}(Z)$ are values of polynomials divisble by $(a-1)!$. Since we've conspired that it be Not Zero, $$ |\mathrm{Alg}| \geq (a-1)! $$ At the same time, the Analytic Error, $$ \varepsilon = H^{m+(a-1)\rho} \sum C_i e^Z \int_0^Z P(t) e^{-t} dt $$ is easily controlled. The polynomial $R$ has $\rho$ roots: suppose the largest to have norm $M$, and the degree of $P$ is $m + (a-1)\rho$, so $$ |\varepsilon | \leq (H M)^{m+(a-1)\rho} e^M \rho \sum |C_i| $$ so if $\sum C_i e^Z $ be zero, then we have, for arbitrarily large primes $a$, $$ \kappa X^a \gt (a-1)! $$ which cannot be.

the usual Hermitte-Lindemann theorem, however, makes no mention of conjugacy, and applies to algebraic coefficients $C_i$. But reducing to the present case ... is a good exercise.

[flexmathtopics-blog]

- Meaning

A zero or root of a polynomial function is a number that, when plugged in for the variable, makes the function equal to zero. To find all the zeros of a polynomial function and the possible rational roots of a polynomial equation, use the rational zero theorem.

- Links and Image for a deeper understanding of Zeros of Polynomial Function

[ss1986us]

ncert solutions for class 7 maths

class 7 maths

 Foundation of any subject is important specifically when you are taking about maths . maths is important subject for your academic journey and class 7 maths build your interest as well we as solid foundations in the subject in this class you start learning the algebra and its applications . so always take class 7 maths studies seriously . you must be wondering what is the best approach to study class 7 maths ? how to score good marks in class 7 maths ? so to answering to your questions lets discuss the right approach of studying class 7 maths .

 Right approach to study class 7 maths

 About class 7 Books: Selection of right books will help you to have better understanding of the concepts so always make NCERT maths book for class 7 your primary book , follow the sequence of chapters given in NCERT book don’t skip any chapters . after doing NCRET take a reference book or follow entrancei notes which are prepared such a way that it will build your solid foundation in class 7 maths 

About class 7 maths class: Always attend the class in school or in tuitions never skip any class , if you have any work or family function or you are sick plan the missing topic during the holidays and be reedy your topics before the next class. In class listen what teacher wants to explain and make all important points notes in your note book . ask your questions don’t hesitate while asking silly questions in class 7 maths .   

Brief descriptions about Important Chapters covered in class 7 maths

 1. Class 7 maths chapter- NUMBERS

 Natural Numbers: The counting numbers are called Natural Numbers.

          Thus, N = {1, 2, 3, 4, 5,....} is the set of all natural numbers.

Whole Numbers: Whole Numbers are simply the numbers 0, 1, 2, 3, 4, 5, …

           Thus,   W = {0, 1, 2, 3, 4, 5.....} is the set of all Whole Numbers.

Integers: Integers are like whole numbers, but they also include negative numbers ... but still no fractions allowed!

 So, integers can be negative {-1, -2,-3, -4, -5, … }or positive {1, 2, 3, 4, 5, … }, or zer{0}

We can put that all together like this:

              I or Z = { ..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ... }

Rational Numbers: A rational number is a number that can be written as a ratio (p/q form). That means it can be written as a fraction, in which both the numerator (p) and the denominator (q) are integers and q not zero.

The number 8 is a rational number because it     can be written as the fraction 8/1.

Likewise, 3/4 is a rational number because it     can be written as a fraction.

Even a big, clunky fraction like     7,324,908/56,003,492 is rational, simply because it can be written as a     fraction.

 Equivalent rational numbers: Numbers that have the same value but are represented differently.

 2.  Class 7 maths chapter- DIVISIBILITY TESTS, SQUARES, CUBES,SQUARE AND CUBE ROOTS

OVISIBILITY

DIVISIBILITY TEST:

Test of Divisibility by 2 : A number is divisible by 2, if its units digit is any of the digits 0, 2, 4, 6 and 8.

 Example:  Each of the numbers 24, 36, 78, 192, 310, 214166 is divisible by 2.

Prime Factors: A factor of a given number is called a prime factor if this factor is a prime number.

Example: The factors of 42 are 1, 2, 3, 6, 7, 14, 21 and 42. Out of these 2, 3 and 7 are prime numbers. Therefore, 2, 3 and 7 are the prime factors of 42.

 Common Factors: A number which divides each one of the given numbers exactly, is called a common factor of each of the given numbers.

 Example: 4 divide each one of 212 and 356 exactly. Therefore, 4 is a common factor of 212 and 356.

H.C.F. (HIGHEST COMMON FACTOR) OR G.C.D. (GREATEST COMMON DIVISOR) :

 H.C.F. or G.C.D. of two or more numbers is the greatest number that divides each one of them exactly.

 3. Class 7 maths chapter- ALGEBRAIC EXPRESSIONS AND IDENTITIES

 In the previous class, we have learnt about algebraic expressions and their addition and subtraction. In this chapter we shall study multiplication and division of algebraic expressions in the form of monomials and binomials etc.

Constants: A symbol having a fixed numerical value is called a constant.

Variables or Literals: A symbol which takes on various numerical values is known as a variable or a literal.

We know that the perimeter of a square of side a is given by the formula, P = 4a.

Here 4 is a constant, while a and P are variables.

We may give any value to a and get the corresponding value of P.

Algebraic Expressions : A combination of constants and variables, connected by +, - , and is known as an algebraic expression.

Types of algebraic expressions:

 1.           Monomial : An algebraic expression containing only one term, is called a monomial.

2.            Binomial : An algebraic expression containing 2 terms is called a binomial.

3.           Trinomial: An algebraic expression containing 3 terms is called a trinomial.

4.           Multinomial: An algebraic expression containing more than 3 terms, is called a

              multinomial.

Factors of A Term: When numbers and literals are multiple to form a product, then each quantity multiplied is called a factor of the product. A constant factor is called a numerical factor while a variable factor is called a literal factor.

Constant Term: A term of the expression having no literal factor is called the constant term.

Coefficients: Any factor of a term is called the coefficient of the product of other factors.

4. Class 7 maths chapter- EXPONENTS

 INTRODUCTION:

we know that can be written as that is read as two raised to the power three. Similarly, 10 times = , read as three raised to the power ten. In general, if x is any number and m is a positive integer, then we have

m times.

 The number x is called the base and m is called the exponent or the index of the exponential expression.

 5. Class 7 maths chapter- FACTORISATION

Factorisation:

When an algebraic expression can be written as the product of two or more expressions, then each of these expressions is called a factor of the given expression.

 G.C.F. or H.C.F of Monomials: The greatest common factor of given monomials is the common factor having greatest coefficient and highest power of the variables.

G.C.F. or H.C.F of Monomials = (G.C.F. or H.C.F of numerical coefficients)

(G.C.F. or H.C.F of literal coefficients)

 6. Class 7 maths chapter- SETS

 Objects: Everything in this universe, whether living or non living, is called an object. Well-defined collection of objects : A collection of objects is said to be well-defined if itis possible to tell beyond doubt about every object of the universe, whether it is there inour collection or not.

Set :       A well-defined collection of objects is called a set.

              The objects in a set are called its members or elements.

              We usually denote sets by capital letters A, B, C etc.

              If x is an element of a set A, we say that x belongs to A and we write, .

              If x does not belong to A, we write.

              There are two methods of describing a set :

              (i)     Roster Method or Tabulation Method.          

              (ii)    Description Method or Set-builder Form.

 7. Class 7 maths chapter- QUADRATIC EQUATIONS

 Quadratic Equations: A polynomial of degree 2 when equated to zero, gives an equations, called a quadratic equations.

Solving Quadratic Equation:

By solving a quadratic equation, we mean finding its roots.

Zero Product Rule:

If a and b are any two numbers or expressions, then ab = 0 a = 0 or b =0.

    8. Class 7 maths chapter- LINEAR EQUATION IN TWO VARIABLES

 In this chapter we shall we shall learn how to solve linear equations in two variables. For this we shall learn graphical representation of a point in a plane. We shall represent a point with the help of two numbers known as coordinates of that point. The concept of coordinates was given by the French Mathematician Rene Desartes, which integrates Algebra and geometry.

 9.  Class 7 maths chapter-  SPEED, DISTANCE AND TIME

Speed: The rate of change of distance is known as speed.

When an athlete runs a race, the change in the time taken is directly proportional to the change in the distance covered. A change in speed is directly proportional to the change in distance covered. More the speed more is the distance covered in the same time.

Units of Speed: Speed is measured in i) meters/ second or m/s

                                                ii) Kilometers/ hour or km/hr

 10. Class 7 maths chapter- Simple Interest:

                               When money is borrowed, interest is charged for the use of that money for a certain period of time. When the money is paid back, the principal (amount of money that was borrowed) and the interest is paid back. The amount of interest depends on the interest rate, the amount of money borrowed (principal) and the length of time that the money is borrowed.

                             Simple interest is generally charged for borrowing money for short periods of time. Compound interest is similar but the total amount due at the end of each period is calculated and further interest is charged against both the original principal but also the interest that was earned during that period.

                               Interest = Principle x rate of interest x time

   CO

ORDINATE SYSTEM

[davetutsacademy-blog]

2019 FURTHER MATHEMATICS EXAM PREP

This is the Exam Prep for your Further Mathematics Examination. We will work through one of the past questions from WAEC as we prepare you for academic excellence in your exam.

Going all the Way with you

We will work through the detailed solution to the Theory Paper of WAEC WASSCE GCE 2018 Exam in a bid to prepare you ahead of your Exams.

As an advocate for academic excellence, what I will like you to do is to first attempt the question on your own. Don't be afraid of making mistakes. You learn by trying, by failing, and then by success. Only check the solution presented here after you have made a judicious attempt on each question.Remember that there is no "singular right way" to go about solving the questions. Just check for consistency in the rules and formulae and guidelines as you work along.

The video link to the solutions are included and if you feel you need further explanations, simply check out the video to enhance your study. But make sure you attempt the question first. For this reason, the blog is broken such that you have to “READ MORE” to see the solution to the question attempted.

Who we are

At Davetuts Academy, we explores the STEM subjects with the aim of preparing students for academic excellence in their O' Level, A'Levels, JAMB UTME, POST-UTME, GED, GCSE and IGCSE exams. We feature comprehensive solution to examination past questions as we explore the basics of the STEM subjects and utilize appropriate soft tools with tips and tricks to prepare students for academic excellence.

Have a look at our welcome video below:

If by any means you find this exam prep useful, then go ahead and share and subscribe to our YouTube channel, Davetuts Academy as we aim at building academic excellence together!

So here we go with the Exam Prep for Further Mathematics. All the best with the questions!

A Question on Surd

So first, question 1 from WAEC WASSCE 2018 Further Mathematics Exam:

This is a question on surd operations and you just need to follow the correct steps in evaluating multiplication of surds and then finding the conjugate as appropriate.

The solution is shown below and you can watch the accompanying video for better understanding on how to solve such questions.

Watch the video solution by clicking here.

Evaluating the Upper Limit of a Definite Integral

Question 2 below is a question on definite integral. Go ahead and lay your hands on it.

All you have to do to solve this question is to integrate with respect to x, substitute for the upper and lower limit, and subtract the lower limit function from the upper limit function which is an equation in variable t. The catch is that you have to pick the appropriate value for t from the resulting quadratic equation.

The solution is shown below and you can watch the accompanying video for better understanding on how to solve such questions.

Watch the video solution here.

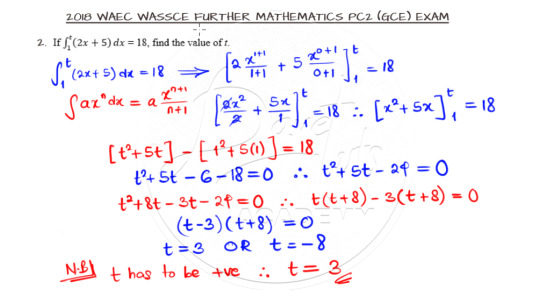
Algebra of Matrices

The next question is on Algebra of matrices. Attempt it first before moving on.

You have to understand the multiplication of matrices to evaluate the square of B and correctly define the identity Matrix I. Once that is done, the matrix N can be evaluated easily.

Click here to watch the video solution to Question 3.

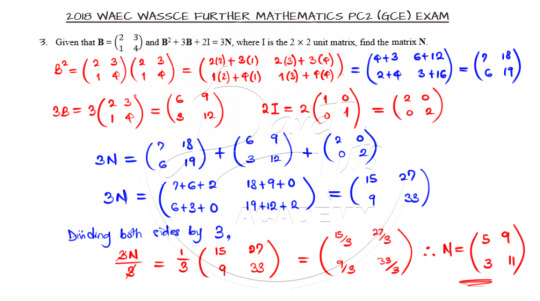
Transform the Equation of a Circle

Question 4 is based on the equation of a circle. Go ahead and try solving on your own first before checking out the solution presented.

Key stuff to simplify the solution include the general equation of a circle and the standard equation of the circle. Furthermore, the process of using completing the square to transform the general equation to the standard equation is quite important to the solution as shown below:

And here is the video for your further study.

Unordered Selection of Fruits

An unordered selection of fruit is to be carried out in question 5 from combination and you can work it out first.

The confusion to avoid here is the matter of ripe and unripe oranges. Once you can sort that out, the combination formula comes in handy to solve the question.

Click here to watch the accompanying video solution.

Estimate Mode using the Graph

Question 6 is asking us to estimate the modal age of a number of workers using graphical method. So bring out the graph paper and let’s get to work.

Obviously, you need to know the type of graph that can be used to get the mode of a set of data. And histogram is the go-to diagram to help us out. But first, you have to generate your table of values featuring the class boundary. And then you note the highest bar and cross from the adjoining bars to get the point of intersection which can be traced to get the mode.

If you still have some glitches, click here for the video solution.

Finding an Angle of a Triangle using Vector Method

Vectors is here!!! I so much love vectors. And this question is asking us to use vector method to solve for one of the angles of a triangle. So try it out.

First, locate the vertices of the triangle and then you will observe that the point Q is the point at which the angle is to be evaluated. So, taking vectors PQ and RQ, you can find the dot product from which the angle of inclination of the two vectors can be evaluated to yield the answer. 

Watch the video solution by clicking on this line. 

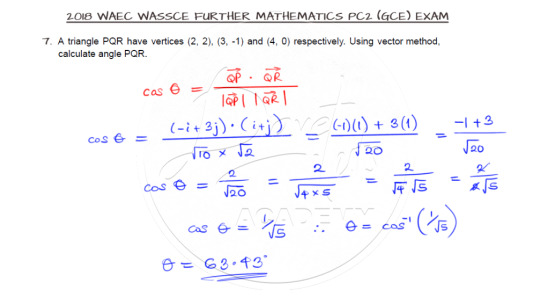
A travelling Motorist in Linear Motion

Next is question 8 based on a travelling motorist. Try it out, please.

So we need the Linear equations of motion to handle this question. But you have to interpret the question correctly before you can get it right. And there are at least two ways to go about answering this question. One way to solve it is given below.

Click here to watch the video. 

Equation of the Side of a Triangle

Question 9 asks us to evaluate the equation of a line, but not just any line. It is the side of a triangle whose vertices were given. So go ahead and try solving the question.

You need to know that joining the midpoints of two sides of a triangle will yield a line parallel to the third side and since two parallel lines have the same slope, the question can be solved by using the coordinate of the midpoint of the line AB as requested.

Further clarity are presented here in the video solution

Simultaneous Equation + Quadratic Factors

Question 10a is combining a problem on simultaneous equation and factorization of a quadratic polynomial. Try it out and make sure you are on track by making use of your calculator.

To solve this question, you will have to solve a set of simultaneous equations in 3 variables. This will enable you to solve for the values of p, q and r. The resulting quadratic equation can be factored out to get the factors of the given function.

The video solution is presented here. 

Expressing Rational Function in Partial fractions

Partial fraction is the next question in 10b and the question is as shown below:

The point to note is the splitting of the rational function into its partial fraction components. Once the LCM is sorted out, we can equate the numerators to get the values of the introduced unknowns as shown.

The video solution can be gotten here.

Differentiation from First Principles

Question 11a is on differentiation and we have a simple function to differentiate. But wait a minute. We are to use first principles! So go ahead and attempt this on your own.

I hope you really try this question out. Knowing the technique of differentiation from first principles is vital here. Once the formula is applied, e need to work at eliminating any stand-alone h in the denominator so that we will not have an undefined function while working. For questions like this, the more you practice, the better you become.

Watch the video solution from Davetuts Academy by clicking here.

Integration by substitution

Question 11b is based on integration but you need a little trick to solve it. All the best as you attempt this question.

Okay, the little trick is to use substitution. As you can see, trying to integrate straight will constitute the Herculean task of integrating the root of (1-x). So introducing another variable as a function of x and substituting appropriately is the way to go on this type of questions.

And the video is here for better understanding.

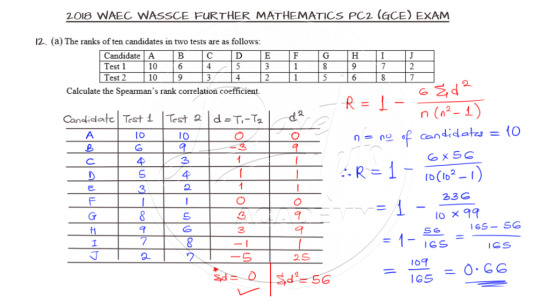
Finding the Spearman’s Rank Correlation Coefficient

Question 12a is on  Spearman’s Rank Correlation Coefficient and as expected, go ahead and lay your hands on this question.

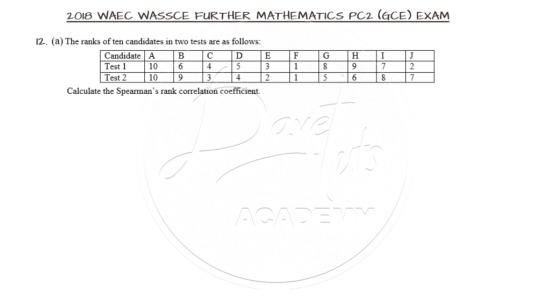
The Spearman's Rank Correlation Coefficient is used to summarize the strength and direction (negative or positive) of a relationship between two variables. For this question, we need to get the square of the difference in the two tests and use that in the formula for the Coefficient as shown below. As a guide, confirm that the sum of the differences equate to zero, otherwise, something is wrong with your calculation.

The video for the solution can be accessed here.

Evaluating Conditional Selection

A conditional selection is to be carried out in Question 12b and you can go ahead to attempt the question.

The first case is quite straightforward, but on the second instance, we need to apply our ingenuity to solve for that “harder” case as shown below.

Here is the video solution for the question.

Working with Binomial Probability 

Binomial Probability is featured in Question 13 for us to solve as shown.

Binomial probability refers to the probability of exactly x successes on n repeated trials in an experiment which has two possible outcomes. So here our possible outcomes from the selection is picking either a defective bolt or a non-defective bolt. The solution is as shown below:

Check the video tutorial for detailed explanation of the solution to the question.

Resolution of Concurrent Co-planar Forces

Question 14 is on the resolution of co-planar forces.

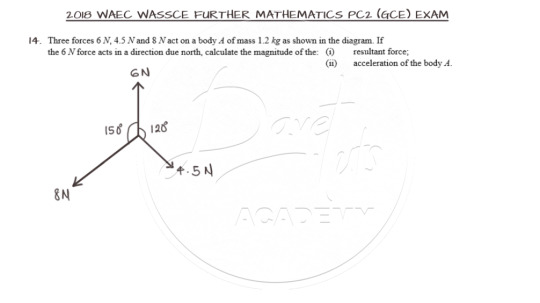
The solution warrants that the inclined forces be resolved to the horizontal and vertical components. This can be done in a variety of ways. You may prefer using the angles 150 and 120 degrees as given or the angles minus 90 degrees or as used in the solution, 180 minus the given angles. 

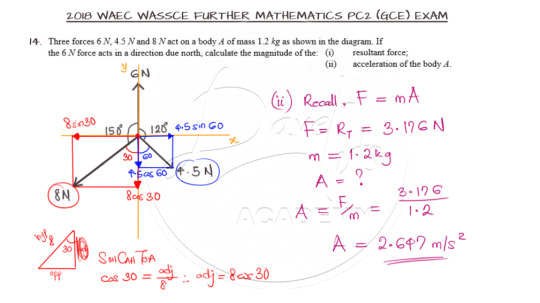
You can watch the video solution as shown below:

Final Velocity of a Stone under Free Fall

Question 14b features a free falling stone whose final velocity is to be determined.

The equation of motion comes in handy in solving the question as shown below

And here is the link to the video solution too.

Algebra of Vectors

Question 15a features the algebra of vectors. Go through and attempt the question on your own.

The solution involves opening the brackets and equating the components of the resulting vector equation to get the scalars as requested.

The video solution can be gotten here.

Parallelogram Law of Vectors

Finally, our last question features the parallelogram law of vectors.

The cosine rule comes in handy in solving this question and all you need to note is the requested angle as opposed to the angle used in the cosine rule. 

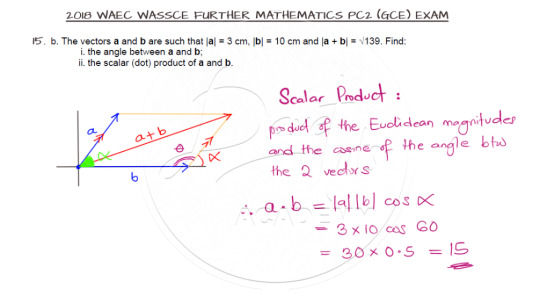
And here is the video solution:

So that is all about that.

Hopefully, you laid your hands on the questions first before checking with the solution featured here.

Kindly share this and let’s build academic excellence in students together.

Don’t forget to follow #davetutsacademy and visit our YouTube channel for more stuff like this by clicking here: Davetuts Academy.

[mathematicianadda]

Remedial College Algebra

We are all familiar with ‘predictions’ based on societal trends which are seldom validated by reality — whether it is flying cars, Facebook’s “population”, or economic stability.  Predictions are often based on a presumption of continuity within the determining forces; people attempt to apply modeling concepts to an open (or semi-open) system.  As mathematicians and mathematics educators, however, we often fail to notice the interaction between forces impacting our curriculum.

              At the collegiate level, the most dramatic example of such a disconnect is the course called “college algebra”.  I’ve written before about how ill-designed this course is, considering the role it plays; see College Algebra is Not Pre-Calculus, and Neither is Pre-calc, Cooked Carrots and College Algebra, College Algebra Must Die! and also about it’s history (see College Algebra … an Archeological Study. This post, however, deals with the conditions we are operating within in approximately the year 2019.

For reference, I will be using information about the Common Core Math Outcomes.  (See http://www.corestandards.org/Math/).  I recognize that the Common Core has many detractors, as well as structural problems within (such as insufficient guidance about which outcomes have a higher priority).  However, there is no dispute with this statement:

In spite of ‘problems’ with the Common Core, the Math Outcomes listed are the only usable reference for national conversations about K-14 mathematics.

So, here is the bottom line statement: if one compares the set of Common Core Math outcomes for K-12, they exceed the outcomes normally listed for a college algebra course required prior to pre-calculus.  Even the standard pre-calculus course is repeating content described in the Common Core.  [ACT conducts regular research on ‘national curriculum; the surveys are at http://www.act.org/content/act/en/research/reports/act-publications/national-curriculum-survey.html ]

Complex numbers?  Vectors? Matrices?  Connect zeros to factors? Binomial Theorem? Polynomial functions?  Rational functions?  Those, and more, are listed as Common Core outcomes for high school mathematics for ‘all students’.  I am not trying to equate the high school courses to a college algebra course; that is not a required element for the conclusion about college algebra as a course preceding pre-calculus:

College algebra is a remedial course.

The traditional remedial mathematics courses received that designation primarily because people saw that the content was what students SHOULD HAVE HAD in K-12 mathematics.  We maintained developmental mathematics courses which taught 9th to 11th grade mathematics, and denied college credit for them because students ‘should have already learned this stuff’.  [I am not suggesting that we allow remedial math to get credit towards a degree; in particular, I don’t think intermediate algebra should meet a math requirement.]

                      My claim is that the college algebra course preceding pre-calculus materially meets the same conditions which resulted in the determination that our traditional ‘dev math’ courses were remedial.  Substantially, every topic in the college algebra course should have already been learned in the K-12 experience.  Certainly, not every student had that opportunity (just as before).  Certainly, not every K-12 school does a quality job in mathematics (just as before) … though this statement also applies to “us” as college math professionals.

At the college level, we often function in isolation from K-12 mathematics; in general, we also continue to work as if the client disciplines exist now as they did 50 years ago.  We have not been sensitive to the dramatic changes in intent within the K-12 curriculum, and sometimes we seem to take pride in our ignorance of school mathematics.  We presume continuity as it relates to our curriculum, in contrast to our intense efforts to improve pedagogy.   I continue to believe something I have been saying for years:

Improving our pedagogy without modernizing our curriculum is like putting a GPS on a 1973 Ford Pinto — sure, we can see a map to help us drive, but it is still a 1973 Pinto.

We teach the importance of continuity within our courses.  I find it ironic (and tragic) that we tend to make basic assumptions concerning continuity within the world around us.  College algebra is a remedial math course.

  from Developmental Mathematics Revival! https://ift.tt/2CVAbuY from Blogger https://ift.tt/2Kxkm1I

[tutorsof]

Math Assignment-6

Question - 1

Write an equation in standard form of the parabola that has the same shape as the graph of f(x) = 3x2 or g(x) = -3x2, but with the given maximum or minimum. 

Maximum = 4 at x = -2

A. f(x) = 4(x + 6)2 - 4 

B. f(x) = -5(x + 8)2 + 1 

C. f(x) = 3(x + 7)2 - 7 

D. f(x) = -3(x + 2)2 + 4

Question - 2

All rational functions can be expressed as f(x) = p(x)/q(x), where p and q are __________ functions and q(x) ≠ 0.

A. horizontal asymptotes 

B. polynomial 

C. vertical asymptotes 

D. slant asymptotes

Question - 3

8 times a number subtracted from the squared of that number can be expressed as:

A. P(x) = x + 7x. 

B. P(x) = x2 - 8x.

C. P(x) = x - x. 

D. P(x) = x2+ 10x.

Question - 4

Use the Intermediate Value Theorem to show that each polynomial has a real zero between the given integers.

f(x) = 2x4 - 4x2 + 1; between -1 and 0

A. f(-1) = -0; f(0) = 2 

B. f(-1) = -1; f(0) = 1 

C. f(-1) = -2; f(0) = 0 

D. f(-1) = -5; f(0) = -3

Question - 5

"Y varies directly as the nth power of x" can be modeled by the equation:

A. y = kxn. 

B. y = kx/n. 

C. y = kx*n. 

D. y = knx.

Question - 6

Based on the synthetic division shown, the equation of the slant asymptote of f(x) = (3x2 - 7x + 5)/x – 4 is:

A. y = 3x + 5. 

B. y = 6x + 7. 

C. y = 2x - 5. 

D. y = 3x2 + 7.

Question - 7

Write an equation that expresses each relationship. Then solve the equation for y. 

x varies jointly as y and z

A. x = kz; y = x/k 

B. x = kyz; y = x/kz 

C. x = kzy; y = x/z 

D. x = ky/z; y = x/zk

Question - 8

Find the vertical asymptotes, if any, and the values of x corresponding to holes, if any, of the graph of the following rational function.

f(x) = x/x + 4

A. Vertical asymptote: x = -4; no holes 

B. Vertical asymptote: x = -4; holes at 3x 

C. Vertical asymptote: x = -4; holes at 2x 

D. Vertical asymptote: x = -4; holes at 4x

Question - 9

Find the x-intercepts. State whether the graph crosses the x-axis, or touches the x-axis and turns around, at each intercept.

 f(x) = x3 + 2x2 - x - 2

A. x = 2, x = 2, x = -1; f(x) touches the x-axis at each. 

B. x = -2, x = 2, x = -5; f(x) crosses the x-axis at each. 

C. x = -3, x = -4, x = 1; f(x) touches the x-axis at each. 

D. x = -2, x = 1, x = -1; f(x) crosses the x-axis at each

Question - 10

If f is a polynomial function of degree n, then the graph of f has at most __________ turning points.

A. n - 3 

B. n - f 

C. n - 1 

D. n + f

Question - 11

The difference between two numbers is 8. If one number is represented by x, the other number can be expressed as:

A. x - 5. 

B. x + 4. 

C. x - 8. 

D. x - x.

Question - 12

9x2 - 6x + 1 < 0

A. (-∞, -3) 

B. (-1, ∞) 

C. [2, 4) 

D. Ø

Question - 13

Solve the following polynomial inequality.

3x2 + 10x - 8 ≤ 0

A. [6, 1/3] 

B. [-4, 2/3] 

C. [-9, 4/5] 

D. [8, 2/7]

Question - 14

Write an equation in standard form of the parabola that has the same shape as the graph of f(x) = 3x2 or g(x) = -3x2, but with the given maximum or minimum.

Minimum = 0 at x = 11

A. f(x) = 6(x - 9) 

B. f(x) = 3(x - 11)2 

C. f(x) = 4(x + 10) 

D. f(x) = 3(x2 - 15)2

Question - 15

Write an equation in standard form of the parabola that has the same shape as the graph of f(x) = 2x2, but with the given point as the vertex (5, 3).

A. f(x) = (2x - 4) + 4 

B. f(x) = 2(2x + 8) + 3 

C. f(x) = 2(x - 5)2 + 3 

D. f(x) = 2(x + 3)2 + 3

Question - 16

Find the coordinates of the vertex for the parabola defined by the given quadratic function. 

f(x) = -2(x + 1)2 + 5

A. (-1, 5) 

B. (2, 10) 

C. (1, 10) 

D. (-3, 7)

Question - 17

Determine the degree and the leading coefficient of the polynomial function f(x) = -2x3 (x - 1)(x + 5).

A. 5; -2 

B. 7; -4 

C. 2; -5 

D. 1; -9

Question - 18

Use the Intermediate Value Theorem to show that each polynomial has a real zero between the given integers. 

f(x) = x3 - x - 1; between 1 and 2

A. f(1) = -1; f(2) = 5 

B. f(1) = -3; f(2) = 7 

C. f(1) = -1; f(2) = 3 

D. f(1) = 2; f(2) = 7

Question - 19

Find the vertical asymptotes, if any, and the values of x corresponding to holes, if any, of the graph of the following rational function.

g(x) = x + 3/x(x + 4)

A. Vertical asymptotes: x = 4, x = 0; holes at 3x 

B. Vertical asymptotes: x = -8, x = 0; holes at x + 4 

C. Vertical asymptotes: x = -4, x = 0; no holes 

D. Vertical asymptotes: x = 5, x = 0; holes at x – 3

Question - 20

The graph of f(x) = -x3 __________ to the left and __________ to the right.

A. rises; falls 

B. falls; falls 

C. falls; rises 

D. falls; falls