#Generalization of Logarithm product rule | Explore Tumblr posts and blogs

wejohannaballard-blog · 6 years ago

Text

Queue system - what do those stats really mean?

While comfortable waits would feel queue system shorter than uncomfortable waits. Providing information of waiting status to inform customers of their expected wait time, so as to signal the progress of the queue. Engaging the customers with activities such as entertainment and membership registration, so as to regulate customers’ perception of wait time. All these features would serve not only to queue system software managing customers’ image of a waiting line, but also to improve the customers’ perception of the service quality and the organization. Furthermore, according to previous studies, customers can be categorized into3 types based on their level of patience. These 3 types are attributed to various factors and demographic characteristics, such as age and past experiences. Within each type, customers’ level of patience varies differently as waiting time increases, which is as shown in Fig 6. The linear function represents how the group of standard customers would behave with waiting time theoretically.

While the logarithm function represents the group of less patient customers, who would tend to be more impatience very soon after the wait prolonged, and that the more patient group behave queue system software exponentially with waiting time. Undoubtedly that the latter group tends to have the highest level of tolerance towards waiting, so the ultimate goal in queue management is to simply optimize the queuing system and customers satisfaction, such that all customers would behave as the latter group, so that more customers more info would be willing to stay in line for longer period of time and thus in turns, maintain higher profitability of the organization. This framework and all of the other suggested design features are certainly not the most optimal solution to achieving this ultimate goal in queue management, there are certainly more aspect to be considered along with it, but it can definitely serve as the rules of thumb that provide guidance to successful management of queue, and ultimately, of service.

And with its general nature, this framework is made applicable to all real-life scenarios in a general sense. There are several limitations in this research study, which can serve as opportunities for future improvement and research: One limitation is the lack of controllability to both the subjects’ sampling and responses. The sampled subjects majorly falls within the age of 18-25 who come from Canada or China. This relatively narrow scope of the sampling did not allow accurate comparison of the queue preferences across various demographics. As well, due to the fact that the queue system singapore survey was conducted online, it was impossible to provide any clarifications when needed or control to incomplete entries, which would lead to unfinished surveys, and thus affecting overall performance of the survey results.

Due to fact that more than half of the interviewees are currently engineering students, who have slight knowledge of queues, they might be biased towards responding to the question being asked. A wider scope of interviewees should be sampled in future studies. Next step to the research could be enhancing the completeness of the framework developed, it should incorporate key design features of queuing system, which may include (a) number of servers, (b) number of lines, and (c) whether customers are processed comprehensively or sequentially by multiple servers. It should also incorporate additional factors click here that are related to the queue, such as (a) customers’ demand, and (b) types of products or services sold. Besides, another further development of the research would be testifying the framework using the operations research approach through incorporating the framework and key design features into the formulation of simulation models, which would essentially determine the most optimal queue system singapore set of queue design combinations. As well, these simulated models may also preserve the general nature, such that it can be customized to fit into different on real life scenarios by incorporating other relevant factors that are conditioned to the specific scenarios, such as capacity of waiting area, nature of product/services and customer demand. Finally, the customers’ degree to which they value waiting time as well as their temporal orientation should be considered in order to better understand the characteristics of the customers.

youtube

1 note · View note

tonkipie · 3 years ago

Text

Symbolic calculator wolfram

Symbolic calculator wolfram code#

If you have any questions or ideas for improvements to the Derivative Calculator, don't hesitate to write me an e-mail. The gesture control is implemented using Hammer.js. Complete documentation and usage examples. poles) are detected and treated specially. Wolfram Language function: Calculate the KullbackLeibler divergence between two distributions. For each function to be graphed, the calculator creates a JavaScript function, which is then evaluated in small steps in order to draw the graph. The interactive function graphs are computed in the browser and displayed within a canvas element (HTML5). Otherwise, a probabilistic algorithm is applied that evaluates and compares both functions at randomly chosen places. If it can be shown that the difference simplifies to zero, the task is solved. For example, this involves writing trigonometric/hyperbolic functions in their exponential forms. Their difference is computed and simplified as far as possible using Maxima. The "Check answer" feature has to solve the difficult task of determining whether two mathematical expressions are equivalent.

Symbolic calculator wolfram code#

For each calculated derivative, the LaTeX representations of the resulting mathematical expressions are tagged in the HTML code so that highlighting is possible. This, and general simplifications, is done by Maxima. For example, constant factors are pulled out of differentiation operations and sums are split up (sum rule). In each calculation step, one differentiation operation is carried out or rewritten. There is also a table of derivative functions for the trigonometric functions and the square root, logarithm and exponential function. The rules of differentiation (product rule, quotient rule, chain rule, …) have been implemented in JavaScript code. Instead, the derivatives have to be calculated manually step by step. It does not merely offer a convenient way to perform the computations students would have otherwise wanted to do by hand. The presence of such a powerful calculator can couple strongly to the type of mathematical reasoning students employ. Maxima's output is transformed to LaTeX again and is then presented to the user.ĭisplaying the steps of calculation is a bit more involved, because the Derivative Calculator can't completely depend on Maxima for this task. Symbolic calculators like Mathematica are becoming more commonplace among upper level physics students. Like any computer algebra system, it applies a number of rules to simplify the function and calculate the derivatives according to the commonly known differentiation rules. Wolfram alpha can give answers in simple cases, but from my experience ISC was much more useful. Maxima takes care of actually computing the derivative of the mathematical function. Inverse Symbolic Calculator (ISC for short) is down indefinitely (and has been down for many years). This time, the function gets transformed into a form that can be understood by the computer algebra system Maxima. When the "Go!" button is clicked, the Derivative Calculator sends the mathematical function and the settings (differentiation variable and order) to the server, where it is analyzed again. MathJax takes care of displaying it in the browser. This allows for quick feedback while typing by transforming the tree into LaTeX code. The parser is implemented in JavaScript, based on the Shunting-yard algorithm, and can run directly in the browser. The Derivative Calculator has to detect these cases and insert the multiplication sign. A specialty in mathematical expressions is that the multiplication sign can be left out sometimes, for example we write "5x" instead of "5*x". In doing this, the Derivative Calculator has to respect the order of operations. It transforms it into a form that is better understandable by a computer, namely a tree (see figure below). Linear algebra: matrix operations, determinant, rank, reduced echelon form, characteristic polynomial, etc.For those with a technical background, the following section explains how the Derivative Calculator works.įirst, a parser analyzes the mathematical function.Calculus: derivatives, integrals, limits, taylor expansion, etc.Algebra: operations on polynomials, such as expansion and factorization, collecting terms, division with remainder, etc.Store unlimited number of variables, create custom functions.5/15 is 1/3 and not 0.333 (unless you select rounded numerical mode) It offers all the advantages of an advanced graphing/scientific calculator mixed with the convenience of a modern mobile app. The perfect tool for students, teachers and engineers, built on an extremely powerful algebra engine, SymCalc solves any math problems from basic arithmetics to university-level advanced math.

#Symbolic calculator wolfram

0 notes

ikpress1 · 3 years ago

Text

TEACHING AND LEARNING LAWS OF LOGARITHMS: A PROSPECTIVE PEDAGOGY | Journal of Global Research in Education and Social Science

According to the literature, pupils have a rudimentary comprehension of the laws of logarithms, including misunderstandings. Despite the fact that these rules are critical in learning advanced mathematics, this is the case. The difficulty in acquiring these concepts is largely related with rule-based teaching, which fosters rote learning and is not supported by learning psychology, according to this research, which is based on teaching experience, textbook analysis, and classroom observation. A guided inquiry oriented, ICT enhanced, investigative pedagogy is presented to address challenges with product, quotient, and power norms. Students will work in small groups to analyse both accepted and unanticipated (misconceptions) log rule equations side by side. They create their own data by plotting 3D graphs of the above equations and solving them. They are then advised to examine similarities and differences in the ranges of the equations data to pick the most acceptable and general log rule equations by testing their self-generated and teacher-provided data. This method is assessed using learning theories, and it is backed up by constructivism and neurocognition. This approach is recommended for future investigation into smart teaching and learning, given the stated benefits for teaching laws of logarithms. Please see the link :- https://www.ikprress.org/index.php/JOGRESS/article/view/1800

#Mathematics #laws of logarithms #misconceptions #ICT #guided discovery

0 notes

drunk-math · 7 years ago

Text

Let'sh shay there ain't no 'nfinny!

Imagine there's no heaven, it's easy if you try... take a look at Carathéodory's notion of entropy and it'll tell you something about the nature of consciousness. Anyway.

Onto the greatest bugaboo of mathematics, infinity. Essentially, in the universe, there's no such thing as infinity, and yet so much mathematics today is about the various subtleties of it. Consider in particular the infamous axiom of choice - if all sets are finite, then the axiom of choice is trivial. Of course it's ridiculous to believe that all sets are finite, as ridiculous as it is to believe that the set of all sets does or does not contain itself.

So consider two paradoxes, Russell's and Galileo's. Galileo who's worshipped by proddies for poking the holy bear (...well, I guess the holy bear per se'd be further East) until he bit came up with the mindblowing paradox that there are infinite even numbers and infinite odd numbers, and came to the conclusion that the notions of greater than and less than make no sense for infinite sets. Should've been left there, but someone had to cant his diagonal Canticle over Canticles and make manifest the notion of multiple infinities and therefore of infinite sets.

"But wait!" you say, "weren't there always infinite sets? What about Euclid's proof that the primes were infinite? Hell, what about the very notion of natural number?" Well, yes, but are those sets? That's where Russell's paradox comes in. The notion of a set as "a bunch of shit" doesn't work, because then you could have all the shit that doesn't have its own shit, which both does and doesn't have its own shit. (Incidentally, while the doctor was a woman - both large and small D going into 2018 - the barber was definitely a man. Making the barber a woman misses the point.) Although... actually, maybe the barber sort of is a woman? Maybe.

Basically, what I'm saying is woman = class. And the first thing you need to know about classes, i.e., women, is that they don't exist. I mean, nothing in math quite exists, but these especially don't exist, and their nonexistence is critical to understanding them. These objects, such as the universe of discourse, are not in the universe of discourse, and therefore can't be discussed. What's the universe of discourse? It'd be the set of all sets, but that doesn't exist, so it's the class of all sets, which also doesn't exist, and since it doesn't exist, it's a class.

Why doesn't it exist? Because the only way you can make sense of sets is by saying that, for any set and coherently expressed property, if you have a set, you have a subset consisting of those elements that have that property (even if there aren't any, in which case it's the empty set, and that's fine). If the property is not containing itself, then the set of all sets would have that property iff it didn't have that property. That's Russell's paradox, and that means that a distinction has to be made between sets, which do exist, and classes, which don't. In particular, you cannot be allowed to make the statement, even in the negative, "this class is a member of..."

So why should infinite sets be allowed? Be rid of the axiom of choice and the axiom of infinity; replace the latter with an axiom of finiteness and an axiom of empty set. This will give you Peano arithmetic, and it will make the notion of countability nonsense. What Cantor diagonals would reveal has already been revealed by Galileo. But then what about sets on the real line? Because even restricted to rationals, let alone proper superclasses, that would fail the axiom of finiteness.

So how to define finiteness? The normal definition involves a bijection with a cardinal set, the normal definition of which (a sort of canonical set of a given natural size) essentially is the axiom of infinity, so that's right out. Easiest to axiomatize would be Tarski finiteness, which means that, given a set and a set of subsets of that set such that for every pair of elements one contains the other, then one of those elements is contained in no other. (I'm really tempted to try to write that in symbolic language, but I will have behaved myself so well so far.) Normally, this doesn't imply finiteness in the first sense without the axiom of choice (which is obviously right out), but ZF alone - without infinity or regularity - is enough to show it implies Dedekind finiteness (no proper subset has a surjection onto the whole set, or equivalently, no subset has a bijection to the natural numbers), and that Dedekind finiteness of the set of subsets of the set of subsets is enough to imply natural-number finiteness; therefore, if every set is Tarski finite, then the power set of the power set stupid double subset thing I just mentioned of a given set must be Tarski finite, and therefore Dedekind finite, so every set is natural-number finite. (The definition of the natural numbers - which don't comprise a set - will be a bit ad hoc.)

(This is where that entire Banach-Tarski rant from the last post went.)

Of course the theme of this post gets rid of that paradox, so forget the entire last paragraph. In fact, it collapses any number of paradoxes into what amount to one mega-paradox with fewer metamathematical consequences. I don't know what those are, but what they are they really aren't, are they? After all, the probability of the destruction of mathematics is impossible to assess (any truly rigorous definition of the set of definable numbers would do it - although there are many contingent ones, even contingent ones that can be without contradiction established by fiat to be, per Skolem's paradox - but that lies behind a wall of universal Skolemization) - and perhaps all probabilities are impossible to assess, with such a recasting of set theory. I'm not the first person to suggest this - Kronecker being the most celebrated - although perhaps the first so incoherently (I expect this post, indeed, the entirety of this blog, is just the right combination of informed and erroneous to be infuriating to every level of mathematical acumen), and there are untold hurdles, one of which I've just mentioned. So let's go back to that thing I harp on all the time - PNT. Let's build from the ground up, sort of, in an unholy fusion of Euclidean geometry and set theory applied to modern analysis and number theory. That might be getting me where I'm going. The Lebesgue integral certainly relies on infinite sets as a part of measure theory, so best to stick with the Riemann.

Of course, that brings up the notion of how to define limit. In ZF, it's impossible to prove without countable choice that the epsilon-delta definition of limit is equivalent to the existence of a sequence that comes to the limit in question. In this universe, the latter definition is incoherent, since no infinite sequence exists at all. The former can be restricted harmlessly to the rational numbers, which raises the question of what exactly the limit is; the limit is the rule, which is finite. Similarly, the twofold - two is less than infinity ("less than" expressed as an ordering of the set of cardinalities with at least one infinite cardinality as an element) - composition of limits (one of those limits being a series) in the definition of the integral is a composition of rules. (This computational approach makes me essentially the set-theoretic equivalent of the "nullity" guy, by the way. Well, that's not fair; he got better grades.)

Now, recall the "evidence." Now, it might seem shocking to try to work with the Euler product, in either form, without infinite sets (the reals themselves - Dedekind cuts - are infinite sets), but an infinite sequence, speaking informally, need not imply an infinite set, as long as the rule is finite. What's generated, then, provided the series is convergent, is a Dedekind cut, which would be a proper class under the axiom of Tarski finiteness. However, that's not really important, but rather, what's important is the rule, and manipulations of this rule under the arithmetic operations by a sort of composition; a rigorous definition not found in this post would most likely come from the theory of computation.

I remember how much easier I found vector calc than I did linear algebra. This was because in vector calc, I had already guessed most of the basic operations from simply generalizing the rules from one-dimensional high school calculus. At that age, I couldn't wrap my head around the fact that this clearly wasn't enough. To some extent, modern set theory's treatment of analysis is a formalization of this misapprehension, so that it ceases to be a misapprehension. Let's take the alternative perspective, Turing standing on Peano's shoulders rather than Zermelo's for the hypercomputability hierarchy to replace Gödel's. Let's enhance our confusion to create a grand certainty.

Back to the point. To recap, the "evidence" is that if you take the logarithmic derivative of the zeta function you get the logarithm of each prime in turn divided by one minus that prime to the negation of the parameter, which can alternatively be expressed, per Euclid, as the logarithm of that prime multiplied by the sum from zero to infinity of one over the powers of the prime in question to the parameter (remember, though, that this is a finite rule as opposed to an infinite set). Considering that, all terms being positive, this converges absolutely, the terms can be rearranged; note that the terms that are generated by the rule are exactly fractions with prime powers raised to the parameter in the denominator with the log of the base in the numerator, so let's put them in the order of the prime powers.

Before we go on l let's go back to that sentence, "considering that this converges absolutely, the terms can be rearranged." Remember when we all learned that in high school? But the concept of a permutation on an infinite set is taken as read there, so it's imperative to prove the equivalent principle again in this new framework. By the definition of limit, we can always run the partial long enough that it'll be within some given distance of the sum. In that, provided we have some idea where the terms are going, there must be a maximum destination, which must be equal or greater. Therefore, it must include all the terms, and more. If they're all positive, then this can only be larger. Therefore, it's true of the absolute value. Term-by-term summation following from that of the partials and the arbitrarily low upper bound on the tail, you get from there and the convergence of a subseries to the case of absolute convergence.

Anyway, back to the "evidence." From here it's pretty clear. You can make this sum by layering up integrals that start at each prime power, which will each be the parameter times the log (when there is one) divided by the index to the power of the parameter plus one. So moving the sum inside the integral (since it's absolutely convergent - same argument as before, only this time with Riemann sums slid in) you'll get the second Chebyshev function divided by the parameter of the integral to the power of one plus the parameter of the zeta function, all multiplied by the parameter of the zeta function. If you plug in one, the derivative of the log of the zeta function blows up, and so this integral blows up as well - which is what you'd expect if the second Chebyshev function asymptotically approached identity, because then you'd be dividing identity by the square to get the reciprocal so that would blow up. You'd also expect, then, that subtracting the reciprocal would cause it not to blow up, and in fact this would imply the asymptotic approach. The suggestion of this comes from the fact that if you multiply the zeta function in the log by one less than the parameter, the derivative manifestly converges.

So that's the "evidence," but it's not the proof because we can't obviously move the limit inside, not even with the normal machinery of set theory/analysis. So why can we move the limit inside? The short and incoherent answer is because there are no zeroes on the edge of the critical strip. The proof of this I won't restate - it's just algebra and trig - but the connection still isn't inherently obvious. From there, what's left is the Wiener-Ikehara theorem, which it's even more imperative to view now in terms of Fourier analysis, that is to say, constructing a function from an uncountable accumulation of sinusoids. Might be some kinks to work out there in the absence of infinite sets.

So basically, as I said before, the actual proof is based on the notion of an "approximation of unity," a family of functions of integral one that approach zero bar an infinite isolated point. (Again, none of these concepts exist, but speaking in shorthand, that's what it is.) Multiplying this by offsets of another function allow you to show that that function approaches a constant, and in this case to show that the second Chebyshev function approaches the identity. The fact that this approaches a limit comes from the equation discussed before.

Now, so far, I'm just drunkenly ruminating on cud already so thoroughly chewed. What's interesting, though, is that not only are all these limits determined by finite rules, but that they themselves are their solutions, and these rules for arithmetic operations axiom schemata, rather than inferences. The question, then, isn't whether they follow, but whether they're eliminable in whatever context is important to our purposes. And that's what brings us back to Euclid.

Remember, the challenge there is to build from the sparse postulates of his geometry and "number theory," to which not even he can hold himself entirely, to get to such a radical conclusion regarding the prime numbers. In his terms, as before, it can be expressed only in terms of the harmonic series - at least without great difficulty. New chapters might be introduced bringing it to modern terms (i.e., at the very least, terms in which RH in prime-number form would be meaningful) without a modern notion of infinity, but these would be lengthy chapters. For now, let's go with the prime counting function and the harmonic series. I said then that we would need definite error bounds, but let's replace that with "as close as we like."

Let's work backwards. We first need to start with the fact that an increasing (non-strictly) function that's convergent when you add it up (at integers because no infinity - note that this is an integral of a function of countable range in the ordinary paradigm) subtracting identity and dividing by the square must approach in ratio identity. This follows from the divergence of the harmonic series in effect - if it didn't approach identity in ratio, then the ratio would either approach a number greater or less than one, or it would diverge, being unable to oscillate due to the function's monotonicity. If it did those things, the function wouldn't converge.

From there, two things remain to get us to "as close as we like." If only I could remember what they were. (I suppose I should mention on this point that my hippocampus is a pickled seahorse on a toothpick.) I suspect they're to show that the increasiness is finite for positive parameters and that it reflects the limit. The former is easy enough to show from series (to wit, by saying that it holds for any power, however small, the concept being expressed easily enough geometrically), the latter coming from Fourier analysis. In any case, really, there's no real logic to this other than what I mentioned before, only the relevance of it to this notion of mathematics without infinite sets.

So let's not fuck around. Fourier analysis, the analysis of periodic functions on the real line expressed as the integral of an uncountable set of sine waves, without infinite sets. How? Well, not at all, really, but basically by geometry, obviously. Sine waves, after all, come from sines, the string of a bow the chord, the musical sense of "chord" after all coming from the chord a string made against a lyre (as far as you know), and Euclid knew the law of cosines in a geometric, very Alexandrian form (propositions twelve and thirteen of book II).

So let's go back to the very beginning of this blog. The normal distribution. Now, the slovenly proof I gave then doesn't really show anything and isn't the normal (so to speak) approach anyway. A better notion of probability comes through set theory and measure theory, the latter of which certainly doesn't work as normally understood in a finitist paradigm.

So you'll remember I explained (ish) why a series of fair coinflips should approach the standard normal, but I didn't explain probability beyond that at all. So what is probability? Well, you take a set, a subset of that set's power set closed under complementation (relative to the base set) and countable union, and a function from the latter to [0, 1] such that the empty set maps to zero, the union of countable disjoint sets maps to the sum of those sets' image (implying the union of countable non-disjoint sets is less than or equal to the sum of those sets' image), and the whole shebang maps to one. That's a probability space. Now, if the set has to be finite, you're golden to model, e.g., cards or dice, but you're SOL if you want to model a dartboard, unless you feel like working it out at the quantum level, but even there there may or may not be infinities where probability is concerned. Therefore, under this paradigm, the base set and space would have to be understood in terms of the rules that generate them - but aren't they anyway?

So with that in mind, the notion of approaching a probability space via a series of fair coinflips is analogous to the notion of approaching a real, computable or uncomputable, by a Turing-equivalent machine. Now, I didn't bring up Turing machines (exactly) above because even in this paradigm uncomputable numbers can be defined, such as the sum of two to the power of the negations of successive busy beaver numbers.

I've been writing this for months now, and I'm sure it's wicked self-contradictory and flows like tar, but fuck it, it's going up.

#infinity #set theory #probability #gambling #computability #prime number theorem

3 notes · View notes

allenmendezsr · 4 years ago

Text

Trend Sigma

New Post has been published on https://autotraffixpro.app/allenmendezsr/trend-sigma/

Trend Sigma

Buy Now

During its steep ascent the price of Hansen Natural’s stock got multiplied by a factor of about 100 in a matter of only 3 years. This is of course hindsight and I presented on purpose an impressive example, but the chart demonstrates something.

It shows directly that you could have made hundredfold back of what you invested. Stocks often have large moves, much bigger than the ones of commodities or currencies. But at risk would have been only the investment itself. This asymmetry clearly favors stocks over all other financial instruments. Their leverage is no compensation for the asymmetric price behavior the stock investor enjoys. Trading on margin with Forex or futures can let the account go below zero, which is simply a linear and not a logarithmic growth behavior. Options have a premium that decreases over time, which destroys the advantage their non-linear pricing pretends to offer at a first glance.

But there is something else. The multiplying happened with a trend that went straight up and was almost always at its current high. In such a situation the market forces that are playing against the small trader are diminished….

Most traders, and investors even more, are not aware that a price at the high is a different situation than a price elsewhere. Generally, it is a signal for more of the same to come and not for a retreat, as it may look to so many. It is an exceptional situation, indicating that there is a force hindering the price to swing back, which it normally would do.

Still, trading is what it used to be, a statistical game. There are situations near the high where the odds are skewed to your favor, but you must be able to identify them and to behave methodically. In other words, to exploit this exception, a trading system is necessary.

What characterizes this trading system?

Possibly interested in this system could be trend followers and swing traders, but also investors who want to pursue a more active approach in the market. It may be also valuable for day traders, even if they are not willing to use the longer-term components of the system. But who knows, perhaps one or the other of them will finally find out where the real money is.

Why is this trading system interesting?

The whole stock universe is screened by selection criteria for companies with the right product coupled with long-term price strength of their stocks. The fundamental growth situation of a company that is caused by its special product is something which likely has an ongoing momentum. Together with a confirming price strength this is the best possible indicator for an enduring trend. Consequently this process will find the gems that have the greatest future potential. There is a set of simple rules accompanied by three groups of buy setups and another set of sell signals. This rigid structure enables a daily bar oriented trading style. There are situations where intraday charts may be used, but the emphasis lies on trading the daily bar chart and you can ignore completely any information with a shorter-term horizon. This rule-based trend trading system tries to achieve efficiency with simplicity. Both points above suggest that this is the modern version of Nicolas Darvas’ famous “techno-fundamental” trading system. However, its entry system is much more elaborated to be better adapted to modern market behavior. The selection of trading candidates is also more sophisticated. Darvas entered a stock only at its absolute high, something that proves to be a real constraint. If, for instance, the whole market is weak, this method allows to trade on relative strength alone far from the actual high. There are other differences like money management. Darvas essentially had none, as he grossly over-traded back then. But luck was with him, as he started directly at the beginning of a bull market. This trading system could be viewed as the successor of the Darvas method. Major parts of it, like the entry rules, got replaced completely and all in all it is much more refined as a system. A necessary part of any trading system is sound money management. This system maximizes the long-term performance and keeps the principal risks in check. Simply diversifying into many stocks is not the answer, because that would dilute not only the single failure but also the single gain away. Instead, using the right borderlines, knowing what you can do and what not, is the key. While money management principles have to work on their own as a final safety net, this system supports them with strong help from the trading side. Some of the trading rules represent a stiff stop-loss system. This is a semi-automated system that tries to beat completely mechanical ones. There is a frame of precise rules that incorporate the “tricks” of trading at the high, but there is also the trader. For that reason one whole chapter is devoted to psychology, including a comprehensive list of what can possibly go wrong with solutions or at least ideas to get on the right track. Ideally this trading system enables its followers to earn with a modest amount of work a maximum of return. Does it make sense to hope for big gains with trading slow moving stocks, dull stocks of dull companies or even slower moving currencies? Or to do the opposite and chase tiny intraday movements with an exhausting maximum of concentration? Is it wise to invest in stocks that fell back and hope that there was no sufficient reason for their fall? I don’t say that there are no other ways to trade, but in my opinion the best possible thing to do is to invest in the best trends there are.

Trade the best trends there are. As Darvas put it more than 50 years ago:

“There was nothing else for me to do while Texas Instruments, Zenith Radio and Fairchild Camera went to work for me”.

This trading system is available as an eBook, which is written in a focused style and aims to be a thorough explanation of the system and a manual or checklist for day-to-day use. I don’t repeat much, if anything, and I don’t start with the basics. You should have already at least some trading experience. Any successful trading system requires a user willing to invest some work into understanding and executing it. This trading system can lead to outstanding results, but it is not the magic formula that makes everyone rich by producing infallible buy and sell signals. If you have already traded, you know that there is no such thing. It also should be clear that it can’t exist for logical reasons.

The eBook has almost 120 pages and comes as a digital product, namely a PDF file, which can be viewed with any modern PDF reader like the one from Adobe. You can also print it out or read it with accessibility tools.

Interest in fast moving stocks is an indicator that this system is right for you. If you are a convinced value investor, it may only suit you if you are willing to experiment. Of course, you are welcome to try it.

Many investors changed successfully their trading mind. As I mentioned before, if you like Forex, futures or options more than stocks,

I strongly urge you to do so anyway.

In case you want to have this system, you can get it right now. Immediately after your buy, which is securely processed by Clickbank, you will get your personal download link from where you can download the eBook. There will be an email address for possible download problems. Clickbank has also a 60-day return policy and processes all refunding requests. So you can rest assured that you are exploring an investment with some intrinsic security right now.

Why does the system work?

Stock Trading System

“a profitable investment”

Make the right investment now and transform yourself into a successful investotrader.

T. Silverstone

P.S. If you are hesitating, read this: Why Trend Sigma

0 notes

laceyspencer · 4 years ago

Text

Acquired Goodwill and Residual Income Components: A Study on the French Market-Juniper Publishers

Introduction

The goodwill is the discounted sum of future residual income, i.e. earnings beyond the “normal” return on capital and called abnormal or extraordinary earnings [2]. Under IFRS 3 Business combinations, goodwill arising in a business combination represents a payment made by the acquirer in anticipation of future economic benefits from assets that cannot be separately identified and recognized. Only acquired goodwill is accounted for under IFRS. Internally generated goodwill is not recognized as an asset because it is not an identifiable resource controlled by the entity that can be measured reliably at cost. The rules applicable to the recognition of goodwill in the consolidated accounts of French firms were largely modified by the adoption of IFRS on 2005. Hence, with the removal of systematic depreciation of goodwill and its replacement with impairment testing, return on equity of listed companies instantly increase.

This study focuses on French firms composing the SBF 120 (Société des bourses françaises). It seeks to establish the extent to which goodwill in a given period generates consecutive residual income, according to two components: net income and other comprehensive income - OCI. Moreover, confirming the link between the acquired goodwill and subsequent residual income pave the way for empirical research highlighting the periods or areas where goodwill is justified or otherwise where the price premium is obvious.

Future residual income of the target firm and synergies are the heart of goodwill (core goodwill) and are the only elements that deserve to be capitalized as goodwill. Henning et al. [3]. show a positive and statistically significant association between stock returns and these components, with a greater weight for synergies. However, the premium paid would be negatively valued by the stock markets, seen as an additional cost of the combination.

Goodwill and Future Residual Income

It is known at least since Preinreich [4] that it is possible to assess the market value of equity of a firm from its shareholders’ equity and the sum of its residual abnormal or future earnings; the discounted sum of the latter constituting the economic goodwill. This relation is formalized in the Residual Income Valuation model [2,5] obtained using the residual income defined from clean surplus relation (i.e. comprehensive income). Since, there has been debate as to whether transitory or unrealised items constituting OCI are relevant [6,7].

Let’s decompose the price paid for the acquisition of firm i at time t as the market value of equity pi.t over Syni the present value of expected synergies from the transaction plus a premium SPi linked to hubris’ leaders, at a pricing error, at market conditions, negotiating conditions or strategic premium. Starting with residual income valuation:

p = Market price, bv = book value of equity, xa = Residual income

(2) Price paidi.t = pi.t + SYNi + SPi where SYN = Synergy, SP = Stock premium

pi.t is replaced in (2) by expression in (1):

Then replace Price paidi.t in the definition of goodwill (3):

(3) Goodwilli.t = Price paidi.t – FVEi.t where FVE = Fair value of equity

Upon acquisition, FVE = bv

The goodwill recorded for firm i in t is equal to the price paid, less the fair value of its equity (FVE).

Empirical Model

At the acquiror level, successive acquisitions generate in times goodwill, and hopefully residual income and synergies, i.e. residual income for the buyer. We separate residual income into two components, and control for market value and P/E.

: Market value of equity. These variables are scaled by equity book value in year t. P/Et: Median Price-Earnings ratio in year t.

Comprehensive income (CI) is computed as the variation of equity net of transactions with shareholders. Items are: Ordinary Share Capital, Preference Capital Reserves, Equity Issued and Dividends Paid [8].

The cost of equity rn is computed by applying the CAPM as the sum of risk-free rate (annual) and the product of an equity risk premium (fixed) by beta (annual). The financial data - Treasury bond rate (OAT 5 years) and betas were also collected annually on Datastream. The equity risk premium has been fixed at 4%. Goodwill and total intangible assets are collected from annual reports.

An implicit assumption is that the subsequent residual income is representative of all earnings generated by an acquisition in the medium to long-term. Statistically, this assumption is realistic for a large sample, although at the firm level, we can always highlight growth patterns of nonlinear earnings. In addition, this point is in line with the assumption of autoregressive process or persistence of residual income of Ohlson’s model.

We can capture the series of all residual income through market capitalization divided by shareholders’ equity. Dividing the terms of the residual income valuation (RIV) by book value of equity, the Market-to-Book ratio then appears to be equal to 1 plus the sum of future earnings anticipated by the market and divided by equity. The Market-to-Book ratio captures earnings generated over a long period, including goodwill and other capitalized intangible assets. By using the Market-to-Book ratio as the dependent variable, Cazavan-Jeny [9] had already highlighted on pre-IFRS French data the significant association of goodwill divided by total assets. The integration in the regression of Market–to-Book is in line with the assumption of autoregressive process or persistence of residual income. It is expected that the market to book ratio is strongly correlated with the residual outcome measures, generating multicollinearity.

Concerning the proxy for stock premium, we use the median ratio on the sample Price-Earnings ratio. As in Gu & Lev [10], P/E captures for each year fluctuations in the equity markets affecting the price of acquisitions. We must also keep in mind that the value relevance studies show a positive association between goodwill per share and stock price.

Sample Selection

This study focuses on 71 non-financial firms listed in the French market index SBF 120 for years 2005 and 2008, representing a sample of 284 firms-years. The sample starts from 111 nonfinancial firms from which we remove 11 firms with no goodwill or negative equity. From this sample of 100 firms, we focus on observations presenting high external growth as expressed by a ratio of Goodwill/Total intangible assets larger than 50%.

Results

(Table 1) presents descriptive statistics to all the variables. Other comprehensive residual income component on average represents 4% of equity against 6% for net residual income component. Goodwill and total intangible assets represent on average 69% and 106% of equity respectively.

(Table 2) reports results of hierarchical regressions on the determinants of goodwill. Since we use panel data to estimate our models, the problem of heteroscedasticity and autocorrelation might be an issue. The test of Breusch-Pagan/Cook-Weisberg shows the presence of heteroscedasticity. Thus, the structure of errors among the panels is presumed to be heteroscedastic. To this end, we estimate regressions by the method of feasible generalized least squares (FGLS) with random effects (based on Hausman test). To overcome the problems of stability of regressions that generates the correlation between residual income and Marketto- Book, we use the natural logarithm of the Market-to-Book ratio. Results are the following. First, the successive introduction of variables is done without disruption of coefficients and progression of Wald test for each coefficient introduced. We observe that future residual net income has a larger influence on goodwill than future other components of comprehensive residual income (xa n - x* n) (coefficient of 0.41 versus 0.19 in the last two columns). The coefficient carried by the logarithm of the Marketto- Book is very significant and with a consequent value despite the use of the logarithm. The coefficient carried by the P/E median has the expected sign but is not significant at conventional level. However, the wald test increases with the addition of this variable in the regression.

Residual income arises not only from acquired goodwill but also internally generated goodwill. Therefore, as a second specification, we replace goodwill by total intangible assets as the dependent variable. The coefficient on the variable xa n - x* n is negative and of low or no significance, whereas the coefficient on x* n is positive and significant. It is not surprising since there is no connection between marks or patents capitalized on the balance sheet and the unrealized gains on investment securities or foreign currency translation adjustments; components of OCI.

Conclusion

We formalized, from the Ohlson RIV model, a theoretical link between acquired goodwill of listed companies and their subsequent residual income; by breaking down the purchase price and goodwill acquired as Johnson & Petrone [1]. Empirical test of this relation was intended to test three estimators of future earnings:

a) The residual comprehensive income,

b) Broken down into residual income and

c) Additional residual income and the ratio of market-to-book.

Results are the following. First, the relationship between the acquired goodwill and subsequent residual income is very strong, on the net income component, which variations appear as the key to judge the quality of the acquisitions. Second, the residual net income component carries positive coefficients and higher than the additional component (other comprehensive income - OCI). Third, coefficients carried by OCI component are significant and approaching half the value of the coefficients of residual earnings, reflecting the interest of that information for assessing external growth; it is the main contribution of this article, i.e. showing the benefits of reporting OCI. Finally, acquired goodwill and Marketto- Book ratio are positively and highly associated, suggesting that the accounting measure of acquired goodwill is informative for the market.

The original contributions of this research can be summarized as follows:

a) To our knowledge, this is the first study to gather the Residual Income Valuation and the analytical breakdown of acquired goodwill, to formalize a link between the latter and the consecutive residual incomes of the transaction for the purchaser;

b) Consequently, it is also the first study to empirically estimate this link, taking as estimator the residual income of the purchaser;

The breakdown into two segments, net residual income and additional residual income, highlights some usefulness of OCIs (Other Comprehensive Income), which appear posteriori statistically associated with acquired goodwill, thus as having participated in the formation of transaction prices.

https://juniperpublishers.com/asm/ASM.MS.ID.555616.php

For More Articles in Annals of Social Sciences & Management studies Please Click on: https://juniperpublishers.com/asm/index.php For More Open Access Journals In Juniper Publishers Please Click on: https://juniperpublishers.com/index.php

#Juniper Publishers #open access journals #Social Sciences #Goodwill #Residual Income #Ohlson’s Model #Management Studies

0 notes

fractalcult · 7 years ago

Text

Market Myths: Good, Bad, and Bazaar

The stories that hold up western* capitalism

First, a procedural note…

The truth value of a myth doesn’t matter, where efficacy is concerned. However, some myths have become so strongly internalized that they become difficult to identify as myths; they are mistaken for “common sense”. For most of us, the ideas underlying western* capitalism are like this. It’s difficult to separate ourselves from these myths and gain the appropriate distance, so I’m going to engage in a little bit of ‘debunking’ — specifically, I’m going to take some time pointing out parts of the capitalist model that don’t match with reality or history, during the course of analyzing its structure and function. This doesn’t take away from the immense power and importance of capitalist mythology, nor does it indicate that I consider all of the ideas associated with capitalism to be strictly false.

On tautology

Academics tend to treat tautologies as a lesser form. Tautologies are shallow, by their nature. It’s quite reasonable for a system optimizing for novel and interesting ideas to reject tautologies. Nevertheless, some really important ideas can be rephrased as tautologies — as Charles Fort points out, natural selection is better summarized as “survival of the survivors” than “survival of the fittest” — and one can make the argument that any really true argument is in some sense circular. There’s no shame in a circular argument that depends only on true premises. In fact, this is one way to look at all of mathematics — which is true because of its internal consistency, and only accidentally coincides with physical reality.

When someone dismisses a seemingly profound statement as “just a tautology” they omit important information. An obvious tautology contains no information. However, a non-obvious tautology is just about the most profound thing imaginable — it takes a complex, incomplete, vague collection of loosely related ideas and replaces it with a much smaller and simpler set of rules, which (if the tautology is reasonably close to correct) is both at least as accurate as the original set of ideas and easier to reason about. A non-obvious true tautology refactors huge sections of our mental models. Obviousness is a function of existing knowledge, so what is an obvious tautology to some people will be non-obvious to others. It should come as no surprise that people seek out ideas that present themselves as non-obvious tautologies.

The drive toward seeking non-obvious tautologies can lead to mistakes. Looking for simple and efficient models of the world is a mechanism for enabling lazy thinking. When lazy thinking is correct it’s strictly superior to difficult thinking, but lazy thinking often comes with lazy meta-cognition. If we jump on ideas that look like non-obvious tautologies too greedily, we fail to see hidden assumptions.

Market efficiency is a very attractive model. Under certain circumstances, we can expect things to actually work that way. If a large number of competing producers really do start off completely even in capability, we really can expect the Most Unexceptional product to price ratio to win out. To accept it completely means ignoring hidden assumptions that serious thinkers should at least consider.

One hidden assumption in market efficiency is that competitors start off even in capability. This is almost never the case outside of a classroom demonstration. Companies enter established markets and compete with established competitors, and companies established in one market will enter another. Both of these mechanisms make use of existing resource inequality in order to reduce precisely the kinds of risks that lead to efficient markets, and while perhaps in the long run poor products might lose out, with the extreme spread of resource availability the “long run” can easily last until long after we are all dead. Given no other information, if age is not normally or logarithmically distributed, we can reasonably expect something to last about twice as long as it already has. With corporations, the tails of this distribution are further apart — we can expect a startup to be on its last legs, and we can expect a 50 year old company to last 75 more years, because resource accumulation corrects for risks. A company that has a great deal of early success can coast on that success for a much longer period of poor customer satisfaction.

Another hidden assumption is that communication is free within the set of consumers and between consumers and producers but not within the set of producers.

Free communication within the set of producers is called collusion, and the SEC will hit you with an antitrust suit if you are found to engage in it. People do it all the time, and it is usually worth the risk, since it reduces market efficiency down to almost zero.

Free communication between producers and consumers is also pretty rare: even failing producers typically have too many consumers to manage individually and must work with lossy and biased aggregate information; successful producers have enough resources to be capable of ignoring consumer demand for quite a while, and often encourage ‘customer loyalty’ via branding. (In other words, cultivating a livestock of people who will buy their products regardless of quality — ideally enough to provide sufficient resources that appealing to the rest of the customers is unnecessary). Customer loyalty can have its benefits compounded if wealthy customers are targeted: “luxury brands” are lucrative because something can be sold well above market price regardless of its actual quality or desirability, and sometimes the poor price/desirability ratio is actually the point (as a form of lekking / conspicuous consumption).

Free communication between consumers is becoming more and more rare, since flooding consumer information channels with fake reviews and native advertising is cheap and easy. There used to be stronger social and economic incentives to clearly differentiate advertising from word of mouth, but advertising’s effectiveness has dropped significantly as customers develop defenses against it and economic instability has encouraged lots of people to lower their standards. Eventually, consumer information channels will become just as untrusted as clearly paid advertising is now considered to be, and communication between consumers will be run along the same lines as cold war espionage.

Motivated reasoning

Considering that the hidden assumptions in market efficiency are dependent upon situations even uninformed consumers know from experience are very rare, why would people accept it so easily? The inefficiency of markets has no plausible deniability, but motivated reasoning lowers the bar for plausibility significantly.

During the bulk of the 20th century we could probably argue that anti-communist propaganda played a large role. I don’t think that’s true anymore. Nevertheless, in many circles faith in the invisible hand actually is increasing.

There’s another kind of circular reasoning — one that operates on the currency of guilt and hope. If one accepts market efficiency, it tells the poor that they can rise up through hard work, and it tells the rich that they earned their wealth. This is remarkably similar to the prosperity gospel, which claims that god rewards the righteous with wealth and therefore the poor must have secret sins. It also resembles the mandate of heaven, which claims that all political situations are divinely ordained and therefore disagreeing with the current ruler is sinful.

The similarity between the guilt/hope axis of the market efficiency myth and the prosperity gospel explains the strange marriage between Randian Objectivists and Evangelical Christians found in the religious right. We can reasonably expect many members of this group to be heavily motivated by the desire to believe that the world is fair. It’s not appropriate to characterize this movement as lacking in empathy — empathy is a necessary prerequisite for a guilt so extreme that it makes an elaborate and far-fetched framework for victim-blaming look desirable.

For the poor of this movement, at least on the prosperity gospel side, it might not be so terrible. Motivating a group of people to do the right thing has a good chance of actually improving life generally, even if their promised reward never materialized; second order effects from accidental windfalls are more dangerous, though. (For instance, if you disown your gay son and then win the lottery, you’re liable to get the wrong idea about what “doing the right thing” means).

That said, while the above factors encourage people to trust more strongly in an idea of market efficiency they already accept, bootstrapping the idea of market efficiency is much more difficult.

Natural law, myth vs legend

Market efficiency draws power from an older myth: the idea that money is a natural and universal means of exchange. This is historically and anthropologically dubious. David Graeber, in his book Debt: The First 5,000 Years, makes an argument for the idea that systematic accounting of debts predates the use of actual currency and furthermore only became necessary when cities became large enough to necessitate something resembling modern bureaucracy. Regardless of how accurate that timeline is, we know that gift economies, potlatch, and feasting are more common in tribal nomadic societies than any kind of currency exchange, and that feasting in particular remained extremely important in Europe through the Renaissance.

The legend that backs up the myth of money-as-natural-law takes place in a town. A shoemaker trades shoes for potatoes, but doesn’t want potatoes, so he organizes a neutral currency so that potatoes and apples can be traded for shoes. Graeber points out that this level of specialization couldn’t be ‘natural’ — the town is an appropriate place to set it, since specializing in a particular crop or craft would have been suicidal in the bands of 20–50 people that most humans lived in prior to around 2000 BC.

Our first examples of writing, of course, coincide with the first permanent settlements to have a large enough population to justify heavy specialization. Our first examples of writing are, in fact, spreadsheets recording debt and credit. This, along with the evidence that the unit of currency (the mina of silver) was too substantial for most people to afford even one of (and probably was mostly moved between rooms in the temple complex), is part of Graeber’s argument that independent individuals carrying money for the purpose of direct transactions (i.e., our conception of money) probably only became common later, when imperial armies were expected to feed themselves in foreign lands.

So, on the one hand, it seems to have taken a very long time for the ‘natural’ ‘common sense’ concept of money to take hold among humans. On the other hand, people exposed to the idea of money tend to adapt to it quickly and we have even been able to teach apes to exchange tokens between themselves in exchange for goods and services — in other words, it’s a simple and intuitive system that even animals we mostly don’t consider conscious can grasp.

If something is considered natural law, it’s very easy for people to believe that it is also providence. If something is straightforward and useful in every day life, it’s very easy for people to consider it natural law.

Moral economies

Thoughtful economists tend to recognize the caveats I present here. Some behavioral economists have done great work on illuminating what kinds of things aren’t — or shouldn’t be — subject to the market. This, in turn, illuminates the market myth itself.

It’s possible to think of social relations as economic in nature. Indeed, this is a pretty common model. Transactional psychology presents social interactions as the exchange of a currency of strokes, for instance. Nevertheless, Khaneman presents an experiment that shows social relations aren’t, and shouldn’t, be fungible.

The experiment went like this: a busy day care center has a problem with parents picking up their children late, and instates a fee. Parents in turn respond by picking up their kids late more often, and paying the fee. After the fee is eliminated, the percentage of on-time pickups does not return to the pre-fee state.

Khaneman interprets the results in this way: initially, parents thought of picking their kids up late as incurring a social debt (they were guilty about inconveniencing the day care), the fee reframed it as a service (they can pay some money in exchange for their kids being watched a little longer, guilt-free). But when the fee was eliminated, they felt as though they were getting the service for free.

This result looks a whole lot like the way fines for immoral business practices end up working.

If we consider that, typically, we can make up to people we feel we have wronged, we consider social currency to be somewhat fungible. Nevertheless, exchanging money for social currency is still mostly taboo — paying for sex is widely considered taboo, and even those of us who feel no taboo about sex work would find the idea of someone paying someone else to be their friend a little disturbing. If my Most Unexceptional friend helps me move furniture and I give him a twenty dollar bill, he might be insulted. If I left money on the dresser after having sex with my girlfriend, she might be insulted. (Or consider it a joke.)

We could consider the ease with which money is quantified to be the problem. We rarely can put a number on our guilt or joy. On the other hand, we can generally determine if we feel like we’ve “done enough” to make up for something — our measures of social currency have ordinality, if not cardinality.

Instead, the disconnect is that money is, by design, impersonal. I cannot pay back my guilt over Peter by giving him Paul’s gratitude toward me. This is where transactional psychology’s monetary metaphor for strokes falls apart: a relationship is built up via the exchange of strokes, and that relationship has value based on trust. Meanwhile, any currency has, as a key feature, the ability to operate without trust or even with distrust. Money makes living under paranoia possible, and sometimes even pleasant. But exchange of strokes has its own inherent value, and the trust it builds likewise: it cannot be replaced with money because money’s value is based only on what it can buy.

Speculation

The belief in market efficiency, and the emotional and moral dimensions of that belief, have some unfortunate consequences in speculation. Paradoxically, these consequences are opposed by the myth of money as natural law.

With speculation, one can create money without substance. Promises, bets, and hedges can be nested indefinitely to create value held in superposition. A stake in a speculative market is both credit and debt until it is sold. This is natural, since social constructs are eldrich, operating on fairy logic. This is both a pot of gold and a pile of leaves until I leave the land of the sidhe. Of course, there’s every incentive to oversell, so more often than not it’s a pile of leaves: when too many superpositions collapse, so does the market.

Naive materialism, when it intersects with the idea of money as natural law, finds the eldrich nature of money in speculation disturbing. Isn’t money gold? Or coins? How can something be in my hand and then disappear? So, we get arguments for the gold standard along moral lines: “it’s immoral for something that’s real to behave like fairy dust, so we should limit its growth to match mining efficiency”.

The eldrich behavior of money has some paradoxical results. Being aware that money is a social construct tends to decrease its value (clap your hands if you believe!). The question “if someone burns a million quid on TV, does the value of the pound go up or down” is very had to answer. (If you think you know the answer, substitute a million for a trillion, or for twenty.) On the other hand, being aware of its eldrich nature also tends to slightly decouple one from potentially-destructive drives.

Belief in market efficiency leads successful speculators to believe themselves skilled. While skill at speculation might be possible, statisticians who have studied the problem have generally come to the conclusion that the success distribution is adequately explained by market speculation being entirely random. Unwarranted confidence can lead to larger bets, which (if results are random) means half the time the money disappears into thin air. This does not require malfeasance, misrepresentation, or willful ignorance (as with the 2008 housing crisis). Believing that speculation involves skill is sufficient to cause the market to have larger and larger bubbles and crashes.

*“Western” is neither precise nor correct here. These myths seem to be present in western Europe, North America, Japan, and South Korea. Both China and the former Soviet states have different mythology I’m not qualified to analyse. In the absence of a better term than “western capitalism”, I will use it.

(originally published here: https://modernmythology.net/market-myths-good-bad-and-bazaar-7fa0cbc8f646)

#enkiv2 #essay #capitalism #myth

2 notes · View notes

holytheoristtastemaker · 5 years ago

Link

In this post, we'll see what atomic CSS is, how it relates to functional / utility-first CSS like TailwindCSS, and that big players are adopting it in their modern React codebases. As I'm not a expert of this subject, don't expect a deep dive about the pros and cons. I just hope you get an idea about what it's about. Note: Atomic CSS is not really related to Atomic Design.

What is atomic CSS?

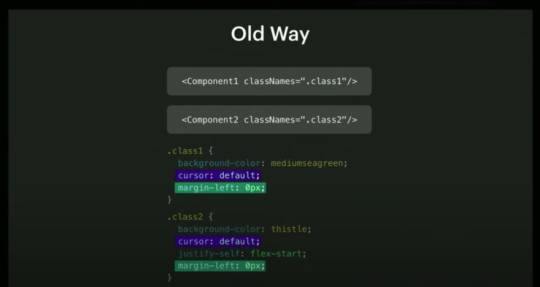
You may have heard of various CSS methodologies like BEM, OOCSS...

<button class="button button--state-danger"> Danger button </button>

These days, people really like Tailwind CSS and its utility-first concept. This is close to Functional CSS and Tachyon.

<button class="bg-blue-500 hover:bg-blue-700 text-white font-bold py-2 px-4 rounded"> Button </button>

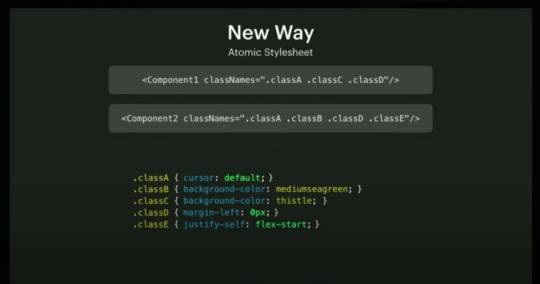
With a stylesheet of a bunch of utility classes, you can go a long way. Atomic CSS is like an extreme version of utility-first CSS: all CSS classes have a single, unique CSS rule. Atomic CSS was first used by Thierry Koblentz (Yahoo!), in Challenging CSS Best Practices in 2013.

/* Atomic CSS */ .bw-2x { border-width: 2px; } .bss { border-style: solid; } .sans { font-style: sans-serif; } .p-1x { padding: 10px; } /* Not atomic, because the class contains 2 rules */ .p-1x-sans { padding: 10px; font-style: sans-serif; }

With utility/atomic CSS, we acknowledge it's ok to couple the structure and presentation layers: when we need to change the button color, we modify the HTML, not the CSS. This tight coupling is also acknowledged in modern CSS-in-JS React codebases, but it seems the CSS world figured out first that the "separation of concern" of the web didn't feel right. Specificity is also less a problem, as we use simple class selectors. We are now styling via the markup, which has several interesting properties:

the stylesheet grows less as we add new features

we can move the markup around, and the styles are moved at the same time

we can remove features, and be sure that we remove the related styling at the same time

For sure, the html is a bit more bloated. This can be a concern for server rendered web apps, but the high redundancy in class names compress well with gzip, in the same way it worked well for duplicated css rules previously found in your CSS files. You don't need to use utility/atomic CSS for every cases, just the most common styling patterns. Once your utility/atomic CSS is ready, it will not change or grow much. It's possible to cache it more aggressively (you can append it to vendor.css for example, and expect it to not invalidate across app redeploys). It is also quite portable, and you can use it in other applications.

Limits of utility/atomic CSS

Utility/atomic CSS looks interesting, but they come with a few challenges as well. People usually write utility/atomic CSS by hand, carefully crafting naming conventions. It can be hard to ensure the convention is easy to use, consistent, and not bloated over time. Can multiple persons work on this CSS and keep it consistent? Is it subject to the bus factor? You also need to work on a good utility/atomic stylesheet up-front, before being able to iterate on features that will use it. If the utility/atomic CSS is made by someone else, you will have to learn the class naming conventions first (even if you know everything about CSS). This convention is opiniated, and it's possible that you don't like it. Sometimes, you need some extra CSS that is not provided by your utility/atomic CSS. There's no unique way to provide the remaining one-off styles.

Tailwind to the rescue

The approach of Tailwind is very convenient, and solves some of these problems. It does not really provide a unique utility CSS file for all websites. Instead, it only provides a shared scope and naming conventions. From a configuration file, it allows you to generate your own custom utility CSS. Knowledge of Tailwind is portable to other applications, even if they don't use exactly the same class names. It reminds me a bit of the "Learn once, write anywhere" philosophy of React. I've seen people reporting that Tailwind classes cover something between 90% or 95% of their needs. It seems the scope is large enough, and we don't often need to use one-off style. At this point you might wonder why use atomic CSS instead of Tailwind?. What would you gain in enforcing the atomic CSS rule of 1 rule, 1 class? You would end up with a larger html markup, and a less convenient naming convention? Tailwind already has many atomic classes anyway. So, should we abandon the idea of atomic CSS, and simply use Tailwind? Tailwind is a great solution, but there are still a few problems that remain unsolved:

the need to learn an opiniated naming convention

CSS rules insertion order still matters

can unused rules be easily removed?

what do we do with the remaining one-off styles?

Handwritten atomic CSS might not be the most convenient compared to Tailwind.

Comparison with CSS-in-JS

There's a relationship with CSS-in-JS, and utility/atomic CSS. Both approaches advocate for styling from the markup, somehow trying to emulate performant inline styles, which gives them many similar properties (like the ability to move things around with confidence). Christopher Chedeau greatly helped spread the idea of CSS-in-JS in the React ecosystem. In multiple talks, he explains the problems of CSS:

Utility/atomic CSS solve some of these problems too, but definitively not all (particularly, the non-deterministic resolution of styles). If they share similarities, can't we use them both together?

Enter atomic CSS-in-JS

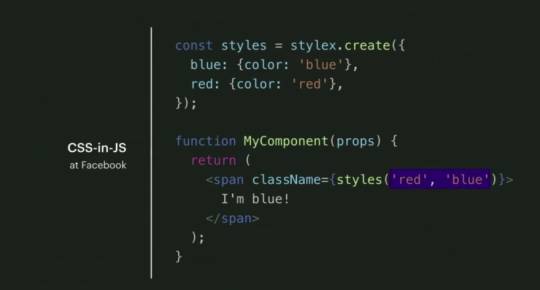
Atomic CSS-in-JS can be seen as "automatic atomic CSS":

You don't need to create a class name convention anymore

Common and one-off styles are treated the same way

Ability extract the critical CSS of a page, and do code-splitting

An opportunity to fix the CSS rules insertion order issues in JS

I'm not aware about all CSS-in-JS libraries out there currently supporting atomic CSS. Supporting it is actually an implementation detail of the CSS-in-JS library. Support might come and go, or can even be made optional. I will highlight 2 particular solutions, that recently lead to 2 large-scale atomic CSS-in-JS deployments, using 2 talks as sources:

React-Native-Web at Twitter (more details in Nicolas Gallagher's talk)

Stylex at Facebook (more details in Frank Yan's talk)

See also: Styletron, Fela, cxs

React-Native-Web

React-Native-Web is a very interesting library: it permits to render React-Native primitives on the web. We are not really talking about cross-platform mobile/web development here (watch the talks for more details). As a web developer, you just need to understand that React-Native-Web is a regular CSS-in-JS library, that comes with a small set of primitive React components. Wherever you see View, you can replace it in your mind with div, and you are good to go. React-Native-Web has been created by Nicolas Gallagher, working on Twitter mobile. They progressively deployed it to mobile, not sure when exactly but probably around 2017/2018. Since then, it has been used by other companies (Major League Soccer, Flipkart, Uber, The Times...), but the most significant deployment has been the new 2019 Twitter desktop app by a team lead by Paul Armstrong.

Stylex

Stylex is a new CSS-in-JS library developed at Facebook for the 2020 Facebook rewrite (currently in beta). It seems they plan to open-source it some day, possibly under a different name. It's worth mentioning that Nicolas Gallagher, the author of React-Native-Web, was hired by Facebook 2 years ago. It's not a big surprise to see some of its concept being reused by Facebook. Unlike React-Native-Web, Stylex does not seem focused on cross-platform development. All the infos I have are from the talk :) We'll have to wait for more details.

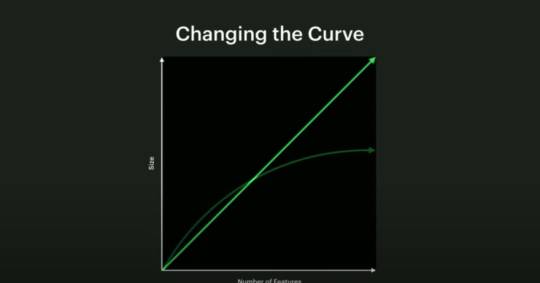
Scalability

As expected with atomic CSS, both Twitter and Facebook have seen a massive reduction of their CSS, as it now follows a logarithmic curve. There's an initial price to pay for simple apps though.

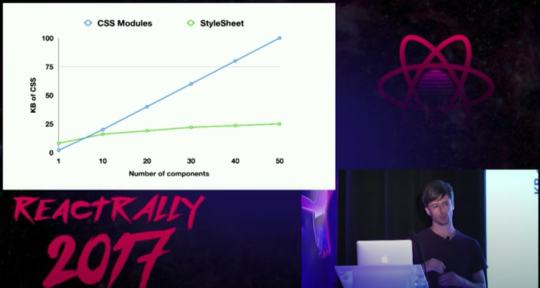
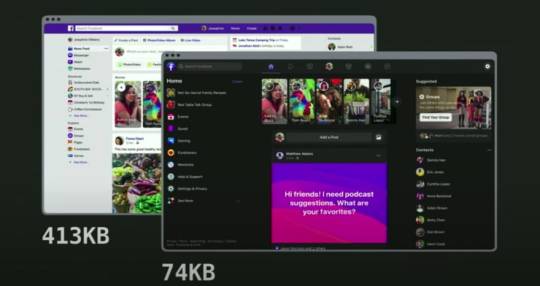
Facebook shared concrete numbers:

Their old site was 413Kb of CSS just for the landing page

Their new site is 74Kb for the whole site, including the dark mode

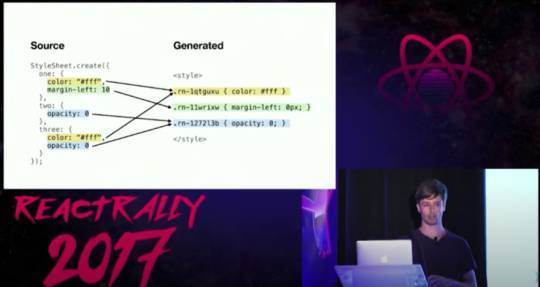
Source and output

The 2 libraries looks quite similar here, but it's hard to say, considering we don't know much about Stylex. It's worth highlighting React-Native-Web will expand the CSS shortand syntaxes like margin: 0.

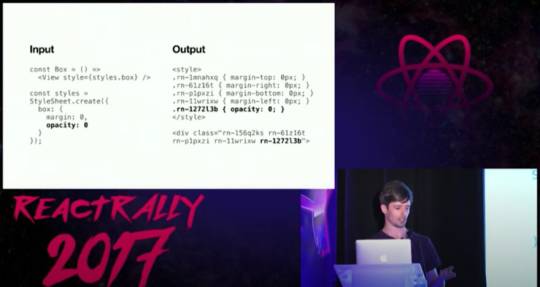
Production inspection

Let's look at what the markup looks like on Twitter:

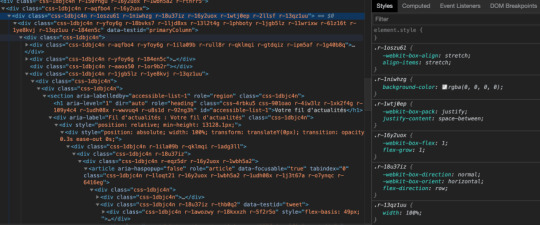
Now, let's look at the new Facebook:

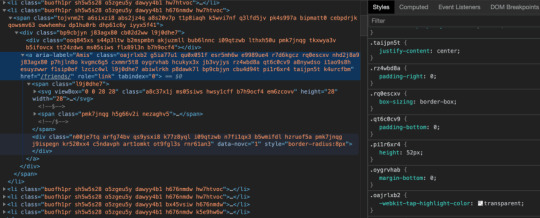
Many people will probably be horrified when seeing this, but it actually works, and remains accessible. It might be a bit harder to navigate styles in the Chrome inspector, but devtools can help:

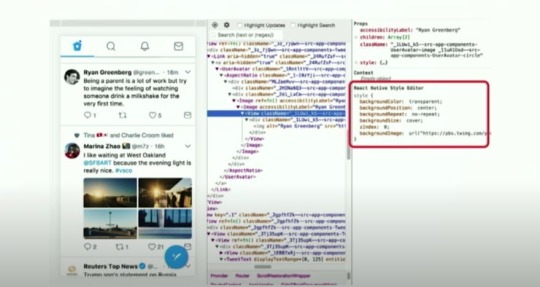
CSS rules order

Unlike handwritten utility/atomic CSS, the JS libs are able to make the styling not dependent of the CSS rules insertion order. As you may know, in case of conflicting rules, it's not the last class of a class attribute that wins, but the rule that is inserted last in the stylesheet. Specificity issues are solved by only using simple class-based selectors.

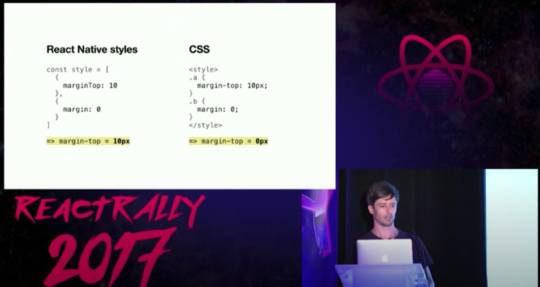
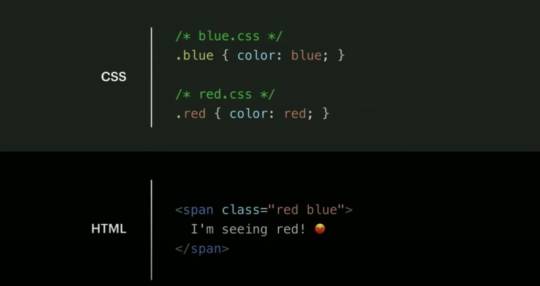
In practice, these libraries avoid outputting classes with conflicting rules on the same element. They ensure that the last style declared in the markup always wins. The "overridden classes" are filtered, and don't even make it to the DOM.

const styles = pseudoLib.create({ red: {color: "red"}, blue: {color: "blue"}, }); // That div only will have a single atomic class (not 2!), for the blue color <div style={[styles.red, styles.blue]}> Always blue! </div> // That div only will have a single atomic class (not 2!), for the red color <div style={[styles.blue, styles.red]}> Always red! </div>

Note: This predictable behavior is only possible thanks to using the most strict atomic CSS. If a class had multiple rules, and only one of them was overridden, the CSS-in-JS library wouldn't be able to filter that class without removing the non-overridden rules as well. If a class had a single shorthand rule like margin: 0, and the override was marginTop: 10, it's the same problem. The shorthand syntax like margin: 0 is expanded to 4 distinct classes, and the library is able to filter overridden classes that should not appear in the DOM with more granularity.

You still prefer Tailwind?

Once you know all the Tailwind naming conventions, you can code an UI very fast. It might feel less productive to go back to writing every CSS rule by hand, like you do in CSS-in-JS. Nothing prevents your for building your own abstractions on top of an atomic CSS-in-JS framework. Styled-system might be able to run some of the CSS-in-JS libraries supporting atomic CSS. It's even possible to reuse naming conventions for Tailwind in JS, if you feel you are productive with it. Let's take some Tailwind code:

Now, let's take a random solution (react-native-web-tailwindcss) I just found on google:

import {t} from 'react-native-tailwindcss'; <View style={[t.absolute, t.inset0, t.p4, t.bgBlue500]} />

In term of productivity, this is not very different. And you could avoid typos with TypeScript.

Conclusion

To me, using Atomic CSS, CSS-in-JS, and Tailwind all at the same time makes sense. That's almost everything I have to say about atomic CSS-in-JS. I have never used atomic CSS, atomic CSS-in-JS, or Tailwind in any large production deployment. I'm probably wrong on some parts, feel free to correct me on Twitter. I think atomic CSS-in-JS is a trend to watch in the React ecosystem, and I hope you learned something useful with this post. As I've not been able to find any article about atomic CSS-in-JS, I wrote this mostly for myself. I want a resource to link to when I mention atomic CSS-in-JS in upcoming blog posts (I plan to write more articles about React-Native-Web and cross-platform, stay tuned). Thank you for reading.

0 notes

acdemic · 8 years ago

Photo

hey hello hi!!! it’s been ages (6 months?!) since my last masterpost, and i’ve been seeing so many great educational apps on the google play store. so here’s a list of some educational smartphone apps that you should check out!

disclaimer: i have not used most of these applications (i generally don’t use study or even productivity apps), so i’m recommending them based on reviews!

general education

curiosity [ play store, free ] [ apple, free ] curiosity is a super cool app that’s all about learning new quirky facts! every 24 hours new content is released, including mind-blowing science, history and technology facts. it’s like having the best museum and the most fascinating library at your disposal.

coursera [ play store, free ] [ apple, free ] with coursera, you can access more than 1,000 courses and specializations developed by 140+ of the best colleges and universities in the world, and master subjects from python programming and data science to photography and music.

edx [ play store, free ] [ apple, free ] edx provides free online courses from the world’s best universities and institutions. there are so many topics to discover, including computer science, engineering, history, psychology, nutrition, big data, statistics and hundreds more. with edx, you have the flexibility to learn on your schedule. it is free education, when and where you want it.

khan academy [ play store, free ] [ apple, free ] khan academy allows you to learn (almost) anything for free. browse over 10,000 videos and explanations at your fingertips in math, science, economics, history, and much, much more. sharpen your skills with over 40,000 interactive practice questions with instant feedback and step-by-step hints. khan academy is a wealth of resources and it’s all free! note: i really really recommend khan academy! it is super helpful and there’s also the free sat prep (and the upcoming free lsat prep for people interested in law school)!!

udemy [ play store, free ] [ apple, free ] udemy is your place to learn real world skills online. with over 32,000 online courses and tutorials, offered in more than 80 languages, you can choose from a wide range of topics to inspire creativity, hone your skills, be your own boss, and more. courses in everything from programming, it & software, business, marketing and entrepreneurship, health, design, languages, music, and much more.

goodwall [ play store, free ] [ apple, free ] goodwall is basically a social network for students - you can share your skills and achievements and win scholarships (and even be recognized by colleges and universities!) when you join, you are eligible for a $500 weekly new student award, in addition to the $1000 student of the month scholarship. people seem to think that it’s a great way to connect to other motivated students throughout the world (obviously the studyblr community is The Best ;) but here’s an awesome alternative!)

schoold [ play store, free ] [ apple, free ] schoold is a super cool app that allows you to find information on 3000+ colleges and 25k+ scholarships by major and admission chance. It also offers free college counseling (advice on applications, financial aid, majors, and careers) and future planning tools!

science

phywiz [ play store, free ] need help with your physics homework? phywiz provides step by step solutions for questions in over 30 physics topics, including kinematics, forces, gravity, and quantum physics. ask phywiz a question like "if mass is 6 and velocity is 7, what is momentum?" and get your answer immediately. many of the positive reviews call it “one of the best apps i’ve ever used”.

little alchemy [ play store, free ] [ apple, free ] [ website ] this is such a cute game where you start with four elements and combine them to create interesting, fun and surprising items. it’s definitely addictive!

chemistry quiz [ play store, free ] 500+ quiz questions covering the elements, the periodic table, bonding and interactions, matter and mixtures, chemical reactions, acids and bases, organic chemistry, nuclear chemistry, history of chemistry, and labs.

skyview [ play store, free ] [ apple, free ] a beautiful and intuitive stargazing app that uses your camera to precisely spot and identify celestial objects in sky, day or night. it’s a great app for people who love space but don’t want to purchase fancy equipment to enjoy its beauty. you can see what each star and planet is and where it’s going. be sure to calibrate it first!

coding

encode [ play store, free ] encode is packed with bite-sized coding lessons that combine succinct explanations and clear real-code examples. it is a wonderful way for beginners to start programming.

sololearn has a ton of apps that are all about learning to code: java, c#, python, javascript, c++, etc.!

programming hub [ play store, free ] [ apple, free ] your one-stop solution to learn all of the top programming languages! you can learn c, c++, java, html, javascript, r, css, vb.net, c#, python 2.7, python 3, linux shell scripting, swift, sql, jquery, and assembly 8086. there are over 1800+ pre-compiled programs with output for practice and learning. a new feature seems to be the programming-related interview questions that can help you prepare for a job interview!

codenza [ play store, free ] codenza is a dictionary of 3000+ ready-made computer programs: the ultimate coding encyclopedia for university curriculum. codenza covers everything from computer graphs to artificial intelligence! note: codenza does not teach programming. it only provides programs and offers explanations for the more complex programs.

math

cymath [ play store, free ] [ apple, free ] [ website ] stuck on a math problem? cymath allows you to enter your problem, and helps you to solve it step-by-step. topics include pre-algebra, algebra (equation solving, factoring, logarithms, exponents, complex numbers, quadratic equations, trigonometry, partial fraction, polynomial division, etc.), and calculus (product rule, quotient rule, chain rule, u-substitution, integration by parts, integration by partial fraction, trigonometric substitution, rationalizing substitution, etc.)

photomath [ play store, free ] [ apple, free ] math is full of symbols that we are inconvenient to type, and photomath solves that problem: simply point your camera toward a math problem and photomath will show the result with detailed step-by-step instructions. there is a new feature of handwriting recognition as well!

mathway [ play store, free ] [ apple, free ] [ website ] yet another math problem solver! this one allows you to type your problem or scan a picture of your problem. mathway covers basic math, pre-algebra, algebra, trigonometry, precalculus, calculus, statistics, finite math, linear algebra, chemistry, and graphing. one flaw seems to be that you need to be online for it to work, but otherwise, it’s a fantastic tool!

history

history timeline [ play store, free ] okay, woah. this is a detailed timeline of world history with thousands of entries! it includes world history (events, nations, leaders, and wars) AND history of science, art, literature, music, and philosophy.

today in history [ play store, free ] [ similar apple, free ] for the history enthusiast who wants to learn something new every day: today in history tells you what historical events happened on that day! it works offline and you can choose from over 50 languages.

ancient history encyclopedia [ play store, free ] [ website ] thousands of informative and reliable articles on ancient history. articles are written with students in mind and are carefully reviewed to ensure accuracy, and are easy to read.

languages

duolingo [ play store, free ] [ apple, free ] one of the leading language learning apps, duolingo gives you the ability to learn english, spanish, french, german, italian, portuguese, dutch, irish, danish, swedish, russian, ukrainian, esperanto, polish, and turkish for free. you can practice your speaking, reading, listening, and writing skills and improve your vocabulary and grammar.

productivity

forest [ play store, free ] [ apple, $1.99 ] forest is a cute productivity app that keeps you off of your phone! you set a certain amount of time, and during that time a tree ‘grows’, but if you use your phone before the times up, the tree dies. :(

habitica [ play store, free ] [ apple, free ] have you heard of ‘gamification’? habitica is an app that allows you to gamify your tasks! check off tasks to level up your avatar and unlock features such as armor, pets, skills, and even quests! it’s a great way to have fun while being productive! note: habitica is another one of these apps that i’ve actually attempted to use - it is super cute and it’s definitely a great way to stay on track!

timetune [ play store, free ] timetune is a great app for people who have established a daily routine or would like to. you can set up a routine (or multiple routines) and add your daily tasks. it can be used as a daily task reminder, student calendar, timetable planner, routine schedule organizer, routine optimizer, habit creation tool, daily time manager, or daily planner.

ike [ play store, free ] ike is a to-do list that uses eisenhower’s priority matrix. you can organize your tasks by importance and urgency, and add all sorts of details such as due dates and location reminders.

habithub [ play store, free ] habithub is based on seinfeld’s productivity secret, which involves building long streaks of days that will motivate you to keep moving forward. (snapchat for habits? i think yes!) it includes a full calendar view for every habit, reminders, compatibility with smartwatches, the option to write notes every day, more flexible goals, the ability to categorize your habits, and graphs that show you how you’re doing. the interface looks beautiful and people seem to love the abundance of settings.

pomotodo [ play store, free ] [ apple, free ] there is an abundance of pomodoro timers in the app store, and pomotodo is one of them! pomotodo easily syncs across platforms, has advanced to-do list options, the ability to customize pomo and break times, offers background noise to keep you focused, and sends you weekly email reports to help you track your productivity. i don’t want to list a ton pomodoro apps in this masterpost, but here are the many options on google play store!

alright, that’s all i’ve got for you today !! i hope that this was helpful, and feel free to send me an ask with any questions, suggestions for future masterposts, or your recommendations for other study apps/websites!! :) have a great day!

icon by madebyoliver

8K notes · View notes

lettersfromtaiwan · 8 years ago

Text

Same-Sex Marriage In Taiwan: Progression Via Judicial Review In Spite Of A Passive Centrist Politics

On the 24th May, Taiwan’s Council of Grand Justices issued Constitutional Interpretation No. 748 in which they stated that The Civil Code violates the freedom of marriage and equal rights for all citizens as guaranteed by the Constitution, and that If the government has not changed the law in two years, same-sex couples will be allowed to register their union at household registration offices. This has since proven to be a destructive mistake. Marriages across the nation are falling apart as heterosexual couples realise that their union is not only no longer sacrosanct but has also been stripped of any meaning. Young impressionable students across Facebook and LINE are declaring their desire to marry themselves and their pets, and at least one of the remaining statutes of Chiang Kai-shek has been spotted weeping. Traditional Chinese culture and Confucian values are dead. The malaise of Western liberalism has destroyed yet another nation. That at least, with little exaggeration, was the prognosis of what would happen should same-sex marriage be legalised. What has actually happened is that the nation has spent a day or two in mild celebration that the Council of Grand Justices affirmed that some of the rights laid out in the Constitution do actually apply to everyone, as is the purpose of a Constitution. There has been little of a social, or political earthquake in response to the ruling, but for those who campaigned so hard to enjoy a basic right to join in a legally recognised union with the person they love regardless of their sex or gender, it was a seismic moment. It is one that Taiwan should rightly be proud of as the first country in Asia to release the institution of marriage from illogical and exclusionary heteronormative constraint.

The ruling is also interesting for the response to it. The new Chairman of the KMT, Wu Den-yih (吳敦義), and also party grandee Jason Hu (胡志強), quickly came out with statements in support of the ruling, much to the surprise of netizens who were also quick to point out that the Chairman had previously publicly stated his opposition to it. That a politician would flip their position after measuring which direction the vane of public opinion had swung is both opportunistic but also in some respects welcome. It shows at least that they are capable of change. Their previously strong and consistent opposition to same-sex marriage will not however be forgotten by those who suffered in the period of struggle to gain those rights, and their quick change of heart and the mendacious and revisionist claim to have always supported same-sex marriage will not earn the public’s trust. You don’t get a gold star for lacking moral certitude and courage in battle until someone else has won the war and its time to line up for a medal. Most interestingly though, despite all the protests from US-funded and inspired evangelicals before the ruling, the vast majority of Taiwanese seem perfectly at ease with the ruling and its implications, or at least do not feel threatened by them. The main reason for this collective shrug is probably because the ruling doesn’t actually affect anyone negatively - it only expands a right enjoyed by the vast majority. It turns out that expanding this right to marriage was not a zero-sum equation and did not devalue, denigrate, or render less sacrosanct, marriages between heterosexual couples. As much as ‘love trumped hate’, logic triumphed over a tendency to visceral reaction.

What the response also highlighted was that ‘public opinion’ has at least two dimensions in Taiwan, and I suspect in other developed liberal democratic nations: a private held or intimately shared liberalism, with a small ‘l’, and a publicly expressed and socially nervous reactionary and performative conservatism. As a business which generates more consumption of its product when events are more polarising and sensational, the media seek out the latter over the former, thereby distorting the image people have of what most of their fellow citizens think. A desire to fit in and swim with the tide is a powerful component of culture in Taiwan, as it is elsewhere in countries around the world. The death penalty is a good example in this respect. Both KMT and DPP administrations shy away from addressing the failure of capital punishment to act as a deterrent, the former wielding it as a means to project strength and as tool for political distraction, the latter cautious of handling a political hot potato which it feels does not have sufficient public consensus to take the electoral risk of addressing. One wonders how many wrongful executions will be tolerated before public consensus is deemed sufficient for politicians to find the courage to bring Taiwan in line with the vast majority of other nations and abolish this cruel and ineffective practice.

Significantly, it should be noted that the same-sex ruling was not only a top down effort but a citizen-led one: Chi Chia-wei (祁家威) filed a request for an interpretation in 2015 after his attempt to register his same-sex marriage was rejected by Taipei’s Wanhua District (萬華) household registration office in 2013 and subsequent court appeals failed. The other request was filed by the Taipei Department of Civil Affairs in 2015. The Legislative Yuan, even with a clear and historic DPP majority had stumbled over amending the civil code and / or introducing new law. The President had made clear her support for same-sex marriage but her party’s caucus had failed to evince unity or creativity over the issue. National level politicians had sat on the fence and essentially waited for the judiciary to settle the case for them. Sadly, it is very doubtful such an approach would work with the death penalty in Taiwan this year and perhaps still for years to come. Where allowing everyone to marry does not install fear or loathing in the populace, it seems not executing murderers is still a logical step too far for many, if opinion polls are to believed.

The mark of a progressive and liberal democracy is how society’s outliers and its most vulnerable are treated. A party or government which claims to be truly progressive will not just reflect public opinion but have the political courage, especially when in power, to lead positive change, even when seemingly unpopular, which reflects the nation’s humanity and protects everyone, not just those the public is willing to express sympathy for. It should be a determined force for institutionalising empathy over sympathy, tolerance over spite, inclusion over ring-fencing, and safeguards over abandonment. ‘Progress’ in society as a whole is not a measure of economic and technological development but one where gross domestic happiness, trust, and security are maximised.

Politics and economics are not separate. Nodding to the left to superficially ameliorate the continent negative impacts of maintaining a dominant right-wing model of political economy is both morally bankrupt, exploitative, and ultimately only creates political space and legitimacy for more extreme voices on the right. The popularity of (domestically liberal yet internationally reactionary) Bernie Sanders in the US, and the electoral success of genuine progressive Left Jeremy Corbyn in the UK on June 8th, shows that the current forty year hegemony of neoliberalism has lost public trust. The election of Donald Trump as President is evidence that the empty logarithm-driven sloganism of “I’m With Her”, and the neoliberal incrementalist agenda it papers over, offers no vision or hope or answer to any number of collective problems such as climate change, an end to the war on drugs and terror economies, or how to address building the fiscally sustainable national, universal healthcare system that all tax-payers and citizens should deserve as a basic human right. “En-Marche” in 2017 is no safeguard against a President Le Pen in 2022. If anything it will be an invitation for it, especially once the electorate cottons onto his Obamaesque style of camouflaging centre-right economics with sound-bites and PR stunts that appropriate the left for clickatvist popularity spikes. The performative liberalism of Trudeau will not for long mask his deeply illiberal security and energy policies, or the willingness of his administration to bend at the knee in the face of pressure from Beijing.

President Tsai would do well to look abroad and take note that Trump is a supernova whose logical end is implosion and a political black hole that could easily suck the US into a vicious and destructive spiral of domestic institutional and social conflict which could even result in open and bloody insurrection. Politics across the world are becoming more extreme and polarised as people start realising that continuing as normal is collective suicide by inequality and climate. If Tsai wants to lead a truly progressive DPP, she should not be afraid to lead with courage and conviction, to make the case that there are other more humane, and affordable, models of political economy which better ensure basic human rights, such as marriage and a clean environment, sooner and for generations to come.

#marriageequality #LGBTQIA #same-sex marriage #Taiwan #Asia

6 notes · View notes

toppersexam · 5 years ago

Text

NDA 2020 Age Limit, Syllabus, Online Free Mock Test, MCQ, Books

NDA 2020 Age Limit, Syllabus, Online Free Mock Test, MCQ, Books NDA (II) 2020 Rejected applicants list has been published due to non-payment of exam fee. Admit Card is releasing soon. The exam will be conducted by Union Public Service Commission (UPSC). UPSC NDA entrance exam is a gateway for the aspirants who want to make their career in Indian Army, Navy and Air Force. NDA Age Limit It should be clearly noted that only unmarried male candidates, who are not born earlier than July 2, 2001 and not later than July 1, 2004 are eligible to appear for NDA 1 Exam. For NDA 2 2020, candidates must be born between January 2, 2002 and January 1, 2005.

NDA Free Online Mock Test Crack NDA Recruitment exam with the help of online mock test Series or Free Mock Test. Every Sample Paper in NDA Exam has a designated weightage so do not miss out any Paper. Prepare and Practice Mock for NDA exam and check your test scores. You can get an experience by doing the Free Online Test or Sample Paper of NDA Exam. Free Mock Test will help you to analysis your performance in the Examination. NDA Free Online Mock Test : Available Now NDA MCQs Buy the question bank or online quiz of NDA Exam Going through the NDA Exam Question Bank is a must for aspirants to both understand the exam structure as well as be well prepared to attempt the exam. The first step towards both preparation as well as revision is to practice from NDA Exam with the help of Question Bank or Online quiz. We will provide you the questions with detailed answer. NDA MCQs : Available Now NDA 2020 Syllabus Paper-1 : Mathematics Algebra 1. relation, Logarithms and their applications. 2. equivalence relation. 3. Representation of real numbers on a line. 4. Complex numbers—basic properties, 5. modulus, argument, Binomial theorem and its applications 6. cube roots of unity. 7. Solution of linear inequations of two variables by graphs. 8. Binary system of numbers. 9. Conversion of a number in decimal system to binary system and vice-versa. 10. Arithmetic, Permutation and Combination. 11. Geometric and Harmonic progressions. 12. Quadratic equations with real coefficients. 13. Solution of linear inequations of two variables by graphs. Matrices and Determinants 1. Types of matrices, Adjoint and inverse of a square matrix, 2. operations on matrices.basic properties of determinants. 3. Determinant of a matrix, 4. Applications-Solution of a system of linear equations in two or three unknowns by Cramer’s rule and by Matrix Method. Trigonometry 1. Angles and their measures in degrees and in radians. 2. Trigonometrical ratios. 3. Trigonometric identities Sum and difference formulae. 4. Multiple and Sub-multiple angles. 5. Inverse trigonometric functions. 6. Applications-Height and distance, 7. properties of triangles. Analytical Geometry of Two and Three Dimensions 1. Rectangular Cartesian Coordinate system. 2. Distance formula.Direction Cosines and direction ratios. 3. Equation of a line in various forms. 4. Angle between two lines. 5. Distance of a point from a line. 6. Equation of a circle in standard and in general form. 7. Standard forms of parabola,Equation of a sphere. 8. ellipse and hyperbola.Equation two points. 9. Eccentricity and axis of a conic. 10. Point in a three dimensional space, 11. distance between two points. 12. Direction Cosines and direction ratios. 15. Equation of a plane and a line in various forms. 16. Angle between two lines and angle between two planes. Differential Calculus 1. Concept of a real valued function–domain, 2. range and graph of a function. 3. Composite functions, Derivatives of sum, 4. one to one, Increasing and decreasing functions. 5. onto and inverse functions. 6. Notion of limit, Second order derivatives. 7. Standard limits—examples. 8. Continuity of functions - examples, 9. algebraic operations on continuous functions. 10. Derivative of function at a point, 11. geometrical and physical interpretation of a derivative-application. 12. derivative of a function with respect to another function, 13. product and quotient of functions, 15. derivative of a composite function. 16. Application of derivatives in problems of maxima and minima Integral Calculus and Differential Equations 1. Integration as inverse of differentiation, 2. integration by substitution and by parts, 3. standard integrals involving algebraic expressions, 4. trigonometric, Application in problems of growth and decay. 5. exponential and hyperbolic functions. 6. Evaluation of definite integrals—determination of areas of plane regions bounded by curves—applications. 7. Definition of order and degree of a differential equation, 8. formation of a differential equation by examples. 9. General and particular solution of a differential equations, 10. solution of first order and first degree differential equations of various types—examples. Victor Algebra 1. Vectors in two and three dimensions, 2. magnitude and direction of a vector. 3. Unit and null vectors, addition of vectors, 4. Applications—work done by a force and moment of a force and in geometrical problems. 5. scalar multiplication of a vector, 6. scalar product or dot product of two vectors. 7. Vector product or cross product of two vectors. Statistics and Probability 1. Statistics: Classification of data, 2. Frequency distribution, Conditional probability, 3. cumulative frequency distribution - examples. 4. Graphical representation - Histogram, 5. Pie Chart, frequency polygon—examples. Measures of Central tendency— Mean, median and mode. 6. Variance and standard deviation determination and comparison. 7. Correlation and regression.Probability: Random experiment, 8. outcomes and associated sample space, events, 9. mutually exclusive and exhaustive events, impossible and certain events. 10. Union and Intersection of events. Complementary, 11. elementary and composite events. Definition of probability—classical and statistical—examples. 12 .Elementary theorems on probability—simple problems. 13 .Bayes’ theorem—simple problems. Random variable as function on a sample space. 14 .Binomial distribution, 15. examples of random experiments giving rise to Binominal distribution. Paper-2 : General Ability Test English 1. Grammar and usage, vocabulary, comprehension General Knowledge Physics 1. Physical Properties and States of Matter, 2. Mass, Weight, Volume, 3. Density and Specific Gravity, Principle of Archimedes, 4. Pressure Barometer. Motion of objects, 5. Velocity and Acceleration, Newton’s Laws of Motion, 6. Force and Momentum, Parallelogram of Forces, 7. Stability and Equilibrium of bodies, Gravitation, 8. elementary ideas of work, Power and Energy. 9. Effects of Heat, Measurement of Temperature and Heat, 10. change of State and Latent Heat, Modes of transference of Heat. 11. Sound waves and their properties, Simple musical instruments. 12. Rectilinear propagation of Light, Reflection and refraction. 13. Spherical mirrors and Lenses, Human Eye. 14. Natural and Artificial Magnets, Properties of a Magnet, 15. Earth as a Magnet.Static and Current Electricity, 16. conductors and Non-conductors,Ohm’s Law, 17. Simple Electrical Circuits, Heating, 18. Lighting and Magnetic effects of Current, 19. Measurement of Electrical Power, 20. Primary and Secondary Cells, Use of X-Rays. 21. General Principles in the working of the following: 22. Simple Pendulum, Simple Pulleys, Siphon, 23. Levers, Balloon,Pumps, Hydrometer, 24. Pressure Cooker, Thermos Flask, Gramophone, 25. Telegraphs, Telephone, Periscope, Telescope, 26. Microscope, Mariner’s Compass; 27. Lightening Conductors, Safety Fuses Chemistry 1. Physical and Chemical changes. 2. Elements, Carbon - different forms. 3. Mixtures and Compounds, 4. Symbols, Fertilizers—Natural and Artificial. 5. Formulae and simple Chemical Equations, 6. Law of Chemical Combination (excluding problems). 7. Properties of Air and Water. 8. Preparation and Properties of Hydrogen, 9. Oxygen,Glass, Ink, Paper, Cement, 10. Nitrogen and Carbondioxide, 11. Oxidation and Reduction. 12. Acids, bases and salts. 13. Material used in the preparation of substances like Soap, 14. Paints, Safety Matches and Gun-Powder. 15. Elementary ideas about the structure of Atom, Atomic Equivalent and Molecular Weights, Valency. General Science 1. Difference between the living and non-living. Basis of Life—Cells, 2. Protoplasms and Tissues. Growth and Reproduction in Plants and Animals. 3. Elementary knowledge of Human Body and its important organs. 4. Common Epidemics, their causes and prevention. 5. Food—Source of Energy for man. Constituents of food, 6. Balanced Diet. The Solar System—Meteors and Comets, 7. Eclipses. Achievements of Eminent Scientists. History Freedom Movement 1. A broad survey of Indian History, with emphasis on Culture and Civilisation. 2. Freedom Movement in India. Elementary study of Indian Constitution and Administration. 3. Elementary knowledge of Five Year Plans of India. 4. Panchayati Raj, Co-operatives and Community Development. 5. Bhoodan, Sarvodaya, National Integration and Welfare State, 6. Basic Teachings of Mahatma Gandhi.Exploration and Discovery; 7. Forces shaping the modern world; Renaissance, 8. War of American Independence. French Revolution, 9. Industrial Revolution and Russian Revolution. 10. Impact of Science and Technology on Society. 11. Concept of one World, United Nations, Panchsheel, 12. Democracy, Socialism and Communism. Role of India in the present world. Geography 1. The Earth, its shape and size. Lattitudes and Longitudes, 2. Concept of time. International Date Line. . 3. Origin of Earth. Rocks and their classification; 4. Weathering-Mechanical and Chemical, 5. Earthquakes and Volcanoes.Movements of Earth and their effects. 6. Ocean Currents and Tides Atmosphere and its composition; 7. Temperature and Atmospheric Pressure, 8. Planetary Winds, Cyclones and Anti-cyclones; 9. Humidity; Condensation and Precipitation; 10. Types of Climate, Major Natural regions of the World. 11. Regional Geography of India—Climate, Natural vegetation. 12. Mineral and Power resources; 13. location and distribution of agricultural and Industrial activities. 14. Important Sea ports and main sea, 15. land and air routes of India. Main items of Imports and Exports of India. Current Events 1. Knowledge of Important events that have happened in India in the recent years. 2. Current important world events. 3. Prominent personalities—both Indian and International including those connected with cultural activities and sports. NDA Exam Pattern 2020 Negative Marking : Mathematics : 0.83 General Abilities : 1.33 PaperSubjectNo. of QuestionMarksDuration Paper -1 Mathematics120300150 Minutes Paper - IIGeneral Ability Test (English & General Knowledge)

#NDA NDA2020 NDAExam FreeTestSeries QuestionsBank NDASyllabus OnlineTestSeries OnlineMockTest ImportantQuestionPaper ImportantQuestion Import

0 notes

pathfinderdefenceacademyposts · 5 years ago

Text

Best NDA Coaching Classes in Lucknow | Best NDA Coaching Center in Lucknow

Pathfinder Defence Academy is one of the Best NDA Coaching in Lucknow. Best Defence Coaching in Lucknow. We are one of the Leading NDA Coaching Institutes in Lucknow. if you are looking for (National Defence Academy Entrance exam) preparation then PFDA is one of the best Defence Coaching in Lucknow.

Our Defence Academy offers the best coaching for the NDA written examinations. We are a Best NDA Coaching in Lucknow, we are also known as Best NDA training Institutes in Lucknow. Our faculty is highly qualified and vastly experienced in successfully coaching students for NDA examinations.

Are you tired of searching here for getting Best NDA Coaching Classes in Lucknow? Did you find the right institute that can provide your classes for NDA coaching in Lucknow so that you can crack the NDA exam and get admission to the prestigious Army, Navy and Air force for serving India? If not, then no need to worry anymore because Pathfinder Defence Academy is here for your help by providing the top-level and advanced level of coaching classes with experienced faculties.

PathFinder Defence Academy is considered as the most effective institution for NDA aspirants as we provide one of the Best Coaching and Training in Lucknow. We have one of the best faculties for providing professional training of the highest quality. We have set the standards of excellence in NDA Coaching through our detailed and quality training conducted by the best teachers. Our course covers the entire NDA Syllabus as set by the UPSC.

Pathfinder Defence Academy is a top institute for NDA Coaching in Lucknow. This Academy offers the Best Coaching Classes for NDA written Exam. And Pathfinder Defence Academy provides you with a better opportunity to crack your goal and join the Indian Defence Services. The Faculty of Pathfinder defense is highly skilled and qualified in coaching.

Pathfinder Defence Academy offers the No-1 coaching for NDA written exams in Lucknow. This Institute totally focused on the student’s aim and objective of candidates. And we complete the whole course and syllabus of the NDA written exam in accordance with, Union Public Service Commission (UPSC) before the examination. We organized the mock tests and Group Discussions from time to time we prepared our as per previous year question paper tests and we provide the doubt clearing classes every week. And results of weekly mock tests are also reviewed.

Pathfinder Defence Institute Best For NDA Coaching in Lucknow offers coaching Center for defense exam preparation like NDA exam 2019-2020, leading coaching classes in Lucknow for NDA exam 2018, Join Pathfinder Defence Academy for best guidance and preparation and result in Defence Exam

ELIGIBILITY CRITERIA

Nationality: Apart from Indian origin, candidates from other countries can also appear for NDA 2019 Candidates must either be.

India citizen.

Citizen of Bhutan.

Citizen of Nepal.

Tibetan refugee who came over to India before January 1, 1962, with the intention of permanently settling in India.

Indian origin person migrated from Pakistan, Burma, Sri Lanka and East African Countries of Kenya, Uganda, the United Republic of Tanzania, Zambia, Malawi, Zaire, and Ethiopia or Vietnam with the intention of permanently settling in India.

AGE LIMITS

Nationality: Apart from Indian origin, candidates from other countries can also appear for NDA. Candidates must either be.

Minimum Age: 15-1/2 years. (For Form Filling)

Maximum Age: 18-1/2 years. (For Form Filling)

The date of birth will be calculated as it is entered in the Matriculation or Secondary School Leaving Certificate or in a certificate recognized by an Indian University as equivalent to Matriculation.

Marital Sex: Candidates must be unmarried.

Gender: Only male candidates are eligible to apply for NDA.

EDUCATIONAL QUALIFICATION

Army Wing of Pathfinder Defence Academy: Candidates applying for the Indian Army must have passed class 12/HSC in 10+2 pattern of School Education or equivalent examination conducted by a State Education Board or a University.

Air Force, Navy and Naval Academy of PathFinder Defence Academy: Candidates applying for Air Force, Navy and Naval Academy must have passed class 12/HSC in 10+2 pattern of School Education with Physics and Mathematics conducted by a State Education Board or a University.

Physical standard required for NDA: Candidates appearing in NDA must be physically and mentally fit according to the prescribed physical standards. A candidate recommended by the Services Selection Board (SSB) will undergo a medical examination by a Board of Service Medical Officers. Only those candidates will be declared qualified NDA and admitted to the academy who is declared fit by the medical board. The candidate must be in good physical and mental health and free from any disease/disability which is likely to interfere with the efficient performance of military duties. The minimum acceptable height is 157 cm for Army, Navy and Naval Academy while 162.5 cm for Air Force. For Gurkhas and individuals belonging to hills of North-Eastern, the minimum acceptable heights will be 5 cm less. For more detail required physical standards candidates are advised to read the NDA notification.

SYLLABUS

Paper-I Mathematics (Maximum Marks – 300) :

Algebra: Concept of set, operations on sets, Venn diagrams. De Morgan laws. Cartesian product, relation, equivalence relation. Representation of real numbers on a line. Complex numbers – basic properties, modulus, argument, and cube roots of unity. Binary system of numbers. Conversion of a number in decimal system to binary system and vice-versa. Arithmetic, Geometric and Harmonic progressions. Quadratic equations with real coefficients. The solution of linear inequations of two variables by graphs. Permutation and Combination. Binomial theorem and its application. Logarithms and their applications.

Matrices and Determinants: Types of matrices, operations on matrices Determinant of a matrix, basic properties of determinant. Adjoint and inverse of a square matrix, Applications – Solution of a system of linear equations in two or three unknowns by Cramer’s rule and by Matrix Method.

Trigonometry: Angles and their measures in degrees and in radians. Trigonometrically ratios. Trigonometric identities Sum and difference formulae. Multiple and Sub-multiple angles. Inverse trigonometric functions. Applications – Height and distance, properties of triangles.

Analytical Geometry of two and three dimensions: Rectangular Cartesian Coordinate system. Distance formula. Equation of a line in various forms. The angle between the two lines. The distance of a point from a line. Equation of a circle in standard and in general form. Standard forms of parabola, ellipse, and hyperbola. Eccentricity and axis of a conic. The point in a three-dimensional space, distance between two points. Direction Cosines and direction ratios. Equation of a plane and a line in various forms. The angle between the two lines and the angle between the two planes. Equation of a sphere.

Differential Calculus: Concept of a real-valued function – domain, range, and graph of a function. Composite functions, one to one, onto and inverse functions. Notion of limit, Standard limits – examples. Continuity of functions – examples, algebraic operations on continuous functions. Derivative of a function at a point, geometrical and physical interpretation of a derivative – applications. Derivatives of sum, product, and quotient of functions, a derivative of a function with respect of another function, derivative of a composite function. Second-order derivatives. Increasing and decreasing functions. Application of derivatives in problems of maxima and minima.

Integral Calculus and Differential equations: Integration as inverse of differentiation, integration by substitution and by parts, standard integrals involving algebraic expressions, trigonometric, exponential and hyperbolic functions. Evaluation of definite integrals �� determination of areas of plane regions bounded by curves – applications. Definition of order and degree of a differential equation, formation of a differential equation by examples. General and particular solution of a differential equation, solution of the first order and first-degree differential equations of various types – examples. Application in problems of growth and decay.

Vector Algebra: Vectors in two and three dimensions, magnitude and direction of a vector. Unit and null vectors, the addition of vectors, scalar multiplication of vector, scalar product or dot product of two vectors. Vector product and cross product of two vectors. Applications-work did by a force and moment of a force, and in geometrical problems.

Statistics and Probability:

Statistics: Classification of data, Frequency distribution, cumulative frequency distribution – examples Graphical representation – Histogram, Pie Chart, Frequency Polygon – examples. Measures of Central tendency – mean, median and mode. Variance and standard deviation – determination and comparison. Correlation and regression.

Probability: Random experiment, outcomes, and associated sample space, events, mutually exclusive and exhaustive events, impossible and certain events. Union and Intersection of events. Complementary, elementary and composite events. Definition of probability – classical and statistical – examples. Elementary theorems on probability – simple problems. Conditional probability, Bayes’ theorem – simple problems. Random variable as function on a sample space. Binomial distribution, examples of random experiments giving rise to Binominal distribution.

PAPER-II

General Ability Test (Maximum Marks-600)

PART – A

ENGLISH (Maximum Marks 200).

The question paper in English will be designed to test the candidate’s understanding of English and workmanlike use of words. The syllabus covers various aspects like Grammar and usage, vocabulary, comprehension, and cohesion in extended text to test the candidate’s proficiency in English.

PART – B

SYLLABUS OF PHYSICS

Physical properties and states of matter. Mass Weight, Volume, Density, and Specific Gravity, Principle of Archimedes, Pressure Barometer.

The motion of objects: Velocity and acceleration. Newton’s Laws of motion. Force and Momentum. Parallelogram of Forces. Stability and equilibrium of bodies. Gravitation, elementary ideas of work, Power and Energy.

Effects of heat: Measurement of temperature and heat. Change of state and latent heat. Modes of transference of heat. Sound Waves and their properties. Simple musical instruments. Rectilinear propagation of light. Reflection and Refraction. Spherical mirrors and lenses. Human eye.

Natural and artificial magnets: properties of a magnet. Earth as a magnet.

Static and current electricity: Conductors and non-conductors. Ohm’s law. Simple electrical circuits. Heating, lighting and magnetic effects of current. Measurement of electrical power. Primary and Secondary Cells. Use of X-rays.

General principles in the working of the following: Simple pendulum, Simple Pulleys, Siphon, Levers, Balloon. Pumps, Hydrometer, Pressure Cooker, Thermos Flask, Gramophone, Telegraphs. Telephone, Periscope, Telescope, Microscope, Mariner's Compass, Lightning Conductors and Safety Flues.

Syllabus of General Science :

Basis of Life – Cells, Protoplasms and Tissues, Elementary knowledge of human body and its important organs, Food – Source of Energy for man, Constituents of food, Balanced Diet, Achievements of Eminent Scientists, Difference between the living and non-living, Growth and Reproduction in Plants and Animals, Common Epidemics, their causes and prevention, The Solar System – Meteors and Comets, Eclipse.

History: Freedom Movement in India, elementary knowledge of five-year plans of India, Bhutan, Sarvodaya, National Integration and Welfare State, Basic Teachings of Mahatma Gandhi, A broad survey of Indian History, with emphasis on Culture and Civilisation, Elementary study of Indian Constitution and Administration, Panchayati Raj, Co-operatives and Community Development, Forces shaping the modern world; Renaissance, Exploration, and Discovery; War of American Independence. French Revolution, Industrial Revolution, and the Russian Revolution. Impact of Science and Technology on Society. Concept of one World, United Nations, Panchsheel, Democracy. Socialism and Communism. Role of India in the present world.

Geography: Origin of Earth, Rocks, and their classification; Weathering – Mechanical and Chemical, Earthquakes and volcanoes, Atmosphere and its composition; Temperature and Atmospheric Pressure, Planetary Winds, cyclones, and Anti-cyclones; Humidity; Condensation and Precipitation; Types of Climate. Major Natural regions of the World, Important Sea ports and main sea, land, and air routes of India. Main items of Imports and Exports of India, The Earth, its shape and size. Lattitudes and Longitudes, Concept of time, International Date Line, Movements of Earth and their effects, Ocean Currents and Tides, Regional Geography of India – Climate, Natural vegetation. Mineral and Power resources; location and distribution of agricultural and industrial activities.

Current Events: Current important world events, Knowledge of Important events that have happened in India in recent years, prominent personalities – both Indian and International including those connected with cultural activities and sports.

#nda #nda coaching #coaching classes

0 notes

rafi1228 · 6 years ago

Link

Learn everything from Algebra 1 and Algebra 2, then test your knowledge with 1,300+ practice questions

What you’ll learn

Operations, including order of operations (PEMDAS) and like-terms

Fractions, exponents, and radicals, including advanced operations with all three

Equations and systems of equations, including inverse operations, direct and inverse variation, and distance/rate/time problems

Graphing, including parallel and perpendicular lines, and parabolas

Polynomials and factoring, including the quadratic formula and completing the square

Functions, including domain and range, and sums and products of functions

Inequalities, including trichotomy and graphing inequalities and conjunctions on a number line

Exponential and logarithmic functions, including laws of logs, change of base, and graphing

Requirements

You should be comfortable with arithmetic (addition, subtraction, multiplication, division) of whole numbers.

You should be comfortable with arithmetic of decimals, fractions, exponents, and radicals.

We’ll start the course with basic algebraic operations, so if you know those arithmetic basics, you’ll be well prepared for the course.

Description

HOW BECOME AN ALGEBRA MASTER IS SET UP TO MAKE COMPLICATED MATH EASY:

This 473-lesson course includes video and text explanations of everything from Algebra, and it includes 125 quizzes (with solutions!) and an additional 21 workbooks with extra practice problems, to help you test your understanding along the way. Become an Algebra Master is organized into the following sections:

Operations and rules of equations

Simple equations and advanced equations

Like terms

Functions and manipulating functions

Inequalities and graphing inequalities

Graphing points, lines, parabolas, and circles

Systems of two equations and systems of three equations

Polynomials and factoring

Exponents and radicals

Ratio and proportion, complex fractions, and rational expressions

Imaginary numbers

Exponential and logarithmic functions

AND HERE’S WHAT YOU GET INSIDE OF EVERY SECTION:

Videos: Watch over my shoulder as I solve problems for every single math issue you’ll encounter in class. We start from the beginning… I explain the problem setup and why I set it up that way, the steps I take and why I take them, how to work through the yucky, fuzzy middle parts, and how to simplify the answer when you get it.

Notes: The notes section of each lesson is where you find the most important things to remember. It’s like Cliff Notes for books, but for math. Everything you need to know to pass your class and nothing you don’t.

Quizzes: When you think you’ve got a good grasp on a topic within a course, you can test your knowledge by taking one of the quizzes. If you pass, great! If not, you can review the videos and notes again or ask for help in the Q&A section.

Workbooks: Want even more practice? When you’ve finished the section, you can review everything you’ve learned by working through the bonus workbook. The workbooks include tons of extra practice problems, so they’re a great way to solidify what you just learned in that section.

HERE’S WHAT SOME STUDENTS OF BECOME AN ALGEBRA MASTER HAVE TOLD ME:

“Thank you Krista for making this so clear and understandable! You are a fantastic tutor. A+++” – Omid N.

“At the peak of my mathematical skill level I reached only into the very early stages of learning Trigonometry. Fast forward to now (my early 30’s) and by experience alone, realize the infinite possibilities of being a master in mathematics. I chose Ms. King’s Algebra course as a review to move past my previous level and must say that I not only ENJOY the course she offers but am getting more from it learning wise than I could have imagined. I wish to complete all of her classes and am extremely confident that her teaching style can get me there. Other than mere reference of other resources, I plan to stay on track with all of Ms. King’s courses exclusively. Thank you for a great learning experience!” – Dean F.

“Great! I love how she teaches!” – Fred B.

“The instructor is very clear, both in ideas and in speech. She moves quickly enough to keep your attention, but not so that you get lost.” – Janet M.

“I have been enrolled in several Udemy courses but this course is the best. It’s my first time posting a review because I am really happy with how Krista King teaches mathematics. One of the best courses on Udemy.” – Salahuddin S.

“This course is awesome. She explains everything perfectly. And if you want you can complete a test after every video to make sure you understand everything. I strongly recommend it.” – Rafael N.

“The sessions are well planned. Exercises are done at the right times to help consolidate what you have learned during the sessions. Definitely the best math course I have taken. The instructor has done an awesome job with this one.” – Eduardo C.

“The instructor’s delivery is clear and engaging. The pacing is effective and the quizzes serve to reinforce the knowledge as I learn it.” – Jeremiah P.

YOU’LL ALSO GET:

Lifetime access to Become an Algebra Master

Friendly support in the Q&A section

Udemy Certificate of Completion available for download

30-day money back guarantee

Enroll today!

I can’t wait for you to get started on mastering algebra.

– Krista 🙂

Who this course is for:

Current Algebra 1 and Algebra 2 students, or students about to start algebra who are looking to get ahead

Homeschool parents looking for extra support with algebra

Anyone who wants to study math for fun after being away from school for a while

Created by Krista King Last updated 2/2019 English English [Auto-generated]

Size: 1.90 GB

Download Now

https://ift.tt/1Zktmds.

The post Become an Algebra Master appeared first on Free Course Lab.

#IFTTT #Blogger

0 notes