#set theory

[4denthusiast]

"Average person discovers infinitely many infinities per year" factoid is actually just a statistical error. The average person discovers 0 infinities per year. Cantor Georg, who introduced the diagonal argument and discovered infinitely many infinities in 1891 alone, is an outlier and cannot be counted.

[real-real-numbers]

the first rule of fight club is that two fight clubs are equal if they have the same members

[algebraic-dumbass]

"i have 99 problems" lame. "i have an amount of problems strictly in between aleph0 and the cardinality of the continuum" exciting. takes a stance on the continuum hypothesis

[pv1isalsoimportant]

Mathematical platonists are so funny to me because they will say shit like "mathematics has this beautiful elegant design" meanwhile you get to the foundations and find out you have those "beautiful elegant statements" that are independent of ZF (or even ZFC), are not compatible with each other and each of them implies some insane monstrosity that shouldn't ever be true.

[catgirl-lucy]

Ultrafilters & Ultrapowers

Hey! Call me Lucy. I might make an introduction blog later, but I first wanted to make a blog-post about ultrapowers.

Ultrafilters are a concept from set theory, I'll try my best to explain what they are and why they're defined as they are.

First, a quick overview of what we will do: we will extend the real number line by adding new numbers through the use of an ultrapower, these new numbers are called "hyperreals". Roughly, this means that we will have infinite sequences [a₀,a₁,a₂,...] of real numbers representing hyperreal numbers, where similar sequences are regarded as equal. We will also show a surprising theorem: although there are seemingly more hyperreals than reals, hyperreals look the same as real numbers "from within".

If we have a sequence of reals like this: [0,1,1/2,1/3,1/4,...] (I'll call this sequence "ε"), the hyperreal that it represents can be viewed as the "limit" of the sequence. Since a large number of entries of this sequence is smaller than any positive real number r > 0, ε will be smaller than any positive real number r, but since also a large number of entries is larger than 0, ε will be larger than 0. ε is thus an infinitesimal hyperreal number. This is mostly just intuition though, so don't worry if you don't entirely get it.

Two hyperreal numbers x = [x₀,x₁,x₂,...] and y = [y₀,y₁,y₂,...] are equal if x_i = y_i for a large number of indices i. But what does "large" mean in this context?

Well, that's where the ultrafilter comes in. Ultrafilters split a family of sets into sets that are "large" and sets that are "small". In this case, we split sets of natural numbers (numbers 0, 1, 2, 3, etc) into large sets and small sets, so we have an ultrafilter on ℕ, the set of natural numbers. Ultrafilters are identified by the family of large sets: if some set A is in an ultrafilter U, then it is large, and if it's not, then it is small.

We do want our notion of "large sets" and "small sets" to make sense: for example, a hyperreal should always be equal to itself, so we want the whole set of natural numbers, {0, 1, 2, 3, 4, ...} (which is the set of indices for which a sequence is equal to itself), to be large.

Obviously, it would make sense that if a set A is large and B is larger than A, then B is also large. Thus, if A ∈ U is a member of an ultrafilter U ("∈" is the membership symbol), and if B ⊃ A contains everything A contains too ("⊃" is the superset symbol), then B ∈ U is a member of the ultrafilter as well.

We also want hyperreal equality to be transitive, thus if [x₀,x₁,x₂,...] = [y₀,y₁,y₂,...] and [y₀,y₁,y₂,...] = [z₀,z₁,z₂,...], then we want [x₀,x₁,x₂,...] = [z₀,z₁,z₂,...]. If A = {i ∈ ℕ | x_i = y_i} is the set of points at which x and y are equal and B = {i ∈ ℕ | y_i = z_i} is the set of points at which y and z are equal, then C = {i ∈ ℕ | x_i = z_i}, the set of points at which x and z are equal, includes the set A ∩ B = {i ∈ ℕ | x_i = y_i ∧ y_i = z_i}, the set of points at which x is equal to y and y is equal to z. It thus makes sense to have our ultrafilter be closed under intersections: if two sets A and B are large, then the set of points that are both in A and in B, called the "intersection" of A and B (denoted A ∩ B), is a large set as well (and thus also in the ultrafilter).

It would also make sense that, if two hyperreal numbers are nowhere equal, then they aren't equal. So the empty set, {} = ∅, is small.

The five axioms above describe a filter:

A filter F on κ is a family of subsets of κ.

A filter F on κ must contain the whole set κ.

A filter F on κ must be upwards closed, thus for every large set A ∈ F, and every larger set B ⊃ A, B ∈ F is large as well.

A filter F on κ must be downwards directed, thus for every large set A ∈ F and every large set B ∈ F, the intersection of A and B, A ∩ B ∈ F, is large as well.

A filter F on κ may not contain the empty set.

However, these are the axioms of a filter, and not of an ultrafilter. Ultrafilters have one additional axiom.

Suppose we have the hyperreal [0,1,0,1,0,1,...]: an alternating sequence of 0's and 1's. Is this equal to 0 = [0,0,0,0,...], or to 1 = [1,1,1,1,...], or is it its own thing? (Note: the 0 in 0 = [0,0,0,0,...] is a hyperreal and the 0's in 0 = [0,0,0,0,...] are real numbers, so they're different (kind of) numbers both called "0"). If it is its own thing, then is it smaller than 1? If it is smaller than 1, then it must be smaller on a large set of indices, meaning it's equal to 0 on a large set of indices, meaning it's equal to 0. If it's not smaller than 1, well, it can't be larger, so it'd only make sense if it's equal to 1, but no axiom about filters says it should! That's why we have this last axiom for ultrafilters, which makes them "decisive": for every set A, it is either large (thus, A ∈ U), or small, meaning that its complement, Ac = {i | i ∉ A}, the set of all points that aren't in A, is large.

And so we have our six axioms of an ultrafilter:

An ultrafilter U on κ is a family of subsets of κ, these subsets are called "large sets".

κ is large.

U is upwards closed.

U is downwards directed.

∅ is not large.

For every set A ⊂ κ, either A ∈ U or Ac ∈ U.

But we're still missing one thing. We can take our ultrafilter U to be the set of all sets of natural numbers that contain 6. ℕ is large, as it contains 6. It is upwards closed: if A contains 6 and B contains everything that A contains and more, then B also contains 6. U is downwards directed: if both A and B contain 6, then the set of all points that are in both A and B still contains 6. The empty set does not contain 6, and every set either does contain 6 or does not contain 6. With this ultrafilter, two hyperreals x and y are equal simply when x₆ and y₆ are equal, so we don't get cool infinitesimals and infinities, and that makes me sad :(

These kinds of boring ultrafilters are called principal ultrafilters. Formally, a principal filter on κ is a filter F on κ for which there is some set X ⊂ κ so that any set A ⊂ κ is large only if it contains everything in X. This filter is often denoted as ↑X. If you want a principal filter U to be an ultrafilter, X needs to be a singleton set, meaning it only contains a single point x. Proving this is left as an exercise for the reader.

Let U be a non-principal ultrafilter on ℕ. This post is getting a bit long, so I won't show why such an ultrafilter exists. Now, we can take the ultrapower of ℝ, the set of real numbers, by U. This ultrapower is often denoted as ℝ^ℕ/U. Members of this ultrapower are (equivalence classes of) functions from ℕ to ℝ, meaning that they send natural numbers/indices to real numbers (the sequence [x₀,x₁,x₂,...] maps the natural number i to the real number x_i). These functions/sequences/equivalence classes are called hyperreal numbers. Two hyperreal numbers, x and y, are equal if {i ∈ ℕ | x(i) = y(i)}, the set of points at which they are equal, is large (i.e. a member of U). We can also define hyperreal comparison and arithmetic operations: x < y if {i | x(i) < y(i)} is large, (x + y)(i) = x(i) + y(i) and (x · y)(i) = x(i) · y(i). Every real number r also has a corresponding hyperreal j(r), which is simply [r,r,r,r,...] (i.e. j(r)(i) = r for all i).

In general, if M is some structure, κ is some set and U is some ultrafilter on κ, then we can take the ultrapower M^κ/U, which is the set of equivalence classes of functions from κ to M, where any relation R in M (for example, "<" in ℝ) is interpreted in M^κ/U as "R(x₁,...,xₙ) if and only if {i ∈ κ | R(x₁(i),...,xₙ(i))} ∈ U is large" and any function f in M (for example, addition in ℝ) is interpreted in M^κ/U as "f(x₁,...,xₙ)(i) = f(x₁(i),...,xₙ(i)) for all i ∈ κ".

A quick note on equivalence classes: in M^κ/U, points aren't actually functions from κ to M, but rather sets of functions from κ to M that are all equal on a large set of values. Given a function f: κ → M, the equivalence classes that f is in is denoted [f]. In this way, if f and g are equal on a large set of values, then [f] and [g] are actually just equal.

The hyperreal [0,1,2,3,4,...], which sends every natural number i to the real number i, is often called ω.

This part of the blog will get a bit more technical, so be warned!

In the beginning of this blog-post, I mentioned that hyperreals look the same as real numbers. I'll make this statement more formal:

For any formula φ that can be built up in the following way:

φ ≡ "x = y" for expressions x and y (expressions are variables and "a + b" and "a · b" for other expressions a and b)

φ ≡ "x < y" for expressions x and y

φ ≡ "ψ ∧ ξ" (ψ and ξ are both true) for formulas ψ and ξ

φ ≡ "ψ ∨ ξ" (ψ or ξ is true (or both)) for formulas ψ and ξ

φ ≡ "¬ψ" (ψ is not true) for an formula ψ

φ ≡ "∃x ψ(x)" (there exists a value for x for which ψ is true) for a variable x and an formula ψ

φ ≡ "∀x ψ(x)" (for all values of x, ψ is true) for a variable x and an formula ψ

We have that ℝ ⊧ φ (φ is true when evaluating equality, comparison and expressions from within ℝ, where variables can have real number values) if and only if ℝ^ℕ/U ⊧ φ (φ is true when evaluating equality, comparison and expressions from within ℝ^ℕ/U, where variables can have hyperreal number values).

In other words: ℝ and ℝ^ℕ/U are elementary equivalent.

So, how will we prove this? Well, we will use induction: "if something being true for all m < n implies it being true for n itself, then it must be true for all n (where m and n are natural numbers)". Specifically, we will use induction on the length of formulas: we will show that, if the above statement holds for all formulas ψ shorter than φ, then it must also hold for φ.

However, we won't use the exact statement above. Instead, we will use the following:

Given a formula φ(...) and hyperreal numbers x₁,...,xₖ, ℝ^ℕ/U ⊧ φ(x₁,...,xₖ) if and only if {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} is large.

Now, why does this imply the original statement? Well, when k = 0, {i | ℝ ⊧ φ} can only be ∅ or ℕ. It being ∅ is equivalent to φ being false in ℝ and, if the statement is true, also equivalent to φ being false in ℝ^ℕ/U. And it being ℕ is equivalent to φ being true in ℝ and, again, if the statement is true, it is also equivalent to φ being true in ℝ^ℕ/U. We thus have that φ being true in ℝ is equivalent to φ being true in ℝ^ℕ/U.

Note: M ⊧ φ simply means that the formula φ is true when interpreted in M.

Now, why do we need this stronger statement? Well, it makes induction a lot easier: given that this statement holds for all ψ shorter than φ, it's easier to prove it also holds for φ.

Now, we can actually do the induction.

First, if φ ≡ "x = y", then we need to show that (1) ℝ^ℕ/U ⊧ φ(x,y) iff (2) {i | ℝ ⊧ φ(x(i),y(i))} is large. This follows immediately from the definition of equality in ℝ^ℕ/U, the same holds for "<".

Now, if φ(x₁,...,xₖ) ≡ "ψ(x₁,...,xₖ) ∧ ξ(x₁,...,xₖ)", we have that {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i)) ∧ ℝ ⊧ ξ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i))} ∩ {i | ℝ ⊧ ξ(x₁(i),...,xₖ(i))}. Since {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i))} is large iff ψ(x₁,...,xₖ) is true in ℝ^ℕ/U, and {i | ℝ ⊧ ξ(x₁(i),...,xₖ(i))} iff ξ(x₁,...,xₖ) is true in ℝ^ℕ/U, and U is closed under intersections, we have that {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} is large iff φ holds in ℝ^ℕ/U. A similar argument works for ∨.

If φ(x₁,...,xₖ) ≡ "¬ψ(x₁,...,xₖ)", then we can just use the ultraness of the ultrafilter.

If φ ≡ "∃y ψ(y,x₁,...,xₖ)", then {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ∃y ψ(y,x₁(i),...,xₖ(i))} = {i | ∃y ∈ ℝ. ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} = ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))}. We have that the set {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} for y ∈ ℝ is large iff ℝ^ℕ/U ⊧ ψ(j(y),x₁,...,xₖ). If this set is large for some y ∈ ℝ, and thus if ℝ^ℕ/U ⊧ φ(x₁,...,xₖ), then ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} is larger than that set, so it is large as well. For the converse direction, if ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} is large, then we can create a hyperreal z where ψ ⊧ ψ(z(i),x₁(i),...,xₖ(i)) for all i for which ℝ ⊧ ∃y ψ(y,x₁(i),...,xₖ(i)), and we have ℝ^ℕ/U ⊧ ψ(z,x₁(i),...,xₖ(i)), and thus ℝ^ℕ/U ⊧ φ(x₁(i),...,xₖ(i)). Again, a similar argument works for ∀.

(Sorry if you couldn't follow along, I'm not good at explaining these things in an intuitive way.)

This result can be extended to show that M^κ/U is elementary equivalent to M for every structure M, every set κ and every ultrafilter U on κ.

Now, this result might be surprising, as we have a new number ω in ℝ^ℕ/U. Surely, there is a formula that states the existence of this number, right?

Well, it turns out, such a formula does not exist! You can try something like "there is no natural number n so that 1+...+1 w/ n 1's is greater than ω", but ω+1 is a natural number in the hyperreals, so such a natural number does exist. Similarly, any formula you can come up with, as long as it is created using the rules above (using conjunction, disjunction, negation, qauntification, etc), cannot state the existence of an infinite number ω.

But if ℝ^ℕ/U and ℝ are seemingly indistinguishable, might there already be an undetectable infinite real number in ℝ? Well, maybe~ :3 But it's undetectable anyways, so you don't have to worry about it.

Before I end this blog-post, I want to give some more intuition on what filters & ultrafilters actually are. To me, ultrafilters, and filters in general, are like "limits of sets". The principal filter ↑X has X as limit, while non-principal filters and ultrafilters have limits that aren't really sets, but look like ones. For example, you might have the set of prime numbers in your filter, and then the limit of that filter will be a "set" in which all numbers are prime numbers. And if your ultrafilter is non-principal (so for every n, there is a set A ∈ U in the filter that does not contain n), then the limit of that ultrafilter will be a "set" in which all numbers don't actually exist. In the case of filters, this "set" can be any "set" (though it still isn't really a set), but in the case of ultrafilters, this limit looks like a singleton set (i.e. it only has one "element": ω).

I don't know if my intuition of filters and ultrafilters will help anyone, tho, but I think it's cool!

That's all I had to say.

Bye!~ Have a nice day.

[lilith-hazel-mathematics]

Self-referencing functions

Hey mathblr, let me tell you about one of our favorite foundational systems for mathematics! It's designed to allow for unlimited self-reference, which is neat since self-reference is usually thought of as a big no-no in foundational systems. It turns out that it actually doesn't matter at all, because the power of self-reference is completely exhausted by the partial computable functions. The theory ends up being equivalent to Peano Arithmetic.

What are the axioms?

The theory is two-typed: the first type is for the natural numbers, and the second type is for functions between numbers. For convenience, numbers will be represented by lowercase variables, and uppercase variables represent functions. To prevent logical contradictions, we permit that some functions will fail to evaluate, so we include a non-number object ☒ called "null" for such cases. The axioms about numbers are basically what you'd expect, and we only need one axiom about functions.

The < relation is a strict total order between numbers.

Each nonempty class has a minimum: axiomatize the "min" operator with φ(n) ⇒ ∃m,(φ(m) ∧ min{k:φ(k)}=m≤n) for each predicate φ, and relatedly min{k:φ(k)}=☒ ⇔ ∀n, ¬φ(n).

Numbers exist: ∃n,n=n

There's no largest number: ∀n,∃k,n

There's no infinite number: ∀n,n=0 ∨ ∃k,n=S(k)

Every functional expression represents a function object that exists: ∃F, ∀(a,b,c), F(a,b,c)=Ψ for any function term Ψ. The term Ψ may mention F.

To clarify the fifth axiom, we define 0:=min{n : n=n}, and relatedly S(k):=min{n : k<n} is the successor function. The sixth axiom allows us to construct self-referencing functions using any "function term". Basically, a term is any expression which evaluates numerically. Formally, a "function term" is any well-formed formula generated from the following formation rules.

"n" is a term; any number variable.

"F(Θ,Φ,Ψ)" is a term, whenever Θ,Φ,Ψ are terms.

"Φ<Ψ" is a term, whenever Φ,Ψ are terms.

"min{n : Ψ}" is a term, whenever Ψ is a term.

In the third rule, we seem to be using the boolean relation < as if it were a numerical operator. To clarify this, we use the programmer convention that true=1 and false=0, hence (n<k)=1 whenever n<k is true, and otherwise it's zero. Similarly in the fourth rule, when we use the numerical function term Ψ as the argument to the "min" operator, we interpret Ψ as being false whenever it's 0, and true whenever it's positive. Formally, we can use the following definitions.

(n<k) = min{b : k=0 ∨ ((n<k ⇔ b=1) ∧ n≠☒≠k)} min{n : Ψ(n)} = min{n : 0<Ψ(n) ∧ ∀(k<n),Ψ(k)=0}

Okay, what can it do?

The formation rules on functions actually gives us a TON of versatility. For example, the "<" relation can be used to encode literally all boolean logic. Here's how you might do that.

¬x = (x<1) (x≤y) = ¬(y<x) x⇒y = (¬¬x ≤ ¬¬y) x∨y = (¬x ⇒ y) x∧y = ¬(¬x ∨ ¬y) (x=y) = ((x≤y)∧(y≤x)) [p?x:y] = min{z : (p∧(z=x))∨(¬p∧(z=y))}

That last one is the ternary conditional operator, which can be used to implement casewise definitions. If you wanna get really creative, you can implement bounded quantification as an operator, which can then be used to define the supremum/maximum operator!

∃[t<x, F(t)] = (min{t : t=x ∨ ¬F(t)}<x) ∀[t<x, F(t)] = ¬∃[t<x, ¬F(t)] sup{F(t) : t<x} = min{y : ∀[t<x, F(t)≤y]}

Of course, none of this is even taking advantage of the self-reference that our rules permit. For example, we could implement addition and multiplication using their recursive definitions, provided we define the predecessor operation first. Alternatively, we can use the supremum operator as a little shortcut.

x+y = [y ? sup{succ(x+t) : t<y} : x] x*y = sup{(x*t)+x : t<x} x^y = [y ? sup{(x^t)*x : t<y} : 1]

Using the axioms we established, basically as a simple induction, it can be proved that these operations are total and obey their ordinary recursive definitions. So, our theory is at least as strong as Peano Arithmetic. It's not hard to believe that our functions can represent any partial computable function, and it's only a little harder to prove it formally. Conversely, all our axioms are true when restricted to the domain of partial computable functions, so it's consistent that all our functions are computable. In particular, there's a straightforward way to interpret each function term as a computer program. Since PA can quantify over computable functions, our theory is exactly as strong as PA. In fact, it's basically just a definitorial extension of PA. Pretty neat, right?

Set theory jumpscare

Hey didn't you think it was weird how we never asserted the axiom of induction? We asserted wellfoundedness with the minimization operator, which is basically equivalent, but we also had to deny infinite numbers for induction to work. What if we didn't do that? What if we did the opposite? Axiom of finity unfriended, our domain of discourse is now the ordinal numbers. New axioms just dropped.

There's an infinite number: ∃w, 0≠w ∧ ∀k, S(k)≠w

Supremums: (∀(x≤a),∃y,φ(x,y)) ⇒ ∃b,∀(x≤a),∃(y≤b),φ(x,y)

Unlimited Cardinals: ∀a, ∃b, #(a)<#(b), where #(n) denotes the cardinality operation.

Each of the above axioms basically just assert the existence of larger and larger ordinal numbers, continuing the pattern set out by the third and fourth axioms from before. Similar to how the previous theory could represent all computable functions, this theory can represent all the ordinal recursive functions. These are the functions which are representable using an Ordinal Turing Machine (OTM). Conversely, it's consistent that all functions are ordinal recursive, since each function term can be interpreted as a program that's executable by an OTM. Moreover, just like how the previous theory was exactly as strong as PA, this theory is exactly as strong as ZFC.

It takes a lot of work to interpret ZFC, but basically, a set can be represented by its wellfounded and extensional membership graph. The membership graphs can, in turn, be encoded by our ordinal recursive functions. Using the Supremums axiom, it can be shown that the resulting universe of sets obeys a version of the Axiom of Replacement, which can be used to prove the Reflection Theorems, ultimately leading to the Specification Axiom. By adapting similar techniques relative to some regular cardinal, it can then be shown that every set admits a powerset. Lastly, since our functions are basically generated from infinitary computer code, they can be encoded by finite strings having ordinal numbers as symbols. Those finite strings are wellorderable, which induces a global choice function, proving the Axiom of Choice. Excluding a few loose ends, this covers all the ZFC axioms, giving the desired interpretation.

In the finitistic version of this theory, we made the observation that the theory was basically just a definitorial expansion of PA. In the infinitary case however, we unfortunately cannot say the same about ZFC. This ultimately comes down to the fact that our theory provides explicit and definable choice functions, meanwhile ZFC cannot. Although ZFC guarantees that choice functions exist, it cannot prove the existence of a definable choice function. This is because ZFC is an inferior theory has no clue where its sets come from, or what they really look like. Our theory, built from unlimited self-reference, and interpreted under the banner of ordinal recursive functions, is instead equivalent to the theory ZFC+"V=L".

[ravings-of-a-mad-scientist]

STE(A)M Meeting

Engineer: What if we added Art to STEM, so it says STEAM? Like a STEAM ENGINE?

Biologist: but i like stems…

Physicist: Sorry, but STEAM’s got my vote. I approve of all 7(ish?) phases of water. I think.

Computer Scientist: I vote for STEAM too, #PC gaming master race

Set Theorist: I will also vote in favor of increasingly large collections of seemingly unrelated things.

Education Professor: That's all very... dumb. F-. But, I have a pretty good idea on how to use the A so I'll vote for it too!

Biologist: :(

Artist: wtf, why am I here? What kinda nerdy sausage party is this?

Education Professor: (on hands and knees) PLEASE PLEASE PLEASE MAKE OUR CURRICULUMS LESS BORING I DON'T KNOW HOW TO STOP ALL MY STUDENTS FALLING ASLEEP IF THEY CAN'T BE CREATIVE PLEASE

[confusedcanaries]

Set Theory Axioms

Extensionality: What a set is

Empty Set: Oh no we forgot to make a set that definitely exists

Pairing: Why do all our sets only contain one element

Union: But what if I want to ship these sets?

Powerset: But what if I only like a little bit of the set?

Comprehension: Russels Paradox was bad, but also really cool?

Infinity: It would be great if we could do some maths now. Guess we’ll just assume the natural numbers exist

Replacement: I mean infinity isn’t that big, we could give ourselves a little more room

Foundation: We should probably have made sure that all these sets made sense earlier, huh

Choice: This one simple trick might just break everything! A subset of mathematicians hate them!

[m---a---x]

So you people like convoluted diagrams, too?

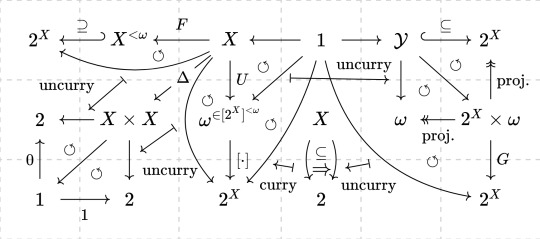
Here ya go, filthy

[more-mathematics-mor-lam]

Explaining to Sauron that the real ring of power is the axiom of choice <=> zorn’s lemma <=> well ordering theorem

[4denthusiast]

I've just noticed an odd combination of beliefs I hold about how maths works. I'm not exactly convinced that every statement in arithmetic (i.e. statements that can be written in terms of 0, the successor function, =, +, ×, and, not, and quantification over natural numbers) is either true or false. (My previously more Platonist views were shaken by some university courses on topics like model theory and Gödel's incompleteness theorems. In order to understand that stuff you have to entertain the possibility that certain seemingly obvious things aren't true, and I then sort of never stopped for some of them.) At the same time, I accept the law of the excluded middle (that P∨¬P is always true). I generally wouldn't describe myself as an intuitinist, even if I am interested in the applications of some intuitionistic logics in computer science.

I think the way I resolve this apparent contradiction is that the reason I don't feel like all arithmetic statements are true or false is that I'm not sure the natural numbers, as a set, are uniquely defined. Any definition of what is and what isn't in ℕ tends to involve some degree of circularity. "It's 0, and S0, and SS0, and so on.", but "so on" for how many steps? A natural number of steps. Hopefully you see the issue. So then, an arithmetic statement may be true of one model of the naturals, but not another. Within any one model, P∨¬P is true (or, more to the point, (∀x. Px)∨¬(∀x. Px) is true), so if it's true in every model it's true, but we can't ever pin down quite which model we're talking about, so the individual statement (∀x. Px) can remain indeterminate.

All this sort of implicitly relies on a separation of the language and meta-language, even though I didn't set out to have a separate meta-language in the first place. I'm not quite sure whether what I'm thinking here even makes sense. Perhaps what I mean is that the meta-language does have logical connectives (and, or, not), so you can form a claim like "(∀x. Px) is true, or ¬(∀x. Px) is true.", but it doesn't have quantification over the naturals, at least not always, because in the meta-language there isn't a unique ℕ, and you can't specify which one you mean because there's no way to totally pin it down. At least I think. But then the semantics of A∨B is meant to be that A∨B is true iff A is true or B is true. I guess we can still recover this by saying that any statement in the language that includes any quantifiers is implicitly with reference to a particular model of ℕ, and a statement is true iff it's true for all models, but then that requires that the meta-language can quantify over models of ℕ, which should be way less possible than quantifying over individual naturals. I don't know how to resolve this, if it even can be resolved. I'm kind of confused.

The true ℕ, if it exists, ought to be the smallest one of course. The trouble is you can't define "smallest" properly without discussing the whole class, which is a less basic concept than the numbers themselves. Also, not every ordered set or class has a smallest element. I think probably if you allow yourself sufficient expressiveness you can prove that in this case there is a smallest (take the intersection or something), but again I don't think you can prove that without making assumptions at least as strong as the conclusion.

The same thing happens with set theory, but there it all feels clearer. In contrast to the naturals where I'm not sure, I feel somewhat more confident that there isn't a single true set-theoretic universe V. There ought to be sets that can't be named (there are only countably many names after all), which makes the universe much trickier to pin down than the naturals. I know there are countable models of ZFC, but they don't feel like they're the real model, and ZFC is itself kind of vague. It leaves a lot of room for rather natural variation in what sets are allowed (e.g. the continuum hypothesis), while non-standard naturals seem much more exotic. If you assume that there's some particular ℕ that's the real ℕ, in the meta-language, this gives you much more solid foundation to use when talking about potential uncertainty in V. You can do induction, talk about constructible sets and stuff. It seems quite likely that the continuum hypothesis doesn't have a definite truth value, even though CH∨¬CH does, but it feels like quite an ordinary sort of indefiniteness, like "He has brown hair." when it isn't clear who "he" refers to. "Is there a cardinal between ω and 2^ω?" What version of the class of cardinals are you talking about?

[dragonessmiralis]

What the fuck would a ∃-Gundam be like? A ∴-Gundam?

Perhaps a a ∪-Gundam, or an ∩-Gundam?

A ∋/:/|-Gundam (why are there so many goddamn ways to write Such That?)

A →-Gundam and its upgrade the ⇒-Gundam

The Natural, Integer, Rational, Irrational, and Real Gundams because tumblr doesn’t let me paste the symbols :(

[then-ponder]

Set theorists what is your preferred set notation?

{Expression : Rule} is the form of{2n : n ∈ ℕ} and is formally expressed as “the set of all thing of the form 2n such that n is an element of ℕ”.

{Rule : Expression} is the form {n ∈ ℕ: 2n} and is formally expressed as “the set of all n in ℕ such that 2n”

[pv1isalsoimportant]

"The proof is simple" this, "the proof is left as an exercise to the reader" that... I do have a specific fondness for "the proof is routine". Like you know very well that the argument will be 2 pages long and technical but on the other hand there's no original thought in the proof and it will be probably one of the 10 arguments this field uses over and over. So like... I believe you. I don't need to know this proof. It IS routine.