#LED cardinal (x1)

[leslie057]

teaming up to do outdoor christmas lights is a great rite of passage for any young couple

[boopiddyboop]

Woodz / Cho Seungyoun Natal Chart Reading

So this is my first natal chart reading about an idol that I barely know. I’ve definitely heard his music (even before X1 came and went) but I’ve not really seen any content of his personality.  So I went to do some research... which led to me getting tickets to see him in December. OOPS. So congrats, anon, ya got me to spend money on your boy.

We’re running with an assumed birthtime of 3 AM, which apparently Seungyoun dropped verbally at some point? I found other websites with this as the cited time, so clearly, the internet never lies  😃

Full Disclaimer: Most of my knowledge is by traditional astrology, which involves but is not limited to: using whole signs, excluding Uranus-Pluto for natal charts, different sign rulers, and different planetary interpretations.  Astrology is subjective by nature; I do not think my way is best, simply that this is the version of interpretation that makes the most sense to me. This is not a professional service, simply a hobby meant for entertainment purposes only.  Feel free to disagree with or question my conclusions.

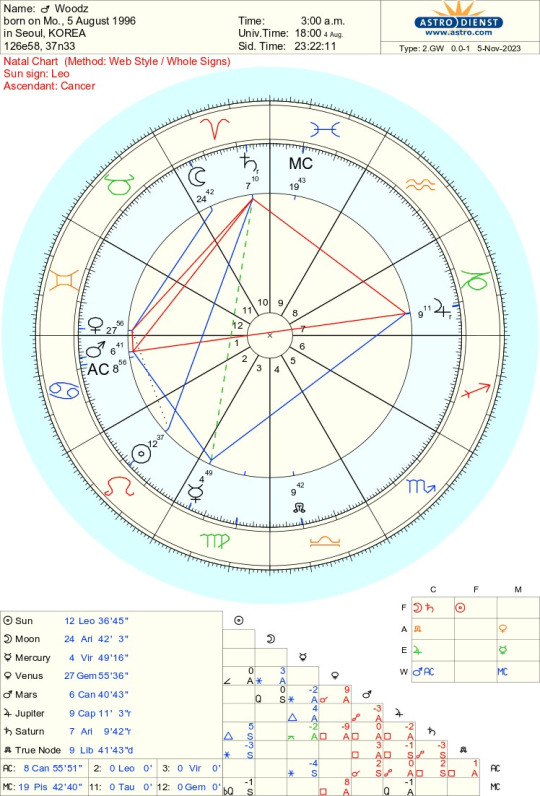
Placements:

Sun: Leo - 2nd House

Moon: Aries - 10th House

Mercury: Virgo - 3rd House

Venus: Gemini - 12th House

Mars: Cancer - 1st House

Jupiter: Capricorn - 12th House

Saturn: Aries - 10th House

Ascendant: Cancer

Midheaven: Pisces - 9th House

North Node: Libra - 4th House

So, Seungyoun is a Cancer Rising being ruled by a Moon in Aries. Now, I love a good fire moon; they bring a sense of playfulness to a chart, especially one in Aries. So for that Moon to the chart ruler… he’s not really understated. And really, when you glance at the composition as a whole, he’s got almost all cardinal and mutable energy. Now, quick refresher: cardinal signs are the starters, and mutable signs are the adaptable ones. Now, I’ve waxed poetic about why I like idols and earth signs, and in some ways that extends to fixed signs. There’s a stubbornness needed to be an idol that both provide, so seeing not a lot of fixed energy had me worried for a bit. Thankfully, his one fixed placement, his Sun in Leo (!! sign in rulership !!), is sitting in his 2nd house, putting a lot of his personal power into achieving material success. Phew. This won’t be the only time Seungyoun’s work ethic gets supported either. 

Mars in the 1st one of these helpful placements, though it’s getting cut off at the knees by being in Cancer, it’s fall sign. Inversely, Cancer rising is a very emotional, artsy placement. Looping back to the rulership by Aries Moon, it leads to someone who is very impulsive and emotionally driven. So when the drive kicks in, it’s powered by that Mars and just goes. Also to not be discounted is his Moon sitting in the 10th house, the house of profession. It gives Seungyoun a lot of emotional investment in his career and a drive to obtain a good reputation in it. 

But once again ~unfortunately~ his Saturn in Aries is also sitting in the 10th house, bringing restrictions and growing pains to this house. I haven’t really touched on Saturn returns (they are both life changing and not as scary as they sound), but there’s a huge potential for his current career to make or break around his return. And that’s about as far as I’ll speculate on that. On the other, other side, that Saturn placement is actually trine his Sun, so once again, he’s getting support to his work ethic through his repeated struggles. Seungyoun has learned what hard work looks like in his life and how to utilize it towards his goals. We should also note that his Jupiter in Capricorn is helping his diligence as well. 

Now that I’ve talked about Seungyoun and his work ethic and career for three paragraphs, let’s switch to different fare. We can see his Mercury in Virgo (!! sign in rulership #2 !!) sitting in his 3rd house, the house of communication. Seungyoun is great at using his words.  Interestingly, I think this Mercury placement ruling his Venus in Gemini is greatly helping his social acumen, which could otherwise be in detriment due to it’s placement in the 12th house. Gemini Venus itself also enjoys quite a diverse range of people, as we can see through the numerous friendships that he is known to have. That Jupiter I mentioned previously is in the 7th house, also assisting him with making deep connections. Also, these are his two main mutable placements, making him very adaptable socially.

So, in conclusion, Seungyoun has a lot of aggressive energy that is thankfully being channeled well into his work. Overall he seems gregarious and spirited, with a deep need for fulfillment through what he does, and the astrological placements to support it. Interestingly, a lot of the placements I mentioned doing this (Jupiter in Capricorn, Saturn in the 10H, Mars in the 1H), also point to someone who desires  authority, so it doesn’t surprise me that he found his way to being solo long before others in his field.

A random tangent fits nowhere: I despise the spelling of his name. Of all the ways 연 can be romanized, I didn't know this was my least favorite until I saw it.

[diffractor]

Large Cardinals 4: Measurable Cardinals

So, skipping over a bunch of weird large cardinals past indescribables, we arrive at the Measurable Cardinals. These... are kinda weird when you first learn about them. They’re the first time I got acrophobia (fear of heights) in the large cardinal hierarchy, and it suddenly wasn’t obvious at all that they existed. Inaccessibles are to set theory as infinity is to working with just the natural numbers, they’re pretty obvious. Mahlos weren’t that much more of a step. But Measurables have more of a combinatorial character instead of a largeness character. They aren’t just really really big (though they are really really big), the definition is more about having a level of infinity with certain special properties. Assuming you know what an ultrafilter is, you can skip this. If you don’t know what an ultrafilter is, read on. Let’s just take the natural numbers as an example. What would be an ultrafilter on the natural numbers? Well, it would be a classification of subsets of the natural numbers into “large” and “small”, subject to the rules: 1: The set of the natural numbers itself is “large”. 2: If a set is a superset of a “large” set, then it’s “large” 3: The intersection of finitely many “large” sets is “large” 4: Every subset of the natural numbers is either “large” or “small”, and if a set is “small”, then its complement is “large” (or vice-versa). It takes the axiom of choice to show that there’s an ultrafilter. A partial attempt at this, which should give some intuition, is letting finite sets be “small” and stuff that contains all but finitely many numbers “large”. This fulfills conditions 1, 2, and 3 (check why), but not 4. The problem with 4 is that, for example, we’ve got the set of even numbers and the odd numbers, and we need to arbitrarily choose one of them to be��“large” and the other to be “small”, and we need to make a bunch of choices like that, and make sure they’re all consistent with each other. But it can be done. Measurable cardinals can be characterized in terms of this. 1, 2, and 4 carry over, but we’ve got a stronger form of 4. Now, if the measurable cardinal is K, the rule for 3 is “the intersection of <K many “large” sets is “large”” Of course, the natural numbers work for this too, but we also require that K is uncountable (not the set of the natural numbers). So, it’s a cardinal with an ultrafilter on it that’s *really* hard to escape via intersecting things. This is what I meant by a more combinatorial sort of description instead of a “it’s really fricking big” description, and it’s not obvious that such a thing should exist. The special thing is that this ultrafilter lets you derive a bunch of other things. As an example: Let’s say it wasn’t an inaccessible cardinal. Math person I talked to said it couldn’t be the powerset of anything less than it (idk why, they didn’t explain that). So let’s say you could make K from unioning <K many things of size <K, instead. Well, as we noticed from our natural numbers example, things of size <K are “small” , things of size K may or may not be “large”. So, if we could make K via unioning together <K many “small” sets, because the complement of a small set is big, then we could make (empty set) via intersecting <K many “big” sets (the complement), which doesn’t fit with the really strong closure property on intersections. So, it’s gotta be inaccessible. Even further, you can show that the ultrafilter fulfills another special property called “normality” which is just obnoxiously strong. I don’t really get it, but some implications of it are that: if you’ve got a CLUB sequence (basically, a sequence of ordinals climbing up to the measurable cardinal, that also contain their limits. So, as an example, if omega, 2omega, 3omega, etc... are in your sequence then omega^2 should be as well), it’s “large” in the ultrafilter, and also everything “large” in the ultrafilter is stationary (inescapable by any clever means of diagonalization for cooking up larger and larger levels of infinity). Via some stuff I’m not going to go into since I don’t know it, you can show the inaccessibles below the measurable are a CLUB sequence, so... huh, that’s gotta be stationary. So the first measurable is at least a Mahlo cardinal. But you can keep going and figure out that the Mahlos below the first measurable make a CLUB sequence, so... it isn’t just Mahlo, it’s got a stationary set of Mahlo’s beneath it, which is really fricking big. And you can go “yo, like inaccessibles, let’s say a 1-Mahlo is a Mahlo with a stationary set of Mahlos beneath it, and so on for 2-Mahlos and 3-Mahlos and omega-Mahlos and... yo, we can go up the ordinals with it, K is K-Mahlo so let’s call that hyper-Mahlo, and keep going past that...” Yeah, the first measurable is bigger than all that, no matter how far you went or how clever you were in defining variants of Mahloness. It’s like, really really really absolutely incomprehensibly Mahlo. Ok, so it’s a cardinal with a ridiculously hard-to-escape ultrafilter, which can be used (via some additional work) to imply it’s stupidly huge, what else about it? Well, Measurable Cardinals are kinda like the dividing line between the small large cardinals which are just defined in terms of being big, and the large large cardinals, which tend to be defined in terms of elementary embeddings. A elementary embedding is like... let’s say we swapped out each set for some other set (maybe the same set, maybe different), but we did so in such a way that if a property holds for how (finitely many) things relate to each other, then after swapping the sets out, the same property holds. And the same in reverse. So, as an example, the empty set must be swapped out for the empty set, because it’s easy to check that something is the empty set, and that property must not change. So a lot of stuff on the lower levels gets left alone. An equivalent statement of a measurable cardinal is that they’re the critical point of a nontrivial elementary embedding from V into a transitive class M. No, I’m not going to show the equivalence. But... what does that mean? Well, a transitive set is one where, if a set B is in your set A, then every set that lies B had better be in A as well, and all the way down the line. Transitive class is the same, but, y’know, we can take a chunk out of the whole universe of sets, instead of just working in a set. So, there’s a nontrivial elementary embedding from (true universe of sets) to (fragment of universe of sets but it’s still pretty big). Nontrivial embedding just means the embedding isn’t identity, you can’t just leave everything alone. So... you swap out some stuff from (true universe of sets) for stuff from (fragment of universe of sets), but you do it in such a way that there’s really no good way to tell that anything changed (any property holding true of (x1, x2, x3...) also holds true of (j(x1), j(x2), j(x3)...) and vice-versa). This is a bit of work, but you can show that ordinals get mapped to ordinals, and ordinals can’t go down, they can’t get smaller. So ordinals either stay the same or get bigger. The critical point of an embedding is just “whats the smallest thing that shifts up and gets bigger when you do the embedding”. So, a measurable cardinal is: A thingy that moves up when you do a nontrivial embedding from the universe of sets into a fragment of the universe of sets. That means it wasn’t pinned down very well by any description (otherwise it couldn’t move). (the description as “first measurable cardinal” doesn’t quite work for technical reasons, I’m being imprecise here). So it’s really indescribable too, in a sense. Actually, you can show that measurables fulfill almost all of the smaller large cardinal axioms at the same time. A nifty feature of measurables is that they’re the first spot in the large cardinal hierarchy where they’re inconsistent with V=L. V=L was a proposed axiom of set theory by Kurt Godel, that’s basically like “yo, powersets have a bunch of undefinable sets in them, instead we’ll just take the parts of the powerset we can actually define, call that the powerset instead, and here’s how to build up the universe of sets in a pretty hierarchy”. This makes a VERY NICE model of set theory, very easy to analyze, and it settles all the stuff that’s normally unprovable one way or the other. Continuum hypothesis holds, a bunch of other stuff holds, and in general, if there’s some annoying thing in set theory you can’t prove one way or the other, you can probably prove it one way or the other in V=L. V=L can even accommodate large cardinals, but once you get to measurable cardinals... they disprove V=L, because they can show the existence of a set of numbers that’s like “here’s a list of all the ways you suck and completely fail to capture the true universe of sets, you even think some countable sets are uncountable, lmao”. So, measurable cardinals break hopes of the set-theoretic universe being easy to analyze and settling a bunch of unprovable things. Or at least, the most obvious way to do that. More on this when we get to supercompact cardinals. Now... why do we think measurable cardinals are a thing? Well, they mesh with the rest of set theory very nicely, they imply a bunch of large cardinals we’re already ok with, attempting to study them led to developing a bunch of other tools that were really useful in set theory for other reasons, we have an inner model for them (a really fine-grained view of what the set theoretic universe looks like if you chop off at the level of a measurable cardinal, like a generalization of V=L that’s fancier but is still just as nice for settling independent problems, and if they’re inconsistent, the inconsistency probably would have been flushed out when making the inner model, we’ve got a very good understanding of them). Also, they let you extend some results on sets of numbers like “is this set Lebesgue measurable” and “if we interpret this set as an infinite game between two players, does player 1 have a winning strategy” and “does the continuum hypothesis hold for sets like these”. As an example, you can show in ZFC that if there’s levels of infinity between the natural numbers and the continuum, that set isn’t going to be a closed set. Measurables let you get stronger versions of all of these. They can show that much fancier sets are Lebesgue measurable, they can show that much fancier sets/infinite games have winning strategies, and they can show that much fancier sets are also ruled out from being “thing that shows continuum hypothesis is false”.