#class 10 polynomials
Explore tagged Tumblr posts
Note
I'm Singaporean, I just saw the posts about schools in Canada vs Korea and now I'm kinda curious how things vary within this half of Asia.
Looking at your questions for the Korean asker, dyeing your hair isn't allowed but how strict the teachers will be about it probably depends on school. My secondary school (age 13-16) had one teacher who made a classmate with (presumably naturally) lighter brown hair dye it black, which was hilarious. If necessary for explanation, it was a Christian school with pretty strict rules on grooming no one had the energy to follow leading up to graduation.
We have uniforms up until you finish secondary school, then it depends on where you go. You have to buy them yourself unless you're on financial assistance or getting some kind of government subsidy, in which case I'm not sure how it works exactly.
And now the actual asking part of this ask: do y'all split math up into different subjects and if so, why??
Kids had to dye their hair to match as a group? What the fuck???? What the hell does hair matter???? Then again... bra straps and shorts don't matter either, and those are restricted everywhere, so maybe school is just dumb everywhere.
And math!!! Not super sure what you mean, but until about grade 10 here in BC all math is taught in one math class that's just "math". In grade 10 you can take precalculus or... the other one? And the idea is that Precalculus is for students going into university and the other one was for students going into trades. You NEEDED precalculus to go on to higher learning, is what we were told.
"Math" was just all math. Multiplication, geometry, algebra, etc.
"Precalculus" was all the basic skills meant to prep for calculus used in STEM stuff- polynomials, trigonometry, more algebra, that junk.
I failed it hard two times but passed the government exam so they weren't allowed to fail me again.
Also I'm good at math so they can kiss my ass now 👍
173 notes
·
View notes
Text
CMPT 419/726: Assignment 2
Assignment 2: Classification 1 Linear Models for Classification (10 marks) Provide a set of 3 linear functions y1(x), y2(x), y3(x) that would produce the decision regions shown in the figure below. x1 x2 x2 = 1 x2 = 1 x1 = 1 I.e. the decision region for class 3 contains all points with x1 + x2 > 1. 2 Kernels (20 marks) 1. Polynomial kernels (10 marks). In lecture we looked at k(x, z) = (1 + x T…
0 notes
Text
Unlocking Numerical Brilliance: How Vedic Maths Classes in Raipur Empower Students for Lifelong Success

In a world increasingly reliant on quick thinking and sharp problem-solving abilities, mental mathematics is no longer just a competitive edge—it’s a necessity. Among the most effective and time-tested approaches to mastering mental arithmetic is Vedic Maths, a system derived from ancient Indian scriptures that provides students with powerful techniques to solve complex problems quickly and accurately. Today, Vedic Maths Classes in Raipur are revolutionizing how students perceive and tackle mathematics, from early school levels to competitive examinations.
This blog dives deep into the power of Vedic Mathematics, its scientific relevance in modern education, and how it’s creating a generation of numerically confident learners in Raipur.
What is Vedic Mathematics?
Vedic Mathematics is a system of mental calculation techniques rooted in the Atharvaveda, one of the four Vedas. Rediscovered and developed in the early 20th century by Swami Bharati Krishna Tirthaji, Vedic Maths comprises 16 sutras (aphorisms) and 13 sub-sutras, which together form a cohesive framework for rapid calculations.
Unlike conventional methods that often rely on memorizing steps, Vedic Maths focuses on understanding patterns and applying logical shortcuts. This approach significantly reduces the time required to solve problems in arithmetic, algebra, geometry, calculus, and beyond.
Why Vedic Maths is Relevant Today
1. Speed and Accuracy
With Vedic methods, students can often solve mathematical problems 10 to 15 times faster than with conventional techniques—an invaluable asset in exams and competitive environments.
2. Enhanced Cognitive Skills
The focus on mental visualization, logical thinking, and systematic problem-solving enhances memory retention, focus, and overall brain function.
3. Reduction in Math Anxiety
Students who struggle with conventional math often develop a fear of numbers. Vedic Maths replaces this anxiety with curiosity and confidence, making math engaging and fun.
4. Improved Academic Performance
Mastery of Vedic Maths translates into better grades not only in math but also in physics, chemistry, and computer science, thanks to its impact on logical reasoning and numerical aptitude.
Who Should Join Vedic Maths Classes in Raipur?
Students aged 9 to 17: Ideal for middle and high schoolers preparing for board exams, NTSE, Olympiads, and entrance exams like JEE and NEET.
College students: Engineering and science students benefit from Vedic Maths in solving complex calculations without calculators.
Competitive exam aspirants: Essential for those appearing in SSC, Banking, UPSC, and Railways exams where speed and accuracy are crucial.
Educators and Tutors: Teachers enhance their teaching methodologies and help students grasp tough mathematical concepts more easily.
Curriculum Overview: What You Learn in Vedic Maths Classes
A structured Vedic Maths course is typically divided into beginner, intermediate, and advanced levels. Here’s what students learn:LevelTopics CoveredBeginnerBasic multiplication, subtraction, addition tricksIntermediateAlgebraic identities, squares, cubes, and divisionAdvancedCalculus, trigonometry tricks, polynomial functions
Each level focuses on building speed, logical fluency, and confidence in applying mental math to real-world and academic problems.
How Vedic Maths Enhances Career-Oriented Learning
In today’s dynamic educational and career environment, cross-disciplinary skills are becoming vital. For example, students pursuing Computer Hardware Repairing and Networking in Raipur often face math-heavy tasks like binary and hexadecimal conversion, power calculations, bandwidth optimization, and voltage measurement.
Here’s how Vedic Maths complements such technical disciplines:
● Binary and Decimal Conversion
Vedic methods simplify base conversions by teaching logical shortcuts and pattern recognition—skills vital in digital systems and networking.
● Problem-Solving in Electronics
Electrical calculations (Ohm’s Law, current, resistance) require quick mental math, which is significantly boosted by Vedic techniques.
● Improved Logic in Networking
Network troubleshooting often depends on logical reasoning. Vedic Maths nurtures systematic thinking, enabling better diagnostic skills and decision-making.
By combining Vedic Maths with Computer Hardware Repairing and Networking in Raipur, students become better prepared for tech-oriented roles that demand both precision and analytical capability.
Real-World Applications of Vedic Maths
Vedic Maths is not limited to exams—it has practical applications across various professions and scenarios:
Banking and Finance: Quick interest rate calculations, EMIs, and financial projections.
Entrepreneurship: Budgeting, profit-loss evaluations, and inventory management.
Data Analysis: Understanding trends, percentages, and statistical data faster.
Engineering: Structural design, material calculations, and error reduction in programming.
In short, anyone working with numbers—whether in business, education, or technology—can benefit from this ancient yet highly relevant mathematical system.
Why Choose Vedic Maths Classes in Raipur?
Raipur has seen a growing demand for Vedic Maths due to increasing academic and competitive pressures. Here’s why students and parents are choosing specialized institutes in the city:
✅ Certified Trainers
Well-trained Vedic Maths instructors with expertise in both traditional techniques and modern pedagogy ensure deep understanding and long-term retention.
✅ Structured Curriculum
Classes follow internationally recognized frameworks with clearly defined learning outcomes at each level.
✅ Individual Attention
Smaller batch sizes and periodic assessments allow personalized guidance and steady progress tracking.
✅ Integration with Other Skill Programs
Leading institutes offer blended courses that combine Vedic Maths with spoken English, computer literacy, or Computer Hardware Repairing and Networking in Raipur, preparing students for multi-dimensional career growth.
Testimonials from Raipur Students and Parents
🔸 “My daughter used to take 3 minutes to solve simple math problems. After 3 months of Vedic Maths training, she solves them in under 30 seconds. It’s amazing!” — Mrs. Anuradha Joshi, Parent
🔸 “Vedic Maths helped me crack the SSC CGL prelims with ease. I finished the quant section with time to spare!” — Ravi Dubey, Govt. Exam Aspirant
🔸 “As an engineering student learning networking, I find Vedic Maths extremely useful for doing calculations quickly without relying on calculators.” — Aman Verma, B.Tech Student
The Science Behind Vedic Maths
Recent neuroscience studies support the effectiveness of mental math techniques like Vedic Maths. Mental calculation stimulates multiple areas of the brain, including:
Prefrontal Cortex – decision-making, logic
Parietal Lobes – numerical processing
Occipital Lobes – visual imagery and memory
The use of visualization techniques in Vedic Maths activates both left and right hemispheres, ensuring holistic brain development—a stark contrast to the left-brain dominance promoted by rote learning.
How to Get Started with Vedic Maths Classes in Raipur
Getting started is simple and rewarding. Follow these steps:
Research reputed institutes offering certified Vedic Maths courses in Raipur.
Schedule a free trial class to experience the teaching style and curriculum.
Assess your child’s level through diagnostic tests provided by the institute.
Enroll in a beginner batch and track progress via weekly reports and feedback.
Consider skill bundles (like combining with computer courses or hardware networking) for holistic development.
Final Thoughts: Build the Foundation for a Numerically Confident Future
Mathematics is not just a subject—it’s a skill that defines how we think, analyze, and solve problems in everyday life. With Vedic Maths, students of all ages gain a lifelong advantage in logical reasoning, academic achievement, and career growth.
In Raipur, the growing availability of structured Vedic Maths Classes in Raipur combined with programs like Computer Hardware Repairing and Networking in Raipur offers a golden opportunity for students to sharpen their intellect and secure their future.
Investing in Vedic Maths today is an investment in cognitive power, academic excellence, and professional success tomorrow.
#tally prime gst courses in raipur#abacus classes in raipur#spoken english classes in raipur#vedic maths classes in raipur
0 notes
Text
Mastering Polynomials in Class 10: A Student’s Guide to Success
Polynomials play a crucial role in CBSE Class 10 Mathematics, forming the foundation for algebraic concepts. This guide simplifies key topics like factorization, zeros of polynomials, and quadratic equations. With step-by-step explanations, practice problems, and expert tips, students can strengthen their understanding and boost their exam performance.
To learn more, visit :
0 notes
Text
Mim Continua Ter Problems
To address the challenges outlined in the spectral approach to the Riemann Hypothesis (RH), the following research problems can be developed. These questions aim to refine the methodology, extend computational capabilities, deepen theoretical connections, and validate results rigorously:
1. Refinement of the Potential Function
Problem 1: Can physics-informed neural networks (PINNs) or other machine learning frameworks discover a potential ( V(x) ) that optimally aligns the operator’s eigenvalues with zeta zeros, while respecting physical constraints (e.g., self-adjointness, boundary conditions)?
Sub-problems:
How does the choice of neural network architecture (e.g., Fourier neural operators) affect the accuracy of the learned potential?
Can symbolic regression techniques identify an analytic form for ( V(x) ) from numerically optimized solutions?
Problem 2: Are there functional constraints (e.g., integrability, smoothness) that guarantee uniqueness of the potential ( V(x) ) for a given eigenvalue spectrum?
Investigate whether imposing symmetries (e.g., PT-symmetry) or asymptotic conditions resolves non-uniqueness.
2. Extending Spectral Computations to Higher Zeros
Problem 3: How can high-performance computing (e.g., GPU-accelerated Lanczos algorithms, distributed eigensolvers) be leveraged to compute eigenvalues of ( H ) corresponding to the ( 10^3 )-th to ( 10^6 )-th zeta zeros?
Sub-problems:
Develop adaptive discretization schemes to maintain numerical stability for large ( \text{Im}(s) ).
Optimize sparse matrix storage/operations for Schrödinger-type operators.
Problem 4: Does the spectral gap or density of ( H ) exhibit phase transitions at critical scales, and do these relate to number-theoretic properties (e.g., prime gaps)?
3. Advanced Statistical Validation
Problem 5: Can spectral form factors or ( n )-level correlation functions provide stronger evidence for the GUE hypothesis than spacing distributions alone?
Compare long-range eigenvalue correlations of ( H ) with those of random matrices and zeta zeros.
Problem 6: Do the eigenvectors of ( H ) encode arithmetic information (e.g., correlations with prime-counting functions)?
Analyze eigenvector localization/delocalization properties and their relationship to zeros.
4. Theoretical Connections
Problem 7: Can the operator ( H ) be interpreted as a quantization of a classical dynamical system (e.g., geodesic flow on a manifold), and does this link explain the spectral-zeta zero correspondence?
Explore connections to quantum chaos and the Gutzwiller trace formula.
Problem 8: Does the Riemann-von Mangoldt formula for the number of zeta zeros up to height ( T ) emerge naturally from the spectral asymptotics of ( H )?
5. Generalization to Other L-functions
Problem 9: Can the framework be adapted to study zeros of Dirichlet L-functions or automorphic L-functions by modifying ( V(x) )?
Investigate whether symmetry properties of ( H ) (e.g., modular invariance) align with functional equations of L-functions.
Problem 10: Do families of L-functions correspond to universal classes of operators (e.g., varying potential parameters), and does this align with Katz-Sarnak universality?
6. Computational and Algorithmic Improvements
Problem 11: Can hybrid quantum-classical algorithms (e.g., variational quantum eigensolvers) efficiently diagonalize ( H ) for large-scale eigenvalue problems?
Assess the feasibility of quantum advantage in spectral RH research.
Problem 12: Do multiscale basis functions (e.g., wavelets) improve the accuracy of ( V(x) ) representations compared to fixed polynomial bases?
7. Toward a Formal Proof
Problem 13: If eigenvalues of ( H ) converge to zeta zeros as discretization is refined, can this imply a rigorous spectral realization of RH?
Establish error bounds for eigenvalue approximations under discretization and optimization.
Problem 14: Can spectral deformation techniques (e.g., inverse scattering transform) reconstruct ( V(x) ) directly from the zeta zero sequence?
8. Interdisciplinary Applications
Problem 15: Does the operator ( H ) have physical interpretations (e.g., as a Hamiltonian in condensed matter systems) that could provide experimental validation?
Explore connections to quantum wires, Anderson localization, or graphene.
Summary
These problems span computational, theoretical, and statistical domains. Progress on any front would advance the spectral approach to RH by:
Strengthening the numerical evidence for a self-adjoint operator realization.
Bridging gaps between analytic number theory and quantum mechanics.
Developing tools applicable to broader problems in mathematical physics and L-function theory.
Collaboration across disciplines (e.g., machine learning, quantum computing, analytic number theory) will be critical to addressing these challenges.
0 notes
Text
NCERT Books for Class 9: A Comprehensive Guide to Building a Strong Academic Foundation
Class 9 is a crucial stage in a student’s academic journey, as it lays the foundation for higher classes and introduces more complex concepts across all subjects. The National Council of Educational Research and Training (NCERT) books are widely recognized as the primary study material for students in India, especially those enrolled in schools affiliated with the Central Board of Secondary Education (CBSE). These books are meticulously designed to provide in-depth knowledge while ensuring clarity and accessibility for students of varying abilities. This article delves into the significance of NCERT books for Class 9, their unique features, and how they contribute to academic success.

Why Are NCERT Books Important for Class 9?
NCERT books are considered the gold standard for academic study in Indian schools, and this is particularly true for Class 9. Here's why they hold such importance:
Conceptual Clarity: NCERT books emphasize a strong understanding of fundamental concepts. Rather than overloading students with unnecessary details, the content is streamlined to focus on essential ideas. This clarity is crucial in Class 9, as students encounter new topics that form the base for Class 10 and beyond.
Aligned with CBSE Curriculum: These books strictly adhere to the CBSE syllabus, ensuring that students study only what is required for their examinations. This alignment also makes NCERT books the most reliable source for CBSE board exams.
Wide Acceptance in Competitive Exams: NCERT books are highly recommended for competitive exams like JEE, NEET, and UPSC. Class 9 concepts, especially in subjects like Mathematics and Science, form a significant portion of the syllabus for these exams.
Cost-Effective and Accessible: NCERT books are affordable and widely available in print and digital formats. The NCERT’s initiative to provide free e-books on their official website has further improved access to quality education materials.
Features of NCERT Books for Class 9
Structured Presentation: The chapters in NCERT books are well-organized and presented systematically. Each chapter begins with an introduction to the topic, followed by examples, illustrations, and exercises that reinforce the concepts discussed.
Language Simplicity: The language used in NCERT books is straightforward and easy to understand. This ensures that students grasp complex concepts without feeling overwhelmed.
Inclusion of Practical Knowledge: NCERT books often provide real-life examples and applications of theoretical concepts. For instance, Science books include experiments and activities to make learning more engaging and interactive.
Illustrations and Diagrams: Visual aids like diagrams, charts, and tables are extensively used to simplify complex topics, especially in subjects like Science and Geography.
End-of-Chapter Exercises: NCERT books include a variety of questions at the end of each chapter, ranging from objective-type to descriptive questions. These exercises are crucial for exam preparation and help students test their understanding of the topics.
Subject-Wise Overview of NCERT Books for Class 9
1. Mathematics
The NCERT Mathematics book for Class 9 introduces concepts like Polynomials, Coordinate Geometry, and Linear Equations. It emphasizes problem-solving skills and logical reasoning, preparing students for advanced topics in higher classes. Each chapter includes solved examples, practice questions, and summaries for better comprehension.
2. Science
The Science textbook is divided into three sections: Physics, Chemistry, and Biology. Topics such as Motion, Atoms and Molecules, and Diversity in the Living World are presented in a simple yet engaging manner. Practical experiments and activities are included to enhance conceptual understanding.
3. Social Science
Social Science comprises History, Geography, Political Science, and Economics. The books provide a detailed exploration of topics like the French Revolution, Natural Vegetation, Electoral Politics, and Poverty as a Challenge. The use of case studies and maps makes these subjects more relatable and interesting.
4. English
The NCERT English books for Class 9, including "Beehive" and "Moments," focus on language development, comprehension, and creative writing skills. Through prose, poetry, and supplementary stories, these books encourage students to appreciate literature while improving their communication abilities.
5. Hindi and Sanskrit
For language subjects like Hindi and Sanskrit, NCERT books introduce students to grammar, vocabulary, and literary works. These books aim to strengthen linguistic skills while fostering an appreciation for India’s rich literary heritage.
Conclusion
NCERT books for Class 9 are invaluable resources that provide a solid foundation for academic success. Their focus on conceptual clarity, simplicity, and relevance ensures that students are well-prepared for both school exams and competitive exams. By thoroughly studying NCERT books and utilizing their exercises effectively, Class 9 students can achieve a deeper understanding of their subjects and build confidence for future challenges. Embracing these books as a primary study resource is a step toward academic excellence and holistic learning. Originally Published: Blogspot.com
#khansir#upscstudymaterials#book for ncert#book ncert download#ncert book for upsc#studying#books#ncert book for class 9#ncert book for class 9 maths
0 notes
Text
https://youtu.be/NfLA0FVN2Ok?si=Y1xQ4n_MoClF4vi8
#learnatscholar#scholarclassesvadodara#class10math#cbse#ncert#classesinwarasiya#bestclassesinwarasiya
0 notes
Text
How to Sign Up for the Maths Olympiad - Enrolling Made Easy
The Indian National Mathematical Olympiad (INMO) is a top-notch math competition for high schoolers in India, running since 1989. Hosted by the Homi Bhabha Centre for Science Education, it's a big deal for students after the tenth grade. Starting with the Regional Mathematical Olympiad (RMO) and leading up to the International Mathematical Olympiad (IMO), each stage gets students one step closer to global fame. Ready to flex those brain muscles of your child?
Steps of the Maths Olympiad
Want to ace the Maths Olympiad? Here's the scoop:
Process 1: IOQM (Indian Olympiad Qualifier in Mathematics)
Kick-off with a 3-hour quiz featuring 30 multiple-choice questions. Just fill in your answers on an OMR sheet—easy, right?
Process 2: INMO (Indian National Mathematics Olympiad)
This stage features six challenging questions over a four-hour period. Solutions must be written on a response script and submitted with rough sheets at the end of the test.
Process 3: OCSC (Orientation Cum Selection Camp)
Top performers from the INMO, approximately 35 students, are invited to the International Mathematical Olympiad Training Camp (IMOTC). This camp prepares students for the IMO.
Process 4: PDT (Pre-Departure Training Camp)
Six top-performing students from IMOTC receive intense training for 8-10 days. Top-notch gurus from all corners of the country whip these students into shape for the IMO showdown.
Step 5: The Big Math Showdown (International Mathematics Olympiad)
In this last stage, teams from more than 100 countries face off. Each team has up to six brainy students, plus their leaders and mentors.
Eligibility
To take the INMO exam, students need to ace the first level. Simple as that!
Typically, around 30 students from classes 8 through 12, including five female candidates fulfilling the girls’ quota, are shortlisted. Special provisions exist for students from KV schools outside India who can bypass the selection process, although 12th-grade girls in KVs are not eligible for the girls' quota.
Syllabus
The INMO syllabus includes advanced topics such as:
Arithmetic of Integers
Geometry
Quadratic Equations & Expressions
Trigonometry
Coordinate Geometry
Systems of Linear Equations
Permutations & Combinations
Inequalities
Elementary Combinatorics
Probability Theory
Number Theory
Finite Series & Complex Numbers
Elementary Graph Theory
Polynomial Factorization
How to Enroll in the Maths Olympiad
Through Schools
Students can access the IMO Registration Form via their schools. Registered schools receive a prospectus and registration paperwork. Schools not registered can request a prospectus via the SOF website.
Through Mentorship Programs
Enrolling through a mentorship program like Sri Chaitanya’s Early Champions Advantage can provide significant benefits. Their carefully crafted curriculum, built on years of research, tackles the unique hurdles students face in Olympiads like a pro.
Conclusion
Joining the Maths Olympiad isn’t just about winning trophies; it’s about getting really good at math and solving tricky problems. Taking that first step can be scary, but with the right help, students can shine. Need a boost? Check out programs that give students a leg up in every part of the Maths Olympiad journey. Start your journey today and take your mathematical skills to new heights!
0 notes
Text
Benefits of Learning: Digital Classes for 9th & 10th Math and Science

We all know that 9th and 10th class math and science could be difficult. It is generally the first important year of examinations for students, which can be difficult. Parents frequently believe that taking their children to extra classes would help them perform better. While this may be true, it might be difficult for students.
That’s the reason why online courses come in useful. They work similarly to smart classrooms, allowing students to view and engage with the material they are studying. Instead of simply remembering information, people may observe how things function. Learning becomes as simple as installing an app!

Now, students in 9th and 10th grade do not have worries about their classes. Using digital class apps allows them to follow along with their math and science classes. It helps them understand every detail and increases their problem-solving abilities.
Students can also access lessons from other educational platforms when taking classes digitally. Therefore, you are free to explore different syllabi while you are studying the current one. These days, learning is more about truly understanding things than taking exams.
Also, look at the most recent 9th and 10th class syllabuses, which may be helpful!
Class 9 Math's: Unit-wise
Unit 1-Real numbers
Unit 2-Polynomials and Factorization
Unit 3-The Elements of Geometry
Unit 4-Lines and Angles
Unit 5-Co-Ordinate Geometry
Unit 6-Linear Equations in Two Variables
Unit 7-Triangles
Unit 8-Quadrilaterals
Unit 9-Statistics
Unit 10-Surface Areas and Volumes
Unit 11-Areas
Unit 12-Circles
Unit 13-Geometrical Constructions
Unit 14-Probability
Unit 15-Proofs in Mathematics
Class 9 Physics Syllabus: Chapter-wise
Chapter 1-Matter Around Us
Chapter 2-Motion
Chapter 3-Laws of Motion
Chapter 4-Refraction of Light at Plane Surfaces
Chapter 5-Gravitation
Chapter 6-Is Matter Pure?
Chapter 7-Atoms and Molecules
Chapter 8-Floating Bodies
Chapter 9-What is inside the Atom?
Chapter 10-Work and Energy
Chapter 11-Heat
Chapter 12-Sound
Class 9 Biology Syllabus: Chapter-wise
Chapter 1-Cell its structure and functions
Chapter 2-Plant tissues
Chapter 3-Animal tissues
Chapter 4-Plasma membrane
Chapter 5-Diversity in Living Organism
Chapter 6-Sense Organs – I
Chapter 7-Sense Organs – II
Chapter 8-Animal behavior
Chapter 9-Challenges in Improving Agricultural Products
Chapter 10-Adaptations in Different Ecosystems
Chapter 11-Soil pollution
Chapter 12-Bio geochemical cycles
The Telangana State Board (TS) students who are looking for the Class 9 Physics, Biology Syllabus can find it in the syllabus mentioned above. moreover, review the AP Class 9th syllabus also.
Class 10 Math and Science Syllabus:
The Telangana State Board Class 10 math's syllabus is given below; class tenth With the use of this TS 10th Class Math's Textbooks Syllabus, students may prepare for their final exams and have an effective understanding of the subject matter, therefore achieving the highest marks possible.
10th Class Math's: Unit Wise
Unit 1-Real numbers
Unit 2-Sets
Unit 3-Polynomials
Unit 4-Pair of Linear Equations in Two Variables
Unit 5-Quadratic Equations
Unit 6-Progressions
Unit 7-Coordinate Geometry
Unit 8-Similar Triangles
Unit 9-Tangents and Secants to a Circle
Unit 10-Mensuration
Unit 11-Trigonometry
Unit 12-Applications of Trigonometry
Unit 13-Probability
Unit 14-Statistics
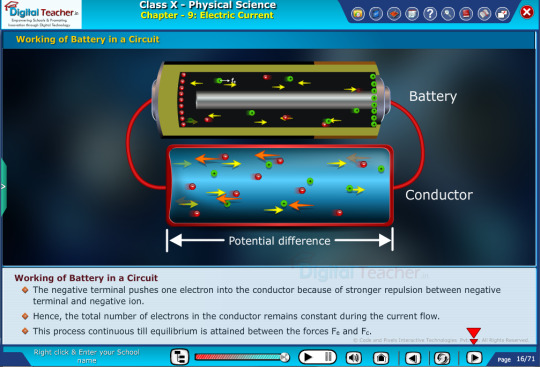
Class 10 Physics Syllabus: Chapter Wise
Chapter 1-Reflection of Light by Different Surfaces
Chapter 2-Chemical Reactions and Equations
Chapter 3-Acids, Bases and Salts
Chapter 4-Refraction of Light at Curved Surfaces
Chapter 5-Human Eye and Colorful World
Chapter 6-Structure of Atom
Chapter 7-Classification of Elements – Periodic Table
Chapter 8-Chemical Bonding
Chapter 9-Electric Current
Chapter 10-Electromagnetism
Chapter 11-Principles of Metallurgy
Chapter 12-Carbon and Compounds
10th Class Biology Syllabus: Chapter-Wise
Chapter 1-Nutrition
Chapter 2-Respiration
Chapter 3-Transportation
Chapter 4-Excretion
Chapter 5-Coordination
Chapter 6-Reproduction
Chapter 7-Coordination in Life Processes
Chapter 8-Heredity
Chapter 9-Our Environment
Chapter 10-Natural Resources
The TS Board Class 10 Math's & Science topic syllabus is available above, complete with chapter-by-chapter details. Students can go through the most recent math and science syllabus to be aware of all the key subjects they need to study for exams.
Additionally, visit the below pages. We hope you found these pages useful:
Telangana Board Syllabus Related Links
Telangana Board Class 6 Syllabus
Telangana Board Class 7 Syllabus
Telangana Board Class 8 Syllabus
Telangana Board Class 9 Syllabus
#elearning#digital class#digital classes online#digital classroom#digital content#digital learning#digital teacher#smart class#online learning
1 note
·
View note
Text
Is learning only formulas of QUADRATIC EQUATIONS enough?
Remember solving the questions from polynomials? No? Here’s an example so that you can understand Quadratic equations.
2x2+3x+1

Still not sure about the concepts from polynomials? Take a test of polynomials in class 9 on the SeekoG app so that you can save time by understanding Quadratic equations better and faster.
Now that you are confident about polynomials, do you know that it is very much related to Quadratic equations? But how?
Here’s how – Try Equating a quadratic expression to a constant and this is how you get a quadratic equation. For example- the above-given expression has been converted to an equation.
2x2+3x+1= 0
Other than this do you know the points that are quite important in these equations?
Let’s take px2+qx+r=0 as an example.
Here are some key points that need to be remembered by all of you:
p and q are the coefficients of x
In a quadratic equation, the value of p should not be equal to 0.
The roots of a quadratic equation are the only value of x that could satisfy the equation.
Not many points to remember. This chapter is quite easy, right? Actually, this is just a small drop from the sea of quadratic equations. You now know about roots but what about the value of roots? How will you find it? Is there some specific formula for finding these?
Well, there is a formula to find the roots of the equation. But other than the method that involves a formula, there is another method as well. So, what are these methods? Now this should be answered by you. Take the test & use the methods you know to be ready for your class 10 Maths Quadratic Equations!
It's great to know about quadratic equations but won't it be excellent to know about the Cartesian plane? Click to read more.
0 notes
Text
Establishing a Firm Mathematical Ground: NCERT Class 10 Maths Solutions
Introduction:
Mathematics is a subject that both fascinates and challenges students. It forms the basis for various scientific and technological advancements and plays a crucial role in shaping logical thinking and problem-solving skills. To build a strong foundation in mathematics, students often turn to reliable resources such as NCERT Class 10 Maths Solutions. In this blog, we will explore the significance of NCERT Class 10 Maths Solutions in establishing a firm mathematical ground for students.
Understanding the Importance of NCERT Class 10 Maths Solutions: NCERT (National Council of Educational Research and Training) is a trusted authority when it comes to creating educational resources in India. Their Class 10 Maths Solutions provide a comprehensive and structured approach to learning mathematics. These solutions are designed to help students grasp fundamental concepts, develop critical thinking skills, and prepare effectively for examinations.
Comprehensive Coverage of the Syllabus: NCERT Class 10 Maths Solutions cover the entire syllabus prescribed by the Central Board of Secondary Education (CBSE). Each chapter is explained in a step-by-step manner, offering a thorough understanding of concepts and their applications. From real numbers and polynomials to trigonometry and statistics, these solutions leave no stone unturned in ensuring students have a strong grasp of every topic.
Clear and Detailed Explanations: One of the standout features of NCERT Class 10 Maths Solutions is their clear and detailed explanations. Complex concepts are broken down into simpler terms, making it easier for students to follow along. The solutions provide ample examples and illustrations, helping students visualize mathematical problems and their solutions. The step-by-step approach ensures that students can grasp the logic behind each solution, thereby building a deeper understanding of the subject.
Practice Makes Perfect: NCERT Class 10 Maths Solutions also include a wide range of practice exercises and additional problems for students to solve. These exercises are carefully crafted to reinforce concepts and improve problem-solving skills. By regularly practicing these problems, students gain confidence in their abilities and develop a solid foundation in mathematics.
Exam Preparation Made Easy: With board examinations and competitive entrance tests on the horizon, NCERT Class 10 Maths Solutions prove to be invaluable study material. The solutions are aligned with the examination pattern and provide ample practice through sample papers and previous years' question papers. By regularly solving these papers with the help of NCERT solutions, students become familiar with the exam format and are better prepared to tackle challenging questions.
Conclusion:
NCERT Class 10 Maths Solutions act as a guiding light for students on their mathematical journey. By using these solutions, students can establish a firm foundation in mathematics, develop problem-solving skills, and excel in examinations. The comprehensive coverage, clear explanations, and ample practice opportunities make NCERT Class 10 Maths Solutions an indispensable resource for students aiming to succeed in the field of mathematics. So, let's embrace these solutions and pave the way for a strong mathematical future!
0 notes
Text
A society of triangles would be more classist than any human society.
You're a triangle in this society. You're extremely lucky, because one of your sides is an algebraic number. It is a root of 18224x^11+52304x^10-220983x^9-400981x^8-187265x^7+7228x^6+7011829x^5+65564x^4-19022x^3+5102x^2-43098x+177. You treasure that polynomial deeply. At just 12 coefficients, it's remarkably short, which provides you with an incredible amount of prestige within triangles with one algebraic side. It was once considered by a computer, for a millionth of a second, as part of some brute-force search. Your specific root was never considered, but it's still more than most of your peers. Your two transcendental sides have, of course, never come close to being noticed.
Within society as large, a very few specific triangles reign. 1-1-1 is the most important, naturally, but 3-4-5 is always trying to make a power play. Those two have more power than the infinite other equilateral triangles with integer side lengths and Pythagorean triangles below them combined. Beneath those is the rational side length equilaterals, the rational right angles, and so on, each with their own internal hierarchies as well. All of the countably infinite groups are exhausted before you reach the uncountably infinite algebraic equilaterals. Somewhere many tiers down is you. You're still quite fortunate though. Essentially all triangles are a tier below you, the triangles with three different transcendental side lengths and no other redeeming features. That group has its own structure as well, using computability and the like, but it doesn't bother you much. The scraps they compete for are literally nothing compared to your own prestige, which is literally nothing compared to that of a couple tiers above you, and so on to the top.
There is essentially no social mobility. Being glimpsed by a human is the only way to truly move classes beyond the conditions of your existence. There are a few who have managed. The triangle with sides e, π, and e^π, for example, sits many ranks above what its sides would suggest. But even then, those numbers aren't considered important for triangles by humans, so it sits well below where you might expect. For most triangles in the bottom tier, just a single side length of a notable transcendental provides no real value.
There's no positive end to this story.
It's gross being made of meat but unlike some of you I understand that it would be equally gross being made of metal. the only non gross form of being is pure abstraction.
2K notes
·
View notes
Text
Class 10 Maths NCERT Solutions Chapter 2 Polynomials
Class 10 Maths NCERT Solutions Chapter 2 Polynomials

Polynomials Class 10 Maths NCERT Solutions
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 2 Polynomials.
Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.1
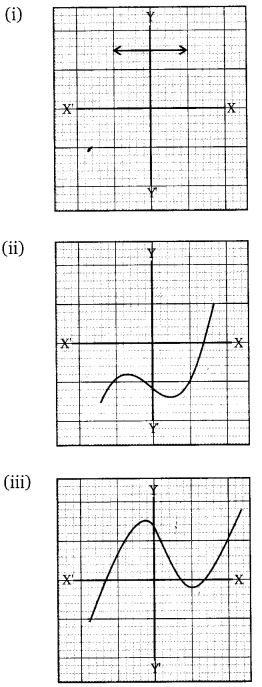
Question 1: The graphs of y = p(x) are given below for some polynomials p(x). Find the number of zeroes of p(x) in each…
View On WordPress
#ch 2 maths class 10#chapter 2 maths class 10#class 10 ch 2 maths#class 10 maths chapter 2#Class 10 Maths NCERT Solutions Chapter 2 Polynomials#class 10 maths polynomials#class 10 polynomials#NCERT Solutions For Class 10 Maths Chapter 2#polynomial class 10#polynomials class 10#polynomials class 10 ncert solutions
2 notes
·
View notes
Text
Class 10 Maths NCERT Solutions Chapter 2 Polynomials
Class 10 Maths NCERT Solutions Chapter 2 Polynomials

Polynomials Class 10 Maths NCERT Solutions
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 2 Polynomials.
Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.1
Question 1: The graphs of y = p(x) are given below for some polynomials p(x). Find the number of zeroes of p(x) in each…
View On WordPress
#ch 2 maths class 10#chapter 2 maths class 10#class 10 ch 2 maths#class 10 maths chapter 2#Class 10 Maths NCERT Solutions Chapter 2 Polynomials#class 10 maths polynomials#class 10 polynomials#NCERT Solutions For Class 10 Maths Chapter 2#polynomial class 10#polynomials class 10#polynomials class 10 ncert solutions
2 notes
·
View notes
Text
Class 10 Maths NCERT Solutions Chapter 2 Polynomials
Class 10 Maths NCERT Solutions Chapter 2 Polynomials
Polynomials Class 10 Maths NCERT Solutions
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 2 Polynomials.
Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.1
Question 1: The graphs of y = p(x) are given below for some polynomials p(x). Find the number of zeroes of p(x) in each…
View On WordPress
#ch 2 maths class 10#chapter 2 maths class 10#class 10 ch 2 maths#class 10 maths chapter 2#Class 10 Maths NCERT Solutions Chapter 2 Polynomials#class 10 maths polynomials#class 10 polynomials#NCERT Solutions For Class 10 Maths Chapter 2#polynomial class 10#polynomials class 10#polynomials class 10 ncert solutions
0 notes
Text
Class 10 Maths NCERT Solutions Chapter 2 Polynomials
Class 10 Maths NCERT Solutions Chapter 2 Polynomials
Polynomials Class 10 Maths NCERT Solutions
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 2 Polynomials.
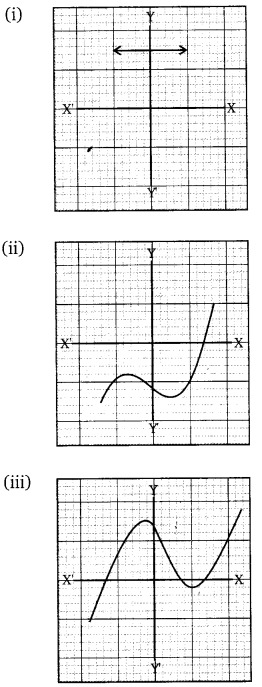
Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.1
Question 1: The graphs of y = p(x) are given below for some polynomials p(x). Find the number of zeroes of p(x) in each…
View On WordPress
#ch 2 maths class 10#chapter 2 maths class 10#class 10 ch 2 maths#class 10 maths chapter 2#Class 10 Maths NCERT Solutions Chapter 2 Polynomials#class 10 maths polynomials#class 10 polynomials#NCERT Solutions For Class 10 Maths Chapter 2#polynomial class 10#polynomials class 10#polynomials class 10 ncert solutions
0 notes