#cognisance

[positively-knotted]

Poll time, but this time linear algebra.

Arguments for any position appreciated!

[pilsbury-bland-bread]

As a mathematician, I dislike the phrase "another day that ends in y". There is a trivial stronger statement! Rejoice for today is "another day that ends in day", and there will be no follow-up questions after your seminar about sufficiency

[pilsbury-bland-bread]

their south slavic ouchie dicks Vs The Mighty Macedonian Pain-Free Penis

Mediterranean apathy metaphors

[positively-knotted]

Who let the computer scientists do humanities

[pilsbury-bland-bread]

I follow the fraxiom tag because of the musician. I have discovered they are less popular than two gay wrestlers. One's name is definitely axiom. The other I have genuinely no clue. I have to assume it's frank.

[positively-knotted]

Does anyone have recommendations for nice fun maths things to read?? Short textbook/expo paper or something of that ilk.

I've taken a bit of a maths break before starting my PhD which has been fab, but keen to get a bit back into it. Ideally something geometric (manifold topology >>) but open to anything cool. The papers my supervisor told me to read are not acceptable suggestions.

[positively-knotted]

commuting to the bit. yeah ill be the same no matter which way i go there

commuting to the bit. yeah ill be there in about 40 minutes just keep stalling

[pilsbury-bland-bread]

Is the whole "Gulf of America" thing that big of a deal? Like it's a weird show of nationalism but like, on the scale of things it seems very small? Idk different countries speaking different languages often have different names for the same bodies of land/water. And renaming is sorta weird, but feels smaller than when turkey tried insisting that we call it Türkiye.

[positively-knotted]

In tags under my response to @algebraic-dumbass, @associativeglassdesert said:

(If you've not seen that post, go read it).

This is interesting to me, but does go some way towards explaining why people like Lockhart's Lament. I've definitely seen other people express similar sentiments. However, I don't really get it.

High school geometry is terrible because it's boring. Lockhart does get that right. It's terrible for exactly the same reason that high school history and high school English and high school drama are terrible. People don't care. So you can't ask them to do anything hard, and therefore anything interesting.

Mathematicians often have this viewpoint that if only we got people to do this or that kind of maths in high school, it would be "better". Now a lot of that has merit, don't get me wrong. I think more emphasis on proof would be good for society at large. But even a more proof-heavy high school algebra would suck. It would still be boring to most people, because most people aren't mathematicians. And that's ok!

I don't know how to solve that problem, especially not at 2am, but I think the answer that "high school geometry sucks because it's insufficiently creative" or "it's too far from university geometry" are just pushing the problem elsewhere. You're just making it boring for a different subset of people. The problem is with the concept of standardised curricula much more than any individual course anyone could design.

[pilsbury-bland-bread]

Rating the Western Protestant names of Easter Related days

Palm Sunday. 6/10 Kinda cool. Immediately reminds you of waving fake palm leaves as a child in front of a very tired looking congregation. More days should be named after plants.

??? Monday and ??? Tuesday. 0/10. Do these even have names. Why not. Jesus never took a day off, neither should the calendars.

Spy Wednesday. 10/10. Hell yeah. Need I say more?

Maundy Thursday. 9/10. A complete monopoly on the word "maundy". Genuinely think that word only refers to this specific day of the year. A power play. However suspiciously similar to "Monday", and being more similar to a Monday (the second worst day of the week) is the last thing Thursday (already the worst day of the week) needs.

Good Friday. 1/10. Skull Friday was right there. Death Friday. Black Sky Friday. The only thing this achieves is getting primary school children to ask "why is it good if jesus was unalived". And then instead of being told to say merk like a mid-noughties grime artist, they get lectured about how we no longer have to kill lambs. Which noone was gonna fucking be doing anyway. Stupid day, stupid name.

Holy Saturday. 3/10. Every Saturday is holy when I'm there. Because I'm thinking about Jesus. Of course.

Easter Sunday. 4/10. Eh, they didn't really have a choice on this one, so I can't dock too many points. But still, surely there's a more creative option. Resurrection Sunday would be better I suppose, since that doesn't happen every Sunday. Although possibly more Sundays than just one, I can't remember if we know the day of the week that Lazarus was raised on.

Easter Monday. 1/10. A repeated word? Do better. We should steal Bright Monday from the Greeks. Although it has rained on every Easter Monday I remember which sucks bc it's a day off. So maybe we shouldn't jinx it any more than we already do.

[pilsbury-bland-bread]

Also when I didn't pay attention I was never on my phone: if that got caught it would get taken away. So it was still doodling and passing notes, even with phones

"kids don't pay attention in class anymore Because Of Phone" is so funny as an argument. students haven't paid attention in class since school was invented. my parents' generation were in there making flipbooks out of the corners of their notebooks and doodling random shit instead of taking notes. and they didn't have phones.

[positively-knotted]

Can you explain why four dimensions is so special? I’ve heard that, in very broad strokes, for n < 4 the ways things can “fit together” are relatively limited, while for n > 4 there’s enough space to freely move things around and cut chunks out, and somehow at n = 4 these forces of restriction and freedom balance out. But I’d love to get a more detailed description. Does it really all just come down to surgery only working for n > 4?

The broad strokes are basically right. But if you want a more detailed answer, I think we can go slightly more simple than surgery.

Suppose we have an ambient n-manfold M, and two submanifolds A, B which intersect transversely in two points, with opposite orientation. Formally, pick an arc in A and an arc in B between the two points. Assign local orientation to one point, transport this orientation along each arc. These orientations should disagree by the time we reach the other intersection point.

We would ideally like to resolve these intersections, kinda like this. This is called the Whitney trick.

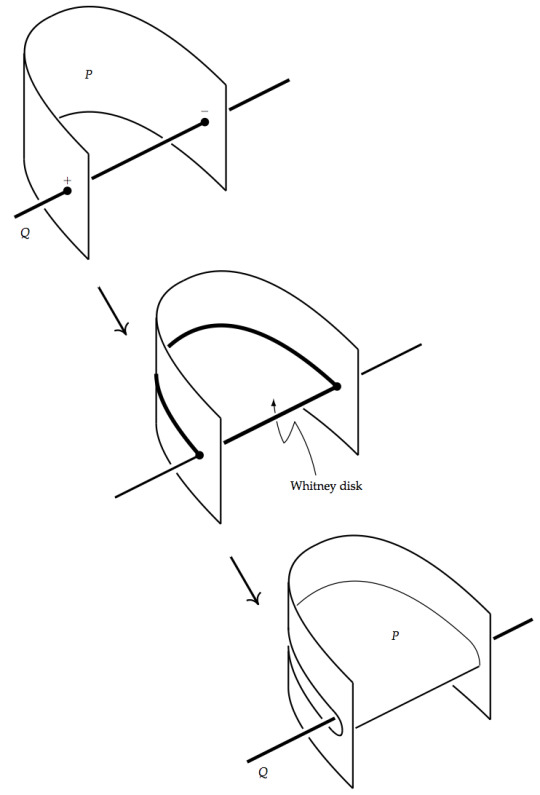
Again, more formally, what this involves is finding a disc bounded by those two arcs (whose interior is disjoint from A and B), and "pushing A off of B along the disc". Details aren't hard, but the picture is more helpful.

It turns out that (so long as the loop formed by the union of the arcs is nullhomotopic in M), this is always possible if n≥5. If n=4, it's sometimes possible, but sometimes not. But whereas it's "generally not possible" in the smooth setting, it is "generally possible" topologically.

This intersection resolving is how you prove the h-cobordism theorem, and hence high-dimensional Poincaré, etc. When trying to do surgery, Freedman showed that the arising situations are ones that work topologically but not smoothly (for a large class of fundamental groups at least). So the topological surgery sequence is exact, while the smooth one isn't.

In lower dimensions, this completely doesn't work, but in exchange DIFF and TOP are equivalent categories so it doesn't matter at all.

[pilsbury-bland-bread]

I wonder how long it would take field linguists to discover that modern (SSB) English doesn't have optional OSV word order. When I say "lovely shoes you've got" there's actually a dropped expletive subject, dropped copula, and dropped relative clause marker! But it ends up looking like object fronting!

[positively-knotted]

poll poll poll poll

Curious as to what people's opinions on this are

[pilsbury-bland-bread]

who up submitting their paper

[positively-knotted]

What's the maths canon?

There are definitely some books which are The Books on whichever topic/course they relate to. Stuff like Hatcher, (baby/...) Rudin, Fulton-Harris, Hartshorne (tho maybe Vakil has taken over there somewhat).

But what about first/second year of an undergraduate course? Dummit & Foote is probably as close as there is for basic algebra, although linear algebra? Is there a linear algebra canon? Probability?