#orthogonal diagonalizer

[destroyer-of-monsters]

GODZILLA ULTIMA

VS

JET JAGUAR

I remade some of my old GIFs of this fight, and added two new ones as well. Such a tremendous ending, i remember being shocked the moment Jet Jaguar became giant and being like NO F#CK WAY THEY ACTUALLY DID IT!

[der-unverantwortliche]

Still #SoTrue, was thinking today (because I found this in my old itunes library) also of the way ASOUE is almost self-parodically culturally jewish the same way HP is almost self-parodically culturally christian

[flaxen-phoenix]

Deicide Chess

I was fucking around on some chess variant resource pages and found this tool called the Board Painter, which allows you to create your own setups for custom chess variants. I played around with it for a bit, searched through all the piece graphics, started toying around with them... and then I made the board 16x16.

Eventually, I ended up with a board that looked like this. 16x16, with no less than 25 unique piece types.

I call it "Deicide Chess", because God is dead and I looked him square in the eye as I pulled the trigger. Full rules are under the cut.

Before I explain the piece movements, here's a short glossary of terms that I'll use when describing them.

Step - Movement to an adjacent square. Notated with a dot in the destination square, or an X for capturing-only steps.

Slide - Movement along a straight path of unoccupied squares to reach a square that is not adjacent. Notated with an arrow that follows the path of squares.

Jump - Movement directly to a square that is not adjacent, ignoring any pieces that may be in the way. Notated with an arrow.

(X, Y) jump - When a piece makes an (X, Y) jump, it jumps X squares in one orthogonal direction, then Y squares in a different, perpendicular direction. X and Y can be swapped freely, so an (X, Y) jump is equivalent to a (Y, X) jump.

Orthogonal - Forward, backward or sideways, perpendicular to the edges of the board.

Diagonal - An equal amount of movement along two perpendicular orthogonal directions.

Forward - Towards your opponent's side of the board. (Backward, similarly, is towards your own side of the board.) For White, this would be moving towards the 16th rank of the board, while for Black it would be moving towards the 1st rank.

In any direction - Orthogonally or diagonally.

(Unless otherwise stated, and with the exception of the above definitions, "move" specifically refers to non-capturing moves, while "capture" specifically refers to capturing moves. "Giving check" refers to capturing moves that can only target a King.)

The King

Moves or captures by stepping one square in any direction.

Royal - If your King is threatened with capture, you are in check, and you MUST remove the threat. If you cannot remove the threat, you are checkmated and you lose the game. You may not willingly move into check.

Castling - Castling is done by having the King move two squares towards its Rook, then the Rook jumps to the square the King passed through. The King may not castle into, out of or through check, all squares between the King and Rook must be open, and neither the King nor the Rook used may have been moved this game.

The Queen

Moves or captures by sliding any number of squares in any direction.

The Rook

Moves or captures by sliding any number of squares in an orthogonal direction.

The Bishop

Moves or captures by sliding any number of squares in a diagonal direction.

The Knight

Moves or captures by making a (2, 1) jump.

The Pawn

Moves by stepping one square straight forward. Captures by stepping one square diagonally forward.

Head Start - May slide up to four squares forward if it is on or behind its starting rank. (For white Pawns, this only works if done while on or behind the 4th rank, for black Pawns, only on or behind the 13th rank.)

En Passant - If an opposing Pawn uses its Head Start to move past a square where your Pawn could have captured it, you may move your Pawn into that square, then capture the opposing Pawn anyway.

Promotion - A Pawn that reaches the other side of the board (the 16th rank for white Pawns, or the 1st rank for black Pawns) becomes any piece except for a King, another Pawn, a Drunk Pawn, or a Rookie.

The Archbishop

Has all the movement capability of both the Bishop and the Knight.

The Chancellor

Has all the movement capability of both the Rook and the Knight.

The Cannon

Moves like a Rook, but cannot capture like one. Instead, to capture a piece, there must be a hurdle of either color between the Cannon and its target, which the Cannon jumps over to reach the target. The Cannon may not jump if not capturing, and may only jump over exactly one piece per move.

The Archer

Moves like a Bishop, but cannot capture like one. Instead, to capture a piece, there must be a hurdle of either color between the Archer and its target, which the Archer jumps over to reach the target. The Archer may not jump if not capturing, and may only jump over exactly one piece per move.

The Time Machine

Moves and captures like a Queen, but three turns into the future. To do this, declare a valid square that the Time Machine will land on, then remove it from the board with three time counters. Every turn, after you make your move, remove a time counter from the Time Machine, then if there are no time counters left, return it to the board on the square that was declared three turns ago. Any piece in that square is captured, even if it's a friendly piece. The Time Machine threatens the square it's about to land on, even if there are still some turns left before it will land. Kings who are standing in that square are in check, and if a Sumo Wrestler could push a King onto the square a Time Machine is about to land on on the next turn, that King is in check.

The Champion

Moves and captures by stepping exactly one square orthogonally, or jumping exactly two squares in any direction.

The Wizard

Moves and captures by stepping exactly one square diagonally, or making a (3, 1) jump.

The Kitsune

Moves and captures by making a doubly-bent sliding move; first, the Kitsune steps one square in an orthogonal direction, then turns 45 degrees left or right and slides any number of squares (including 0) in the resulting diagonal direction, then turns 45 degrees left or right again and steps one square in the resulting orthogonal direction. The Kitsune cannot capture until the final orthogonal step.

To be Continued... (because I ran out of space for images on this post)

[houndsofbalthazar]

There are too many flags that are similar to each other[1]. I am considering doing a series of polls to decide who gets to keep the flag and who has to change.

I am at least going to do this one poll, and I am going to start with a slightly unusual one because most of the flags in this poll are fairly distinct from each other, but they share a common element, that is to say today we're asking who gets to keep the Union Flag (aka the Union Jack[2])?

The flag of my home country isn't actually one that I hate. It's doing some interesting stuff with both an orthogonal and diagonal cross while most flags restrict themselves to one, something unique but still very flaggy. It's got that subtle rotational only symmetry so you can have a go at people who hang it upside down.

It's not bad. But it is overused. It appears in the top left of many other flags, and I think overuse has made me appreciate it less.

Here are the other contenders, their flag pictured below the name of the country: Australia

Fiji

New Zealand[3]

Tuvalu

With the contenders introduced, it's time for the big question:

Footnotes: [1] I don't actually think this. I like and enjoy it.

[2] Look, this would flow so much better and be funnier if I just asked "who gets to keep the union jack", but I was once a very pedantic child and a fact that I learnt which to be honest might not even be a fact is that it's only called the union jack when it's flown at sea, and on land it's the union flag. While I am older, possibly wiser, and definitely more relaxed about following arbitrary rules that no one observes, I internalised some of them and still can't bring myself to break them. It's the same way that I no longer give a shit about the dying less/fewer distinction and firmly believe that you can use whichever you please, but I myself am physically incapable of saying the "wrong" one.

[3] Famously having somewhat recently won a poll to remain the national flag despite such obviously superior competition as the laser kiwi.

[4] I actually just looked it up and predictably, both are considered correct and the Jack at sea thing is just a made up half truth, or more like a quarter truth. Unfortunately the punchiness is still lost by addition of this footnote.

[mothmute]

opinion: laptops/monitors/TVs advertising their size in diagonal inches is bullshit, the orthogonal dimensions are way easier to interpret for "will that fit in this space"

[violetfractal]

Working with a technique where each parent has its own modulus instead of one mod containing the sum of all the parents. For the menger sponge I got a nice texture on m=[3,3,3] since individual cells can now hold values as high as 2+2+2.

Cozy shades of umber

Same render at 243x243 cells

Letting each parent have its own modulus produces chaos, mostly. Here’s m=[3,2,2], which means a cell’s value is the sum of (left parent mod 3) + (middle parent mod 2) + (right parent mod 2).

Crispy!

When all three moduli share factors more order can emerge from the deep-fried chaos. Here’s m=[3,3,6].

Finally if I make just one of the three moduli very large compared to the others I get… motion blur?

m=[3,27,3] is booking it!

The render gives the appearance of motion because the diagonal parent is allowed to count to 26 while the orthogonal parents can each only count to 2. Along each diagonal, cells increment irregularly from 0 to 31 in the active zones but hold constant in the dead zones.

[focusonarchitecture]

Day 70 — Evan Walker Bridge

Formerly known as the Southbank Pedestrian Bridge, the Evan Walker Bridge is named in honour of the late Professor Evan Walker, a former planning minister who was integral to the development of Melbourne’s popular Southbank precinct. The Bridge is a bicycle and pedestrian bridge over the Yarra River between Southbank and the central business district in Melbourne.

A design competition was held for a pedestrian bridge, which would link Flinders Street Station and Flinders Walk with Southbank Promenade. The winning entry featured a steel tied-arch form, designed by architects Cocks, Carmicheal & Whitford.

The firm explains their design: "The significance of the river in the ordering of the southern city edge of the CBD and the intention to implement major river edge works of an urban character in this section of the river were seen to be the major design determinates.

The inherent differences between a bridge specifically designed for pedestrians and one that is primarily a vehicular bridge was explored, as was the presence of the existing bridges and their contribution to the river environment in this precinct.

The bridge design, as well as fulfilling its primary role as a means for people to cross the river, allows a further opportunity for it to become a passive recreational resource, a place on the river.

The configuration is of two jetties orthogonal to the river banks linked by a diagonal central span supported by an arch that is itself diagonal to the span. This is deliberate, accentuating the considerable lateral distance the bridge must accommodate to reach its respective landing points.

From the Southbank, direct views across the river are denied by a bluestone wall, rising sheer from the island below. The island is seen as a fragment of the nearby bank, complete with a tree notionally displaced from the Southbank landscaping.

Leaving the northwalk, the views are virtually unrestricted with the end of this section given over to a covered seating area isolated from the main foot traffic. A pylon loosely modelled on a rowing shell, a familiar form on this part of the river, supports this northern jetty and forms the springing point of the arch over the central span.

The arch, a traditional bridge form, supports the raking walkway at the midpoint on a steel triangle, a simple form that modestly attempts to establish a presence against a busy urban skyline.

At night two elements, the arch and the tree will be strongly illuminated and the rest of the bridge kept in relative darkness. The intention is that the seemingly inadequate dimension of the arch and the displaced tree reflected in the dark waters of the river will give the bridge a somewhat surreal quality."

Photo: 2021

[1-1sundial]

CANT believe they discovered a period 19 oscillator for conways game of life and i DID NOT HEAR ABOUT IT !

a refresher: conways game of life is something called a cellular automata. it consists of an infinite grid of cells which are either alive or dead. every step, update every cell all at once according to the amount of living adjacent cells (orthogonally and diagonally). if a dead cell has exactly 3 living neighbors, it becomes alive, and a living cell only survives if it has 2 or 3 living neighbors.

an oscillator, in conways game of life, is any pattern which repeats itself after some fixed amount of steps. for example, the blinker, the most common oscillator, will repeat after 2 steps:

the first generation is 3 cells horizontally, then the next generation is 3 cells vertically. then the generation after that is 3 cells horizontally again; it repeats! it repeats after 2 steps of simulation, so it is called a period 2 oscillator.

here's a more complicated oscillator, the period 15 pentadecathalon:

now, for high enough periods, there is actually a general solution for making an oscillator of any period you want. there's a pattern called the glider; it is the simplest and most common spaceship, a spaceship being any pattern which moves in a direction:

there's also a pattern called the snark, which basically just sits there and does nothing until a glider hits it from a specific direction. when that happens, it causes a reaction which leaves the snark unharmed and reflects the glider 90 degrees. if you set up a bunch of snarks bounding gliders around in a loop, you can create an oscillator of any period you want by adjusting the size of the loop. the smallest period this works for is period 43:

you can't go lower than 43 because that's how many steps it takes for the snark to be ready to reflect another glider, and nobody has found a way to reflect gliders faster than that. still, that means you only need to find oscillators for 42 different periods, and then you'll have proven that an oscillator exists for every single possible period!

before july 14th, there were only two periods for which they hadn't found any oscillators: period 19 and period 41. they still havent found a period 41 oscillator, but they have found a period 19!

this is what it looks like! it is called "cribbage" and it was discovered by a guy named mitchell riley. it is SO silly.

[tehamelie]

You know, if Rowling had had any real wit or courage there should have been an Orthogon Alley to intersect with Diagon Alley. I don't doubt that she knows the word, and it would have been the obvious way to go with the pun names, but it would run the risk of not making readers feel clever as they might have to look up this ten dollar word and writing for the broadest possible appeal was a priority

[blueeyedrat]

Steam Next Fest, fall 2024. A quick one this time, but still a few games worth discussing. More thoughts under the cut.

I don't play point-and-click adventures that often nowadays. Always had other stuff on my plate, I suppose. But if I do ever feel the urge to get back into the genre, Loco Motive might be a good one for it. The writing and voice work are spot on, the pixel art is good, and the puzzles in the demo never felt too obtuse. And who doesn't love an old-fashioned train murder mystery? Worth keeping an eye on, I think.

The puzzle games I tried out were a mixed bag. There were a few that seemed alright but didn't really hook me (Toggle Tile, CLONY, The Valley of the Architects), and at least one that definitely did (Block Shop; like I've said before, it's hard to go wrong with conveyor belt puzzles).

The Book of Buja left a good impression. It's a top-down adventure, kinda old Zelda-ish for better or worse. The movement feels kinda restrictive, but not to the point where it becomes a problem in combat (you can only move orthogonally, but your spear has a deceptively wide arc so you won't get caught on diagonals). It seems rather puzzle-focused in a way I appreciate, with some familiar tools and some unique mechanics that I'd like to explore more in the full game.

Likewise, Glitch Dungeon Crystal has the makings of a solid puzzle-platformer, with an interesting set of powers to use and things to interact with, that play off of each other in satisfying ways. The glitchy aesthetic may not be to everyone's taste, but fortunately there are options to tone it down a notch so it's easier to parse.

If you're looking for another city-builder to throw on the pile, the classical Greek-themed Polismós might be worthwhile. It didn't draw me in as much as some others in the genre, but there's some potential there.

I also tried out a couple of the more puzzle-oriented builders. Cosminomy had an interesting hook (building up multiple miniature planets) but didn't quite land for me, being more akin to an idle game where you spend your resources to unlock more places to build on and earn more resources, and felt kinda bare outside of that. Dorpie is more focused in some ways (working towards objectives to earn new building pieces) and more freeform in others (you can use any piece you have available at any time, rather than a limited queue of pieces), which works out to something that still feels unique and lets you build some nice-looking, blocky constructions.

I'm torn on TetherGeist. This is a precision platformer that wants to be like Celeste: vibrant pixel art and music, a strong narrative and cast of characters, and gameplay that's challenging but still accessible. I think it succeeds at most of these goals. That last one is a problem. The main gameplay gimmick sounds interesting in theory, but in practice it quickly feels overwhelming or inconsistent or both. Something about it just didn't click for me.

Closing out with the one title that was already on my Steam wishlist, Symphonia. I wish I had more to say about this one, but the demo was much shorter than I was expecting. What I did get, though, I liked a lot; the visuals and audio are excellent, and the platformer gameplay is loose in a fun way, particularly in wide open spaces where you can bounce off the walls and launch yourself in large strides. One more to look forward to.

[inhumanliquid]

Tbh rook vs bishop discourse only exists because people think diagonal movement is more important than orthogonal. Like have yall forgotten the rook has an important role in king safety, but bishops? What special ability do they have, homophobia?

Huh

[dailycharacteroption]

Conversion Corner: Even More Bloodstained Spells part 5

Va Ischa

We end off the series this week with one final spell, one of the handful of more spell-like shards that have names in a strange primal tongue (which might be enochian or some derivative of latin in-universe but was explained as being anagrams for foods in an interview.)

In any case, the va ischa is a spell granted by the forneus enemy, a demonic fish with far too many eyes. I forget if forneus is actually capable of casting the spell itself, as they are fairly easy to kill even before you get the upgrade that lets you move in water freely.

The va ischa shard conjures a ring of icy shards around Miriam, which then fire off in rapid succession in the orthogonal and diagonal directions, potentially striking many foes when surrounded. With that in mind, we can probably create a spell that strikes at foes outwardly from the caster.

Ice Scatter

School evocation [cold]; Level bloodrager 4, magus 4, occultist 4, shaman 5, sorcerer/wizard 4

Casting

Casting Time 1 standard action

Components V, S,

Effect

Range self

Area 30 ft radius burst centered on self

Duration instantaneous

Saving Throw Reflex half; Spell Resistance yes

Description

Shards of ice spray out from your body in all directions. Other creatures within 30 feet of you must make a Reflex save or take 1d6 cold and slashing damage per caster level (max 15d6).

An extremely simple spell, somewhat similar to detonate, but since there is no delay or risk of also taking damage, the damage is more traditional d6s rather than d8s. Having it be half slashing damage also makes it easier to resist, hence having a higher dice cap.

[isaackuo]

Bresenham Roguelike Movement

Typical roguelike AI uses a simple 8 directional homing algorithm:

(vx,vy) = (sign(dx),sign(dy))

where (dx,dy) is the vector from the monster to the player.

What if we want something more like a straight line path to the player?

The intuitive solution is to use fractional subpixel movement, but this can result in monsters moving in a jagged way rather than using diagonals.

Instead, we can use Bresenham's line algorithm to reduce jaggies.

(vx,vy) = (sign(dx),sign(dy))

R=R+min(abs(dx),abs(dy))

if R>0 then

R=R-max(abs(dx),abs(dy))

else

if abs(dx)<abs(dy) then vx=0 else vy=0

In this algorithm, R is the "remainder" that keeps track of how far above or below the current cell is to the fractional "true" position. This difference is R/max(abs(dx),abs(dy)).

Now, if this were the true Bresenham line algorithm, then dx and dy would remain constant, and there would also be an initialization factor setting R to optimize the line fitting.

But in this case, dx and dy usually change every turn. To compensate, we should recalculate R each turn based on the true fractional value, but I say don't bother. As long as max(abs(dx),abs(dy)) changes somewhat smoothly, it's not really going to be a big deal. Also, R should change if the octant changes. But again, who cares?

The bottom line is that this modified Bresenham algorithm will always choose either the diagonal or orthogonal direction most directly toward the player, while fractional subpixel movement can result in orthogonal movement that is less toward the player.

[tangleworm]

NOMIA Devlog 3 -- Diagonals

(Been working on the mix of enemy generation, but I haven't done the art for many of them yet!)

There's lots of weird stuff that happens when your game is tile-based, like how to handle movement and knockback.

There's lots of ways to handle "distance" in a tile-based world. You could make it so that 1 unit of movement lets you step left, right, up, or down -- this is called rectilinear distance, or Manhattan distance. Fire Emblem does this. You could make it so that a unit of movement also lets you step diagonally -- this is called chessboard distance, or Chebyshev distance. Many D&D battlemaps do this.

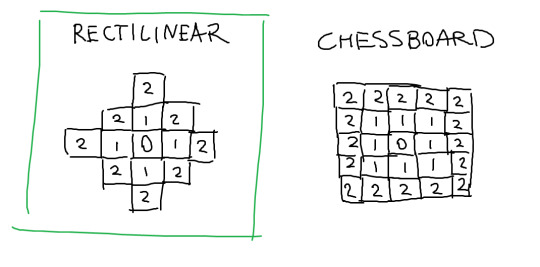
I decided to go with rectilinear distance for this game, since it's more intuitive when we consider distances in the real world. This means that going diagonally costs 2 points of movement -- an attack with a range of 2 will only be able to target the immediately adjacent diagonal tiles.

However, certain attacks can move the caster (lunging and retreating), the target (knockback and pull-in), or both. There are a number of ways we can make a "line" from one point to the next in rectilinear geometry. How do we handle non-orthogonal pushing and pulling?

I could think of three ways to handle it.

1. Don't

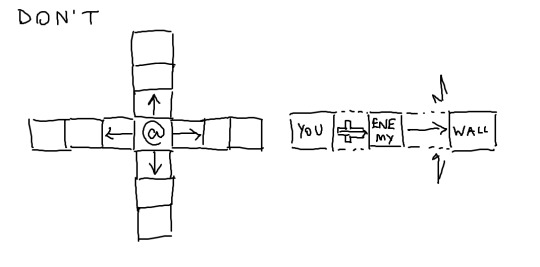
If we restrict any self/target-moving abilities to just the orthogonal tiles, we can sidestep the whole issue. This is simple to implement, and the player will always understand exactly how knockback will work, because it only happens when we can count exactly how many tiles everything will move.

The downside to this is that this cross-shaped target can get extremely annoying when you want to hit an enemy that's directly diagonal to you. Because movement costs an action point in this game, it can get annoying to have to spend that point to do a very minor positional adjustment to hit an enemy that already "feels" adjacent to you.

2. Kinda Do

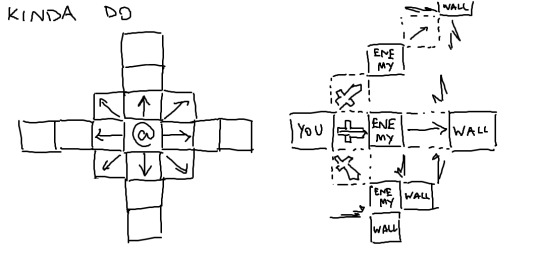
If the target is at exactly 45 degrees, it only gets a little more complicated to understand, but it gets a lot less annoying at close ranges. Every diagonal tile needs 2 units of knockback.

The tricky part is handling the different corners an enemy can get knocked into. Because knockback does damage based on how much remaining knockback there is when the unit hits a wall, how do we handle when it hits a corner, but there's only 1 unit of knockback left? How do we handle them hitting a convex corner (e.g. being shoved into the corner of a building from the exterior) versus a concave corner (e.g. being shoved into the corner pocket of a pool table)? Can we make this intuitive for the player to understand?

3. Really Do

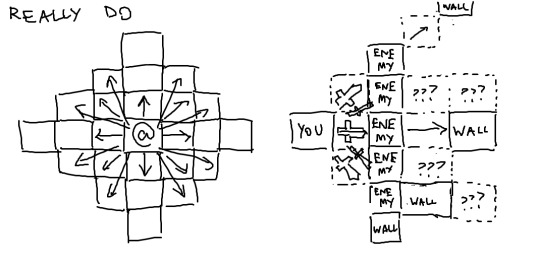
We can go all the way and let knockback abilities hit every tile a non-knockback ability can.

This is difficult for both the developer and the player, since there are many ways to form a line (i.e. the shortest distance between two points) when we're in rectilinear space. Should we snap the knockback to the closest direction? Should we push the enemy on a path that might not be what the player wanted? Should we let the player choose, and slow down the decision for every knockback card by an extra click? Even this diagram is complex to look at, and we haven't even gotten into handling convex corners versus corner pockets.

It didn't seem worth it for the tradeoffs.

In the end: I originally went for Don't, but after some consideration I'm partway through implementing Kinda Do, and I'm happy with this choice. It prevents knockback-related abilities from feeling underpowered due to needing to spend an action point on a minor positional adjustment before casting them, and most knockback abilities are close range anyway.

If anything, this shows how much thought must have went into the various tile-based worlds we've seen before.

[rhodesmusic]

The boundary of a tricylinder is a rhombic dodecahedron: graphing polyhedra with implicits and expressing them as Minkowski sums

The day before yesterday (or rather, yesterday at 12 in the morning) I was mathing on discord and a friend brought up Steinmetz solids, which are funny shapes obtained by taking the intersection of two or three cylinders. As the cylinders pass through each other, they outline a shape where they cross, which is the Steinmetz solid. Taking two cylinders gives you something called a bicylinder, and similarly, taking three cylinders gives you something called a tricylinder:

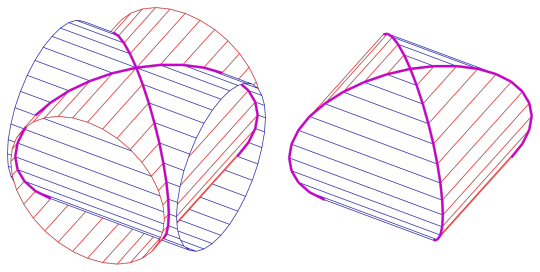
Images from Wikipedia

They showed me this and I was interested in the diamond-like pattern of the corners and edges on the tricylinder. Looking at it, we can see that the points at which all three cylinders intersect form a cube, and the other corner points come from where two cylinders intersect in the middle of the third, which seem to be positioned in the middle of the squares from the cube. Plotting this out and projecting the vertices onto a sphere to get a better idea of how they're arranged, I got this funny shape, which is called a rhombic dodecahedron, apparently:

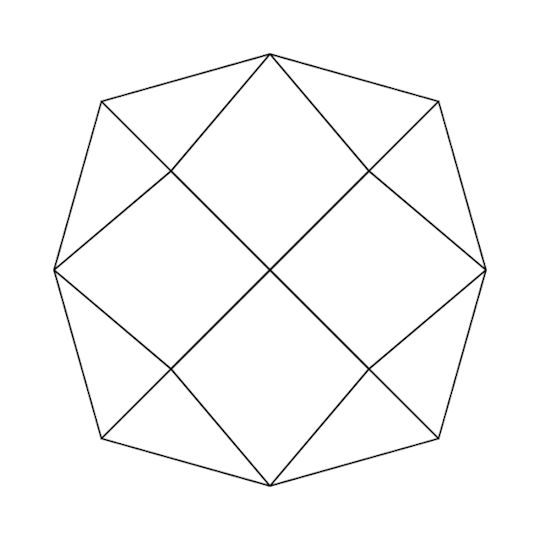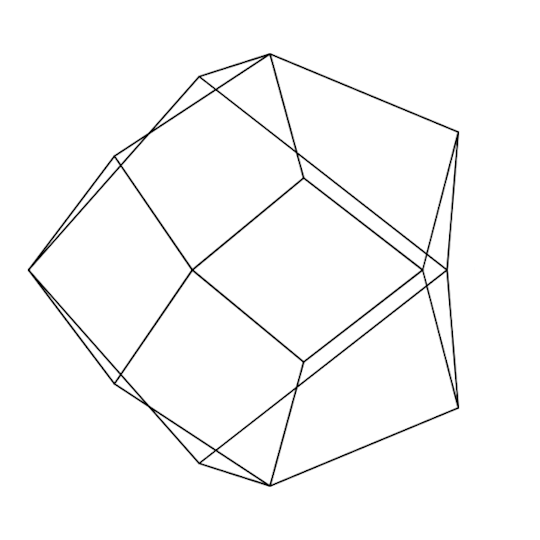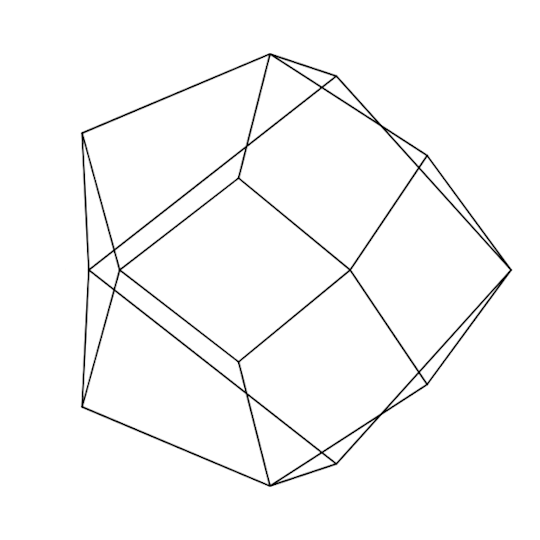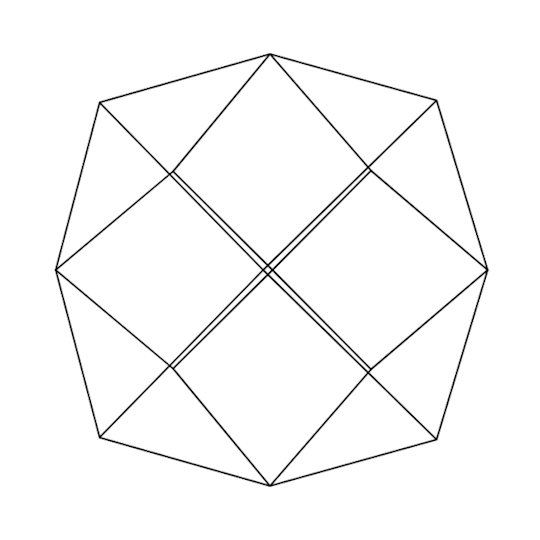
Made with desmodder for desmos graphing calculator, graph link

I guess the name comes from how all its faces are rhombuses and how it has twelve faces, the same number of faces as a dodecahedron. Sharing this with them, another friend's immediate reaction was "oh SHIT it's the"

along with this implicit plot of the rhombic dodecahedron in a 3-d grapher (a really cool one, by the way) (also, not the exact image they sent, just recreated it lol). What immediately caught my attention was how simple this implicit equation was. It seemed awfully convenient how this complex shape could be described so concisely with an implicit. I looked up the rhombic dodecahedron on Wikipedia, and found that it was, in particular, a zonohedra, which is a competitor for the most fuckin silly math term of all time.

A zonohedra is a convex polyhedron which is centrally symmetric, possessing a special kind of symmetry, but what's sick is that a zonohedra may be equivalently described as a Minkowski sum of a collection of line segments. A Minkowski sum of two shapes is just the shape you get when you take any point from the first and add it to any point in the second, via vector addition. You can repeat this to get the Minkowski sum of any number of shapes in any number of dimensions, and when the shapes are all line segments, you get a zonotope (lmao).

Thus, 3-dimensional zonotopes are these zonohedra, which come from taking some number of line segments in 3 dimensions, and then going through all combinations of points on them, picking one point for each segment, and adding them together. The rhombic dodecahedron turns out to be the Minkowski sum of the line segments forming the long diagonals of a cube, and I can't help but feel like the simplicity of it's implicit equation comes from how it can be expressed as a zonohedron.

(Me realizing the rhombic dodecahedron is a zonohedron)

Thus, I'm interested in how you could get from a zonohedron to a Minkowski sum, and then to an implicit plot, or maybe the other way around from an implicit plot to a Minkowski sum (though this requires you know the implicit gives a Minkowski sum to begin with). For example, any cube is the Minkowski sum of three orthogonal line segments of equal length (letting the lengths vary gives you a cuboid), and the unit cube has the implicit equation

max(abs(x),abs(y),abs(z))=1,

so I wonder how you could derive the implicit from the Minkowski sum. (Unfortunately, the cube is the only Platonic solid that's also a zonohedra, since it turns out that the faces of a zonohedron have to have an even number of sides, so womp womp for expressing the tetrahedron, octahedron, icosahedron, or dodecahedron as Minkowski sums of line segments.)

Note how it doesn't matter if you translate a shape in any direction when taking the Minkowski sum, since the resulting shape will be congruent to to what it'd be without translating, namely, it'll just be that shape translated in the same way the component shape was. This means you can translate the line segments in a zonohedron's corresponding Minkowski sum so they all sit at the origin, so that every one of them can be described with the vector sitting at the end of the line segment; the zonohedron can be derived from just a collection of vectors. This site I found gives these vectors for lots of different zonohedra.

So, given some 3-dimensional vectors, how would you get an implicit equation plotting the zonohedron they represent? I'm working on this for the 2-dimensional case, with the goal of being able to bump it up to 3-d or even generalize it to n-dimensions once I figure it out.

Also, another thing I'm mildly curious about. In my opinion, the tricylinder is much more cool and swag than the bicylinder because the 3 cylinders it comes from make full use of 3-dimensional space and thus we get a cool polyhedron from it (the bicylinder gives you something called a hosohedron). An infinite (filled-in) cylinder can be thought of as the Cartesian product of a disc with the real line, for example, for an infinite cylinder around some axis, you take a disc orthogonal to that axis and sweep it back and forth along the axis.

This proposes a generalization of the tricylinder: In n-dimensional space, take n copies of the Cartesian product of an (n-1)-ball with a line. Namely, for each axis from the canonical basis, take the unit (n-1)-ball sitting orthogonal to that axis and sweep it back and forth, getting a (filled-in) "hypercylinder" (don't know if this is the actual name for this). If we take the intersection of these hypercylinders, what's the n-dimensional polytope we get from the boundary of the intersection, that is, the graph we get from the boundary? (How to even define this boundary graph, that is, define what the vertices and edges are in a way that generalizes to n-dimensions is the first step).

For 2-dimensions, the 1-ball is just a closed interval, and the cylinders are just infinite strips, so the intersection is the filled-in unit square and the boundary is a square. The boundary of the Minkowski sum of 4 line segments, starting at the center of a square and ending at its vertices, is also a square. Similarly, for 3-dimensions as we saw we get a rombic dodecahedron, which is equivalent (as a graph) to the boundary of the Minkowski sum of 8 line segments going from the center of a cube to its vertices.

If this pattern continues, which I feel like it should, it'd give an equivalence for this question, namely, the n-polytope coming from the boundary of the intersection would be equivalent (graph-isomorphic) to the n-polytope coming from the boundary of the Minkowski sum of 2^n line segments, going to the vertices of the n-hypercube. (Note that we could just take 2^(n-1) line segments going to just the vertices of the top half of the hypercube to get an equivalent shape up to some translation and dilation, this is what the website I linked five paragraphs ago does.)

That's all for now. Will post an update on this if I find somethin!