utherciveng

[utherciveng]

Geometric Characteristics

Moments of inertia

First moment of area = CENTROID x AREA = Static moment (Syo or Zyo)

Sx = ∫ydA = A*yc ---> yc = Sx/A (yc is the y coordinate of the centroid from the x axis)

Sy = ∫xdA = A*xc ---> xc = Sy/A (xc is the x coordinate of the centroid from the y axis)

Second moment of area; Area moment of inertia

Ix =  ∫∫y2dA (y is the coordinate of the object from the x-axis)

Iy = ∫∫x2dA (x is the coordinate of the object from the y-axis)

Moment of inertia; similar formula but different definition. Uses mass instead of area

Ix =  ∫y2dm (y is the coordinate of the object from the x-axis)

Iy = ∫x2dm (x is the coordinate of the object from the y-axis)

Units of moment of inertia is in [kg m2]

CM - Center of mass of an object.

Parallel Axis Theorem

I = ICM + Ad^2

ICM is the moment of inertia of an object relative to it's center from the analysed axis.

d is the perpendicular distance from an object's center to the axis.

A is the area.

Note: It normally helps to write the object center coordinates down on the diagram as you solve it.

Useful equations to know:

I always find it better to learn from examples. Below are 2 solved examples.

Oh yeah, happy Easter everyone! Hope y'all are having a good one.

Cheers

[utherciveng]

Torsion Revision Notes

Subject: For a beam fixed on one side

Procedure:

Draw moment of torsion diagram Mx.

Memory prompt: For notation symbol used, think of dot in circle as an eye. The eye above the surface is an evil eye which = (-) Negative value.

Determine the cross-section by using relationship: θmax ⩽ θall

where θall is already given, and θmax = Mmax/(G*Ix)

(Need to know Ix = (π*d^4)/32, and substitute into θmax)

Do for each section if there is a change of diameter, or do it only once if the beam has the same cross-section

Calculate Ix (moment of inertia), for circular cross-section: Ix = (π*d^4)/32

Calculate maximum shear stress, τmax = Mxmax/ωx

ωx = Ix/radius

Verification: τmax < Rt

Calculate and draw unit angle of twist diagram

Formula: θ = Mx/(G*Ix)

This is the same shape as the torsional moment diagram Mx

Calculate and draw angle of twist relative to fixed end diagram, α

α = Area of θ diagram section

Subject: Beam with both ends fixed

Procedure:

Determine one of the unknown reactions.

Usually the one on the left side. A beam fixed on both ends is statically indeterminate and requires the extra condition αA/E = 0.

αA/E --> That is, the angle of twist relative to the fixed end, from the start to the end of the beam.

Form Mx equations for each section. Starting from one end and building up as we go.

Normally cut in the middle of a section, and let x start at the beginning of an analysed section.

Ex: MxAB = MA, MxBC = MA - 10, MxCD = MA - 10 + 4xc.

For each section the Mx equation is integrated, as α = ∫θdx = ∫ (Mx/G*Ix)dx

The lower bound is always 0 (if x is newly defined at the start of each section) and the upper bound is the length of the section.

Solve αA/E = 0 for unknown reaction (MA in this case).

Continue procedure for "Beam with one end fixed"

[utherciveng]

[utherciveng]

Tension Practice Problem 2

[utherciveng]

Tension Practice Problem 1

If the notes are hard to see right-click the image and go "open in new tab". You can zoom in even more there or download it if ya like. I don't mind.

Welp some morning study done. Time for a break~

[utherciveng]

Tension Revision Notes

Subject: For a beam fixed on one side

Procedure:

Draw Axial diagram (start from free end that's not fixed)

Calculate diameter based on relationship: σmax ⩽ R (knowing that σ = N/A)

Calculate separately for each section when there's a change in diameter

Make sure to round up for safety.

Calculate and draw the stress distribution, use formula σx = N/A

Calculate the strain distribution (drawing it is optional). This is generally the same shape as for stress, but with different values calculated with formula εx = σx/E

Calculate and draw the displacement scheme:

u = ∫εx dx , This is the relationship used.

Elongation at fixed end is zero, △ = 0

Integrate each section based on the strain and add it up on the diagram.

Note: When something is integrated the order is increased. Constant becomes linear. Linear becomes a curve, etc.

Early check for stress diagram: Values need to be within the range (-R, +R) MPa

Subject: For a beam fixed on both sides

Procedure:

Know that elongation is impossible in this case and that △ = 0 for the whole beam.

Sum the elongation for all beam sections:

△ = △AB + △BC + △CD

△AB + △BC + △CD = 0 <--- The equation that we use to solve for an unknown reaction

Build Axial (N) equations for each section by starting at one end and summing the forces as we go. Cutting exactly in the middle of each section.

ex: NAB = -HA

NBC = -HA + 2P

NCD = -HA + 2P - P = -HA + P

Knowing these N equations, use the formula from Hooke's Law: △H = (N*L)/(E*A)

Using △ = 0 equation, solve for the unknown reaction, in this case HA.

Continue from step 1 of the procedure for beam with one end fixed.

Subject: Truss

Procedure:

Truss analysis: Method of sections + Method of joints (if needed) to find necessary Axial force values for members

Determine which is Nmax (the maximum axial force)

Find the area, A, of the cross-section using relationship:  σmax ⩽ R (knowing that σ = Nmax/A)

Solve for maximum stress: σmax = Nmax/A

For solving the elongation of a section, use formula △H = (N*L)/(E*A)

+ means expansion of a beam, - means shrinking of a beam

Vector black magic:

Draw axis u-v origin at point that moves, in this case point B.

Define e1 = (cosα, sinα). Here e1 = (0.8, 0.6) --> Which goes along segment BC

Use elongation formula, △H = (N*L)/(E*A)

△AB = (NAB*L)/(E*A), △BC = (NBC*L)/(E*A)

Use this formula: uB*cosα + vB*sinα = △

Apply this to the segment where a known unit vector goes in the same direction.

Thus, using segment BC as the coordinates for e1 is known and △BC has been calculated.

We now have: uB*(0.8) + vB*(0.6) = △BC

This equation can't be solved, so we move onto e2.

e2 goes along segment AB which, according to the u-v axis, has an angle of 180°. cos(180°) = -1, sin(180°) = 0

It's easy to see now that e2 = (-1, 0). We substitute in now

uB*(-1) + vB*(0) = △AB

uB*(-1) = △AB ---> uB = - △AB

We now know the horizontal displacement and can solve for the vertical displacement of point B with the previous equation.

[utherciveng]

"Holy shit this is useful" Links

To be updated whenever I find more stuff.

Moment of inertia table with diagrams and formulas.

Strength of materials book with some sections that might be of interest:

65 - Principal stress and strain 112 - Moment of inertia and centroid 276 - Torsion

[utherciveng]

Yes

Thank you Tumblr editor for being very consistent with the font colour. Very nice yes

[utherciveng]

Hello World, noob coder

Jasne, jestem noob w kodowaniu który chce się uczyć Python 3. Wiec najlepszy sposób jest pisać coś dla projektu. Szczególnie, dla najgorszego przedmiotu teraz, wytrzymałość materiałów. Ugh, diabeł jest lepiej.

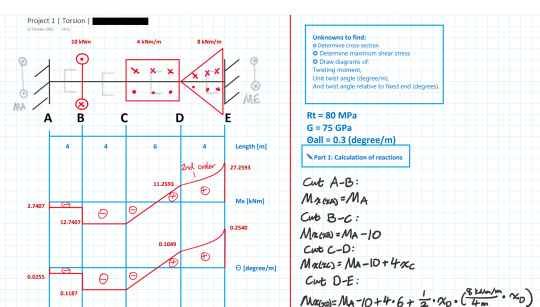
Pierwszy projekt na 2. semestr, skręcanie.

Ostatnio pisałam coś na początku projektu. Mamy równanie na moment skręcający segmentu, a potem to integrujemy!

Tutaj jest mój kod dla tego celu:

from scipy.integrate import quad from sympy.abc import z

s1 = float(input("Please enter the length of the 1st segment in m: \n")) MR = z low = int(0) # lower bound of integral

print("\n")

print("Next section: Defining moment equations") p1 = str(input("Enter the polynomial for the moment of the 1st segment in terms of x: \n"))

def Integrate(x): # Defining the function Integrate() which integrates code return eval(p1) # eval() evaluates string as Python code

print("-------------------------------") print("Result of integration: \n") alpha1 = quad(Integrate, low, s1)

beta1 = alpha1[0] + MR*s1 # adding unknown reaction MR (from left fixed support) print(beta1) # this is our integrated moment equation now

Eh, prosty ale to działa. Będę pisać więcej później ale najpierw mam test że muszę studiować. Chyba będę dzielić się tutaj ale moje notatki będą po angielsku.

Miłego dnia wszyscy