wiskwa-en

[wiskwa-en]

A metaphor in search of something real

[wiskwa-en]

It is really about infinite maximal almost disjoint families though.

[wiskwa-en]

Much ado about Set Theory and Machine Learning.

[wiskwa-en]

KP saw a hole

On twitter I got involved in a discussion about holes, in particular the number of holes in a drinking straw (in Dutch). The answer depends, of course, on what you deem to be a hole but when you involve mathematicians in the debate the the answer that you will get is `one'. And that is because mathematicians have a very precise definition of what constitutes a `hole' and that definition leads to that answer.

Meanwhile this discussion also reached Australia where in a street poll 58.6% decided a straw has two holes.

So, what is a hole?

We (that is the mathematicians) consider a straw to be a surface and we count the number of holes by drawing curves on the surface that begin and end in one fixed point, also called the base point. On a real straw that becomes cumbersome so we imagine we have a straw made from very flexible material and we stretch it on one end so as to turn it into a ring-shaped area in the plane; there it is way easier to draw curves. You can make the curves also out of string or elastic bands; that save on erasing when the paper becomes too full.

Some curves can be shrunk to the base point while staying completely inside the ring. For other curves that is impossible, for example if you loop the string once around the hole in the ring (withershins). A curve that cannot be shrunk to the base points without leaving the ring-shaped area indicates that there is, mathematically speaking, a hole in our area. We could, of course, go more often around the hole, in both directions but that does not mean that we have infinitely many holes. One can prove (and it takes a bit of work that every curve can be deformed into the one curve that goes around the hole once. And in that process the number of times the curve goes around the hole is preserved; so a curve that goes around the hole three times can be deformed to three times that basic curve, while also keeping its orientation (clockwise or counterclockwise). This means that all curves can be reduced to a multiple of one base curve and that is why we speak of one hole.

A T-connection

Later in the discussion this picture appeared: two conjoined straws that made a T-connection. That contraption has three openings but mathematically speaking it has two holes. Thanks to the new 280 character limit you can squeeze that into just one tweet:

Bend openings 1 and 3 to the left so that you get a pair of pants; shrink this to a pair of swimming trunks. Put that on the table while stretching opening 2 so that it becomes the outer edge. Smooth it out: a disc with two holes.

There are now indeed two base curves: take a point somewhere in the middle and draw one curve counterclockwise around the hole on the left and one round the hole on the right. Every other curve that begins and ends in the base point can be deformed into one that only traverses the two base curves. Things get a bit more complicated because the order really matters: first left then right is not the same as first right then left.

Holes in the cheese

Holes in the cheese cannot be detected with curves; it is relatively straightforward to deform every curve into your base point while avoiding all `bubbles'. In this case you can use (virtual) balloons: a balloon that has a bubble inside it cannot be deformed to the base point while staying completely in cheese territory. One can even count the holes using base balloons and define how every balloon can be deformed into a combination of base balloons but that is much more involved than in the case of curves.

[wiskwa-en]

Slides of a lecture with the title `What is finite?'.

[wiskwa-en]

A `mathematical’ problem (part 2)

The original version of the previous post elicited a lot of reactions on twitter. This post contains some comments on (and inspired by) these reactions.

1. Some people gave 13 as the answer for 5+8, justifying this by saying that the second and third equalities were false. I think this actually the most sensible solution: if you write `+’ then you must mean `addition’; don’t be silly.

2. The answer suggested most often is 45 and the reasoning is mostly something like the differences are 7 and 9, so going from 3 to 4 it will be 11 and from 4 to 5 it will be 13, and that makes 45 the likely outcome for 5+8.

2a. Alternatively you can try to reconstruct/divine the new meaning of `m+n’; most people came up with `the sum of m*n and m’ (do not write m*n+m because + does no longer mean `add’), this also leads to 5+8=45.

2b. Another answer that came up quite often was 32: that solution simply skips 4+7 and uses 11 to get from 21 to the answer 32.

2c. An other popular answer is 34, the explanation being “you add the true outcome of the addition to the previous answer”. If you were to apply this to the intermediate 4+7 as well then the answer would, again, be 45.

3. In the mathematical magazine Pythagoras, in the issues of April 2009 (The IQ formula) and June 2009 (IQ formula light), you will find an explanation of how to systematically create a formula that describes a given finite sequence of numbers and thus how to find the next term(s) of that sequence. In spite of what the titles of the articles suggest this will not let you necessarily do well on IQ tests because the method does not take any creativity of the makers of the test into account. Oh, and the articles are in Dutch but with some perseverance you will get the mathematical gist of the arguments.

4. The formula from the previous post, the one that gives 5@8=4754660328285, is basically a very contorted (perverse?) application of the method from Pythagoras.

5. In this book (pages 344 and 345) this type of problem is tackled statistically. Some Bayesian arguments are used to determine which of two possible formulas is most probable. But this author also warns that it will never be 100% clear what the poser of the problem was really thinking.

[wiskwa-en]

A `mathematical’ problem

The following `mathematical’ problem is doing the rounds on the internet.

Personally I am not a big fan of this kind of `problem’ because the purpose is not to determine the system behind the data, because there is no unique law that governs it, but whatever it was that was in the head of the poser of the problem.

My standard reply to such a question is: 0 (or sometimes 42, the universal answer from The Hitch-hikers Guide to the Galaxy). Can we say something sensible about a problem like this?

Let us see. For starters: the function of + is clearly not that of addition (if = is supposed to mean equality); this suggested to many people to replace it by some other symbol, @ say. The question then is: is there an operation @ that produces for every pair of natural numbers m and n a natural number m@n and in such a way that 1@4=5, 2@5=12 and 3@6=21? And if yes then what is 5@8?

For a mathematician the answer is clear: apart from the three demands we are free to do as we please, so the answer is “yes” and 5@8 is not determined it can be what we want it to be. For eaxample: define m@n=0, except in the three prescribed cases; that justifies my standard answer. If we separately define 5@8=42 then Deep Thought’s universal answer becomes correct.

Most people do not expect an answer like the two given above but rather a `formula’; some expression with m and n in it that `predicts’ what 5@8 should be. Formulas like that are plentiful. If you look at the data then the three equations are of the form m@(m+3)=x, so it could very well be that the operation simply works with the first coordinate only.

We have three values and these can be fitted by a quadratic polynomial in m alone. You can check that m@n=m2+4m meets our three requirements (plug in m=1, 2, 3). That will produce the answer given by most of the internet: 5@8=45.

With a little twist you can make infinitely many formulas that give the three desired outcomes all produce different results for 5@8. The trick is to find something that produces the value 0 when you substitute 1, 2, or 3 for m and only then. You can take (m-1)(m-2)(m-3). Using that we can produce infinitely many formulas: for every natural number k define m@kn=m2+4m+k(m-1)(m-2)(m-3).

With some tinkering it should be possible to make formulas that have 5@8 take on any value you like; I’d say: get to work. Here’s an example.

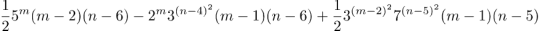
It produces 5@8=4754660328285.

To those who want to know if the sequence 5, 12 21 has any `natural’ extensions I recommend the On-line Encyclopedia of Integer Sequences; put the sequence in the search box to see what’s available.

[wiskwa-en]

The Intermediate Value Theorem, II

This is part two of a translation of an article that appeared in the February 2007 issue of Pythagoras.

The completeness of R, the set of real numbers, is the key to many theorems from Mathematical Analysis. You can use it to prove that many equations have a solution.

The Theorem

Can we distill a general theorem from yesterday’s post about the equation cos(x)=x? Yes we can and that theorem was formulated and proven in 1817 by the Czech mathematician Bernard Bolzano in an article with the wonderful title Rein analytischer Beweis des Lehrsatzes, daß zwischen je zwey Werthen, die ein entgegengesetztes Resultat gewähren, wenigstens eine reelle Wurzel der Gleichung liege. Here is the theorem, in Bolzano’s own words:

Lehrsatz. Wenn sich zwey Functionen von x, f(x) und φ(x), entweder für alle Werthe von x, oder doch für alle, die zwischen α und β liegen, nach dem Gesetze der Stetigkeit ändern, wenn ferner f(α)<φ(α), und f(β)>φ(β) ist: so gibt es jedesmahl einen gewissen zwischen α und β liegenden Werth von x, f&uumlr welchen f(x)=φ(x) wird.

(Very) freely translated: when two functions are continuous on an interval [α,β] and if in addition f(α)<φ(α) and f(β)>φ(β) then the equation f(x)=φ(x) has at least one solution between α and β.

There is one thing still undefined: what does it mean for a function to be continuous? Bolzano was probably the first to give a proper definition of that.

Nach einer richtigen Erklärung versteht man unter der Redensart, das eine Function f(x) für alle Werthe von x die inner- oder außerhalb gewisser Grenzen liegen, nach dem Gesetze der Stetigkeit sich ändre, nur so viel, daß, wenn x irgend ein solcher Werth ist, der Unterschied f(x+ω)-f(x) kleiner als jede gegebene Größe gemacht werden könne, wenn man ω so klein als man nur immer will, annehemen kan.

Translated freely: one says that a function f(x) varies for all values of x according to the laws of continuity if for each value of x the difference f(x+ω)-f(x) can be made smaller than any given magnitude by taking ω small enough.

In a more strict formulation, given by Weierstraß: for any given positive number ε there is an other positive number δ such that whenever |y-x|<δ one has |f(y)-f(x)|<ε.

Yesterday’s example dealt with f(x)=x, φ(x);=cos(x), α=0, and β=1. Both functions are indeed continuous. In both cases we can always take δ=ε, for we showed that always |cos(y)-cos(x)|≤|y-x|, so that if |y-x|<δ then |cos(y)-cos(x)|<ε.

The proof

The proof of the theorem is much like yesterday’s proof. We let A={y: α≤y≤β and f(y)if |y-x|then both |f(y)-f(x)| and |φ(y)-φ(x)| are smaller than ε (apply the definition to f and to φ and take the smaller of the two δs that you get).

Because x is the least upper bound of A there is y&in;A such that x-δ

Next take z such that x0.

This shows that -2εall positive ε and that means that f(x)=φ(x).

Squaring is continuous

Proving that a function is continuous is not always easy, as we saw with the cosine function: we needed a trigonometric formula and an estimate for |sin(y)|. Let us see how to show that the function g, given by g(x)=x2, is continuous. Fix x and a positive ε. How do we find a suitable positive δ?

Well, we first see what we can do with |y2-x2|, how we can relate it to |y-x|. We can factor it: |y2-x2|=|y+x|×|y-x|. That gives us |y-x| but there is also the variable factor |y+x|. Since we may take δ as small as necessary (as long as it is positive) we specify at the outset that it must not be larger than 1. Why? Because then |y-x|<δ will imply that |y-x|<1 and hence that |y+x| is less than the maximum of 2|x+1| and 2|x-1|, call that maximum M. This ensures that |y2-x2|≤M|y-x| when |y-x|<δ. Now we know how to specify δ given ε: take the minimum of 1 and ε/M;. Because then: if |y-x|<δ then |y2-x2|≤M|y-x| (because |y-x|<1) and M|y-x|

Conclusion: g(x)=x2 varies according to the laws of continuity.

Now let ψ(x)=2 (constant function), and α=0 and β=2. Then g(0)<ψ(0) and g(2)>&psi(2). So there is a solution of the equation g(x)=ψ(x) between 0 and 2. So Bolzano’s theorem shows the existence of √2 in an analytic, rather than geometric, way.

Why `Intermediate Value Theorem’?

Nowadays you will mostly see the the following theorem in many books:

Intermediate Value Theorem. If f is a continuous function on an interval [a,b] then f takes on all values between f(a) and f(b) on that interval.

It does not matter whether f(a)>f(b) or f(a)

This version follows from Bolzano’s version by comparing f with the constant function with value c.

The converse is also true: work with g=f-φ. Then g(α)<0 and g(β)>0, so there is an x between α and β such that g(x)=0, or f(x)=φ(x).

Re-reading. Now re-read this post and this post. There you will find proofs of the continuity of the functions x3 and 2x. And you will also see that we used the Intermediate Value Theorem to prove the existence of ∛2 and the logarithm.

[wiskwa-en]

The Intermediate Value Theorem, I

This is part one of a translation of an article that appeared in the February 2007 issue of Pythagoras.

The completeness of R, the set of real numbers, is the key to many theorems from Mathematical Analysis. You can use it to prove that many equations have a solution. Here we illustrate what it says by way of an example. Next time we discuss the general statement.

In the previous five posts we used the completeness of R, the number line, to prove that all n-th roots exist, that 2x exists for all x, and that we can make logarithms.

The number line is complete. Every non-empty set of real numbers that has an upper bound has a least upper bound.

In a few more words: if A is a non-empty subset of R for which there is an x such that a≤x for all a∈A (x is an upper bound) then there is an upper bound a* for A that is smaller than all other upper bounds.

Solving equations

We will use this property of the number line to prove that the equation cos(x)=x has a solution. When you look at the graphs of y=cos(x) and y=x then you will `see' that there is a solution, but a picture does not qualify as a proof.

At x=0 we see that x lies below cos(x) (for x=0 and cos(0)=1) and at x=1 we have cos(x) below x (for cos(1)<1). You would expect that the graphs intersect between 0 and 1 and that there should be a number α for which cos(α)=α.

To turn that expectation in certainty we can do two things. We can try to solve the equation is some way or another but when you try this you will find it hard to get a handle on the equation and that you are getting nowhere. The other thing we can do is prove that there must be a solution and give a way to get good approximations of α.

Finding a candidate α

Consider the set A={x:x<cos(x)}. This set is not empty, because 0∈A. The set also has an upper bound: 1∈A and if x>1 then certainly x>cos(x) (because cos(x)≤1).

This gives us a candidate for α: the least upper bound of A. For, just below α there are x-es with x<cos(x) and just above α there are x-es with x≥cos(x). This should imply that α=cos(α).

Proving that cos(α)=α

To prove that α=cos(α) we need a trigonometric formula, to wit

Using this we can deduce that cos(x) is close to cos(α) whenever x is close to α. The absolute value of the difference is equal to

And because the absolute value of the sine function is at most 1 we know that this is not larger than

Furthermore, as the picture below illustrates we always have |sin(y)|≤|y|

We find that always

With this we can show that cos(α)≥α and cos(α)≤α and hence that cos(α)=α.

Take a natural number n and pick x∈A such that x>α-2-n. We rewrite the difference cos(α)-α as the sum of three differences: cos(α)-cos(x), cos(x)-x, and x-α. Because |cos(α)-cos(x)|≤|x-α| we find that the sum of the three differences is larger than -2×2-n: cos(x)-x is positive and both cos(α)-cos(x) and x-α are larger than -2-n.

It follows that cos(α)-α is larger than -2×2-n for all n. But this then means that cos(α)-α is at least as large as the least upper bound of the numbers -2×2-n, which is 0. We find that cos(α)-α≥0.

Exercise. Show in the same way that cos(α)-α≤0.

An algorithm

We can now describe an algorithm to find approximations to α. What we do is cut the interval [0,1] in two halves, [0,½] and [½,1], and determine which half contains α. Then cut that half in halves, see where α must lie, and so on, until we are satisfied with the accuracy to which we have approximated α. A measure for that accuracy is the length of the interval that we find at each step. At step 0 (when we start) that length is 1-0=1, at step 1 it is ½ at step 2 we have ¼, …, at step i we have length (½)i.

It is easy to write a program for this: fix your desired accuracy ε, and set a0=0 and b0=1. Now repeat the following recipe.

set mi=½(ai-1+bi-1) and calculate cos(mi)

if cos(mi)=mi then PRINT "the solution is mi" and STOP

if cos(mi)>mi then set ai=mi and bi=bi-1

if cos(mi)<mi then set ai=ai-1 and bi=mi

if bi-ai<ε then STOP and PRINT "½(ai+bi) is the desired approximation"

the first `if' is there to see if we are lucky and have stumbled on the exact solution; the next two `if's ensure that always cos(ai)>ai and cos(bi)<bi and hence that α lies between ai and bi. The final `if' tests to see if we have reached the desired accuracy.

Exercise. How many iterations are needed when ε=1/1000? When ε=1/1000000?

The algorithm described above is known, for obvious reasons, as the bisection method. It will always give good approximations but it is not very efficiënt.

Next time we look at the general theorem that the above example illustrates.

[wiskwa-en]

Advanced logarithms

This is a translation of an article that appeared in the April 2006 issue of Pythagoras.

Last time we constructed the function 2x for all real numbers x. This time we consider its inverse function, the logarithm.

The function x→2x, that we defined last time, has all the properties that we expect of an exponential function. It is strictly increasing and for all x and y we have 2x+y=2x×2y. In this post we show that our function has an inverse function: the logarithm in base 2. We write the function as 2log and so, by definition

a=2log b and 2a=b

mean exactly the same thing. When we make an inverse function we exchange domain and range: the range/domain of x→2x becomes the domain/range of x→2log(x). We know the domain of x→2x: it is R the set of real numbers. We do not yet know the range; we know that the values lie in the interval (0,∞), but what we want, that (0,∞) is the domain of the logarithm, must be shown properly and we do this by showing the the range of x→2x is exactly the interval (0,∞).

So, given b>0 we must find an a such that 2a=b (and because x→2x is increasing there is exactly one such a). This we prove using the now familiar property of R: its completeness.

The logarithm

So, we have an arbitrary b>0. How do we determine a number a with 2a=b.

We first assume that b>1 and we let A be the set of all numbers x for which 2x<b. The set A is not empty because 20=1<b. The set A is also bounded from above: take a natural number k>b and note that 2k>k (this is not hard to prove for natural numbers). Because x→2x is increasing it follows that k is an upper bound for A: we cannot have x∈A and x>k holding simultaneously, for if x≥k then 2x≥2k>k>b and so x is not in A.

Like we said above, we use the completeness of R: every nonempty set with an upper bound has a smallest upper bound. Our set A therefore has an smallest upper bound, let's call it a. We show 2a=b.

We choose natural numbers m and n such that m<a<n, with m as large as possible and n as small as possible. Now we establish an important inequality:

if m<x<n then |2x-2a|≤2a|x-a|

For this we use the inequality from last time: if 0<r<1 then 2r-1<r. Now note that, because of the choice of m and n, we have |x-a|<1 whenever m<x<n. Now if a<x<n then 2x-2a=2a(2x-a-1)<2a(x-a) and if m<x<a then 2a-2x=2x(2a-x-1)<2a(a-x). And if we combine these two inequalities we get what we want.

Now if ε is positive and smaller than a-m then we use our inequality to deduce that 2a<2a-ε+2aε<b+2aε, and so 2a≤b

Likewise,if ε is positive and smaller than n-a then we use our inequality to deduce that 2a>2a+ε-2aε<b-2aε, and so 2a≥b.

We conclude that 2a=b. In case b<1 then we first find a such that 2a=1/b, then we have 2-a=b.

In summary: for every positive b there is exactly one number a such that 2a=b; that number is called the logarithm of b in base 2, we write a=2log b.

Exercise 1 Show that 2log(x×y)=2log x+2log y for all positive numbers x and y.

Exercise 2 Show that 2log(ap)=p×2log a if a>0 and is p is a rational number.

Other bases

Last time we also indicated how you can define the function x→ax for all a. We can also do that using just 2x and 2log x. In Exercise 2 you saw that 2log(ap)=p×2log a is p is a fraction. This means that

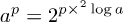
Because 2x and 2log x are increasing functions we can see that this should also hold for all x, that is

so, for example

This also gives us a logarithmic function alog: so alog q=p means ap=q. These logarithms are all related, as follows. From what we did above we see that if q=ap then also q=2p×2log a and so 2log q=p×2log a. But p=alog q and so if we swap the factors we get the following relation

Using logarithms

Logarithms were invented by the Scotsman John Napier (1550–1617) in order to perform large multiplications. That was done using the relation 10x×10y=10x+y. The use of 10 as a base is because it fits our decimal system better; in fact we usually write log x for 10log x. For example, to calculate 313.585×204.123 one would do the following

Step 1. Look up log313.585 and log204.123 in a table. Table usually give the logarithms of numbers between 1 and 10, so we first write 313.858=3.13585×102, so that log313.585=2+log3.13585. My table gives the following approximations: log313.585=2.4963 and log204.123=2.3071.

Step 2. Add the logarithms: 2.4963+2.3071=4.8034, this is the logarithm of the product.

Step 3. Now look up the x for which log x=0.8034 (approximately): x=6.359 and so 313.585×204.123 is approximately 6.359×104.

These days we would use a calculator for such a multiplication, but then we sometimes run into the limitations of our device. My calculator, for example, cannot calculate 70! (the product 1×2×…×70). When I ask for 69! I get 1.711224524×1098, but 70! yields Error. But with logarithms we can fix this: log1.711224524=0.233307995 and log70=1.84509804. The sum is 2.078405035 and 100.078405035=1.197857167. The 2 gives us 102 and so 70! is roughly 1.197857167×10100.

Exercise 3. Using the keys for log and 10x find an approximation of 100!; how many digits does that number have?

[wiskwa-en]

Advanced Power Taking, II

This is part two a translation of an article that appeared in the January 2006 issue of Pythagoras.

What is 2√3 exactly? In this post we shall give an exact definition of the exponential function 2x for all real numbers x. We also look at other bases for exponential functions.

We learned what what 2q means when q is a rational number; what about 2√3?. Because we cannot write √3 as a fraction we will have to come up with something really new.

We put the algebra aside and concentrate on an other property of the function q→2q: if p<q then 2p<2q; in words: taking powers of 2 is monotone.

This follows from the addition property: we have q=p+(q-p) and so 2q=2p×2q-p. Because 2q-p>1 we find that 2q>2p.

Exercise Show that, indeed, 2r>1 if r is a positive rational number.

We now intend to ensure that the function x→2x becomes monotone. For √3 this means two things: if p<√3 then 2p<2√3 and if p>√3 then 2p>2√3. The question then becomes whether there is a real number that meets those requirements, and preferably exactly one because then we do not have to choose: that one number will be the value of 2√3.

At least one

We are going to prove that there is at least one number x with the property that 2p<x<2q for all rational numbers with p<√3<q. For this we use the fundamental property of the number line that we used to prove that numbers like ∛2 exist:

Theorem Every nonempty set of numbers that has an upper bound also has a least upper bound.

In a few more words: if A is a subset of R for which there is an x such that a≤x for all a∈A (x is an upper bound) then there is an upper bound that is smaller than all other upper bounds.

We apply this to the set A={2p:p<√3}. This set does have an upper bound, 22=4, for example. So there is an upper bound, α, that is the smallest among all upper bounds. For this α we know that 2p≤α when p<√3, because α is an upper bound for A. Also, if q>√3 then α≤2q, because every such 2q is an upper bound for A (and α is the smallest). We want to improve the ≤ to <. For this we need another important property of R: between any two real numbers there is a rational number. (We will prove this later.)

We use that property as follows: if p<radic;3 then there is a rational number r such that p<r<√3. For that r we have 2p<2r≤α and so 2p<√3. In exactly the same way you can show that α<2q whenever q>√3.

At most one

Now we must show that only α meets our requirements. We do that by showing that the diameter of the set of suitable numbers is equal to 0; and that means that only one number will fit in the set.

Take two rational numbers p and q in the interval (1,2) with p<√3<q. The difference 2q-2p is equal to 2p(2q-p-1). On the interval (0,1) we have 2r≤1+r (we will show this later). We can use this to bound 2q-2p:

The last inequality is because p<2. Now we can show that the diameter of the set of suitable numbers is equal to 0.

To see that the diameter is less than 10-6 we calculate the first seven digits of √3 after the decimal point. Then we see that p<√3<q, where p=1.7320508$ and q=1.7320509. We have q-p=10-7 so that

By doing this for ever better approximations of √3 we find that the diameter is smaller than every positive number that we can specify. The diameter is therefore equal to 0.

Properties of 2x

In exactly the same way as for √3 we can determine what 2x is for every real number x that is not rational: 2x is the unique number y with the property that 2p<y<2q for all rational numbers p and q that satisfy p<x<q.

The function that we construct in this way has all properties that we may expect of an exponential function.

Exercise Verify that 2x×2y=2x+y for all real numbers x and y.

We can also prove that 2x<2y when x<y (we only know this if one of x and y is rational). First take a rational number p with x<p<y; then we know 2x<2p<2y

Many rational numbers

Take two real numbers x and y with x<y. Then the difference y-x is positive., hence there is a natural number n such that 1/n<y-x. Then we also have 1<nx-ny; that means there is a whole number m between nx and ny. But then we see that x<m/n<y. So there is a rational number between x and y.

An inequality

We still need to show that 2r<1+r when r is an rational number in the interval (0,1).

We use the AGM-inequality again.

Write r=k/n. And apply the AGM-inequality

to the following n numbers: x1=…=xk=2 and xk+1=…=xn=1. We get

or 2k/n≤1+k/n.

Other bases

For every number a>1 we can define the function ax in exactly the same way as for 2. The proof that there is exactly one possibility for ax when x is not rational needs a few modifications.

If you replace every 2 by an a in the section on the inequality then you will get

Simplification of the right-hand side yields

When we determine a√3 we take p<q in the interval (1,2) and then we get

and this helps in showing that there is only one number that is suitable to be a√3.

If 0<a<1 we define ax via 1/a: ax=1/(1/a)x.

[wiskwa-en]

Advanced Power Taking, I

This is a translation of an article that appeared in the January 2006 issue of Pythagoras.

What is 2√3 exactly? In this post we shall give an exact definition of the exponential function 2x for all real numbers x. We also look at other bases for exponential functions.

The last two times we saw why n-th roots exist and how you can approximate then quite efficiently. Now we see how we take powers; that is not completely straightforward. We shall see a proper definition of 2x for all every number x.

To begin: for natural numbers the meaning of 2n is clear: 2n is usually introduced as a convenient abbreviation for

For arbitrary whole numbers we should be more careful: we cannot just say that

and

because those two definitions do not really mean anything. The proper definition of 20, 2-1, 2-2 … comes from the desire to preserve a very useful property of 2n: we always have 2m×2n=2m+n. For m=0 this leads to 20×2n=2n and that means that we should have 20=1 as the only correct possibility. Because 1-1=0 it follows that 2-1 should be chosen so that 21×2-1=1 and so 2-1=½. And likewise 2-2=¼, …, 2-10=1/210=1/1024, …

Exercise. Verify that with this definition the property 2m×2n=2m+n holds for all integers m and n.

Fractional exponents

What should 2q be when q is a rational number, that is, when it can be written as n/d with whole numbers n and d (d≠0). If q=½ then the preservation of the property dictates via 2½×2½ =21=2 that 2½=√2. Likewise 2⅓=∛2, … 21/10should be the thenth root of 2, and so on. So: 21/d will be the dth root of 2 and then 2n/d=(21/d)n.

Exercise You can write a rational number as a fraction in more than one way, for example ½=2/4=3/6. We have made separate definitions of 2½, 22/4 and 23/6. Verify that those three values are equal.

Exercise Show: if n/d=k/l then (21/d)n=(21/l)k

Exercise Now prove: if p and q are rational numbers then 2p×2q=2p+q.

Next time we will deal with irrational exponents.

[wiskwa-en]

Advanced root extraction, II

This is a translation of an article that appeared in the November 2005 issue of Pythagoras.

Last time we showed why ∛2 exists. This time we see how we can approximate ∛2 efficiently.

An approximating sequence for √2

To find a sequence of approximations of √2 you start with x0=2 and, successively, once you have xi calculate a new approximation xi+1, as follows.

So, x1=3/2, x2=½(3/2+4/3)=17/12, and so on. The sequence that we get in this way is decreasing and every term is larger than √2. To see this we need the AGM-inequality, first for two distinct numbers a and b:

We have x0>√2 to begin with and whenever xi>√2 we have xi>2/xi and so

(the average is smaller than the larger number) and by the AGM-inequality we get xi+1>√2. These approximations converge quite rapidly to √2; if you rewrite xi+1-√2 then you ge

and this is equal to

(just expand the square). And because xi>1 we find that

This means that the number of correct decimals roughly doubles each time. To begin x0-√2<0.6 and so x1-√2<0.62/2=0.18, x2-√2<0.182/2=0.0162, and then x3-√2<000013122, and so on.

In general, to create a sequence of approximations of √a start with x0=a and repeat the step

A sequence for ∛2

In a similar fashion as above we can create a sequence of approximations for ∛2. We star with x0=2 and each time we create a new approximation from xi as follows

Again we find a decreasing sequence with xi>∛2 for all i. You can show this using the three-number version of the AGM-inequality:

Put a=b=xi and c=2/(xi)2. The product of the numbers is equal to 2 and the average is smaller than the largest number, which is xi.

Just like in the case of √2 this sequence converges quite rapidly, with a bit of work you can verify that

Because every xi lies between 1 and 2 you derive that

This means that also here the number of correct decimals will, roughly, double in each step.

The n-th root of 2

For other n-th roots you can create similar sequences. Star with x0=2 and keep repeating

The resulting sequence will converge to the n-th root of 2.

[wiskwa-en]

Advanced Root Extraction, I

This is a translation of an article that appeared in the September 2005 issue of Pythagoras.

What is ∛2, really? What is its definition? How do you know it exists?

If someone asks you what √2 is, what do you say? Not `the square root of 2', because that is saying the same thing but then in words. The correct answer is: it is an abbreviation of `that positive number whose square is equal to 2'. The next question might be about the value of √2. And then you will have to explain that √2 can not be expressed as a fraction and that √2 is really not more than an abbreviation. Then you get a tricky question: how do you know that it exists? Fortunately you can use a bit of geometry to point out the position of √2 on the number line.

Just make square whose sides have length 1 its diagonals then have length √2.

What is ∛2?

The question about ∛2 has a clear answer: `the positive number whose third power is equal to 2'. Does that number exist as well? Can we point out where it is on the number line? That depends of course on what you mean by `pointing out', but it is not as easily done as for √2. Not only is ∛2, like √2, not expressible as a fraction but there is even no geometric construction with ruler and compasses that will give a line segment of length ∛2.

We can of course try to point out where ∛2 is approximately. If you set a calculator to work you will soon discover that 1.23<2<1.33, so that ∛2 lies in the interval (1.2,1.3). If you keep going you will find 1.253<2<1.263, … 1.25598921043<2<1.25598921053, and so ∛2 lies in the interval (1.2559892104,1.2559892105). If we keep going we shall make ever smaller intervals that should contain ∛2. And in this way we seem to find ever more digits in the decimal expansion of ∛2, but at no point do we actually have ∛2 itself and it is not certain whether ∛2 actually exists. After all it could be that in between all those approximations there is a gap in the number line and that we have been calculating with something that is not there.

Fortunately that is not the case. There are no gaps (or holes) in the number line and that is a property that makes basically all of Mathematical Analysis possible. Thanks to that property we can show that ∛2 exists. The beauty of the property and the proof is that you can show in the same way that all nth roots of 2 exist. That makes the property so very important: it can be used to prove the existence of very many numbers all at once.

A fundamental property

The mathematically precise formulation of "the number line has no holes" is "the number line is complete".

To formulate what completeness means we need the concept of upper bound.

Suppose A is a set of numbers; a number x is an upper bound of A if a≤x holds for all a in A. For example 1000 is an upper bound of the interval [0,1) and 2 is an upper bound of {x:x2<2}. Of course 1000 is a very crude upper bound of [0,1), there are better ones, 10 is also an upper bound, as is 1. We cannot go below 1 of course: 1 is the least upper bound of [0,1).

When you draw (or write down) more examples of sets of numbers you will see that whenever there is an upper bound there is always also a least upper bound. This property holds for all sets (even if their description is not so simple).

Theorem Every nonempty set of numbers that has an upper bound also has a least upper bound.

A proof of this fundamental property is not that easy; you can give one if you know exactly how the real numbers are made. We save that for a later post.

Now we will show how you can use completeness to prove the existence of ∛2.

The existence of ∛2

Consider the set A={x:x≥0 and x3<2}. That set is not empty because 0 and 1 belong to A; the set has an upper bound, 2 for example. Now we can conclude that there is a number α that is the least upper bound of A, so x≤α for all x&in;A (as α is an upper bound), and if $β<&alpha then there is an x&in;A such that x>β (as α is the smallest upper bound). We shall prove α3=2 and hence that we established the existence of ∛2.

We need a formula: for all numbers x and y we have

y3-x3=(y-x)(y2+xy+x2)

You can verify this by expanding the right-hand side. Using this formula we can find everything we need.

To begin: if 0≤x<y then x3<y3. This follows because y2+xy+x2 is positive. From this we deduce that once we have shown that α3=2 we know that there is no other number with that property.

Next: if 0<x<y<2 then

y3-x3<(y-x)(4+4+4)=12(y-x)

In particular: if x&in;A then

α3<x3+12(α-x)<2+12(α-x)

Because we can make α-x as small as we please it follows that α3≤2.

Third: if α<y<2 then

alpha3>y3-12(y-α)≥2-12(y-α)

(because y is not in A we have y3≥2). Again we can make y-α as small as we please and deduce that α3≥2.

Conclusion: α3=2.

Remarks

In the same way we can show that every nth root of 2 exists, for every n, as the least upper bound of the set

An={x:x≥0 and xn<2}

There is nothing special about 2 of course; we can use the above arguments to prove the existence of the nth root of a for every positive number a and every natural number n.

Next time we will discuss an efficient way of making approximations of those nth roots.

[wiskwa-en]

Ramsey’s Theorem, II

This is part two of a translation of an article that appeared in the April 2005 issue of Pythagoras.

In this part we state and prove the finite version of Ramsey's theorem for pairs.

Ramsey numbers

Last time we investigated how large a party should bein order for there to be groups of people who all do or who all don not know each other. Ramsey's theorem states that you can always find large enough groups provided the party has enough guests.

Ramsey's theorem for pairs. For every two natural numbers k and l there is a natural number N such that at every party with N guests there will be a group of k people that all know each other or a group of l people that all do not know each other.

The smallest number that works for k and l will be written R(k,l); the R(k,l) are called Ramsey numbers, after the logician Frank Ramsey who proved in 1929 that these numbers actually exist. The theorem is often presented as one about graphs: given natural numbers k and l there is a natural number N such that no matter how we color the lines connecting N points green and red there will be k points such that all lines between these are green or l points with all lines between them red.

The story about the party with six people shows that R(3,3)≤6 and the special party with five guests shows that R(3,3)&gr;5 and so R(3,3)=6.

To show that the numbers R(k,l) actually exist we shall derive upper bounds for them. Before we do that we make two simple observations.

First: by interchanging `knowing' and `not knowing' (or green and red) we see that R(k,l)=R(l,k). Second: R(k,2)=k, because at a party with k guests everyone knows each other or two people do not.

The argument that we used to show R(3,3)≤6 can be used to show the following inequality:

This works as follows: suppose you have R(k,l-1)+R(k-1,l) people at your party. Pick one guest and divide the rest into two groups: d people that she does know and n people that she does not know. Then we have, of course

We cannot have both d<R(k-1,l) and n<R(k,l-1) because then we would have d+n≤R(k,l-1)+R(k-1,l)-2. So, we have two possible cases.

Case 1 d≥R(k-1,l). Then there will be among those d people either l people that all do not know each other (and we are done) or there are k-1 people that all do know each other and together with the special guest they form a group of k people as desired.

Case 2 n≥R(k,l-1). You can deal with this case yourself.

If you look back at our first argument then you will see that it proves R(3,3)≤R(3,2)+R(2,3). After that we used the exact same argument to prove that R(3,4)≤R(3,3)+R(2,4)≤6+4=10. Then we used a more detailed argument to show that, in fact R(3,4)≤9 and then, by an example, that R(3,4)>8 and hence R(3,4)=9.

We ended the last post with an exercise to find an upper bound for R(4,4) and maybe you had already discovered that R(4,4)≤R(4,3)+R(3,4)=9+9=18.

Exercise. Find an upper bound for R(5,5). How many steps would it take to find an upper bound for R(10,10)?

Exercise. Draw a regular 17-gon, number the vertices 1 through 17 and color the line connecting i and j red if j-i is equal to 1, 2, 4, 8, 9, 13,15, or 16 and green otherwise, see the picture below. Now verify carefully that there is no set of four points with all connecting lines of the same color. Conclusion: R(4,4)=18.

A general formula

You may have noticed that our inequality looks a bit like a well-known equality for binomial coefficients

As we just saw we have R(k,2)=k and we can write that as

The last form makes the 2 visible. Using the principle of mathematical induction you can extend this to the following theorem:

Theorem. For every k and l the following inequality holds.

This shows that the numbers R(k,l) exist and it gives us an idea of their size.

Small improvements

The inequality in the theorem is not sharp. We saw that with R(3,4) and R(4,4). The theorem gives

but we already know that R(3,4)=9 and R(4,4)=18. The more precise argument that gave us R(3,4)≤9 can be used to prove the following: if R(k-1,l) and R(k,l-1) are both even then

We need just one person with d≥R(k-1,l) or n≥R(k,l-1); if that never happens then always d=R(k-1,l)-1 and n=R(k,l-1)-1 and that would, again, lead to an odd number that should be even.

The exact value of R(k,l) is known for very few pairs (k,l). People are still looking for better estimates, from below and from above). At this address you can find a table and further references. You will see that R(5,5) is still not known; what is known is 43≤R(5,5)≤49.

[wiskwa-en]

Ramsey’s Theorem, I

This is part one of a translation of an article that appeared in the April 2005 issue of Pythagoras.

When you distribute very many things over very few boxes then at least one box will get quite full. Many results in mathematics rest on this simple observation; Ramsey’s theorem is one of the most beautiful examples of this.

If you write down five different natural numbers then you know for sure that at least three will have parity (the same remainder upon division by 2). In other words if you only use the property `odd or even’ to distinguish numbers then in a set of five there will be three indistinguishable numbers.

You make many variations on this theme: put 367 people together and you know that there will be two that share a birthday (remember leap years). If you pick thirteen (real) numbers from the interval (-½π,½π) then two will differ by less than π/12. You can formulate a general theorem.

Theorem. If m and n be natural numbers and if you distribute n×m+1 things over m boxes then at least one box contains at least n+m things.

Ramsey’s theorem, which we discuss in this post, says that things like this will happen always: if you write down a finite number of properties then given a natural number n you can always find a natural number N such that in every group of N people you will find n people that cannot be distinguished using these properties. The properties that Ramsey’s theorem speaks about can also apply to pairs, triples and so on. In this post we will deal with pairs only.

Do you know each other?

At a party you can determine of every two guests whether they know each other or not. If there are six people present then you can make a group of three such that all~three know each other or such that all three do not know each other. Here is how. Pick one guest and divide the five others into two groups: those she knows and those she does not know. As we saw above if you divide five things into two groups one group has at least three members. So, for example, our one guest knows three other people. If none of the three know each other then we are done. If two of these know each other then they with the one guest form a group of three where everybody know each other. See the pictures below, where a green line means `know each other’ and a red line means `do not know each other’; the dashed lines represent the two cases that we had to consider.

Five guests only. With just five guests this argument will not work and, indeed, you can create a situation where no group of three as desired can be found.

Again green means `knowing’ and red means `not knowing’; there is no triangle with all sides of the same color

On to four

The next logical step would be to see how large the party should be in order to get a `homogeneous’ group of four people; homogeneous means that all pairs have the same property. We shall do this but it turns out to be easier to look at non-symmetric situations too. Therefore we first look for a meeting where there are either four people that know each other or three that do not know each other.

Four that know each other or three that do not. We follows the earlier strategy: set aside one guest and divide the rest of the guests into two groups, those she knows and those she does not know. In the following, favorable, situations we can deduce that there are four people that all know each other or three that do not.

Situation 1: she knows six people at the party. This gives us two cases:

three of these do not know each other and we are done

three of these do know each other and with our separate guest this gives a group of four that all know each other

Situation 2: there are four people that she does not know. Again we have two cases:

all four know each other, and we are done

two of these do not know each other and with our separate guest this gives a group of three that do not know each other

From this we see that it suffices to have nine other guests; then one of the favorable situations must present itself. This shows that ten guests is enough.

Nine guests is enough. But even at party with nine guests is large enough. The point is that we need just one guest for whom one of the good situations occurs (with ten guests we get that for everybody). For every guest there are eight “others’ and if there is never a favorable situation then everybody knows exactly five people and does not know exactly three. Draw a line between every pair of guests that knows each other. This makes everybody an end point of five lines, there are nine people and hence 45 end points in total. But that is impossible: every line has two end points, so there must be an even number of end points.

Eight is not enough. Look at the following picture.

As before green means `knowing’ and red means `not knowing’. Number the points 1 through 8, anti-clockwise. If you look closely you will see that there is a green line between i and j if the difference j-i is equal to 2, 3, 5, or 6; it is red if the difference is 1, 4, or 7. There is no red triangle, for let i

Four that know each other or four that do not. With what we learned so far it is not very difficult to determine an N such that at every party with N guests there will be four that all know each other of that all do not know each other.

Exercise. Determine an N that suffices for the four-four situation. Is your N the smallest possible one?

Next time we shall use the method of setting one guest aside to tackle the general problem: with many people can we be sure that there are k people that know each other or l people that do not know each other?

[wiskwa-en]

A rope around the Earth, II

This is part two of a translation of an article that appeared in the November 2004 issue of Pythagoras. This article also appears in Half a Century of Pythagoras, an anthology of articles from the magazine published by the MAA.

We put a rope around the earth, make it a bit longer and pull it up so that it becomes tight again. How high do we have to pull it? Can we express the height in terms of the length of the extra piece of rope?

In yesterday's post we saw that if you take a rope that is one meter longer than the circumference of the Earth and pull it up at the North pole (assuming the rope goes around the Earth along the 0- and 180-meridians) it will go up a 121 meters and a bit before it is taut again. In this part we try to find a good (and quick) formula for that height in terms of the length of the extra piece of rope.

An efficient approximation

Let us look at yesterday's picture once more

It lead us to two pieces of information: after applying Pythagoras' theorem we found

which we could also write as

From the picture we read off that

or also

When we combine this we can also write

This expresses h in terms of α but we would like to express h in terms of ε. That can only be done implicitly: α is a solution of the equation

and there is no `nice' formula for that solution.

However, our angle α is very small. We have seen that in that case the expression α+⅓α3 gives a very good approximation of tanα. If we insert this in our equation then we get

In addition the value of tanα itself is very small too. For very small x we have √(1+x)≈1+½x; this helps us to simplify the formula for h to an approximation

Next we expand the square to get

Putting in our numbers again gives us Rα2=242.8 m, Rα4=0.009 m and Rα6=3.5×10-7 m. For all practical purposes we can discard the fourth and sixth powers to get the following approximation of h:

A few moments ago we found

if we plug that in we get

If we put in the value of R then we get the following approximation of h

The beauty is that this does not give an essentially different value from the one we found in the beginning: putting ε=0.5 the formula will give us h≈121.4 m as well.

Exercise Use ε=0.005 our formula. How much does the value of h differ from that in yesterday's exercise?

Exercise Investigate how accurate the approximation √(1+x)≈1+½x is. For example, compare (1+½x)2 with 1+x; for what x is the difference small enough to be discarded? Was the use of of the approximation in our example justified?

Remark We can isolate ε in our formula:

this gives important qualitative information: h is approximately equal to a constant times the two-third power of ε Readers familiar with error terms for Taylor polynomials may enjoy working out what the order of the error is in this approximation.