#intermediate value theorem

[spaciebabie]

they're what this post is abt btw

got my penis sucked last night heh . it hurt so bad i scrumpt like tom and jerry

[skyes-messy-desk]

I mayyy have slept until noon today despite having several alarms set for much earlier. Oops! But guess what guys. I'm so excited, I got tickets to see Pierce the Veil this summer!!! The thought of going to that concert is literally keeping me going right now.

Anyways, here's today's agenda:

Bio post-test for extra credit

Calc practice problems (specifically limits and intermediate value theorem)

Chem practice problems (specifically thermochemistry and orbitals)

[notonlymaths]

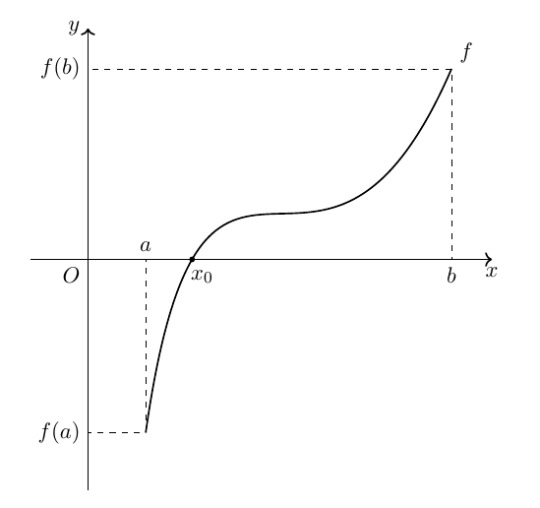
Okay, so, the Intermediate Value Theorem (IVT) clearly states that if you start from point (a,f(a)), below the x-axis, and move towards (b,f(b)) above the x-axis without lifting your pen up, you have to cross the x-axis at some point; (x_0,0) here. But, isn't that too obvious to be a theorem?

Can you see the hidden implication here for the foundations of mathematics?

[darrenpeace-shitpost]

Yesterday I passed my mathematical analysis colloquium, and now I have a bit more free time and less stress! I’m back

My notes look like I’m insane and have an extremely bad handwriting

(It’s the intermediate value theorem’s proof)

[positivelyapunovexponent-good]

okay so

tested positive for COVID a couple of hours ago. Running low grade (100.4-100.6 deg F) fever that just won’t break. Every single time time I tried to fall asleep for the past four hours I resumed the exact same fever dream about trying to prove the Heine Borel theorem but about my brain?

or rather. Specifically the preparatory theorem for Heine Borel in Rudin proving any closed bounded k cell comprised of the Cartesian product {[a_i, b_i]}\for all i \in [k] is compact in \mathbb{R}^k by supposing not and then deriving a contradiction by partitioning the k cell into the union of 2^{nk} cartesian products of intervals of length {(b_i- a_i)/2^n} \forall n \in \mathbb{Z}_+, supposing there is an open cover G of the k cell that does not have a finite subcover on a nested sequence these intervals chosen at each step n, and then showing by intermediate value theorem that nested intersection of those intervals contain a point x of the k cell so there is a neighborhood in G containing x and all but a finite of the intervals which means there is in fact a finite subcover wonders! Yeah that one

so the dream is like. Imagine your brain is a k cell in R^k packed full of an uncountable number of ittty bitty neurons but they are SICK and DYING of fever so you need to come up with an open cover of your brain that isolates out the sick neurons in their own quarantine open sets so they don’t infect the other neurons but you need to show any such open cover has a finite subcover because otherwise I guess you chop the neurons too thin when partitioning them? And that’s bad because it means your brain breaks? I dunno that part of the dream doesn’t make any sense but it feels very urgent.

anyways. So I keep waking up in a cold sweat feeling my dream proof is somehow wrong or incomplete. And then I fall back asleep and the dream repeats. So now it’s 6AM and I’ve had to scrounge up my old pdf of Principles of Mathematical Analysis by Rudin and make sure I had that proof down cold. And I’m actually proud of how well I remembered it even when in a fever addled dream state. So I guess I really do know the Heine Borel theorem which is nice!!! I just hope that is sufficient to satisfy the Plague Brain

[transgenderer]

What is infinity?

i know countable infinity. just keep counting. cardinality of the natural numbers. uncountable infinity...well. idk about all that. but you need it for intermediate value theorem and im a big fan of that. "cardinality of the set that makes intermediate value theorem true". not a fan of any of the other infinities tbh. omega. omega^2. etc. the ordinal numbers kinda suck. nongeometric!

[kittehxx]

since such a middle point does not exist, we conclude by the intermediate value theorem that the size of the deal is discontinuous with respect to time

First you procrastinate on the task because it is not a big enough deal to get done urgently. Then you procrastinate on the task because it has become such a big deal that doing it is overwhelming. You would think that this implies a middle point where it is just big enough of a deal to get done easily, however the inherent perversity of the universe's causal geometry prevents this

[tidaltinkerer]

Pure Mathematics. Topic Numerical Techniques.

Since I have a test on Monday I thought I would use this blog for its intended purpose.

When the normal techniques do not work, we use numerical Techniques to find the root of a function. The normal techniques are factorization, completing the square, and using the quadratic formula x= -b +- square root (b2-4ac )  /2a. 

    Firstly, we NEED to establish that there is a root, to do so we use the intermediate value theorem (IMVT). The formal definition of the IMVT is that

IF y=f(x) is a continuous function in the interval a<x<b and if “k” is a number which lies in between f(a)<k<f(b) or f(b)<k<f(a) then there exists at least one number “c” such that “c” lies between a<c<b and f(c)=k. 

BUT there is no need to commit the definition to memory 

Going back to establishing the root. 

Eg. Show that x^2 -3x - 1 = 0 has a root in [3,4]      

         The [3,4] in this case means interval,  3 < root < 4 or the root lies in between 3 and 4.

         For a root to exist there MUST be a change in sign either (-ve to +ve) or (+ve to -ve).

f(3) = 3^2 - 3(3) -1 

      = -1

f(4) = 4^2 - 3(4) - 1

      = 3

          What I just did is called substitution. I replaced the value of x with the values in the given interval.  

    Now we write a STATEMENT, the change in sign indicates that there is a root, and a statement is needed.

Since f(x) is a continuous function in [3,4] and f(3) x f(4) <0 then by IMVT there exits a root such that 3 <root< 4

3< root< 4 This means that ← the root lies in between the interval                

f(3) x f(4) <0 this means multiplied it produces a negative value which is less than 0  

This needs to be memorised. 

There are four methods in this topic:

Interval bisection

Liner Interpolation

Newton-Raphson

and

Fixed Pt Iteration 

In this post, I'll be covering Interval Bisection and Liner Interpolation.

Interval Bisection

First Prove that there is a root

f(x) ; x^2 - 4x + 1 = 0,  [3,4]

f(3) = (3)^2 - 4(3) + 1

      = -2

f(4) = 1

Since f(x) is a continuous function in [3,4] and f(3) x f(4) <0 then by IMVT there exists a root such that 3 < root < 4. 

Now using the interval bisection method

WE FIND THE MIDPOINT

3+4/2 = 7/2 = 3.5

Consider f(3.5) = (3.5)2 - 4(3.5) +1 = 0

f(3.5)= -0.75 

Now we change the interval 

Since f(3.5) x f(4) <0

Then 3.5 < root < 4   or [3.5, 4]

Keep in mind that the root EXISTS where there is a change of sign 

3.5 +4/2 = 3.75

Consider f(3.75)= 0.0625

Since f(3.5) x f(3.75) < 0

    Then 3.5 < root < 3.75   or [3.5, 3.75]

3.75 + 3.5 /2  = 3.625

Consider f(3.625) = -0.359

Since f(3.625) x f( 3.75)

Then 3.625 < root < 3.75

After a few more rounds you should get 

3.719 < root < 3.734    identical to 1 decimal place

As you can see this method can be lengthy

A question you might have is How do you know when to stop?

Well 2 ways:

When they are identical to the asked decimal places

eg. 3.7 < root < 3.7 which is identical to 1 decimal places

or after how many iterations they ask you for.

eg. Do interval bisection 3 times. With reference to the example we worked out above the answer here would be 3.625 < root < 3.75

 LINEAR INTERPOLATION 

 There are two proofs included in this method that I’ll attach a picture of below. You must memorise these proofs

In this method, we assign the interval value as either a or b. A is normally used for the smaller interval value and b for the larger interval value. 

We then find f(a) and f(b) and then substitute into any one of the formulas in the above proof.  An example of this is the picture below

There was no need to continue since 0.2 < root < 0.2

As stated we only need to put the statement: since f(a) x f(b)< 0, a< root< b if we are doing another interpolation which is why there is an absence of that statement after working out x2.

Again we stop either when the interval is identical to the stated decimal points or after how many iterations.

Hope you found this helpful, I'll post the second part... sometime😅 but for now I have to revise those other two methods for my test tomorrow.

[jonathankatwhatever]

I’m amazed at the extent to which there is work proving construction without seeing that this means it is constructed. An example is the intermediate value theorem. If you draw a line from a to b, then it will be continuous, and that means it will construct each point you can identify along the line. So the hand pushing the pencil, in the tangible or abstract sense, connects to that concept, to that theorem if you prefer. This is another version of the availability issue, that for a pattern to repeat, there must be a mechanism by which that pattern is available to repeat. That means the availability is external and internal and that there is a matching process which relates those. In other words, it’s like there’s a library of code which can be run and it gets very specific because it is contextual.

What then is the operation of context? We spend a lot of time talking about operations and we know the answer is in the construction of gs. But what are the mechanics of context so it shifts? I’m seeing that as a series of choices, left and right, etc., meaning pairs and thus K’ing and Q’ing, where the Q is the image of a gs with an Attachment which aligns to the K’ing. The pair completes when you overlay the Q’s over the facing K’s. Or other way round.

In most cases, the choices are complicated because there are so many pairs. This is why dance training works; it constructs forms which act like when I stabilize myself in a deep squat so the cat can circle to a fixed attachment, meaning that enables choices to that structure. In dance or any such training, this structure opens up the ability to move more as intended for that discipline. I remember that from Latin class: discipuli, the discipline of the student.

That discipline is a form is a method is an approach which acts as an Attachment, meaning it acts as a doorway or window if you prefer into the movements within the discipline being studied by the discipuli.

I’m having trouble concentrating again.

The operation of context then becomes a pair choice in which the pair consists of contexts themselves.

[ego-tempestas]

Kid named intermediate value theorem

The masculine connotation of a bow tie and the feminine connotation of a bow on the top of the head implies a nonbinary bow style placed directly over the nose

[thelemmallama]

some random thoughts on complicity

wrt "you're either part of the problem or part of the solution":

maybe less about inaction and more about beliefs

inaction (or at least a comfortable awareness of the facts of the situation) implies the belief that 'there is no problem', which is directly antagonistic to the belief 'there is a problem'. (whereas a passive rock doesn't rub us the wrong way in the same manner because rocks don't have beliefs, so we don't deduce that the rocks believes 'there is no problem')

the real middle ground, 'there may or may not be a problem', does not imply inaction. it implies asking questions, or retreating in more of a 'sorry, but i don't have the time or energy to learn more about this problem' kind of way; which usually implies a bit of discomfort (if you're 50% sure you left the stove on, you probably won't be totally comfortable just continuing your shopping trip and taking your time getting home) and also not staying around to gawk (because that at least implies you have the time to learn more)

(older)

what is 'complicity', really?/"true bystanders are perfectly fine, actually"

complicity is a valid critique

but 'you can't stay neutral on a moving train' is not entirely correct

there's a spectrum of actions between helping one side and hindering them; at some point one must necessarily cross over some notion of 'neutral' (saku: [explains this], dolly: right, the intermediate value theorem)

the real observation here is the neutral action has no relation to the 'default'/'lowest effort' action. the 'standard/default' action is almost never truly 'do nothing'.

neutrality exists, in some meaningful sense, but it's not a simple or fixed concept. being truly neutral isn't a matter of 'doing nothing', as our notion of 'nothing' is biased towards what we're used to as the default. [white canvas vs blue canvas; we might say the white canvas is a 'blank' canvas, but someone wo's used to blue paper would disagree]

a person existing in their most low-effort state is different from a rock existing in their most low-effort state. rocks are not trained and habituated into going along with social norms.

imagine if a person truly acted like a rock. they would be considered a very abnormal person. plus it actully costs us more effort to stay completely still, than to let social and biological pressures animate us

being complicit is more like being a rock and letting someone pick you up and throw you at someone's face

but you are not hurting anyone by simply existing as a rock lying on the ground

then all we have the obligation to do, is to self-modify such that we are useless as weapons against others. if the rock become a cushion, it matters far less if someone picked it up and threw it at someone else. they likely wouldn't even bother.

[quantum-friend-theory]

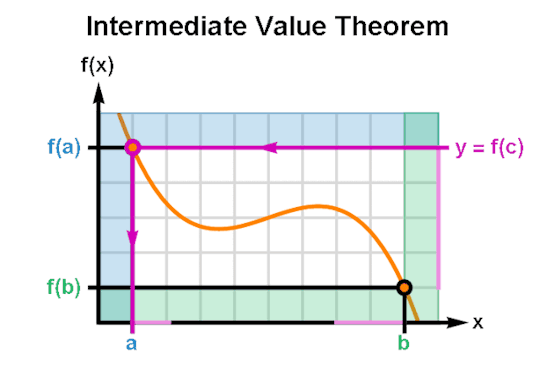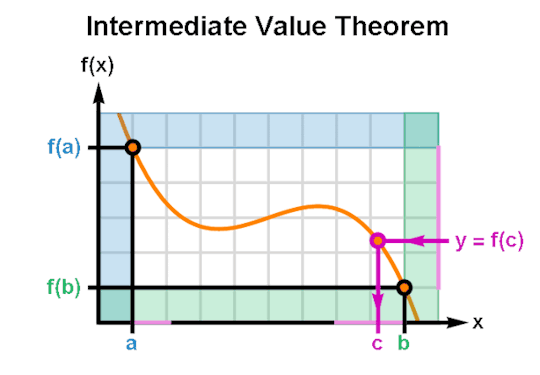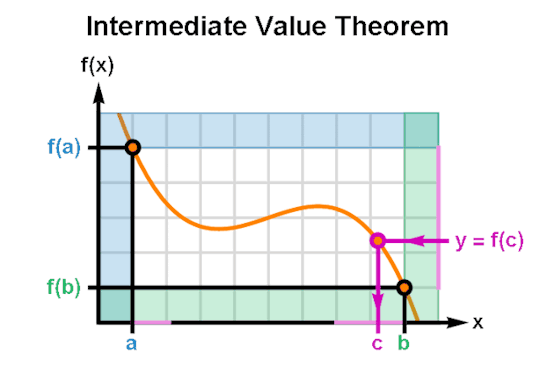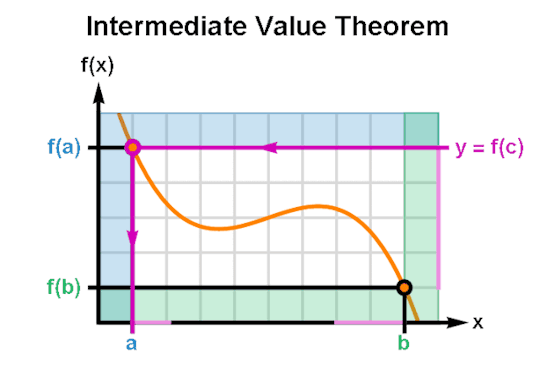
The Intermediate Value Theorem guarantees that for every real number "y" between two outputs of a real continuous function f(x) there exists at least one value "c" between the corresponding inputs such that y = f(x) when x = c.

(GIF Description: The graph of a function f(x) as it ranges from x = a to x = b. Per frame, an output value y between f(a) and f(b) is shown to intersect the curve f(x) for some x = c. As the GIF animates, y sweeps across the range of f(x) and indicates a value of c for every y.)

[maybeasunflower]

The Intermediate Value Theorem also only applies to functions that continuous in domain (or subsets thereof). As people are discrete, not smeared out continuously over a landscape, the IVT does not apply here.

[revelatorytruths]

Intermediate Notes -- Directory

Intermediate Notes — Directory

How Human Beings are Created and Why? What is Thought?  What is Personality? The Components of the Eternal Evolution of You! God’s Thought Controls all Creation! The Eternal Reason You are Here! The Eternal Reason All Exists! Life after Death! God Delegates Everything! So What is The True Meaning of Life? How to Survive Death! The [Mind] … Location of You! Revelatory Sayings! Jesus Teaches ……

[tutor-eye]

Get AP math calculus tutor online. Online tutoring services 24x7. Study math from qualified tutors at TutorEye.