factomaniac

[factomaniac]

Math Madness #3: The Pythagorean Theorem Wasn’t Discovered by Pythagoras, and Other Facts About

a² + b² = c²

Thursday, 13 June 2024, Chicagoland, IL

Mesopotamian mathematics historians have established that, despite the name it is known by today, the Pythagorean Theorem was widely known in the Old Babylonian Empire existing from the 20th to the 16th Centuries BC, over 1,000 years before Pythagoras of Samos, the theorem’s namesake, was even born around the middle of the 6th Century BC in either the Greek island of Samos, or the city of Tyre in present-day Lebanon (Wikipedia “Pythogorean Theorem” 2024, Neugebauer 1969, Friberg 1981, Hørup 1998, Robson 2008, Wikipedia “Pythagoras” 2024, Porphyry 2014).

The Pythagorean Theorem asserts that in any right triangle, a triangle containing one right angle (an angle of 90°–ninety degrees–or π/2 radians), the area of a square where each side is the length of the triangle’s hypotenuse (the side of the triangle opposite the right angle) is equal to the sum of the areas of two squares where each side of each square is the length of each of the other sides of the triangle, which are perpendicular to one another.

By the way, the word hypotenuse comes from French, by way of Latin hypotenusa, ultimately originating from the Ancient Greek ἡ ὑποτείνουσα (“hē hypoteínousa”), meaning “the [side] stretched below [the right angle]” because, in Ancient Greek times, right triangles tended to be drawn with the right angle pointing upward, therefore, the hypotenuse appeared to be stretched below the other two sides forming the right angle (Wikipedia “Hypotenuse” 2024, Liddle, Scott, Jones 1940/Perseus Project 2024, Online Etymology Dictionary “Hypotenuse” etymonline.com 2024).

Although typically this theorem is typically stated as something like “the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides,” and written algebraically as a² + b² = c² today, in ancient times, it was originally construed geometrically with actual squares on the sides of the right triangle. Remarkably, thousands of geometric and algebraic proofs of the Pythagorean Theorem exist. One very simple modern geometric proof is below.

Besides serving visually as a proof of the Pythagorean Theorem, the above illustration also makes a good jumping off point for an algebraic proof of it as well. Referring to the second frame of the illustration with the c² square in the center, notice that the sides of the entire frame each measure a + b. Therefore, its area can be found by squaring this expression: (a + b)². Also notice how the area of the frame can be found by adding the area of the c² square itself to the areas of each of the four triangles, ½ab: c² + 4(½ab). The Pythagorean Theorem then pops out just by writing an equation that sets these two expressions as equal to one another.

(a + b)² = c² + 4(½ ab) → a² + 2ab + b² = c² + 2ab → a² + b² = c²

By the way, the equation of the Pythagorean Theorem can also be rearranged to find the length of one of the sides of a right triangle while knowing the length of the other two sides:

∵ a² + b² = c², c = √(a² + b²), a = √(c² - b²), b = √(c² - a²) (∵ symbolizes "because" and √(x) is "the square root of x").

Originally, Euclid proved this theorem by taking a right triangle with the right angle pointed upward and the hypotenuse as the base at the bottom and then, as I mentioned above, making squares off of all three sides of the triangle whose sides are the length of the respective triangle sides they are formed from.

Although I’m presenting what is essentially Euclid’s proof of the Pythagorean Theorem, I’m going to put my own spin on it in that I’m going to refer to the points, lines, and shapes in a way very different from how it is done in classical geometry. Because one thing I recall that I found confusing when learning classical geometry in primary and secondary school was the reference to shapes by the points that form their corners, such as referring to a shape as Triangle ABC—or worse △ABC—because it contains the points A, B, and C, or saying that one shape is congruent to another because they contain proportional sides that meet at points forming the same angles. I’ve always found the semantics and vocabulary of classical geometry baffling compared to, say, algebra or even calculus. Therefore, points will have miniscule Greek letters, the lengths of lines will be referred to using miniscule Roman letters, and the shapes are depicted with Roman numerals. (Please note that I will occasionally use traditional notation as well as my own notation in order to avoid confusion.)

First, we have Triangle I in dark grey (traditionally defined by points ϙ [qoppa, pronounced “COPE-ah”, an archaic Greek letter now only used as a numeral], α, and β, or symbolically as △ϙαβ) with sides of lengths a, b, and c, a is the length of the side of the triangle on the right side of the right angle, b is the length of the side on the right angle’s left side, and c is the length of the hypotenuse, in the style of the ancient Greeks, on the bottom of the triangle forming its base. Next, there are the squares in white (Squares II [□ϙηιβ], III [□αφγϙ], and IV [□βαδε]—see the uniting brace on the bottom of Square IV) formed from each of Triangle I’s sides, all of whose sides, by definition, are all the same exact length, and the same length as each of the sides of Triangle I from which they are formed.

Further, taking point ϙ, let’s draw a line segment straight down through Triangle I through point κ and all the way down through Square IV (□βαδε) to point λ, dividing the square into two rectangles, Rectangles V (▯καδλ) and VI (▯βκλε). Now, also in lighter grey, we have two larger non-right triangles, Triangles VII (△φαβ) and VIII (△ϙαδ), by drawing line segments from point φ to point β (line segment φβ, or φβ) and from point ϙ to point δ (ϙδ). Finally, also in lighter grey, we draw line segments from point α to point ι (αι) and from point ϙ to point ε (ϙε) to create another pair of smaller non-right triangles, Triangles IX (△αβι) and X (△ϙβε). (Usually, a line is placed above the endpoint letters to signify a line segment, but that type of font is not easily available on Tumblr, so I used crossout print instead.)

Note that the upper left corner of Square IV (angle βαδ, or ∠βαδ) and the lower left corner of Square III (∠φαϙ) both meet at point α and because they are both corners of squares are both right angles. So because Triangles VII and VIII have a common corner at point α, their angles both measure 90º (π/2 radians) plus the angle of the corner of Triangle I at point α (∠ϙαβ) and, therefore, both angles of the corners of Triangles VII (∠φαβ) and VIII (∠ϙαδ) that meet at point α are equal.

Because the side on the left of Triangle VII (φα) and the side on the top side of Triangle VIII (αϙ) both also lie on sides of Square III and both are of length b, and the bottom side of Triangle VII and the left side of Triangle VIII lie on sides of Square IV and both measure length c, and the angles of both triangles that meet at point α are equal, both Triangles VII and VIII are congruent to one another in that all their sides and all their angles are equal, and, therefore, we can assign the letter d to the length of the diagonal sides of both triangles.

Because the line starting at point ϙ going down to point κ and continuing down to point λ (ϙκλ) is a straight line parallel to left side of Square IV (αδ), that is (ϙκλ ‖ αδ), which is the same as the left side of Triangle VIII, measuring length c, and the top side of Rectangle V (αϙ) is parallel to its bottom side (δλ, or αϙ ‖ δλ), both each measuring length f, which is the height of Triangle VIII, therefore its area (½ cf) is half the area of Rectangle V (cf). By the way, if you would like to know the derivation of the triangle area formula, see my previous blog entry.

Further, since the line segment starting at point γ, on the right side of Square III, going to point ϙ and continuing to point β (γϙβ) is a straight line segment parallel to the left side of Square III (φα, or γϙβ ‖ φα), Triangle VII with a base of b and a height of c is half the area of Square III (½ bc = ½ b²), and is therefore, Triangle VIII with a base of c and a height of f is also half the area of Square III (½ cf = ½ b²), which is also half the area of Rectangle V (½ cf = ½ b²). Therefore, the areas of Square III and Rectangle V are equal (b² = cf).

Finally, since the line segment starting at point α, on the left side of Triangle I, going to point ϙ and continuing to point η, on the top side of Square II is a straight line segment parallel to the bottom of Square II (αϙη ‖ βι), Triangle IX has base and height a and, therefore, area ½ a², and the line segment starting at point ϙ, going through point κ and ending at point λ is a straight line segment parallel to the right side of Rectangle VI, Triangle X has base c and height g and, therefore, area ½ cg, and both Triangles IX and X are congruent to each other and, therefore, their areas are equal (½ a² = ½ cg) and, therefore, Triangle X is half of the area of Rectangle VI, and, therefore, both Square II and Rectangle VI have the same area (a² = cg). Therefore, Square IV has the same area as the sum of the areas of Squares II and III (a² + b² = c²). QED

But, as I said, there are thousands of proofs of the Pythagorean Theorem. Next time, we will cover one such proof recently discovered by two high school girls.

Works Cited:

Friberg, Jöran. "Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean Triples, and the Babylonian Triangle Parameter Equations." Historia Mathematica 8 (1981): 277-318.

Høyrup, Jens. "Pythagorean 'Rule' and 'Theorem' – Mirror of the Relation Between Babylonian and Greek Mathematics." Homepage of Jens Høyrup of Roskilde University. Jens Høyrup. 1999. http://akira.ruc.dk/~jensh/Publications/Pythrule.pdf (accessed 2024).

Neugebauer, Otto. The exact sciences in antiquity (2nd ed.). Mineola, NY: Courier Dover Publications., 1969.

Wikipedia "Pythagoras" http://en.wikipedia.org/wiki/Pythagoras , (accessed 2024).

Wikipedia "Pythagorean Theorem" http://en.wikipedia.org/wiki/Pythagorean_theorem , (accessed 2024).

Coming soon: my new blog about Philosophy, Mythology, Religion, and Politics, also in Spanish and English. It's the Aristotelian, and it's available at the-aristotelian.tumblr.com

[factomaniac]

Locura Matemática Nº 3: El Teorema de Pitágoras No Fue Descubierto por Pitágoras y Otros Hechos al Respecto

a² + b² = c²

miércoles, el 12 de junio de 2024, Chicagolandia, IL

(ediciones menores 13 de junio de 2024)

Los historiadores de las matemáticas mesopotámicas han establecido que, a pesar del nombre que es conocido por hoy, el teorema de Pitágoras era ampliamente conocido en el antiguo Imperio Babilónico que existía desde el siglo XX al XVI antes de Cristo, más de 1,000 años antes de Pitágoras de Samos, el homónimo de la teorema, fue incluso nació a mediados del siglo VI aC en la isla griega de Samos o la ciudad de Tyre en Lebanón del día presente (Wikipedia “Teorema de Pitágoras” 2024, Neugebauer 1969, Friberg 1981, Hørup 1998, Robson 2008, Wikipedia “Pitágoras” 2024, Porphyry 2014).

El teorema de Pitágoras afirma que en cualquier triángulo rectángulo, un triángulo que contiene un ángulo recto (un ángulo de 90° –noventa grados– o π/2 radianes), el área de un cuadrado donde cada lado es la longitud de la hipotenusa del triángulo (el lado del triángulo opuesto al ángulo recto) es igual a la suma de las áreas de los dos cuadrados donde cada lado de cada cuadrado es la longitud de cada uno de los otros lados del triángulo, que son perpendiculares entre uno a otro.

Por cierto, la palabra hipotenusa viene dirécto del latín hypotenusa (“jipoteNUsa”), que en última instancia tiene su origen en el griego antiguo ἡ ὑποτείνουσα (“jē jipoTEInusa”), que significa “el [lado] extendido por debajo [del ángulo recto]” porque, en la época griega de antigüedad, los triángulos rectángulos tendían a dibujarse con el ángulo recto apuntando hacia arriba, por lo tanto, la hipotenusa parecía estirada debajo de los otros dos lados que formaban el ángulo recto (Wikipedia “Hipotenusa” 2024, Liddle, Scott, Jones 1940/Perseus Project 2024, Diccionario de Etimología en línea “Hipotenusa” etymonline.com 2024).

Aunque normalmente este teorema se expresa como algo así como “el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los otros dos lados,” y se escribe algebraicamente como a² + b² = c² hoy en día, en la antigüedad, originalmente se construyó geométricamente con cuadrados reales en los lados del triángulo rectángulo. Sorprendentemente, existen miles de demostraciones geométricas y algebraicas del teorema de Pitágoras. Abajo se muestra una prueba geométrica moderna muy sencilla.

Además de servir visualmente como prueba del teorema de Pitágoras, la ilustración anterior también constituye un buen punto de partida para una prueba algebraica del mismo. Con referencia al segundo cuadro de la ilustración con el cuadrado c² en el centro, observe que los lados de todo el cuadro miden cada uno a + b. Por lo tanto, su área se puede encontrar elevando al cuadrado esta expresión: (a + b)². Observe también cómo se puede encontrar el área del marco sumando el área del cuadrado c² a las áreas de cada uno de los cuatro triángulos, ½ab: c² + 4(½ab). El teorema de Pitágoras aparece simplemente escribiendo una ecuación que iguala estas dos expresiones entre uno a otro.

(a + b)² = c² + 4(½ ab) → a² + 2ab + b² = c² + 2ab → a² + b² = c²

Por cierto, la ecuación del teorema de Pitágoras también se puede reordenar para encontrar la longitud de uno de los lados de un triángulo rectángulo sabiendo la longitud de los otros dos lados.

∵ a² + b² = c², c = √(a² + b² ), a = √(c² - b² ), b = √(c² - a² ) (∵ significa “porque” y √(x) significa "la raíz cuadrada de x").

Originalmente, Euclides demostró este teorema tomando un triángulo rectángulo con el ángulo recto apuntando hacia arriba y la hipotenusa como base en la parte inferior y luego, como mencioné anteriormente, haciendo cuadrados con los tres lados del triángulo cuyo cada lado propio es la longitud del respectivo lado del triángulo a partir del cual está formado.

Aunque estoy presentando lo que es esencialmente la demostración del teorema de Pitágoras por parte de Euclides, le daré mi propio giro al referirme a los puntos, líneas y formas de una manera muy diferente a como lo haría se realiza en geometría clásica. Porque una cosa que recuerdo que me resultó confusa cuando aprendí geometría clásica en primaria y secundaria fue la referencia a las formas por los puntos que forman sus esquinas, como referirse a una forma como triángulo ABC—o peor aún, △ABC—porque contiene los puntos A, B y C, o decir que una figura es congruente con otra porque contienen lados proporcionales que se encuentran en puntos que forman los mismos ángulos. Siempre me ha parecido desconcertante la semántica y el vocabulario de la geometría clásica en comparación con, digamos, el álgebra o incluso el cálculo. Por lo tanto, los puntos tendrán letras griegas minúsculas, se hará referencia a las longitudes de las líneas utilizando letras romanas minúsculas y las formas se representarán con números romanos. (Por favor nota bien que usaré la notación tradicional también mi propia notación en orden de evitar confusión.)

Primero, tenemos el triángulo I en gris oscuro (tradicionalmente definido por los puntos ϙ [kopa, pronunciado “CO-pa,” una letra griega arcaica que ahora solo se usa como número], α y β, o simbólicamente como △ϙαβ) con lados de longitudes a, b y c, a es la longitud del lado del triángulo en el lado derecho del ángulo recto, b es la longitud del lado izquierdo del ángulo recto y c es la longitud de la hipotenusa, al estilo de los antiguos griegos, en la parte inferior del triángulo que forma su base. A continuación, están los cuadrados en blanco (cuadrados II [□ϙηιβ], III [□αφγϙ] y IV [□βαδε]—ver la llave de unión en la parte inferior del cuadrado IV) formados a partir de cada uno de los lados del triángulo I, todos cuyos lados, por definición, tienen exactamente la misma longitud de uno a otro y la misma longitud que cada uno de los lados del triángulo I del que están formados.

Además, tomando el punto ϙ, dibujemos un segmento de línea recta que pase por el triángulo I pasando por el punto κ y hasta el cuadrado IV (□βαδε) hasta el punto λ, dividiendo el cuadrado en dos rectángulos, los Rectángulos V (▯καδλ) y VI ( ▯βκλε). Ahora, también en gris más claro, tenemos dos triángulos no rectángulos más grandes, los triángulos VII (△φαβ) y VIII (△ϙαδ), dibujando segmentos de recta desde el punto φ al punto β (segmento de recta φβ, o φβ) y del punto ϙ al punto δ (ϙδ). Finalmente, también en gris más claro, dibujamos segmentos de recta desde el punto α hasta el punto ι (αι) y desde el punto ϙ hasta el punto ε (ϙε) para crear otro par de triángulos no rectángulos más pequeños, los triángulos IX (△αβι) y X (△ϙβε). (Tipicalmente, se escribe un segmento de recta por poniendo las letras de los puntos finales con una línea encima de ellas, pero esta característica no está fácilmente disponible en Tumbr, en lugar de eso por lo que puse las letras de los puntos finales en una fuente tachada.)

Tenga en cuenta que la esquina superior izquierda del cuadrado IV (ángulo βαδ o ∠βαδ) y la esquina inferior izquierda del cuadrado III (∠φαϙ) se encuentran en el punto α y, debido a que ambas son esquinas de cuadrados, ambos son ángulos rectos. Entonces, debido a que los triángulos VII y VIII tienen una esquina común en el punto α, sus ángulos miden ambos 90º (π/2 radianes) más el ángulo de la esquina del triángulo I en el punto α (∠ϙαβ) y, por lo tanto, ambos ángulos de las esquinas de los triángulos VII (∠φαβ) y VIII (∠ϙαδ) que se encuentran en el punto α son iguales.

Debido a que el lado de la izquierda del triángulo VII (φα) y el lado del lado superior del triángulo VIII (αϙ) ambos también se encuentran en lados del cuadrado III y ambos tienen longitud b, y el lado inferior del triángulo VII y el lado izquierdo del triángulo VIII se encuentran en lados del cuadrado IV y ambos miden longitud c, y los ángulos de ambos triángulos que se encuentran en el punto α son iguales, ambos triángulos VII y VIII son congruentes entre sí en que todos sus lados y todos sus ángulos son iguales, y, por tanto, podemos asignar la letra d a la longitud de los lados diagonales de ambos triángulos.

Porque la recta que comienza en el punto ϙ bajando hasta el punto κ y continúa bajando hasta el punto λ (ϙκλ) es una recta paralela al lado izquierdo del cuadrado IV (αδ, es decir ϙκλ ‖ αδ), que es igual al lado izquierdo del Triángulo VIII, que mide la longitud c, y el lado superior del rectángulo V (αϙ) es paralelo a su lado inferior (δλ, o αϙ ‖ δλ), ambos miden cada uno la longitud f, que es la altura del triángulo VIII, por lo tanto su área (½cf) es la mitad del área del rectángulo V (cf). Por cierto, si deseas conocer la derivación de la fórmula del área del triángulo, consulta mi entrada anterior de blog.

Además, dado que el segmento de recta que comienza en el punto γ, en el lado derecho del cuadrado III, va al punto ϙ y continúa hasta el punto β (γϙβ), es un segmento de recta paralelo al lado izquierdo del cuadrado III (φα, o γϙβ ‖ φα), el triángulo VII con base b y altura c es la mitad del área del cuadrado III (½ bc = ½ b²), y es por lo tanto, el triángulo VIII con base c y altura f es también la mitad del área del cuadrado III (½ cf = ½ b²), que también es la mitad del área del rectángulo V (½ cf = ½ b²). Por lo tanto, las áreas del cuadrado III y del rectángulo V son iguales (b² = cf).

Finalmente, dado que el segmento de recta que comienza en el punto α, en el lado izquierdo del triángulo I, va al punto ϙ y continúa hasta el punto η, en la parte superior del cuadrado II hay un segmento de recta paralelo a la parte inferior del cuadrado II (αϙη ‖ βι), el triángulo IX tiene base y altura a y, por tanto, área ½ a², y el segmento de recta que comienza en el punto ϙ, pasa por el punto κ y termina en el punto λ es un segmento de recta paralelo al lado derecho del rectángulo VI, el triángulo X tiene base c y altura g y, por tanto, área ½ cg, y ambos triángulos IX y X son congruentes entre sí y, por tanto, sus áreas son iguales (½ a² = ½ cg) y, por lo tanto, el triángulo X es la mitad del área del rectángulo VI y, por lo tanto, tanto el cuadrado II como el rectángulo VI tienen la misma área (a² = cg). Por lo tanto, el cuadrado IV tiene la misma área que la suma de las áreas de los cuadrados II y III (a² + b² = c²). QED

Pero, como dije, hay miles de demostraciones del teorema de Pitágoras. La próxima vez cubriremos una de esas pruebas descubierta recientemente por dos chicas de escuela secundaria.

Obras citadas:

Friberg, Jöran. "Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean Triples, and the Babylonian Triangle Parameter Equations." Historia Mathematica 8 (1981): 277-318.

Høyrup, Jens. "Pythagorean “Rule” and “Theorem” – Mirror of the Relation Between Babylonian and Greek Mathematics." Homepage of Jens Høyrup of Roskilde University. Jens Høyrup. 1999. http://akira.ruc.dk/~jensh/Publications/Pythrule.pdf (accesado 2024).

Neugebauer, Otto. The exact sciences in antiquity (2nd ed.). Mineola, NY: Courier Dover Publications., 1969.

Wikipedia "Pitágoras" http://es.wikipedia.org/wiki/Pit%C3%A1goras (accesado 2024).

Wikipedia "Teorema de Pitágoras" http://es.wikipedia.org/wiki/Teorema_de_Pit%C3%A1goras (accesado 2024).

Veniendo pronto: mi nuevo blog sobre la filosfía, la mitología, la religión, y la política, también en español y inglés. Se llama el aristotélico, y se despense en the-aristotelian.tumblr.com

[factomaniac]

Locura Matemática N° 2: ¿Por qué A = ½ b⋅a para encontrar el área de cualquier triángulo?

martes, el 28 de mayo de 2024, Chicagoland, IL

Hay muchas fórmulas matemáticas que nos dan durante nuestra educación primaria y secundaria y normalmente nadie explica en detalle cómo se derivaron originalmente y por qué funcionan. La fórmula para encontrar el área de cualquier triángulo parece ser una de ellas.

Refiriéndose al primero de mis dibujos digitales anteriores, dado el triángulo en A, para encontrar su área, se puede orientar el triángulo de modo que su lado largo esté en la parte inferior como en B, de modo que el lado de longitud media esté en la parte inferior como en C, o para que el lado corto quede en la parte inferior como en D, luego se mide la longitud del lado inferior (la base) y luego se obtiene la altura midiendo la distancia desde la base hasta la parte más alta del triángulo, y finalmente, se los multiplica uno por otro y se los multiplica por ½ (o se los divide por 2).

Pero ¿por qué funciona esto? Ésa es una pregunta que Euclides respondió en la Antigua Grecia en su obra Los Elementos.

La razón por la que funciona es porque se deriva por tomar el triángulo original (paso 1) y reflejarlo (paso 2) como que el triángulo original y el nuevo formen un paralelogramo cuyo área también es Área = base × altura, pero sin el ½. Sin embargo, si se "endereza" (o se rectifica) el paralelogramo en un rectángulo dibujando líneas perpendiculares a la que hemos seleccionado como base, se puede notar que cualquier área que se perda en un lado del paralelogramo se gana en el otro lado, y viceversa, por lo que el área del rectángulo resultante es exactamente la misma que la del paralelogramo (paso 3). Aquí es donde se deriva la base y la altura del triángulo porque es la misma que la del rectángulo. Luego, debido a que se duplica el triángulo para obtener esta área, se debe cortar esta área a la mitad para obtener el área del triángulo original (paso 4). Esto se puede hacer de varias maneras, pero prefiero cortar el rectángulo en dos triángulos rectángulos. Y el área de uno de los triángulos rectángulos, o la mitad del área del rectángulo, es la misma que el área del triángulo original. QED

Mis otras ilustraciones muestran que no importa qué lado del triángulo original se refleja o qué lado se toma como base. De cualquier manera que se vaya, se debería terminar con la misma respuesta.

[factomaniac]

Math Madness #2: Why does A = ½ bh for finding the area of any triangle?

Tuesday, 28 May 2024, Chicagoland, IL

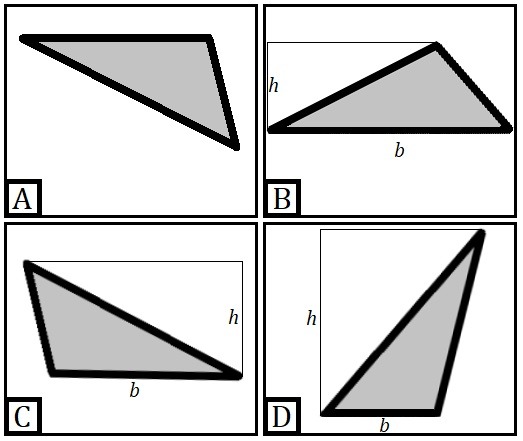
There are a lot of mathematical formulas we are given during our primary and secondary education that nobody usually explains in any detail how they were originally derived and why they work. The formula for finding the area of any triangle seems to be one of them.

Referring to the first of my digital drawings above, given the triangle in A, to find its area, you can orient the triangle so that its long side is on the bottom as in B, so that the middle length side is on the bottom as in C, or so that the short side is on the bottom as in D, then you measure the length of the bottom side (the base) and then get the height by measuring the distance from the base to the highest part of the triangle, and finally, you multiply these together and multiply by ½ (or divide by 2).

But why does this work? That is a question Euclid answered in Ancient Greece in his work The Elements.

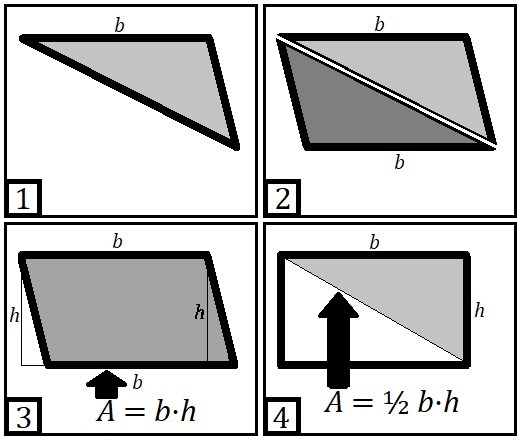
The reason why it works is because it's derived by taking the original triangle (step 1) and mirroring it (step 2) so that the original triangle and the new one form a parallelogram whose area is also Area = base × height, but without the half. However, if we "straighten out" (or rectify) the parallelogram into a rectangle by drawing in lines perpendicular to the one we have selected as the base, you will notice any area we lose on one side of parallelogram is gained on the other side and vice versa, so the area of the resulting rectangle is exactly the same as the parallelogram (step 3). This is where we derive the base and height of the triangle because it is the same as that of the rectangle. Next, because we doubled the triangle to obtain this area, we must halve this area to get the area of the original triangle (step 4). This can be done any number of ways, but I prefer to cut the rectangle into two right triangles. And the area of one of the right triangles, or ½ of the area of the rectangle, is the same as the area of the original triangle. QED

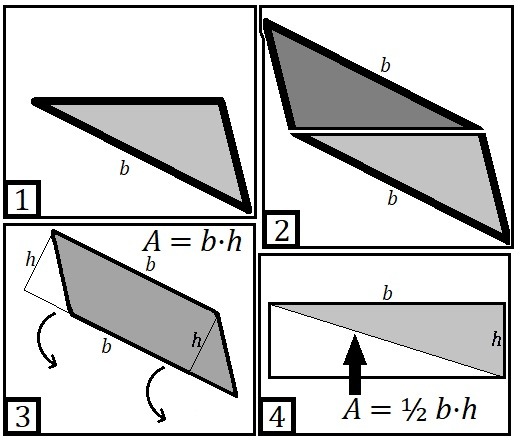
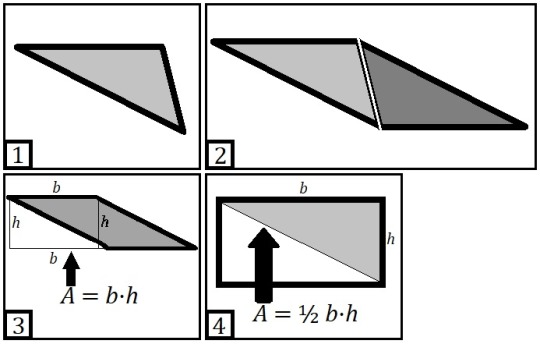
My other illustrations show that it doesn't matter which side of the original triangle is reflected or which side is taken as the base. Any way you go, you should end up with the same answer.

[factomaniac]

Locura Matemática Nº 1: i Es la Raíz Cuadrada de –1, Pero ¿Cuál Es la Raíz Cuadrada de i?

09 julio 2023, Chicagolandia, IL

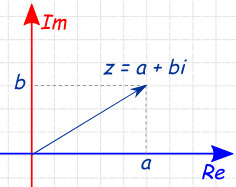
Entonces, si recuerda el álgebra de la escuela secundaria, los números negativos no tienen raíces cuadradas que sean números reales y los números imaginarios (los números reales usados ​​como coeficiente de la unidad imaginaria i, la raíz cuadrada de -1) se desarrollaron, en parte, para dar raíces cuadradas a estos números. (En realidad, se desarrollaron originalmente en el siglo XVI para trabajar con números imaginarios que surgirían en el camino para resolver ecuaciones cúbicas con números reales, pero poder finalmente escribir las raíces cuadradas de números reales negativos resulta ser un beneficio indirecto, pero clave.) Los números complejos son, a su vez, la suma de un número real, a, y un número imaginario, bi, y toman la forma a + bi.

Entonces, como hemos establecido, i es la raíz cuadrada de –1, pero ¿cuál es, a su vez, la raíz cuadrada de i?

En la escuela secundaria, como un adolescente, intenté responder esta pregunta, pero por alguna razón, la respuesta no me llegaba, así que inventé j como la raíz cuadrada de i. Pero entonces, ¿cuál sería la raíz cuadrada de j? Tal vez k? (Mucho más tarde, aprendí sobre los cuaterniones, números cuadridimensionales—de 4 dimensiones—de la forma a + bi + cj + dk, sin embargo, en los cuaterniones, ni j es la raíz cuadrada de i, ni k es la raíz cuadrada de j. Voy a cubrir los cuaterniones en otra publicación de este blog). De todos modos, resultó que estaba completamente en el camino equivocado.

Más tarde, mientras yo estaba en la universidad (mucho antes de descubrir los cuaterniones), resolví este problema usando el Teorema de deMoivre (la potencia de un número complejo en la forma polar, r(cos θ + i sen θ), se puede calcular por elevando r al exponente y multiplicando el mismo exponente por el ángulo: [r(cos θ + i sen θ)]ⁿ = rⁿ(cos nθ + sen nθ) ).

Sin embargo, como descubrí más tarde, encontrar la solución es incluso más fácil que eso. Todo lo que se necesita hacer es establecer el cuadrado de un número complejo genérico, z, en i, calcular el cuadrado de su forma estándar, a + bi, establecer la parte real de este cuadrado en 0 y la parte imaginaria en 1 y luego resuelve las dos ecuaciones resultantes.

(rzcuda(n) = la raíz cuadrada de n)

z² = i -> (a + bi)² = i -> a² + 2abi + b²i² = i -> a² – b² + 2abi = i (i = 0 + 1i) -> (1) a² – b² = 0, (2) 2abi = i -> 2ab = 1

(1) a² – b² = 0 -> (a + b)(a – b) = 0 -> (1A) a + b = 0 -> a = –b, (1B) a – b = 0 -> a = b:: (1) a = ±b

(2) 2ab = 1 -> ab = 1/2 -> aplicando (1B) -> b² = 1/2 -> (2A) b = ±1/rzcuda(2) -> aplicando (1B) al revés: b = a -> (2B) a = ±1/rzcuda(2), aplicando (1A) a (2) -> –bb = 1/2 -> –b² = 1/2 -> (2C) bi = ±1 /rzcuda(2) -> aplicando (1A) al revés: b = –a -> –ai = ±1/rzcuda(2) -> –a = ±1/i rzcuda(2) -> –a = ±– i/rzcuda(2) –> (2D) a = ±i/rzcuda(2)

Por lo tanto, aplicando (2A) y (2B) -> z = a + bi = ±1/rzcuda(2) ± i/rzcuda(2), y de forma redundante, aplicando (2C) y (2D) -> z = a + bi = ±i/rzcuda(2) ± 1/rzcuda(2) = ±1/rzcuda(2) ± i/rzcuda(2).

(Observe cómo las soluciones imaginarias de (2C) y (2D) coinciden con las soluciones reales de (2A) y (2B) al revers. El número de soluciones obtenido, 2, concuerda con el Teorema Fundamental del Álgebra: el número de soluciones de un polinomio es lo mismo que el grado del, o el exponente más alto en el, polinomio. En este caso, estamos tratando con una ecuación de segundo grado, por lo que hay exactamente 2 soluciones. Sin embargo, debido a a² – b² = 0 -> a² = b² y a = ±b, es posible resolver esto creando una ecuación de cuarto grado usando también 2ab = 1: b⁴ = 1/4 -> b = ±rz4a(1/4) = ±1/rzcuda(2), ±i/rzcuda(2). Sin embargo, esto crea un conjunto de soluciones engañoso en el que las soluciones positivas podrían mezclarse y combinarse con las negativas, ya que un polinomio de cuarto grado produciría 4 soluciones. Sin embargo, dado que la ecuación original es de segundo grado , solo hay 2 soluciones verdaderas donde los signos de las partes real e imaginaria coinciden, ya que los desajustes en esos signos darían –i en lugar de i).

Comprobando las 2 soluciones (2 pares de soluciones con cada par idéntico), obtenemos:

(1/rzcuda(2) + i/rzcuda(2))² = 1/2 + 2i/2 + i²/2 = 1/2 + i – 1/2 = i, y

(–1/rzcuda(2) – i/rzcuda(2))² = 1/2 + 2i/2 + i²/2 = 1/2 + i – 1/2 = i

PD Aquellos que estén interesados ​​pueden ver cómo los diferentes signos entre las partes real e imaginaria producirían –i, en lugar de i, aquí hay una verificación de esas soluciones:

(1/rzcuda(2) – i/rzcuda(2))² = 1/2 – 2i/2 + i²/2 = 1/2 – I – 1/2 = –i, y

(–1/rzcuda(2) + i/rzcuda(2))² = 1/2 – 2i/2 + i²/2 = 1/2 – i – 1/2 = –i

[factomaniac]

Math Madness #1: i is the Square Root of –1, but What is the Square Root of i?

01 July 2023, Chicagoland, IL

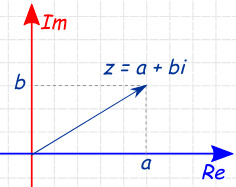
So, if you recall high school algebra, negative numbers do not have any square roots that are real numbers and imaginary numbers (real numbers used as a coefficient of the imaginary unit i, the square root of –1) were developed, in part, to give these numbers square roots. (Actually, they were originally developed in the 1500s to work with imaginary numbers that would crop up along the way to working out real number solutions to cubic equations, but being able to finally write the square roots of negative real numbers happens to be an indirect, but key, benefit.) Complex numbers are, in turn, the sum of a real number a and an imaginary number bi and take the form a + bi.

So, as we've established, i is the square root of –1, but what, in turn, is the square root of i?

Back in high school, my teen self attempted to answer this question, but for some reason, the answer wasn't coming to me, so I invented j as the square root i. But then what would be the square root of j? Maybe k? (Much later, I learned about quaternions, 4-dimensional numbers of the form a + bi + cj + dk, however, in quaternions, neither is j the square root of i, nor is k the square root of j. I'll cover quaternions in another blog post.) Anyway, as it turned out, I was on completely the wrong track.

Later, when I was in college (way before I discovered quaternions), I solved this problem using deMoivre's Theorem (the power of a complex number in polar form, r(cos θ + i sin θ), can be calculated by raising r to the exponent and multiplying the same exponent by the angle: [r(cos θ + i sin θ)]ⁿ = rⁿ(cos nθ + sin nθ) ).

However, as I later discovered, finding the solution is even easier than that. All that needs to be done is to set the square of a generic complex number, z, to i, compute the square of its standard form, a + bi, set the real part of this square to 0, and the imaginary part to 1, and then solve both resulting equations.

(sqrt(n) = the square root of n)

z² = i -> (a + bi)² = i -> a² + 2abi + b²i² = i -> a² – b² + 2abi = i (i = 0 + 1i) -> (1) a² – b² = 0, (2) 2abi = i -> 2ab = 1

(1) a² – b² = 0 -> (a + b)(a – b) = 0 -> (1A) a + b = 0 -> a = –b, (1B) a – b = 0 -> a = b:: (1) a = ±b

(2) 2ab = 1 -> ab = 1/2 -> applying (1B) -> b² = 1/2 -> (2A) b = ±1/sqrt(2) -> applying (1B) in reverse: b = a -> (2B) a = ±1/sqrt(2), applying (1A) to (2) -> –bb = 1/2 -> –b² = 1/2 -> (2C) bi = ±1/sqrt(2) -> applying (1A) in reverse: b = –a -> –ai = ±1/sqrt(2) -> –a = ±1/i sqrt(2) -> –a = ±–i/sqrt(2) –> (2D) a = ±i/sqrt(2)

Therefore, applying (2A) and (2B) -> z = a + bi = ±1/sqrt(2) ± i/sqrt(2), and redundantly, applying (2C) and (2D) -> z = a + bi = ±i/sqrt(2) ± 1/sqrt(2) = ±1/sqrt(2) ± i/sqrt(2).

(Notice how the imaginary solutions of (2C) and (2D) match the real solutions of (2A) and (2B) in reverse. The number of solutions yielded, 2, agrees with the Fundamental Theorem of Algebra: the number of solutions of a polynomial is the same as the degree of, the highest exponent in, the polynomial. In this case, we are dealing with a second degree equation, so there are exactly 2 solutions. However, because of a² – b² = 0 -> a² = b² and a = ±b, it is possible to solve this by creating a fourth degree equation also using 2ab = 1: b⁴ = 1/4 -> b = ±4thrt(1/4) = ±1/sqrt(2), ±i/sqrt(2). However, this creates a misleading solution set where the positive solutions could be mixed and matched with the negative ones, as a fourth degree polynomial would yield 4 solutions. However, since the original equation is second degree, there are only 2 true solutions where the signs of the real and imaginary parts match, as mismatches in those signs would give –i instead of i.)

Checking the 2 solutions (2 pairs of solutions with each pair identical), we get:

(1/sqrt(2) + i/sqrt(2))² = 1/2 + 2i/2 + i²/2 = 1/2 + i – 1/2 = i, and

(–1/sqrt(2) – i/sqrt(2))² = 1/2 + 2i/2 + i²/2 = 1/2 + i – 1/2 = i

PS Those who are interested can see how differing signs between the real and imaginary parts would yield –i, instead of i, here is a check of those solutions:

(1/sqrt(2) – i/sqrt(2))² = 1/2 – 2i/2 + i²/2 = 1/2 – I – 1/2 = –i, and

(–1/sqrt(2) + i/sqrt(2))² = 1/2 – 2i/2 + i²/2 = 1/2 – i – 1/2 = –i

[factomaniac]

Las cuentas de redes sociales de Alex Jones son siendo cerrado

07 agosto 2018, Urbana, IL

reeditado 02 julio 2023

Tengo que admitir que cuando escuché por primera vez que Alex Jones tenía varias cuentas de redes sociales cerradas, al principio pensé que podría haber sido un caso de censura corporativa por consenso. Sin embargo, después de investigar más sobre las acciones de Jones últimamente y sobre las circunstancias particulares de cada uno de los cierres de cuenta de redes sociales, y también la definición legal de incitación, he llegado a creer que Alex Jones debería considerarse a si mismo muy afortunado. Su última serie de acrobacias, en la que apuntó directamente a un número de personas específicas que van desde celebridades de Hollywood a padres y maestros que sobrevivieron al incidente Sandy Hook, aunque sus hijos no lo hicieron, al fiscal especial Robert Mueller e implicaron que estas personas deberían ser hostigadas o incluso agredido, me hace preguntarme si los fiscales de varias jurisdicciones podrían, de hecho, acusar justificadamente a Jones de incitación a cometer extorsión, coacción y/o agresión. Además, las corporaciones de medios sociales involucradas no son agencias gubernamentales, sino entidades privadas que pueden cerrar cuentas por cualquier razón que sientan que es suficiente. Por lo tanto, esta serie de cierres de cuentas no es en modo alguno una censura gubernamental, sino las acciones de un grupo de corporaciones realizadas debido a lo que siento es una reacción más que justificada a la serie de atroces declaraciones de Alex Jones.

[factomaniac]

Alex Jones gets his social media shut down

06 August 2018, Urbana, IL

I have to admit that when I first heard about Alex Jones having various social media accounts shut down, at first I thought it might have been a case of corporate censorship by consensus. However, upon doing more research on Jones's actions of late as well as the particular circumstances of each one of the social media account shutdowns, as well as the legal definition of incitement, I have come to believe that Alex Jones should consider himself quite lucky. His latest series of stunts, in which he directly targeted a number of specific people ranging from Hollywood celebrities to parents and teachers who survived the Sandy Hook incident, though their children did not, to special prosecutor Robert Mueller and implied that these people should be harassed or even assaulted, leaves me wondering if prosecutors of various jurisdictions could, in fact, justifiably charge Jones with incitement to commit extortion, coercion, and/or assault. Additionally, the social media corporations involved are not government agencies, but private entities that can close accounts for any reason they feel is sufficient. Therefore, this series of account shutdowns is not in any way government censorship, but the actions of a group of corporations done due to what I feel is a more than justified reaction to Alex Jones's series of heinous statements. Here are some links for reading material:

http://en.wikipedia.org/wiki/Incitement

http://en.wikipedia.org/wiki/Brandenburg_v._Ohio

http://variety.com/2018/digital/news/youtube-deletes-alex-jones-infowars-videos-1202886565/

http://www.npr.org/2018/08/06/636030043/youtube-apple-and-facebook-ban-infowars-which-decries-mega-purge

http://www.adl.org/resources/backgrounders/alex-jones-five-things-to-know

http://www.newsweek.com/alex-jones-threatens-shoot-pedophile-robert-mueller-accuses-zuckerberg-1038500

[factomaniac]

The 1980s New Wave Band That Accidentally Named Themselves After a Gruesome Effect Caused by a Weapon of War

19 July 2018, Urbana, IL

(minor edit: 02 July 2023)

At our nearby McDonald's, I have yet again been infected with another earworm from a past decade. They continuously play a satellite radio station that puts on nothing but songs from the 1980s and, for whatever reason, have seen fit to play the 1983 song "True" by Spandau Ballet quite a number of times lately. I have since re-acquainted myself with the band and the song, perhaps for the first time since my middle school days of yore, when I first heard it.

The most interesting fact about the band, I believe, is their name, and what I have, after some painstaking Internet research, discovered is ultimately the origin of this band's name. Spandau ("SHPON-dow," first syllable rhymes with "on," in German anyway, and the last one rhymes with "cow,") is a borough in western Berlin, Germany. There was a prison there until 1987 and, while some people have posted on various sites that the origin of the phase "Spandau ballet" is from the apparent dance some Nazi war criminals would do while they were hanged just after World War II, this attribution turned out to be completely false. As anyone who knows about the aftermath of the Second World War could tell you, the trials for the Nazi war criminals were held in Nuremberg and all of the hangings also took place in Nuremberg, not Spandau. In fact, the only connection the Berlin borough has to the Nazi criminals is that a few of them were imprisoned there. That's all.

Nonetheless, if we go back a few decades, we will find a machine gun developed in Spandau a few years prior to the First World War officially known as Maschinengewehr 08 ("Machine Gun 08," enumerated after the year it was first made, 1908), or MG 08, which was nicknamed simply "the Spandau," and was used extensively by the Germans throughout World War I. Many soldiers noticed the powerful force the ammunition shot from the gun had upon the bodies of the victims of war shot using this formidable weapon. With enough practice, many shooters noticed that it was possible to make people spin with flailing arms and appear to pirouette, or to do "the Spandau ballet," as they were in the process of being killed by the bullets riddling their bodies. Although I have not found any actual source that could give me a reference to an original record from the time of WWI or near it using the term in such a way that explained its origin, I have viewed enough derivative sources that I am satisfied that this is the ultimate origin, as macabre as it may be, of this phrase.

P.S. By the way, the band's official story about the source their name is that they got it from a piece of graffiti a friend of theirs saw in the restroom inside a dance club in Berlin. They say they just thought the phase sounded good as a band name and they never intended to make any reference to any type of gallows humor. I believe them and that they had no idea of gruesome origin of the phrase.

[factomaniac]

El Grupo del Estilo Nueva Ola de Rock de la Década de 1980 que Escojó Accidentalmente un Nombre Originado del Efecto Espantoso de un Arma de la Guerra

En nuestro McDonald's cercano, una vez más me infectaron con otro gusano musical desde una última década. Continuamente, se tocan una estación de radio satelital que no pasa más que canciones de la década de 1980 y, por alguna razón desconocida, se decidió tocar la canción de 1983 "True" ("Cierto") de Spandau Ballet varias veces últimamente. Desde está vez, me he vuelto a familiarizar con la banda y la canción, a la mejor, para la primera vez desde mis días lejos en el pasado de la escuela intermedia, cuando recién lo escuché.

El hecho más interesante sobre la banda, creo, es su nombre, y lo que tengo, después de una minuciosa investigación en Internet, descubierta es, en última instancia, el origen del nombre de esta banda. Spandau (pronuncido "SHPAN-dau" en aleman) es una comunidad en el oeste de Berlín, Alemania. Hubo una prisión allí hasta 1987 y, mientras algunas personas han publicado en varios sitios que el origen de la frase "Spandau ballet" es del baile aparente que algunos criminales nazis de guerra harían mientras fueron ahorcados justo después de la Segunda Guerra Mundial, esta atribución resultó ser completamente falso. Como cualquiera que sepa acerca de las secuelas de la Segunda Guerra Mundial podría decirle, los juicios de los criminales de guerra nazis se llevaron a cabo en Nuremberg y todas las ejecuciones también tuvieron lugar en Nuremberg, no en Spandau. De hecho, la única conexión que el distrito de Berlín tiene con los criminales nazis es que algunos de ellos fueron encarcelados allí. Eso es todo.

Sin embargo, si retrocedemos algunas décadas mas, encontraremos una ametralladora desarrollada en Spandau unos años antes de la Primera Guerra Mundial conocida oficialmente como Maschinengewehr 08 ("Ametralladora 08", enumerada después del año en que se hizo por primera vez, 1908), o MG 08, que fue apodado simplemente "la Spandau", y fue utilizado ampliamente por los alemanes durante la Primera Guerra Mundial. Muchos soldados notaron la poderosa fuerza que la munición disparó desde el arma sobre los cuerpos de las víctimas de la guerra usando esta formidable arma. Con suficiente práctica, muchos tiradores notaron que era posible hacer que la gente girara con los brazos temblorosos y pareciera bailar piruetas, o hacer "el ballet Spandau", ya que estaban en el proceso de ser asesinados por las balas que acribillaron sus cuerpos. Aunque no he encontrado ninguna fuente real que pudiera darme una referencia a un registro original desde la Primera Guerra Mundial o cerca de ella utilizando el término de tal manera que explicara su origen, he visto suficientes fuentes derivadas que estoy satisfecho de que este es el origen último, tan macabro como puede ser, de esta frase.

P.D. Por cierto, la historia oficial de la banda sobre la fuente se llama así porque la obtuvieron de un grafiti que un amigo suyo vio en el baño dentro de un club de baile en Berlín. Dicen que simplemente pensaron que la fase sonaba bien como el nombre de una banda y que nunca tuvieron la intención de hacer ninguna referencia a ningún tipo de humor negro. Los creo y también creo que no tenían idea del origen espantoso de la frase.

[factomaniac]

Albert Einstein y Su Cita Profética Que No Era Ni en Realidad Profética Ni Actualmente Suya

Después de investigar un poco en Internet, mi esposa y yo descubrimos que se rumorea que Albert Einstein dijo una vez: "Temo que el día en que la tecnología supere nuestra interacción humana, el mundo tendrá una generación de idiotas. " En ese momento le comenté a mi esposa que, asumiendo que la cita y la atribución eran ciertas, era extremadamente profético de su parte expresarlo, casi hasta el punto de acusarlo de tener habilidades psíquicas. Sin embargo, según Snopes.com, no existe un registro históricamente confiable de Einstein alguna vez diciendo esto. Las únicas fuentes conocidas que le atribuyen estas palabras se publicaron a mediados de la década de 1990 o más tarde. De todos modos, sí expresó varias veces arrepentimiento por lo impersonal que se han vuelto nuestras vidas debido a la tecnología. En una carta a Otto Juliusburger en 1948, dijo: "Creo que el abominable deterioro de los estándares éticos se debe principalmente a la mecanización y despersonalización de nuestras vidas, un subproducto desastroso de la ciencia y la tecnología. ¡Nostra culpa!" Pero esto está tan cerca cuando llegó a expresar una idea como la aparentemente profética al parecer erróneamente atribuida a él.

(Este artículo fue traducido personalmente por el autor con un poco de ayuda de Google Translate)

[factomaniac]

Albert Einstein and the Prophetic Quote Attributed to Him That Was Neither Actually Prophetic Nor Actually His

After some amount of research on the Internet, my wife and I discovered that there has been a rumor going around that Albert Einstein once said, "I fear the day that technology will surpass our human interaction. The world will have a generation of idiots." At the time I remarked to my wife that, assuming the quote and attribution to be true, it was extremely prophetic of him to express it, almost to the point of accusing him of having psychic abilities. As it turns out, however, according to Snopes.com, there is no historically reliable record of Einstein ever saying this. The only known sources that attribute these words to him were all published in the mid-1990s or later. Nonetheless, he did express a number of times regret for how impersonal our lives have become because of technology. In a letter to Otto Juliusburger in 1948, he said, "I believe that the abominable deterioration of ethical standards stems primarily from the mechanization and depersonalization of our lives, a disastrous byproduct of science and technology. Nostra culpa!” But this is as close as he got to expressing such an idea as the seemingly-prescient one apparently-erroneously attributed to him.