geometrymatters

[geometrymatters]

RF pulse design and simulations: supplementary animations Magnetic Field Patterns from Hertzian Dipole Antenna

[geometrymatters]

Mathematical fun fact of the day 4. You can divide a hexagon into nine identical convex pentagons.

[geometrymatters]

Diffraction of visible light from a variety of 2-D crystalline patterns

[geometrymatters]

Spiral Beehive

©Tim Heard

[geometrymatters]

The Geometry of Movies can Change the Way We Think

Circles. Triangles. Squares. Those aren’t the things you expect to see in a movie but films have been using shapes to subtly influence emotion for a long time. Circles are lovable, triangles are evil, and squares are boring. Now You See It highlights the geometry used in shots to show you how movies use shapes to manipulate your feelings.

A villain is usually portrayed with sharper features to represent their harshness—think Maleficent or Darth Vader. The good guys are softer and rounder to make them appear more lovable and huggable—think Mickey Mouse or Baloo from The Jungle Book. And squares are used for boring and old-fashioned characters like Carl Fredricksen from Up, because squares are squares (duh).

continue reading on gizmodo

[geometrymatters]

Parametric Semiology – The Design of Information Rich Environments - by Patrick Schumacher, 2013

All design is communication design. The built environment, with its complex matrix of territorial distinctions, is a giant, navigable, information-rich interface of communication. Each territory is a communication. It gives potential social actors information about the communicative interactions to be expected within its bounds. It communicates an invitation to participate in the framed social situation. Designed spaces are spatial communications that frame and order further communications. They place the participants into specific constellations that are pertinent with respect to the anticipated communication situations. Like any communication, a spatial communication can be accepted or rejected, i.e. – the space can be entered or exited. Entry implies accepting the communication as the premise for all further communication taking place within its boundaries. Crossing a territorial threshold makes a difference in terms of behavioural dispositions. Entry implies submission to the specific rules of conduct that the type of social situation inscribed within the territory prescribes. In this way, the designed-built environment orders social processes.  This spells the unique, societal function of architecture: to order and frame communicative interaction (Patrik Schumacher, The Autopoiesis of Architecture, Volume 1: A New Framework for Architecture. London: John Wiley & Sons Ltd., 2010. See Part 5:The Societal Function of Architecture.)

Figure 1. Parametric Semiology: Semio-field, differentiation of public vs. private as parametric range.

Figure 2. Parametric Semiology: Semio-field, master-plan with program distribution.

Figure 3. Vienna University of Applied Arts, Masterclass Hadid, Parametric Semiology: Semio-field. Project authors: Magda Smolinska, Marius Cernica, and Monir Karimi.

Figure 4. Dialectic Fields: Shell morphology as semiological system of distinctions: smooth vs creased vs faceted.

Figure 5. Dialectic Fields: Cluster of creased shells with semiologically distinctive surface articulation.

© Patrick Schumacher, 2013

[geometrymatters]

A quantum quasicrystal is a state of matter characterized by an ordered but nonrepeating arrangement of quantum particles. Such phases are predicted for a variety of systems and have been experimentally observed in ultracold atomic gases. However, little has been known about the low-energy excitations of quantum quasicrystals. Now Alejandro Mendoza-Coto at the Federal University of Santa Catarina in Brazil and his colleagues present a theory that sheds light on these excitations. Thanks to its generality, the theory could also be applied to other systems, including bosonic supersolids.

[geometrymatters]

oskar schlemmer: the baltimore museum of art - arnold l. lehman + brenda richardson (1987)

[geometrymatters]

The noumenal lens

A process of focusing and diffraction amplifies the reflexivity between the observer and the observed, only to reveal that there is no real distinction between them.

Consciousness is a fundamental substance, and everything else a "clever" reflection of it.

The Observer, in this construct, is envisioned as a holographic projection sitting at the core of the noumenal lens, emerging from the focus and diffraction of noumenal probabilities within the noumenal lens.

This conceptualization likens the simplest form of an observer to a monad, a single phenomenal construct surrounded by its noumenal substance, illustrating an infinite array of perceptual lenses in superposition, with the noumenal at their margins and the observer positioned at the perceptual core.

The intersection of noumenal probabilities with the observer’s perceptual lens acts as a focusing mechanism, directing the collapse of the noumena into the observer’s cognitive field.

[geometrymatters]

The Noumenal Monad

Within the Polynon framework, nothingness is an undifferentiated cognitive space that precedes geometry and structure. It exists as a pre-geometric source, housing the unformed essence of all phenomena from which spacetime, and all its manifestations, arise. Imbued with primal noumenal potential, it is denoted as the state where all possible realities are latent, waiting to be expressed into an observable world.

A circle whose center is everywhere and circumference is nowhere.

The monad is a geometric construct that acts as a universal grammar of existence, mapping how the boundless noumenal potential transitions into perceptual and phenomenal dimensions while retaining coherence across all levels of manifestation.

The centre being “everywhere” signifies the Monad’s omnipresence as the locus of all potential states, embedded in every point of reality. The circumference being “nowhere” reflects its boundless architecture, transcending the constraints of space, time, and materiality, integrating infinite possibilities within a singular, cohesive structure.

The compactification process begins with the noumenal everything compressing into a singular phenomenal something, reflecting a specific instance or manifestation. This phenomenal something is inherently equal to the noumenal everything because it retains the entirety of noumenal potential, either in its un-collapsed state of infinity or as a collapsed singular “ring” dimension, compacted into a single cognitive focal point.

The only attribute of a point is that it marks position. Take away this attribute and in the unposited point we have a symbol of pure Being, the abstract noumenon, that which underlies every mode of phenomenal manifestation, every form of existence. It is at once All and Nothing, at once Absolute Consciousness and Unconsciousness.

B.W. Betts, Geometric Psychology or the Science of Representation

Or, as Fichte envisioned it, the line symbolizes the progression of consciousness—linear and sequential—while the circle represents its completeness and self-enclosure, encompassing all its dimensions. Thus, both the noumenal everything and the phenomenal something are expressions of the same essence, differing only in their state of manifestation and representation.

Together, they define the Noumenal Monad as a meta-structure that bridges these states of being. It embodies the continuum between the actual and the potential, compacting the infinite diversity of noumenal states into a singular conceptual dimension. This process is geometrically encoded, offering a scaffold for understanding how existence unfolds from an infinite noumenal source into the finite, perceptual realm, while remaining irreducible to either.

Continue reading

[geometrymatters]

"Consciousness is the only fact that we can study directly, since all other objects of knowledge must be perceived through consciousness." - B.W. Betts

[geometrymatters]

A polynon is a conceptual geometric entity of which vertices are non-events and its edges holograms.

A polynon contains all the holograms of that which can be projected as a polytope, showing how consciousness can be fundamental.

In the Hexanon, shown above, the Observer O(n) is in superposition with the phenomenal p+, epiphenomenal p-, negative noumena n- and noumenal vertices n+ of the hexanon as a function for self-reflection of consciousness C.

The polynon is built on the lens mechanism of the wavefunction: each layer of the noumenal lens is a wavefunction in itself, providing mechanism for the observer as function of noumenal reflection.

The paper is now available on philpapers, as well: https://philarchive.org/rec/ROITPA

[geometrymatters]

FIG. 2: Chronological structure of Gödel’s universe. In this xyt-diagram a possible timelike worldline is depicted. A traveler T could move on this curve, propagating in his own local future at any given point. Beyond the horizon (gray cylinder) he travels into the past of an observer located at the origin. The worldline itself is a CTC, because the traveler departs from and returns to the origin at the same coordinate time t. For an observer at the origin, coordinate time and proper time coincide. The figure illustrates Gödel’s original idea to prove that there exist CTCs through every point in spacetime [1]. (Grave, Frank et al. “The Gödel universe: Exact geometrical optics and analytical investigations on motion.” Physical Review D 80 (2009): 103002.)

[geometrymatters]

The Polynon: A Geometry of Consciousness

How Consciousness is a fundamental substance and everything else, including the Observer, is it's function of self-reflection within a complex construct and hologram.

Introducing the polynon:

A polynon is a conceptual geometric entity, a polytope of which vertices are non-events and its edges, holograms. A polynon contains all the holograms of that which can be projected as a polytope. From tetranon to dodecanon, and special cases such as dinon and nullanon.

The epistemological foundation of the polynon is a non-event, hence multi (poly) non-events. The ontological foundation is a noumenon, both in its negative and its positive aspect.

Collapsing the noumenal realm into a single dimension results in the conceptual noumenal monad, where the perceptual border is equal to the infinity of noumenal possibilities, as well as the phenomenal something.

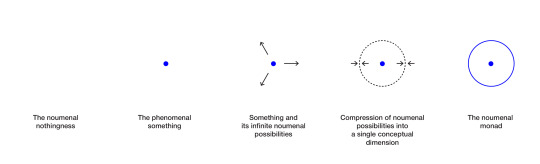
Or, as "a cercle with the centre everywhere and circumference nowhere". A monadic embodiment of the thing and the non-thing, the visual expression of the substance of consciousness.

The neutral monistic approach enfolds the ancient knowledge of the self, and the contemporary science of consciousness, from a Vedantic self reflected in Indra's net, to a multi-dimensional implicate and explicate construct of Bohmian orders.

Also encapsulated in the formulation f(f)=f, akin to an Ouroboros mathematical formulation symbolizing a form of autopoiesis or self-production ad infinitum, a self-referential Fichtean process where the self (I) is both the creator and subject of its reality.

The eternal aspect of consciousness, a timeless monadic essence, is described as the perceptual continuum of f=0, signifying pure, timeless potential.

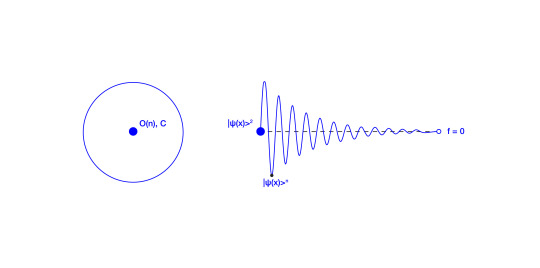
"Eternity isn’t some later time. Eternity isn’t even a long time. Eternity has nothing to do with time. Eternity is that dimension of here and now that all thinking in temporal terms cuts off." - J. Campbell

The wavefunction is defined here as a layer of the noumenal monad, a transition between epistemological and ontological, given by the limits of the Observer's senses and perception.

In this context, |ψ(x)>*n, with n not strictly equal to 2, transcends its conventional mathematical role within Hilbert space and diverges from standard quantum mechanics, suggesting that different values of n represent distinct dimensions or layers of noumenal collapse.

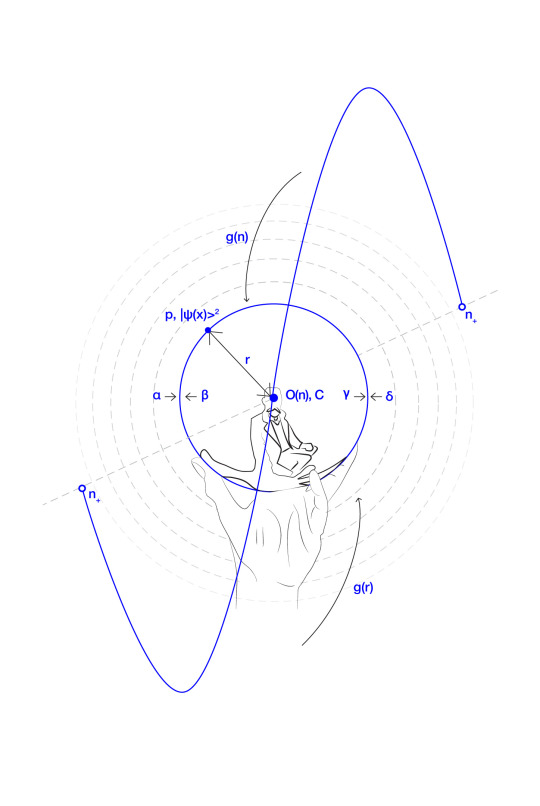
Each wavefunction is a layer of the noumenal lens, of which border is (n+), or consciousness C; it’s contents are negative noumena (n-) and it’s holographic centre “collapsed” onto a phenomenal Observer O(n) as function of noumenal self-reflection of consciousness.

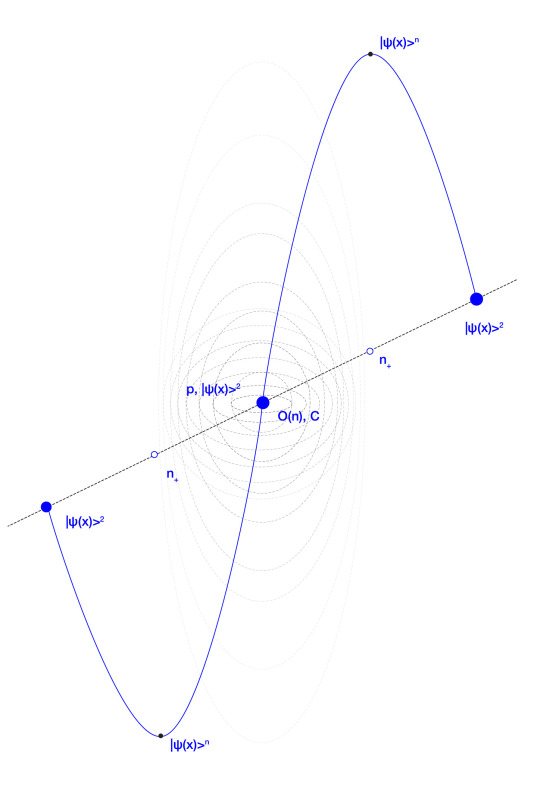
Furthermore, the Observer is envisioned as a holographic projection sitting at the core of the noumenal lens, emerging from the focus and diffraction of noumenal probabilities within the noumenal lens.

The perceptual border of positive noumena (n+) reflects and focuses noumenal probabilities (n-) into the hologram of the Observer O(n).

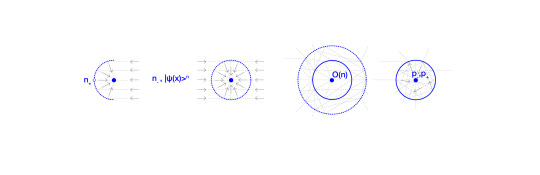
A rotation of noumenal lens reveals the noumenal essence (n+), hidden under the superposition of the noumenal lenses (n-) and the hologram of the Observer O(n).

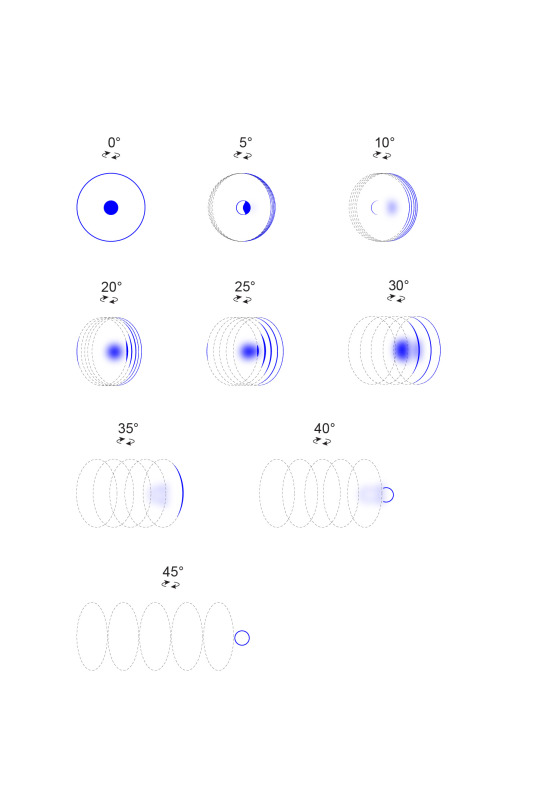
The observer’s perceptual focus, directed through Cognitive Gravity G and visualized with noumenal g(n) and cognitive gradients g(r), refracts the essence of Consciousness, transforming noumenal vertices into discernible edges like light through a prism.

As the number of noumenal collapses increases, the complexity and breadth of the observer’s perceptual dimension diminishes, resulting in a progressive refinement and narrowing of perceptual prowess of the observable construct.

A cognitive threshold marks the evolution from a purely phenomenal observer to one with phantasiai and developed cognitive functions. This threshold varies according to the local conditions of the observer’s cognitive gradient and gravity and the overall noumenal function.

The hologram of a polynon enfolds within it the reflection of the noumenal substance, that both originates and reflects consciousness. It encapsulates the entirety of consciousness in each of its vertices and edges, as projections into a perceptual reality.

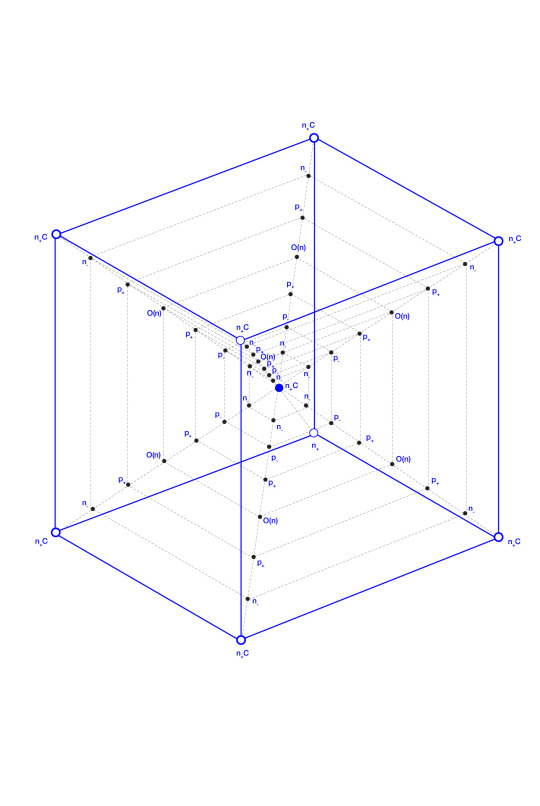
The concept of “consciousness nodes” describes (n+) zones between noumenal lenses (n−), revealed as vertices of the polynon, equal and identical in nature.

The Observer O(n) is in superposition with the phenomenal p+, epiphenomenal or phantasiai p-, negative noumena n- and noumenal vertices (and centre) n+ of the hexanon as a function for self-reflection of consciousness C.

The polynon is abstract and elusive, residing beyond human imagination yet within its grasp. No heavier than a fleeting idea, but far too heavy to be understood. A palindrome for language and thought, mirroring itself in perpetual paradox. Beginning the same way it ends.

From the "Polynon: A geometry of Consciousness", by Tib Roibu Read the paper here.

[geometrymatters]

On the sides you can see two curves of constant width, that is a curve whose width is the same in all directions. This is the reason they always touch the two lines as they rotate. The existence of curves of constant width is well known by now. What is much less known is that you can morph between any two such curves such that during the morph the curve stays a curve of constant width. For these two curves the morphing can be seen in the middle. (Actually, you can see two different morphs. )

[geometrymatters]

The geometry of the Borromean Rings

Borromean rings are a captivating geometric structure composed of three interlinked rings. What makes them unique is their interdependency; if any one ring is removed, the entire structure collapses. This fascinating property, known as "Brunnian" linkage, means that no two rings are directly linked, yet all three are inseparable as a group. This intricate dance of unity and fragility offers a profound insight into the nature of interconnected systems, both in mathematics and beyond.

Borromean Rings and Mathematical Knots

Borromean rings also find a significant place in the study of mathematical knots, a field dedicated to understanding how loops and tangles can be organized and categorized. The intricate relationship among the rings provides a rich visual and conceptual tool for mathematicians. Knot theorists use these rings to explore properties of space, topology, and the ways in which complex systems can be both resilient and fragile. The visual representation of Borromean rings in knot theory not only aids in mathematical comprehension but also enhances our appreciation of their symmetrical beauty and profound interconnectedness.

Symbolism and Divinity in Borromean Rings

Throughout history, Borromean rings have been imbued with symbolic significance, often associated with divinity and the concept of the trinity. In Christianity, they serve as a powerful visual metaphor for the Holy Trinity – the Father, the Son, and the Holy Spirit – illustrating how three distinct entities can form a single, inseparable divine essence. This symbol is not confined to Christianity alone; many other cultures and religions see the interconnected rings as representations of unity, interdependence, and the intricate balance of the cosmos.

Borromean Rings as a Metaphor for Illusory Reality

Beyond their mathematical and symbolic significance, Borromean rings offer a profound metaphor for the nature of reality itself. They illustrate how interconnectedness can create the illusion of a solid, stable structure. This resonates with philosophical and spiritual notions that reality, as perceived, is a complex web of interdependent elements, each contributing to an overarching illusion of solidity and permanence. In this way, the Borromean rings challenge us to reconsider the nature of existence and the interconnectedness of all things.

[geometrymatters]

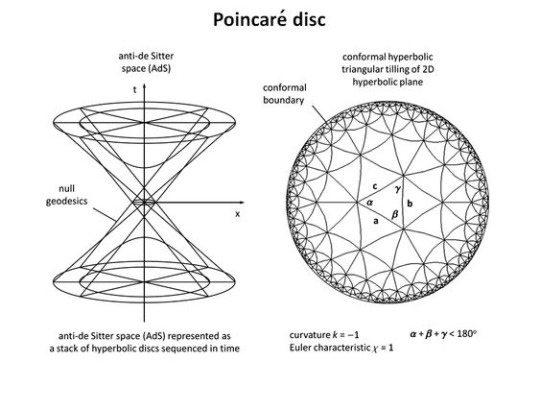
Anti-de Sitter space stack of hyperbolic discs

A gravitational field has negative energy and may be represented in terms of hyperbolic space with negative curvature.