klr

[klr]

Moving to Medium

Hello, blog readers! We’re going to give Medium a try for future blog posts. We’d be grateful if you followed us there.

Psst: there’s a new post waiting for you!

[klr]

Curated work can help develop student understanding

We've been having many conversations with history teachers to understand their challenges and how we can help. Andy wrote about a method we used to structure those conversations: We wrote up short pitches on cards and asked teachers to sort them based on how valuable they seemed.

Each pitch described how students might write and interact with each others' responses to open-ended questions. 

But none of the pitches promised curated responses — responses crafted by Khan Academy to further develop student understanding.

Teachers quickly pointed out that gap. They had many different ways of talking about curated responses: sample work, model work, worked examples, exemplars. But pretty much every teacher agreed that they were indispensable for helping students develop their understanding.

We went back and thought about why curated responses are useful. We came up with 2 reasons:

1. Instruction. Curated responses can do some of the "modeling" that a teacher otherwise might do. For example, a curated response might be designed to make really great use of evidence. It might be annotated in a way that helps students understand what makes this usage exemplary.

2. Scaffolding. Curated responses can be written in a way that makes them perfect for a particular task. For example, a curated response might have a particular weakness to be improved, or it might have a piece missing. In this way, curated responses can make it possible for a student to complete tasks they might not otherwise be able to. In other words, they can increase the zone of proximal development.

Whether they’re designed for instruction, scaffolding, or both, curated responses must be carefully designed to ensure they develop understanding. Fortunately, Khan Academy has a team of talented content specialists up for the challenge.

But what happens when you don’t have content specialists? Is it possible to find curated responses from a pool of un-curated, student-created work?

We think the answer is yes. In aggregate, student engagement (upvotes, highlights) can bubble up exemplary responses. 

And through student markup (tag the thesis, score this based on a rubric), responses can be given context that makes it possible to conduct scaffolded tasks (find the thesis, explain the grade).

But! This only works if students are learning and engaged as they add context to their own responses and the responses of their peers. When does “Highlight the thesis” feel like a game? When does it feel a chore? When does it provoke? When does it bore? 

A lens we continually apply as we explore ideas for marking up peer work is: Does this feel like going to the DMV? If it does, we can safely throw the idea out.

[klr]

Sorting product “baseball cards”: bridging behavioral interviews and prototypes

We’re excited to share a user research method that helped us bridge the gap between wide-ranging behavioral interviews and detailed validation of specific value propositions. We made quick progress by asking teachers to talk through how they’d rank “baseball cards” describing hypothetical products we’d synthesized out of insights from a first round of interviews.

For many months, we’ve been exploring: how might we help students build deep understanding through writing activities on online learning platforms? We’re initially focusing on AP-level history, though we’re trying to build something general. Answering that big question has meant finding good intersecting answers to four separate questions:

Pedagogy. How might we define scaffolds and feedback mechanisms around open-ended activities to best support students in building understanding?

Interface design. How might we design interactions in these online writing activities to support, generate, and execute our pedagogy’s scaffolding and feedback?

Value proposition. How might these kinds of writing activities solve burning problems for teachers and naturally integrate into their practices?

Content creation. How might these writing activities best fit into our broader curricula, and how might we frame their structure so they can be practicably authored at scale?

In this post, we’ll focus on the value proposition question. We were confident that if we succeeded with the pedagogy and interface design questions, we’d be creating something that could really help students. But we felt we could have the most impact reaching students through the rich environment of a classroom—a context which layers on its own significant opportunities and challenges.

We knew that we’d need to deeply understand how these activities might be used in real classrooms, as part of a teacher’s broader mental models, classroom practices, and feedback mechanisms. With that understanding, we could shape the activity’s surfaces so that what happens outside the activity resonates with what happens inside the activity, amplifying both sides. And critically, that understanding would help us frame these activities in a way teachers would be thrilled to use.

We knew that we’d have to talk with plenty of teachers to build the understanding we’d need, so we began by recruiting a few dozen teachers who were willing to chat with us. Our first interviews stayed broad: we asked teachers about their background, environment, practices, values, fears, challenges, dreams. We gleaned all kinds of interesting insights, like:

Most AP classes are now open enrollment (i.e. any student can join) meaning teachers are contending with a huge range of student capacities.

Even in history, many teachers had over a hundred students. Grading a single essay might take weeks.

Teachers were apprehensive of the AP’s increasing emphasis on disciplinary skills over content knowledge; they lacked strong resources for preparing students to e.g. analyze historical continuities across time periods.

They often worked on those skills through peer work in class, but those activities are hard to orchestrate.

There’s so much to cover that homework time has to be spent almost entirely on readings.

After synthesizing these themes and identifying our key personas, we wrote six different pitches for a hypothetical product: different angles, different pain points, different timings. Collectively, they spanned the space of opportunity we saw. Once we had our pitches written out, we formatted them like little product “baseball cards” for easy comparison and arranging.

Then, in another round of interviews with different teachers, we abbreviated the broader user research questions to focus on a card sorting activity. It went like this:

We showed teachers all the cards and explained that they represented hypothetical products.

We asked them to read through them one by one, verbally reacting along the way.

We told them they could try a prototype of one of these products in their class next week and asked which one, if any, they’d be most interested in trying.

We asked them which one seemed least useful. Then we had them rank-order the others in the middle.

Finally, we asked them how often they’d be excited to use each of the cards in their classes.

Their rank-ordering was incredibly useful: it helped us eliminate a few possibilities and shined light on a promising subset of the space. But teachers’ verbal reactions as they read the cards were equally helpful. The pitches prompted teachers to connect those ideas to others in their experience. They connected our cards to existing practices, told related stories from their classroom life, and imagined aloud how to integrate the product. Their words brought the hypotheses alive and helped us share our findings convincingly with stakeholders.

We took all that insight and refined our existing designs to accord with the pitches teachers had been most eager to try. We didn’t just pick the most popular baseball card: the pitches existed as a fulcrum to understand teachers’ mental models and needs. We used what we learned to synthesize a solution that could fulfill several of those cards, as well as others we hadn’t yet written.

For our next phase of interviews, we abbreviated the card sorting activity and focused on introducing teachers to a real prototype. This new set of teachers loved what we’d made (which helped validate our synthesis), and as with the pitches, the prototype prompted the teachers to share more interesting thoughts, feeding our iteration. Meanwhile, we kept our promise with the teachers who’d done the card sorting activity: we set them up with our prototype for a live classroom pilot. More great learning ensued.

It’s always a struggle to build a bridge from behavioral interviews’ broad insights to a viable prototype. By writing these intentionally-distinct “baseball cards,” we turned the initial interviews into something concrete—but not so concrete as a prototype, which often over-constrains the conversation. And while it might have seemed like we could have written those pitches without the initial broad interviews, that too would have constrained the conversation too early. At least to me, this gradual narrowing felt just right.

[klr]

Explain to who?!

Standardized exams frequently ask students to provide explanations.

And this is a good thing! Explanations are great for demonstrating complex understanding.

But in their natural environment, explanations are multiplayer exchanges:

A: “I don’t get it.”

B: “Here, let me explain it to you!”

[...]

B: “Got it?”

A: “Yeah!”

In contrast, exam explanations are single-player, and evaluated by a grader who:

Already knows the material

Has a lot of explanations to get through

As Scott Farrar put it, they ring false:

Exam: Explain how farming practices evolved in the fifteenth century.

Student: Explain to who?! You already know!

These explanations are almost never evaluated in authentic contexts. As a result, we should be suspicious of the evaluations themselves. 

How might we fix this?

Q&A

Authentic explanation happens when the explainee:

doesn’t understand

wants to understand

evaluates whether the explanation helps them understand

In this way, the best way to generate and evaluate authentic explanations is through a Q&A platform.

Many such platforms are available today, but few (none?) are used as the primary way for evaluating student learning.

For that to happen, some structure would have to be necessary; maybe students would be required to explain and be explained to X times per week.

A gamified version of this would look less like StackOverflow or Reddit (leaderboards & reputation systems), and more like Wikipedia or Yelp (celebrating top contributors and people who improve the platform in a variety of ways).

Role-play

Without a vibrant marketplace of authentic questioning and explaining, maybe the next best thing is faking it.

The ELI5 (explain it like I’m 5) subreddit is a good example. It’s a gentle reminder to avoid jargon, and a challenge to find the simplest explanation possible.

In “trade and grade” activities, teachers will print out essay rubrics and ask classmates to grade their peers as if they were exam graders. 

And they’ll spice things up with character motivation:  “Imagine you’re going to have to get through hundreds of these!”

I wonder how role-play might be extended beyond the grader. How might students practice explaining to: 

Someone from 100 years ago?

Someone from Mars?

Your hero? 

Your fiercest opponent?

Expose the process

If a grader is going to evaluate a multi-paragraph essay based on a rubric, might it make more sense for the student to organize their response directly in the rubric? 

Test-takers would be sure they were properly answering the question, and graders would save a bit of time. Wouldn’t this make for a more authentic exchange?  

Or would this compromise some of the explanatory magic? 

And if it would, how does that magic get graded in the first place?

[klr]

Two new long-form reports

If you haven’t seen them already, we’ve recently published two long-form reports synthesizing some of the projects we discuss on this blog. In the tradition of messy thought / neat thought: the blog’s for messy thought; these reports are our neat thought!

Numbers at play: dynamic toys make the invisible visible. What if you had some new way to represent numbers in your head—and manipulate them in your hands—that made certain thoughts easier to think? This report is roughly a theory of the possibilities in digital math manipulatives, demonstrated through a new one we designed.

Playful worlds of creative path: a design exploration. Plenty of grown-up artists, scientists, and engineers find math empowering and beautiful. We wondered:how might we help more kids experience what math lovers experience? We explored designs for a world where everything wears its math on its sleeve—where children can create and have adventures by playing with the numbers behind every object. This report shows those designs and a dozen prototypes.

[klr]

Explanations from alleged masters of shape dissection

We’d just invited a few thousand students to try our latest experiment in online open-ended response activities—a controlled trial with pre- and post-test questions focused on concept transfer. We started reviewing their work, but the data from the control group stopped us in our tracks. We got page after page of responses like this:

This kind of answer wouldn’t be so surprising, except that all of these students had just solved four numerical “find the area of this polygon” problems perfectly, including one with exactly this shape.

We were testing an activity in which students would interact with each others’ open-ended explanations and ideas. They’d learn about finding the area of polygons by dissecting them into simpler shapes.

Our control group watched a video lecture on the subject, then worked through typical textbook-style exercises on the subject, like these:

Plenty of students solved every one of these exercises correctly. Typical standardized tests might suggest that these students had mastered shape dissection. But a third of those students couldn’t give even a partial answer to the “explain why” question above; another third gave poor or incomplete answers.

We didn’t design our experiment to look at this issue: we included these area-finding problems as a “dummy” activity to parallel the richer discussions in our experimental group. Maybe the issue is that the “explain why” prompt involves more algebraic knowledge. Besides, our experimental population is not necessarily representative.

But the intense gap between the procedural and conceptual assessments here still shook me.

Have you ever gotten an “A” in a class but felt you didn’t really understand the material? That seems to be exactly the disparity we’re seeing here. How many numeric-input or multiple-choice tests would exhibit the same problems?

We’ve long discussed our suspicions around scores taken from this kind of problem; we didn’t expect to confront such jarring examples so directly!

[klr]

We asked Khan Academy learners to talk to each other about math

Open response on the internet means breaking away from machine gradable multiple choice or numerical entry as the sole method and representation of student thinking. But if student work is not machine gradable, how can the students receive feedback?

Many modern classroom practices involve facilitated peer interactions: students talking to students in a structured way. What happens when we facilitate peer interactions between learners on Khan Academy?

Our open response project at its heart is:

1. Students respond to a prompt. 2. Students give and receive peer feedback on that work. 3. Students use the peer feedback to revise or extend their original work.

In this trial, we showed students two different methods for solving the area of a trapezoid. (These methods are intentionally set up to provoke comparisons in algebra and geometry. I have done lessons around this since the idea came to me via Dr. Judy Kysh years ago.)

Alma (Sample work)

Beth (Sample Work)

Responding to the Prompt

We asked the trial participants for similarities and differences, and for questions that either they had, or that they could imagine another learner having.

Here are some of the questions they wrote:

I still wonder why they didn't use the formula for the area of a trapezoid: (1/2)(base1+base2)(height).

Can all trapezoids be rotated to form one long parallelogram? Or is it just specific to certain types?

Is one easier to visualize than the other?

A student might ask if we always have to cut the shape in order to find the area.

for alma how you know that yellow triangle is half of (2x3)?

These questions display a variety of mathematical engagements with the prompts. If these were asked in a classroom, they’d be great fodder for a teacher to facilitate class discussions around.

The broad prompts of comparing similarities and differences provide many entry points to students at varying levels. In the questions above, we see a learner approaching from the formula, a student thinking about generalizability of one of the methods, a student wondering about communication (visualization) styles, along with students asking about the underlying pieces of the methods like dissection and area of triangle.

I like this question/comment: I'm not sure that Beth's method makes the problem any simpler, as a parallelogram is just a special trapezoid so she could straightaway use the half-height-times-sum-of-lengths rule.

What fun that could be to bridge this area discussion to the classification of quadrilaterals. The advantage of open response is the ability for many related ideas to be discussed at once.

Peer Feedback

So we took these observations and questions and distributed each to another member of the participant group. For example, this question was seen and answered by a peer:

Question: for alma how you know that yellow triangle is half of (2x3)?

Peer Answer: Alma can know that the yellow triangle is half of 3*2 if she is familiar with the triangle area formula which states that every triangle as an area equal to its height times its base divided by two. This comes out of dividing a parallelogram in 2. To calculate the area of a parallegram you mutiple it width by its heigh. A triangle is just half of parallelogram.

This answer asserts the triangle area formula but goes a little farther: supplying a connection to parallelogram area. Another question and answer pairing shows how a good pairing of peers can help someone appreciate a new point of view.

Question: I wonder why both students did not calculate the area of the trapezoid in one step:Area = 3 x (2+6)/2 Beth's calculation amounts to the same but the rotation etc was not necessary.

Peer Answer: Beth's approach is more suited for those who prefer to visually see their calculations. Whereas Alma's technique breaks the trapezoid into simpler shape which most people would likely know the area formula of. This is useful in situations where one does not know the formula of the area of a certain shape but can discern that it is made up of smaller shapes. Often, these smaller shapes have simpler area formulas. 

But a challenge in all peer interactions, online or not, is ensuring a positive productive relationship. Not all questions and answers were helpful:

Question: whether shapes fit when rotated

Peer Answer: Of course they fit when rotated. I did somwhat the same thing and it worked 

Allowing a user to request new feedback will be important.

An expert teacher with sufficient time may be able to pair students based on which ideas should encounter one another. Currently our prototype has no expert involved. Research from Elena Glassman has demonstrated some of the potential avenues to involve experts and learners at scale. 

While the lack of an expert teacher meant the facilitation was essentially random, it still provided most (in our skewed recruited population) of the participants with a chance to discuss a personally expressed idea.

Synthesizing and Extending

To cap off this activity, we asked participants to synthesize the ideas they’ve written with the work and feedback from others to write about a third method:

Coco (Sample Work)

This work sample is similar to one presented in the current Khan Academy Video on area of trapezoids: (4:00 mark) YouTube, KhanAcademy.org

How might a learner’s mathematical conceptions change when doing open ended response and peer feedback work? How might this supplement or support the “just in time” learner whose google search lands them in Khan Academy’s trapezoid content? How might this supplement or support the “sustained learner” who has progressed through Khan Academy’s geometry course? How about a classroom full of students assigned to participate?

Student response: These ideas helped me see how other people may think about finding the areas of different shapes, and it also showed me how to make it easier on myself when I'm finding the area of different shapes.

I’m excited by the potential that students from around the world can engage in mathematical discourse. Imagine the classroom from the inner city talking with the classroom from the suburbs, or the independent learner from Mumbai talking with the google searcher from Atlanta. Imagine all of those learners discussing mathematics together.

[klr]

Peer Work or Curated Work?

Last week we went to a school with a modified task. In the full classroom-version of the task, the set of generated student work is leveraged by the teacher to develop, synthesize and connect student conceptions and math concepts.

In other words, the students contribute work, the teacher expertly stirs it together, and supplies rich, combined ideas back to the class for them to digest.

Independent learners online do not have a human teacher to stir their work and do not see the work of their peers. What if they could? Is more valuable to see authentic peer work, potentially opening peer-learning avenues, or crafted/curated work that is fine tuned by the problem author to prompt new ideas?

On a sad note before I continue, the classroom Square Areas task was developed in part by Malcolm Swan of the University of Nottingham as a part of the MARS project (Math Assessment Resource Service). Dr. Swan passed away this week, but his contributions to the field of mathematics education will continue to have enormous impact.

The students in this class were largely not successful at engaging with the task as presented. In a strict sense, there was only one right answer. Even worse: there were eight more submissions that were entirely blank. (The students were given approximately five minutes.)

What opportunities exist to move each and every student’s thinking forward?

In the classroom case, Smith and Stein present Five Practices to Orchestrate Productive Mathematical Discussions:

1. Anticipate student strategies and pre-conceptions before the task. 2. Monitor student work as the task is being performed, noting anything unanticipated. 3. Select student work (for discussion) that may provide material for discussion. 4. Sequence the student work to be displayed in a way that prompts contrast, comparison and synthesis. 5. Connect student work, student ideas, and larger mathematical structures by facilitating a student whole class discussion.

In the online case, with no expert teacher present, we want to support and scaffold meaningful learning that comes from analyzing the reasoning of others and looking for structure. Computers can’t expertly select and sequence student work. What if we put all of the work in front of the learners themselves? 

Cordelia, Ulysses, Adam, Biron, and Diana all drew at least one additional triangle around the tilted square. Could each of them recognize their strategy being attempted by their peers? Could Emelia and Quintus notice their area formulas coming in handy with their peers work on shapes? What might Helena and Octavia talk about regarding squares and square roots?

During this round of the trial, the students were shown a random pair of work samples from their peers. 

But no pair of work in the trial would be quite as intentionally provocative as work like the MARS supplied curated samples of Kate and Simon (note: the parameters of the problem are slightly different):

Why not just supply online students these curated work samples in their flow? Entire curricula have been built around leveraging this kind of analysis.

The peer work case has another potential benefit though: we can aim for productive mathematical discussion. Students can receive feedback in response to their work.

Say we show Biron the spread of all the work samples not just a random pair. Instruct him to card sort the solutions based on “similarity” or merely select a single group for similarity/interesting-ness. Biron can then write about why he grouped the solutions the way he did and that writing can be transmitted to all of the members of his sorted group. Perhaps then we have Biron attempt to “use your group’s methods” to help him revise his own solution.

Then we can show Biron’s revised solution to the group that helped inspire him. Hey, and it’s the internet, lets show the solution develop over time!

We want to move the online-learner-Birons of the world to the point where they can engage with rich tasks, produce rich work, and partake in an online mathematical conversation. Next up for us: testing some hypotheses around getting students involved in these conversations.

Discuss this post on Reddit.

[klr]

Game designers vs. education researchers on unguided instruction

One strange consequence of our interdisciplinary approach to research is that we’re substantially influenced by both academic educational research and also video game design.

These fields often appear to be talking past each other—which is a shame because they’re exploring many of the same questions, though often not phrased the same way.

One key point of debate in both fields: exactly how much explicit guidance should a student/player get in an activity?

In The Witness, players learn intricate game mechanics through a carefully-scaffolded series of puzzles. At first, there might be only one path through the puzzle, forcing the player to connect a particular symbol to the properties of that path. A second puzzle in the sequence might offer a few possibilities, allowing players to confirm or refute their theories about the puzzle’s rules. From there, things escalate quickly—all without words.

There’s a whole subgenre of celebrated games that relish in their reticence. In this talk, “Vow of Silence,” Hamish Todd deconstructs the design decisions in these games and urges his students to eschew tutorials and explanations in their designs. Instead, to preserve the joy of discovery, they should carefully structure their activities so that players will learn what they need to learn through play.

Meanwhile, over in education research, one top citation has the foreboding title “Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based experiential and inquiry-based teaching.” The authors review the experimental literature and find, on balance, that direct instruction reliably delivers better test scores than minimally-guided alternatives.

There’s plenty to quibble with in this paper (and there are plenty of rebuttals). For instance, it focuses on total novices—maybe discovery-based learning triumphs with more expertise. From game design, we’ve learned that we can’t just naively remove all explicit guidance: we must carefully mold players’ interactions to implicitly provide that guidance. Maybe the minimally-guided experiments in that paper didn’t do that.

And so on.

I shared this paper at a meetup of educational game developers at this year’s Game Developer Conference, and they looked at me like I was from another planet. Alex Peake suggested: okay, fine, maybe the test scores are better with heavy guidance, but who cares? As a game designer, what I care about is: do they finish the game? Are they going to play my next one?

The game developers are optimizing for joy, empowerment, discovery. Yes, they’d like players to thoroughly understand the game’s mechanics, but that’s a secondary goal. The game designers are not asking the same question as the education researchers.

For example, in The Witness, players can skip several whole areas of the game and still reach its ending. This escape valve allows a frustrated player to proceed to an area they might find more interesting—prioritizing joy, empowerment, and discovery over completeness. Maybe they’ll return to the incomplete areas later; after all, the game is cleverly designed so that players will absolutely know they skipped some spots. Perhaps that’s pressure enough.

This idea seems to connect to one Jenova Chen explored in his master’s thesis: games should try to keep players in “flow,” balancing challenge and ability. Jenova argued that we should give players more fluid control of the challenge they take on, so that they can manage their own position relative to their own intellectual “sweet spot.”

Maybe the same idea applies for players steering towards their emotional “sweet spots.” If we minimize mandatory explicit guidance, we let player decide how much they’d like to pursue the joy of discovery. Maybe some players will choose to access a tutorial before taking control in an activity. That’s fine. This decision is more about emotional investment and curiosity than it is about challenge—a different kind of “flow” to maintain.

What happens when instructional design asks the same question as game design? I think Chaim Gingold’s Earth Primer is our best answer to date.

In this digital book, each bifold features an interactive geological simulation on one side, and explanatory prompts on the other side. According to their own emotional flow, students can choose to engage with the explicit questions the book poses, or they can explore the simulations freely themselves. They’re in control, guided by their own sense of joy and discovery.

Perhaps not everyone who reads the book would do as well on a geology test afterwards as they would if they’d been given a lecture… but I bet they’re much more likely to read Chaim’s next book. When and how should we choose to optimize for that in our designs instead of for test scores?

Discuss this post on Reddit.

Hmelo-Silver, C. E., Duncan, R. G., & Chinn, C. A. (2007). Scaffolding and achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark (2006). Educational psychologist, 42(2), 99-107.

Kuhn, D. (2007). Is direct instruction an answer to the right question?. Educational psychologist, 42(2), 109-113.

Kirschner, P. A., Sweller, J., & Clark, R. E. (2006). Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educational psychologist, 41(2), 75-86.

Schmidt, H. G., Loyens, S. M., Van Gog, T., & Paas, F. (2007). Problem-based learning is compatible with human cognitive architecture: Commentary on Kirschner, Sweller, and Clark (2006). Educational psychologist, 42(2), 91-97.

[klr]

Safely showing students how others see their work

We’re exploring a student-driven engine for supporting open-ended problem solving. This is the theme underlying many variations:

A student does some open-ended task.

They extend their understanding through a task involving peers’ earlier open-ended responses—maybe elaborating, synthesizing, or reacting.

That task generates either direct feedback for the original authors, or else indirect fodder for a follow-up task involving their peer’s use of their work.

The third step is particularly tricky because, as we all know, people are awful on the internet. Even without anonymity, bullying is a problem in schools. If we’re only asking students to grade each others’ work, we can handle misbehavior by looking for students whose peer grades rarely agree with others’… but we’d like students to produce open-ended responses to their peers’ open-ended work! Ideally, those responses won’t have to be evaluative: other formats may better stimulate further thought.

How might we help students benefit from rich reactions to their work while avoiding abuse?

One approach is to make the communication channel much narrower. For instance, we could reflect a high-level emoji reaction back to students from their peers. Interaction can still be fairly rich this way, as seen in Journey’s wordless collaborations.

We could impose moderation or involve teachers in approving students’ communications, but that would slow down the feedback loop substantially. Civil partially shifts moderation responsibility to users, asking internet commenters to rate the civility of others’ responses—and their own—before allowing them to leave a comment.

Is there a middle ground? A channel wide enough to inspire plenty of follow-up thought, but narrow enough to need less moderation? We’ve discussed a few ideas so far.

Watching a student extend your work

In math, we might show a student a peer’s strategy, then ask them to solve a new variant of the problem. In the humanities, we might show a student a peer’s essay beside their own, then ask them to draw lines between all the places they and their peer were making the same argument.

Then we can show that work back to the original peer. It may even be interesting to see the literal replay. Seeing another student understand and extend your work may itself prompt new thoughts.

Did your peer deploy your strategy exactly the way you did? Maybe they took a shortcut you didn’t think of!

Did your peer have a different angle on the same argument you were making? Did they arrange the arguments in a different order? Does that order flow better? What about the arguments they used which you didn’t use?

Relationships and connections

Arrangements and rearrangements can supply rich fodder for follow-up thought over a channel narrow enough to avoid moderation risk.

For instance, we’ve written about asking students how similar two peers’ responses are to each other. We can establish clusters of student work from that data or by directly asking students to sort each other’s work into clusters.

Once we have those clusters, we can show students their work as arranged in context of peers’ work. Do they see why others have marked certain work as similar to their own? Do they disagree with the arrangements? Can they see subgroups in the clusters?

We can also ask students to establish orderings within their peers’ work. For instance, we might jumble up a student essay’s sentences and ask a peer to arrange them sensibly. What does the original author think of the new arrangement? We can even make the system ask that question only if the peer’s arrangement is different from the original.

Or we could erase all the quotes from a history essay but leave the surrounding text… then ask a student to find the passages in the primary sources which might belong in the quoted regions. What does the original author think of the substitutions? Do they provide another angle on the same argument?

Contextual reactions

In addition to allowing students to apply emoji to an entire piece of student work, we could give them a curated supply of emoji stickers to place within the student’s work, where the feel it might apply. Maybe a particularly strong argument gets a 🔥 sticker. Or in a math proof, students could put the 😎 sticker on a specific step. Besides being interesting feedback for students, data at this granularity could also help us drive more interesting rich tasks in the future.

We’ve also explored giving students a set of highlighters where each color means something specific. For instance, we might ask a student to highlight an essay in blue wherever evidence is being used, in purple wherever an opinion is stated, and in yellow wherever an opposing argument is rebutted. The original author might be surprised to see a surplus of purple or a lack of yellow—a great opportunity for revision.

We’re continuing to generate more ideas here, but we’re also narrowing down on a small subset of our concepts for a live prototype soon. Time to start building!

Discuss this post on Reddit.

[klr]

Will we type math still in the future?

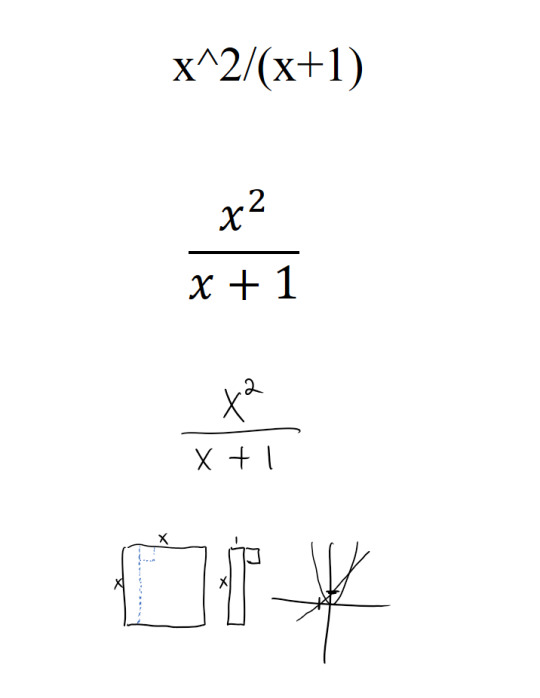
Typing mathematics expressions is hard. The standard formats for fractions or exponents require extra keystrokes or an extra layer of software, or for perfection, the knowledge of LaTeX. But try expressing any kind of rough thought or diagram and you’ll reach for your paper notebook.

With pen and paper, we have much greater freedom of how to express our thoughts. Software exists, shortcut your handwritten math expressions to established norms, (example 1, example 2) but what about capturing the richer more free-form expression of general thought?

Will the availability of pen input tablets grow to the point where they are commonplace in schools? Things like the Surface or iPad or Wacom are too expensive now for mass adoption, but old Galaxy Note devices are nearing the cost of the ubiquitous TI-84.

Teacher tools such as Desmos (pictured above) and Formative allow students to sketch and draw to various degrees. But using a finger on a phone or trackpad doesn’t give you the precision of a pen.

The best input experiences come with steep price tags but allow much of what can be done with paper along with some tech affordances. For example, cut and paste or undo/redo can be very useful to someone writing or drawing on a tablet.

But additionally, how about the advantages we have upon receiving this data? Such as the ability to playback the student’s freeform expression? Compare glancing at the final product image for 7 seconds vs the 7 second process timelapse:

GIF:

(high quality version of above animation)

Education companies are already able to do cool things with the finger sketches...

Can we fully merge the advantages of technology with the freedom of pen and paper? The future might be closer and cheaper than it first appeared! 

Used Galaxy Note 4:

$30 Huion USB input pad:

Comments @ reddit.com/r/klr

[klr]

How cool is your math?

At advanced levels of math, people call certain solutions “elegant,” “beautiful,” or even “rad.” Some Spanish-speaking mathematicians call a clever solution a “cabezazo” – the same word used to describe a beautiful header goal in soccer. People develop a taste in math. Problems at this level tend to be rich in possibility; they can be approached and solved in a variety of creative ways. 

At the same time, it seems too rare that students in grade school get to try a rich mathematical task and take a step back to compare different strategies for solving a problem – let alone decide if they think a solution is “cool.” 

Yesterday Andy, Scott and I had a chance to chat with Professor Judith Kysh at SFSU about our thinking thus far in the universe of open-ended responses. We mentioned having students compare their responses and strategies to those of others, and how we think this might help them reflect on their own strategy and maybe even understand the problem from a different angle, while providing us with data to help us cluster solution-types.

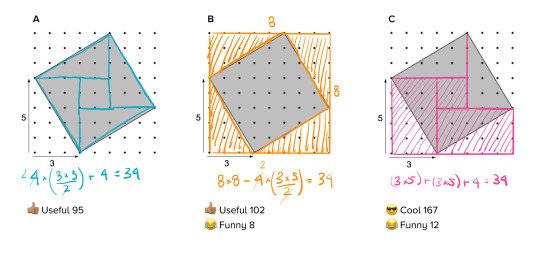
Dr. Kysh brought up an exercise she learned from some visiting Japanese educators. They had each student rank all the solutions that had been shared within the class, from least to most favorite. This meant that not only were the students exposed to a wide variety of strategies to consider – they also had to decide on their affinity to various strategies. Note: all strategies discussed led to a correct solution, so this was not about being right or wrong!

The exercise of publicly force-ranking people’s work might be difficult for some people to stomach, but in our work we have the advantage of being able to anonymize authorship and potentially circumvent some of the social status issues. What if, after a student submits their own solution, we could show a student a diverse sample of solutions drawn from our past learners, and let them sort from their least to most favorite?

Or… here’s another idea we toyed with: what if students could see alternative solutions to a problem and mark them as “cool!” with an emoji? Would you be proud if 67 people thought your solution was “cool” … or even “helpful” or “funny”? Might more people in the world start to think of solutions as “cool” and strive to find them? Might this extend beyond math?

Our day at SFSU was inspiring and there are many more stories to come; I hope we have a chance to share those with you soon.

[klr]

Rich tasks crowdsourcing data for more rich tasks

…or: how we evaded a gnarly machine learning problem and found an interesting task for students to do along the way!

Some background

If students are going to “construct viable arguments and critique the reasoning of others,” they’ll need to see the reasoning of others! Whose reasoning should we show? In what order? With what structure?

When orchestrating discussions in class, great educators carefully select and sequence [Stein] student responses to share in whole-class discussions, lightly scaffolding the class as they connect the responses’ ideas.

What about outside of class—when doing homework? When studying for a test? We’re excited about digitally fostering rich questions with open-ended responses in these contexts, too.

Multiple-choice activities can at least inform the student if they’re right or wrong, but feedback is subtle and multidimensional with richer tasks. Besides: evaluative feedback alone won’t help a student develop intellectual autonomy in the way great classroom discussion does [Yackel and Cobb].

When students wrestle with rich problems outside class, they have to push on their own understanding. Unfortunately, even with highly-structured reflection scaffolds, students who can effectively push on their own understanding are likely already high performers [Lin].

We’re exploring the idea of rich digital activities that push on student understanding by confronting students with their peers’ work—not necessarily to critique their reasoning, but to provide a scaffold for students to form new connections and deeper conceptions.

Bringing an activity home

Michael Pershan demonstrated a variety of student strategies in this activity:

In a classroom, a teacher might select and sequence student work to strategically facilitate whole-class discussion. What if a student tackles this activity outside class?

This might be an interesting follow-up question:

What’s more: we can then share the student’s explanation of strategies A and B back with their original student authors. We can ask those students if their peer’s explanation matches how they think about their own strategy—yet another opportunity for decentering, per Piaget.

[Aside: there are deep problems, of course, in exposing students to freeform responses from others online; we respect the dangers here and are investigating mitigations we’ll discuss another time.]

This activity now has competing requirements:

Ensure each completed strategy gets a response from another student.

Ensure strategy A and strategy B are actually different!

We can solve requirement 2 by carefully curating the student strategies we show, but then we won’t satisfy requirement 1. If we randomly select student strategies to hit #1, we’ll miss #2.

In conversation with Scott on this tension last week, I started talking about how we could start training a machine learning system to classify these kinds of student diagrams, ticking off various challenges we’d have to overcome.

Scott proposed a much more elegant solution: have the students classify strategies—it’s a mathematically interesting task anyway! Before the detailed comparison activity above, we can present this less demanding warmup:

Implications

Lots of variants are possible here. We could ask them to sort a set of strategies into clusters, we could give them a continuous difference input, etc. But using student responses, we can reliably show the student a pair of differing strategies in the subsequent activity. If we want to be very confident, we can require that multiple students have marked the pair of strategies as different. No perilous machine learning here.

This idea has another fascinating upshot: we can use this difference information to surface patterns of student work to teachers! If students have marked strategy A as being similar to strategy B, and strategy B as similar to strategy C, we have a possible cluster of related work.

We can lay out student work on a plane, using the similarity metric to drive a force-directed layout. Teachers could quickly see common strategies, or student strategies which aren’t similar to any other student strategy, and so on.

This one warmup task functions in three ways at once:

The system gets a big pool of differing pairs of strategies for the follow-up task.

The student gets a mathematically-interesting activity involving others’ work.

The teacher (and researcher!) get macro-level insights about student work.

And bonus: it’s easy for me to imagine using the same technique for activities in the humanities.

Besides asking about similarity, what other tasks might function in this way? For instance, we could ask students to apply tags—e.g. to arguments made about feudalism’s impact on medieval Europe. Lots to explore!

Discuss this post on Reddit.

Lin, X., Hmelo, C., Kinzer, C. K., & Secules, T. J. (1999). Designing technology to support reflection. Educational Technology Research and Development, 47(3), 43–62. [PDF]

Stein, M. K., Engle, R. A., Smith, M. S., & Hughes, E. K. (2008). Orchestrating Productive Mathematical Discussions: Five Practices for Helping Teachers Move Beyond Show and Tell. Mathematical Thinking and Learning, 10(4), 313–340. [PDF]

Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27(4), 458. [PDF]

[klr]

Feedback is a gift

Without feedback, we’d all be operating in a vacuum, completely unaware of the ramifications of our actions. Imagine trying to learn something brand new without being able to receive feedback.

Feedback is talked about in forums of leadership, business, parenting, teaching, design, and much, much more. It helps us get better at what we do, and get better as people, both as givers and receivers. 

Can you think back to a moment you received feedback that changed your behavior or thinking? What do you remember about the situation and how you felt? What made that feedback stick?

In our long-term research group, we want to move beyond the duality of right or wrong, and into the landscape of open-ended response. Can we react to these responses in a way that cultivates deeper understanding and develops stronger meta-cognitive skills?

When I’ve had this conversation casually, I’ve observed many people assume we want to focus on better machine-grading for essays. Grading is a form of summative feedback, focused on an outcome at the end of a class or lesson.

Instead, we’d like to consider formative feedback, which is used on an ongoing basis to help everyone in a situation identify how they might improve what they are going to do next. I’m deliberately generalizing these terms beyond the traditional educational context because I find they apply anywhere. Have you ever tried to give somebody feedback to help you interact better in the future (formative), and had them interpret it as a personal judgment (summative)? Have you ever received a grade or performance review (summative) and wished that instead you’d received more advice about how to improve your performance along the way (formative)?

Open-ended response is powerful because it can explicitly reflect actual student thought. This applies not only in writing exercises for the humanities, but also in math. For example, Desmos activity builder’s question screen is designed to allow students to share their thinking with their teacher, and potentially with each other, during class. Hand-written student work on paper lets teachers see students’ step-by-step thinking. The question is: how can we, in software, provide response to that thought?

Below I’ve sketched some ways in which we can collect or display feedback to open-response questions within the user interface. (Yes, please read the handwriting.)

Note that many of these could be used in combination with each other. Forms such as freehand markup capture a kind of richness that’s missing in typed text. Voice and video recording start to capture intonation and non-verbal expression.

Within the context of feedback delivered via software, we’re also considering:

Who the source of feedback is:

Learner to self (self-reflection)

Peers

Teacher or coach

What the feedback is focused on:

The task output

The approach or process

The metacognition or self-regulation of the learner

The feedback that’s been received (i.e. feedback on feedback)

How we can structurally support:

Useful timing of feedback

Content of feedback that’s appropriate for the learner and the task

Iterative creative process

More background on feedback

As part of the background reading for this exercise, we’ve looked at Valerie J. Shute’s paper Focus on Formative Feedback, a meta-analysis of educational research literature on formative feedback. Outside the realm of software, many aspects of feedback have been studied for effectiveness, including:

Specificity. The level of information presented in feedback messages.

Directive vs. facilitative. Directive feedback tells the learner what to do or fix, facilitative feedback provides comments or suggestions to guide the receiver’s own revision or conceptualization.

Verification. Confirms whether an answer or behavior is correct. This is further divided into:

Explicit. e.g. a checkmark

Implicit. e.g. does an interaction with the learning environment yield what the learner expects, without explicit external intervention? As an example, Shute uses a learner’s actions within a computer-based simulation.

Elaboration. More informal aspects of feedback that provide cues beyond what’s provided in verification. E.g. offering more information on the topic or other examples

Complexity and length.

Goal-directedness. Goal-directed feedback gives learners information about progress toward a desired goal or goals, rather than on an individual action.

Scaffolding. Scaffolded feedback changes appropriately for different stages of the learning process.

Timing

Delayed vs. immediate.

Timely. On time to be applied in a repeat situation.

Regular. Delivered according to a schedule.

Continuous. We’d argue that continuous feedback is another kind of timing, not included in Shute’s survey. It refers to interactions such as the sliders in this essay by Bret Victor, and is one of the most fascinating for us, since it can transcend being feedback and serve as a way of discovering unexpected results.

Norm-referenced vs. self-referenced. Norm-referenced feedback compares the individual’s performance to that of others. Self-referenced feedback compares their performance relative to markers of their own ability.

Positive vs. negative. Praise, encouragement, discouragement, etc.

Feedback resulted in various levels of effectiveness depending on aspects of the learner:

Learner level. High-achieving vs. low-achieving, prior knowledge or skills.

Response certitude. The learner’s level of certainty in their response.

Goal orientation. Learning orientation is characterized by a fundamental belief that intelligence is malleable and a desire to keep learning (a.k.a. “growth mindset”). Performance orientation is characterized by a fundamental belief that intelligence is fixed and a desire to demonstrate one’s competence to others.

Motivation. What the learner is motivated by and how much.

Meta-cognitive skill. How much the learner is able to self-regulate their own approach to learning.

And of course feedback effectiveness depended on aspects of the task or activity:

Rote, memory, procedural vs. concept-formation, transfer. Rote, memory or procedural tasks could be categorized as needing “efficient thinking”, since they tend to be limited and predictable. Tasks requiring deeper conceptual understanding, or the transfer of understanding to a new context, could be categorized as requiring “innovative thinking”, since they are less predictable in nature. (More on innovative vs. efficient thinking here)

Simple vs. complex.

Physical vs. cognitive.

Shute also noticed that, perhaps unsurprisingly, physical context mattered in research outcomes: classroom and lab settings had different results in studies of feedback timing.

You might be wondering: If people have investigated all these aspects of feedback, can they just tell us what works? There’s a wide variety of conclusions and degrees of conclusiveness. None of the variables operate in isolation. And worse, the most well-intentioned feedback can have both positive and negative effects, so it needs to be executed with care. Having said that, Shute does include a summary table of recommendations for effective feedback starting on page 177.

So yeah, there are a lot of variables, which makes for a pretty complex multi-dimensional space of possibilities. Feedback is complicated.

I’d like to add some other variables that aren’t mentioned in depth within the Shute paper:

Perceived credibility of the source of feedback.

Relationship to source.

Number of sources.

Consensus among multiple sources.

Culture of learner or environment. Different cultures or environments make for different expectations around feedback.

Self-esteem of learner.

Mood and health. This includes blood sugar levels, hydration, levels of rest, etc. for both giver and receiver. (Shute does touch on this in “future research”.)

Medium. What medium is the feedback delivered in; e.g., verbal, written, delivered in person, via a computer, etc. In person, people can communicate non-verbally. Intonation, context, and body-language are difficult to transmit via digital text – that’s why we’re hunting for richer ways to use the digital medium.

In this day and age, we’re particularly interested in open-ended responses as opening the door to creativity, dialogue, and most importantly: critical thinking. We hope to experiment with a few building blocks for formative feedback that are interactive and configurable. Stay tuned!

[klr]

Letting Students Be Wrong

I observed an 8th grade class recently. The students were working in groups on tasks related to the Pythagorean theorem. As is often the case with formulas, the buzz of the room centered on correct application rather than deeper meaning. However, the teacher chose the task (via MARS) because it was designed to slow students down by not asking repetitively structured exercises; instead, students may be presented with new angles of approach with successive problems. I decided to sit in with a group which had just found “c=15” for the “length FE”. I’ll call the two girls Megan and Erica, this is my recollection of our conversation. 

“Does the Pythagorean Theorem always work?” Megan: yes. Erica: no.

Introducing myself, I ask, “ok, I see you have 15 for that triangle. What does that mean, though? Why is it 15?” Megan begins to give a procedural walkthrough of using the Pythagorean theorem but I attempt to redirect by approving the calculations. Then, “does the Pythagorean theorem always work?” Simultaneously, Megan says yes, Erica says no.            [M is Megan, E is Erica, S is Scott]            M: yes            E: no            S: What about for another triangle? [clarifying my meaning of ‘always’] If I draw this, how long is the dashed line?

           M: 15 still.            S: how do you know?            M: well because that’s still c, and you take c squared and it equals 9 squared plus 12 squared…            S: Ok, so with two sides 9 and 12, we can’t make the other side bigger? [Erica begins to look concerned but Megan may feel very confident with her calculations which I’ve already validated, so she continues to stick with her answer.]            M: you could make a side longer, like 10. [pointing to the 9]            S: [I draw] ok so this length is greater than 15?            M and E: yeah. [Erica feels more on solid ground here]            S: ok well can we make the length any shorter? [while this is logically equivalent to asking about making things longer it is not pedagogically equivalent]            S: if I cloooose this triangle [I mime with my hands folding the legs of 9 and 12 inward] what is this dashed length?

           E: hmm ya its shorter            M: it’s still c, it’s still 15.            [At this point it was vital for my reactions to be unreadable. I need to listen to their reasoning and understanding, so I must be intentional with which information I validate and introduce. Students are motivated to not be “wrong” for social and academic reasons. But I need to let them be “wrong” to find out what they are right about.]            E: umm… [she trails off]            S: ok one more drawing. What if I close that ‘door’ all the way? [I close my hands together then draw]

           M: that’s not a triangle anymore.            E: its three.            M: its 180.            S: oh 180, do you mean the angle?            M: yeah a flat—straight angle is 180. [this kind of statement and the tone of her voice make me think of this knowledge as fact-recall. Despite applying the knowledge of straight angles to this situation, it was in answering a different question, much like the way she uses the knowledge of the Pythagorean theorem in places is doesn’t quite apply.]            S: how about the length, from here to here?            E: that’s three. Because from 9 to 12 is three.            S: shorter than 15 then, yes?            E: yeah.            M: yeah… but it’s not a triangle anymore.

At this point, the teacher had to interrupt the class as the period was almost over. I did not get the chance to dig in deeper with Megan and Erica. Megan appears to have some misconceptions regarding length and the applicability of formulas in general, or the Pythagorean theorem specifically. Erica was quieter but followed my line of questioning more directly and has connected concepts of length to the labels on the triangles.

Megan does have productive knowledge that could be successful in answering many questions that could be posed to her. If given a right triangle with the hypotenuse missing, I’d have every confidence that Megan would be able to find the number for the third side. Her knowledge of the vocabulary “straight angle” also makes me wonder if she finds it productive to memorize. But the most interesting evidence of Megan’s understanding is that she quickly proposed a hypothetical way to increase the length of the third side of a triangle [change one of the lengths to be one unit longer]. I believe Megan thinks about triangles as having the property of a trio of numbers, one for each side. To make lengths bigger you have to make other lengths bigger. But she has not fully connected how angles and side lengths relate.

This means a justification that the Pythagorean theorem “only works for right triangles” might not resolve her misconceptions regarding its application. It might be an additional fact she learns along with the definition of straight angle. But this fact may not fit together into a coherent system in her mind. In contrast, Erica is perturbed by some of Megan’s answers about the lengths, but couldn’t bring herself to fully speak out until she was on entirely solid ground in the last example. It could be the precise “3” length gave her the confidence to make her argument.

It would have been interesting to have this disagreement brought to light for all the students to engage with. Erica can’t quite make her point yet, but other students might be able to assist. And still others might be on Megan’s side. During this discussion, the concept of angle would come up. Students might be able to connect it back to earlier lessons on the triangle inequality. Megan’s trio of sides knowledge does hold water in a certain way; side-side-side congruence of triangles means any three lengths determine a triangle (and thus its angles).

In analyzing student “misconceptions” we must be clear about what idea the student truly holds, and how that idea can be useful. We must help the student to develop their ideas by having them draw connections and build abstractions. Science educator Dr. Eugenia Etkina says, “no amount of teaching will destroy the existing [neural] connections. […] So you rewire the paths.” (youtube) Etkina talks of potentially steering the student around the misconception ideas in their heads, but also of activating student ideas at the right times. Veteran math educator Marilyn Burns searches for questions that ask what the student’s response is saying. And in a landmark 1994 paper, Smith, DiSessa and Roschelle concurred that “replacing misconceptions is neither plausible nor always desirable.” Instead of replacing, confronting or removing a misconception, we need to develop and mature the student’s idea. We should let the student be wrong so that we can figure out how they can be right.

Comments on Reddit

Further Reading:

Burns, Marilyn. “Looking at How Students Reason.” Educational Leadership 63, no. 3 (2005): 26–31.  

Shell Centre and Silicon Valley Math Initiative MARS Tasks http://www.mathshell.org/ba_mars.htm

Smith III, John P., Andrea A. Disessa, and Jeremy Roschelle. “Misconceptions Reconceived: A Constructivist Analysis of Knowledge in Transition.” The Journal of the Learning Sciences 3, no. 2 (1994): 115–163.  

[klr]

Surveying the open-ended response landscape

We’ve previously introduced our interest in amplifying open-ended questions: prompts which break out of the radio button and numerical input to invite exploration, reflection, creativity, and depth. Learning technologies often emphasize simple, machine-gradable interactions—which makes the humanities hard to learn at all, and math hard to learn well. Even for questions which lend themselves to single-dimensional answers, great teachers capture and capitalize on all the student thought along the way.

Long-term Research is interested in learning technologies that foster open-ended questions and their open-ended answers. That prompt is too big to attack directly, so we’re understanding the space and its opportunities better through user research with teachers and a broad landscape review.

We had some familiarity with commercial products that supported open-ended responses, so we began by surveying prior academic work in the space. The most useful publications were the proceedings of the International Conference on Computer-Supported Collaborative Learning and the ACM Conference on Learning at Scale; the Review of Educational Research, the Journal of Educational Psychology, and the Journal of Educational Computing Research.

Once we’d explored issues and ideas around open-ended responses, we began to see some patterns running through the work. There appeared to be many intersecting axes describing different solutions’ goals in the space. Here’s an excerpt of our axes, with some representative examples (click to expand):

The axes had a nice feedback effect: once we’d read enough to see these structures, we started noticing that we didn’t see much representation in a particular area, so we’d search more deeply there. We continued filling in the examples here until we filled a 7’ x 5’ poster:

Then we stepped back and reviewed what we’d learned as a team, looking for patterns and opportunities. I’ll share a few that we expect are likely to guide our future work here.

Many solutions gave students feedback—whether from peers, teachers, or algorithms—but it seems that less design energy has been focused on fostering revision or reflection on that feedback. Student revision can be a great vector for understanding, so how might we support students in integrating what they’ve learned by revising their own work?

These solutions largely focused on a single subject. We’ve got TurnItIn for grading essays, and Desmos for a few subjects in math. Are there underlying structures in these open-ended responses that we can support across subjects? For example, we’ve got systems which support multiple-choice responses across subject boundaries; can we make systems as flexible and easy to use for more open responses?

Creation is messy. There are some tools which support wild scribblings, but there’s a canyon between them and the blank word processor page. We saw a few projects make tentative steps across this gap, but we’re excited by how we might support students as they move through the entire creative process from scribble-thought to outline to polished submission.

A spell checker gives students rapid feedback on their writing. Our tools now go a bit further, even attempting algorithmic feedback on essay structure. There’s another kind of instant feedback, though: consider Earth Primer’s sandbox or Cantor’s numerical manipulation tools. In these environments, the interactions themselves continuously communicate with the student while they manipulate objects. Cantor’s resize handle delivers a very specific scaffolded feedback. Can this idea be generalized? Applied to new subjects?

Finally: so many of the tools in this space are focused on substituting for preexisting classroom experiences online. This brings to mind Ruben Puentedura’s model for technology’s impact on teaching and learning:

A word processor initially substitutes for a sheet of paper. With an integrated dictionary and collaborative commenting features, it augments that original experience. But are we overfixating on existing media, ignoring opportunities to modify or redesign what it means for a student form their ideas, express them, receive feedback, and iterate? Are we hill-climbing instead of finding the next hill?

Next up for us: generative ideation based on what we’ve learned during this landscape survey.

[klr]

Metagames in Math Lessons

You play rock, paper, scissors against your friend. He always shows rock and now you start thinking about using his pattern against him-- now you’re playing the metagame.

A metagame takes place outside the supposed scope of a game.

Sometimes a metagame refers to the overt structure outside of the main gameplay. Angry Birds is a game of slingshotting birds, but a metagame is the progression through the levels via collecting stars and unlocking pathways.

But the metagame also refers to the more subtle structure discovered as people attempt to “solve” the game [1]. In our basic rock paper scissors example, the metagame involves trying to figure how your opponent is likely to play so that you can take advantage of it. For a more complex example, take baseball. A metagame of scouting players not only affects who is on the team but has led to changes in how the game is played. With the motivation of competition, deeper structures are sought in the process of attempting to solve the game.

What are the metagames of math class?

Can we leverage them such that the search for deep structure of a metagame becomes entangled with the search for deep structure in mathematics?

[1] more on this below the fold.

Students are great at playing metagames

A teacher asks the class, "if x+5=8, what is x?" The students are now doing calculations -- but not (only) on x+5=8. They are balancing the social and academic costs/benefits of speaking up or raising their hand. In that ruleset, one common strategy might be to tentatively raise your hand hoping to gain the benefit of the appearance of knowing while not necessarily being called on. Another might be to respond with a burst of tentative answers "3? No -3 ya 3. 2. 3." while studying the subtle reactions of the teacher to receive information on which is correct. See: Clever Hans. But students also pick up what subtle notions of what counts as "different" or "sophisticated" or even what counts as acceptable line of reasoning from how the classroom socially and logistically operates. "These normative understandings are continually regenerated and modified by the students and teacher through their ongoing interactions." (Yackel & Cobb, Kamii, Voigt)

Learning from metagames

The upside of all this is that students are motivated and able to learn complex, deep, and subtle concepts via metagaming. Yackel and Cobb explicitly recommend the teachers attend to that space of learning, the acquisition of sociomathematical norms.

Game designer David Sirlin pays a lot of attention to how solvable a game is. For example, tic-tac-toe is solved because there is a strategy that guarantees victory: a pure solution. Player 1 must only follow the procedure to win. But if player 1 is given the procedure they learn nothing about how the game works. It is in the search for the solution that learning occurs. Sirlin designs his games to be as unsolvable as possible.

Constance Kamii has designed learning experiences that directly put students in games that engage one set of mathematical concepts while the metagame exploration engages another math concept. As students play and gain experience, they build ideas in the metagame about how to solve the game. Because Kamii has entangled mathematical concept and practice at both levels, the games have a lot of educational power. 

Motivations and Metagames

A student might be motivated to get high grades, achieve high social status, comply with parent or other authority wishes, resolve curiosities or plainly seek knowledge. These perhaps suggest large "metagame of life" but that is outside of my focus. Instead those items I'll broadly categorize as motivations that are accessed by various metagames in the classroom. Just as we dig into a rock-paper-scissors metagame analysis by assuming a desire to win, we'll dig into math classroom metagames by assuming some set of motivations.

First some low-math-entanglement metagames:

- Perhaps a familiar metagame are riddle worksheets. Students do a drill sheet while completing a riddle/joke. Sample This is of course not leveraging a lot of mathematical thought but I still call it a metagame because the students will eventually balance their math skills against some sort of "phrase completion" logic that will serve to provide or check answers for them.

- Some teachers might explicitly say the goal is to be accurate. This is separate from the motivation but it is trying to utilize it. I feel this is an attempt to wrap the math tightly to its most entangled state: surely if the goal is to do math then they'll learn math in the meta as well! No: it short circuits because there is no second level of information to operate in.

- Goals around achieving grade points or non-grade-linked stickers/badges/rewards do encourage gaming. Highly motivated students will find ways to maximize their grade or badges for minimum effort. They might find ways to socially encourage higher grades, or align themselves to expected behaviors from the teacher. Now sometimes these things are desired and sometimes they're not. But they aren't necessarily mathematical learning experiences.

Things that are better about entangling math:

- Sequenced problems suggest incremental changes of strategy to students without directly giving procedures. While this isn't extremely powerful, I feel it illustrates that the student operating on the set of the problems can use that information to attack a single problem. And if that set of problems is constructed with intent, the information in the metagame (the set) can reveal deeper mathematical structure.

- We already briefly discussed Kamii's games but here's another one:

Finally (but not exhaustively), “How many ways?” Sample: Traincar numbers . Asking students to find "different" ways engages them with the calculations of each individual way (in the example, arithmetic) while also having the metagame explore combinatoric structures (in the example: arrangements, permutations, exponential growth…).

What metagames do you set up with your students? What metagames do you learn from in your own experiences?

Comments at Reddit

Cazden, C. B. (2001). Classroom discourse: The language of teaching and learning (2nd ed., Vol. 6). Portsmouth, NH: Heinemann.

Kamii, C. (1994). Young children continue to reinvent arithmetic: implications of piaget’s theory (3rd grade). Teachers College Press.

Kamii, C., Lewis, B. A., & Kirkland, L. (2001). Manipulatives: when are they useful? The Journal of Mathematical Behavior, 20(1), 21–31. https://doi.org/10.1016/S0732-3123(01)00059-1

Kato, Y., Honda, M., & Kamii, C. (2006). Lining Up the 5s. Young Children on the Web.

Meyer, D. (2009, December 13). Asilomar #4: Be Less Helpful. Retrieved from http://blog.mrmeyer.com/2009/asilomar-4-be-less-helpful/

Sirlin, D. (2014). Solvability. Retrieved from http://www.sirlin.net/articles/solvability

Voigt, J. (1992). Negotiation of mathematical meaning in classroom proccesses. Quebec, Canada: ICME VII.

Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27(4), 458–477.

Zevenbergen, R. (2000). “Cracking the code” of mathematics classrooms: School success as a function of linguistic, social, and cultural background. In J. Boaler, Multiple perspectives on mathematics teaching and learning (pp. 201–223).