paulspuzzles

[paulspuzzles]

Solution #15

Well, all right, it wasn’t tomorrow.  I was, in fairness, busy with work :).  But yeah, solution below the line as per usual...

So I was thinking a little bit about sums, and alternate product formulas for writing out sums.  The formula for triangle numbers (aka the sum of the first n natural numbers) of course being perhaps one of the most famous formulae of all time:

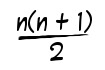
The first few triangle numbers are 1, 3, 6, 10, 15, 21, 28, 36... you might be wondering why I’m bothering to list them, but I’ll be getting to that shortly.

Another formula I was thinking about was the formula for computing perfect numbers.  To recap: a perfect numbers is a numbers whose factors (other than itself) add up to itself.  E.g. 6 = 1 + 2 + 3, 28 = 1 + 2 + 4 + 7 + 14.  There aren’t many perfect numbers, the list starts out 6, 28, 496, 8128 before leaping up to 33,550,336 and then just kinda going crazy from there.

Now the formula for even* perfect numbers is another famous mathsy formula, and is as follows:

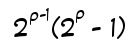
where 2^p - 1 is prime (such prime numbers being called Mersenne primes).  3 (4-1) is prime, and so 6 (2x3) ends up being perfect.  7 (8-1) is prime, so 28 (4x7) ends up being perfect.  Then we skip up to 31 being prime, which leads to 496 (16x31) being perfect, and 127 (128-1) being prime, which leads to 8128 (64x127) being perfect.  Followed by a big ol’ leap to 8191 (8192-1) being prime and 33,550,336 (4096x8191) being perfect.

I’m honestly not sure if I’m spending too much or too little time explaining this stuff but at this point I really just want to get to the galaxy brain moment, which is:

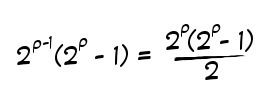
or in other words “hey, the triangle number formula and the perfect number formula look weirdly similar.  what if... what if I just take a factor of ½ out of the perfect number formula?”

A little more arranging gives us:

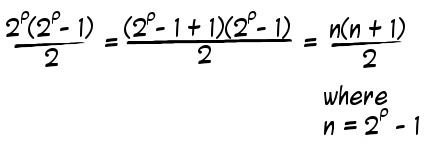
So every even* perfect number is the (corresponding Mersenne prime)th triangle number!  And if you look back at the triangle numbers I listed above, sure enough, there are 6 and 28 bold as brass as the 3rd and 7th triangle numbers.  496 is the 31st triangle number, 8128 is the 127th triangle number, 33,550,336 is the 8191st triangle number, and so on and so forth.

All right.  After all that, back to the actual dang puzzle.  Well, let’s go back to our original definitions of what triangle numbers (adding up consecutive natural numbers) and perfect numbers (adding up factors of a number) involve!  For 6 we get the fascinatingly trivial

1 + 2 + 3 = 1 + 2 + 3

Cancelling down, this just gives us our first term, 0 = 0.

For 28 it gets more fun and was the starting point idea for this puzzle:

1 + 2 + 3 + 4 + 5 + 6 + 7 = 1 + 2 + 4 + 7 + 14

which cancelled down gives us our second term

3 + 5 + 6 = 14

It’s odd to think that this simple sum can be hiding so much behind it!

The third term is the same logic applied to 496, on the LHS we have the sum of the natural numbers from 1 to 31 and on the other side we have the sum of the factors of 496 (other than itself).  And hopefully you’re starting to see why doing this for the fourth term felt nightmarish, and the fifth term was unthinkable!

In some ways this is a kind of barmy puzzle but hey, I had an idea and investigated where it went and something vaguely puzzle-like popped out.  That’s how most of the puzzles on this blog work anyway.  See you in another year or something, I guess.

* An odd perfect number has never been discovered, and it’s a reasonable conjecture that there is no such thing, but it hasn’t been proven. So we’re stuck with having to qualify a lot of statements about perfect numbers with “for any even perfect number”...

[paulspuzzles]

Puzzle #15

Obligatory "It's been a while" statement. You know how it is

Here's a weird puzzle for you. What is the significance of the following sequence of equations?

0 = 0

3 + 5 + 6 = 14

3 + 5 + 6 + 7 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 17 + 18 + 19 + 20 + 21 + 21 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 30 = 62 + 124 + 248

There are more terms, but as you can imagine the fourth term would be absurdly unwieldy to write out and I don't even want to contemplate writing out the fifth term (which in itself might be something of a clue...)

Solution tomorrow, hopefully!

[paulspuzzles]

Solution #14

Oh, I completely forgot I’d posted this.  Guess the solution wasn’t tomorrow after all.

Either way, it’s below the line

The sequence is the smallest numbers that divide by every natural number up to 1, 2, 3, 4, 5... etc. up to 360360 being the smallest number that will divide by every natural number up to 13.  The next three numbers in the sequence are: 360360 (smallest number that divides by every natural number up to 14) 360360 (ditto 15) 720720 (ditto 16)

There are several repeated numbers in the sequence because these numbers are already “covered” somehow - as you might expect, the biggest jumps in the sequence are when a new prime shows up, with smaller jumps being for when another factor of 2 or 3 needs to be added.

The nice repeating digits patterns for 360360 and 720720 come from the fact that 1001 happens to equal 7 x 11 x 13 - as such, any number with digits abcabc is also going to divide by these three numbers.  Since 360 divides by every number up to 15 excluding those three, 360360 is going to be the smallest number that divides by every number up to 15.

Perhaps unsurprisingly, several - though not all - of the numbers in this sequence are on the sequences of superior highly composite numbers and colossally abundant numbers.  I’m not entirely sure what the formal definitions of these numbers mean, but it’s pretty clear that they have a gosh-dang high number of factors.  2, 6, 12, 60, 2520 and 720720 show up on both these lists, as do some of their multiples

Anyone fancy counting in base 720720?

[paulspuzzles]

Puzzle #14

Another sequence puzzle!  Find the next three terms in this sequence: 1 2 6 12 60 60 420 840 2520 2520 27720 27720 360360

Solution tomorrow!

[paulspuzzles]

Not-Puzzle #2

Made this animated proof of Pythagoras’ theorem using the principle of similar triangles:

Based off of 3Blue1Brown’s visualisation for cos² θ + sin² θ = 1 - since that identity is a special case of Pythagoras’ Theorem, I thought I’d generalise it to any right-angled triangle.

Dropping a perpendicular from the right angle lets us split the hypotenuse h into two sections, which I’ve labelled hx and hy here - and the whole equals the sum of the parts.  Checking the angles shows us that we now have three similar right-angled triangles, and ratios for the side lengths of these triangles.  Some rearrangement and substitution gives us Pythagoras’ theorem!

[paulspuzzles]

Solution #13

Solution below the line!

One person (ADEINSATILZEDA0TIL9 on Discord) correctly guessed that the continuation of the pattern was 10, 4π, 16, 20, 8π ... but couldn’t spot the general pattern.  Which is fair, as I say this is both an approximation and a part of maths that... doesn’t actually crop up much in pure maths, and is more of a science/engineering thing!

The pattern drops out by taking the common logarithm (log to the base 10) of each of these terms, and rounding to two decimal places.  The results (all logs in this post to base 10, all figures correct to 2dp): log 2 = 0.30 log 2½ = 0.40 log π = 0.50 log 4 = 0.60 log 5 = 0.70 log 2π = 0.80 log 8 = 0.90

And of course

log 10 = 1.00 log 4π = 1.10 log 16 = 1.20 log 20 = 1.30 log 8π = 1.40

... though the pattern breaks down at log 32 = 1.51 as the errors start to build up!

Some of these are remarkable in how close an approximation they are!  Common log is something I was hardly taught in my maths classes (let’s face it, we only brought logs up at all so that we could use natural log in calculus) and there was something very joyful about spotting these approximate patterns.  I was spurred to research this from watching 3blue1brown’s “Lockdown Math” series, in particular Grant’s video on logarithm fundamentals: https://www.youtube.com/watch?v=cEvgcoyZvB4 log 2 is the heart of all this.  Since 2^10 is so close to 10^3, it does make sense that the common log of 2 would be very close to 3/10.  With 9dp, it reads 0.301029995... exceptionally close to 0.30103 to 5dp.  Which got me thinking about what taking the common log of successive powers of 2 might look like!  Here are the first 33 powers of 2 to 5 decimal places:

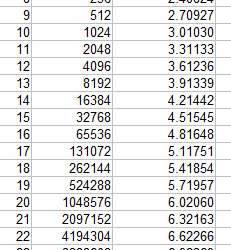
The pattern holds throughout (though past here multiples of three having 3 digits confuses things): the logs of all these successive powers of 2 traces out the three times table!  The first two digits (including the one before the decimal point) are the multiple of 3, the next two are the number itself, and the next two are the multiple of 3 again!  If you can remember your three times table up to 33 x 3 = 99, then you have a quick way to remember the common log of powers of 2 all the way up to 2^33!

It’s even fun to notice things like there being a certain number of multiples of three starting with a certain digit corresponds to the number of powers of 2 with a certain number of digits: there are three two-digit multiples of 3 starting with 2, so there are three three-digit powers of 2.  There are four three-digit multiples of 3 starting with 3 (for the sake of argument here, 1 x 3 = 03), so there are four powers of 2 with four digits!

Common log may have taken a backseat in this era of calculators, but it is still a lot of fun to play around with!

[paulspuzzles]

Puzzle #13

Here’s a puzzle of sorts I came up with the other day.  Consider the following sequence:

2, 2½, π, 4, 5, 2π, 8 What’s the rule for this sequence, and what might the next term be?  As a clue, this sequence is something of an approximation rather than a hard and fast thing.

[paulspuzzles]

Solution #2a

As noted in the original Solution #2, there are many different solutions to this one.  You’ll find some of them below the line.

First let’s start with what I’ll call the five “orthodox” solutions that I found last time.  Credit for finding these is shared between Demerine, Viscardius, crow and myself:

These solutions all have certain things in common: the top three rows are all the same, and use the fact that 6 and 28 are perfect numbers - if you add up the factors of a perfect number other than the number itself, you get the number out.  So if you add up the *reciprocals* of those factors, you get 1.  The bottom row is then the row we play around with to find different ways of filling it up.

From here you can choose to mix things up to find other solutions - so for instance, you can shuffle things around a bit to get results like these:

Though so far we haven’t been super adventurous yet.  So far every solution has left us with five blocks left over.  Can we get a solution that leaves fewer blocks left over?  Or perhaps doesn’t use some of the bigger fraction blocks?  These are actually the same question, since the bigger the leftover fraction blocks, the fewer left over we’ll have.

If you add up all the fractions we have here, you get 71/30, or 2 and 11/30.  Which means we’re going to end up with 11/30 left over no matter what.  But hold on.  11/30 = 1/3 + 1/30, so there should be a solution using all but those pieces...

Yay, it’s thirdless!  You know what else equals 11/30?  1/5 + 1/6... so here’s a solution that doesn’t use the 1/5 block or the 1/6 block. Though the bottom row is a little crammed with small fractions!

Finally, here’s a solution that doesn’t use the quarter block, since we seem to have quite a few ways to make 1/4:

I never noticed any of these back with the original puzzle, because why would I think to try adding up every fraction not in use there?  There were two many of them and adding up 1/19 + 1/23 + 1/29 or whatever just sounds like a headache.  But by restricting myself to just these fractions, it helped me churn out more answers!  Constraints breed creativity, I guess.

See what other solutions you can find!

[paulspuzzles]

Puzzle #2a

Yes, yes it’s been far too long.  And I can’t even promise a new puzzle with this one!  This is, in fact, a rehash of Puzzle #2 (which IMO is easily the best puzzle I’ve ever designed) but with the twist that I've now created a version you can play with yourself! 

I have two versions of the puzzle available: a GIMP .xcf file that you can play around with if you have GIMP or any other art package that can handle .xcf files, or I have a .rar file of all the individual blocks saved as .png files, so you can Open As Layers the whole thing into your art package of choice:

.xcf: https://www.dropbox.com/s/ldwd8gw04yjii54/egyptian%20fractions%20template.xcf?dl=0

.rar with .pngs: https://www.dropbox.com/s/9tb94a9aka5k0db/egyptian%20fractions%20pieces.rar?dl=0

From here you can move each piece around as its own layer and slot them into position (you have to be pixel perfect about it, but hey, that’s part of the fun that exact solutions do exist).

Extra notes below the line:

So you may have noticed there’s been a few changes to the format.  The first obvious one is that our unit fraction pieces are now bars rather than arcs of circles.  I went for bars for a simple reason - I could use it to make each bar length a pixel-perfect size for the fraction I wanted.  Pretty much I found the LCM of the reciprocals of all these fractions, which comes out to 2520, and that became my unit - I made each bar a fraction of that, so the ½ bar is 1280 pixels wide, the 1/3 bar is 840 pixels wide and so on.

It’s an effective system, but it means that the puzzle has been streamlined a lot (which may not be a bad thing, depending on your viewpoint).  Firstly, we’re trying to make four lots of ½ rather than two lots of 1.  This is mostly because I’d’ve had to make the whole thing twice as wide and let’s face it, 1280 pixels fits better on a standard modern monitor than 2520 pixels.

I’ve also left out all the “red herring” fractions - things like the prime unit fractions 1/11 or smaller, or the smaller power of two unit fractions 1/16 and 1/32.  Again, the mechanical reason for this is that for pixel precision they would have made the whole thing larger - 1/16 would have made it twice as big, 1/32 four times as big, and the prime ones even crazier (ah yes, let me make this 31 times bigger to include 1/31).  But at the end of the day, perhaps no red herrings makes for a cleaner puzzle - every fraction you’re presented with is used in at least one solution, and the puzzle still retains the charming aspect that there are many different solutions.  You’ve seen some solutions in action from Puzzle #2 already, but I’ll post some solutions tomorrow anyway.

One last thing - the system I’ve used to label the bars - /2 for 1/2, /3 for 1/3, /4 for 1/4 and so on - is a convention that Robins and Shute (1987) use to denote Egpytian/unit fractions so that a bunch of extra 1s aren’t constantly needed to write them down.  Hope that’s okay.

[paulspuzzles]

Solution #12

As QuantumFizz put it, “Something to do with triangles I incorrectly assume?” - well, except that the assumption was quite correct.  This puzzle involves triangles and, inevitably, Pythagoras’ theorem.  But it also involves another theorem named after a Greek mathematician: Thales.

That’s your one last hint before I reveal the solution!

So Thales’ theorem states that if you have a diameter of a circle (or, well, the straight side of a semicircle), and another point on the circle, then the angle made connecting that point to the two ends of the diameter is always a right angle:

And hey, wouldn’t you know it, that’s a right-angled triangle right there.  Of course, it’s not just one right-angled triangle: it’s three.  Let’s label this up:

So our three right angled triangles here are the big one (x, y, a+1), the left-hand one (a, z, x) and the right hand one (z, 1, y).  We can now use Pythagoras’ theorem to give us three simultaneous equations:

(a+1)² = x² + y² ... 1 x² = a² + z² ......... 2 y² = z² + 1² ......... 3

Let’s sub 2 and 3 into 1 to get:

(a+1)² = a² + z² + z² + 1²

Expanding the bracket and simplifying gets us:

a² + 2a + 1 = a² + 2z² + 1 2a = 2z² a = z² z = √a

Ta-da!  Square roots have always fascinated me - this strange idea of having to work backwards to find an answer, especially given how ugly the answers often are - and any new way to calculate them always gets me excited.

To finish, I’m going to quickly look at a fun special case of this: what if a were 3?  In that case, the circle’s diameter would be 4, its radius 2, and the height of its “square root” line would be √3.  We would have this:

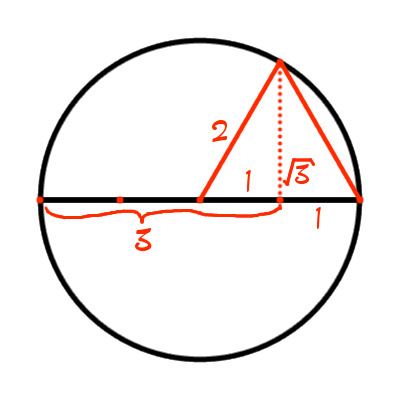
Well would you look at that, it’s our good buddy, the equilateral triangle (See solution 9 for the relationship between the base and perpendicular height of an equilateral triangle)!  So this is one of the options you have when it comes to constructing an equilateral triangle of a given length - have that length be the radius of a circle, make a perpendicular bisector between the centre and edge of the circle, and construct this!

[paulspuzzles]

Puzzle #12

*blows off dust*

Haha, sorry it’s been a while.  And I can’t guarantee it won’t be a long time until the next one of these. But I just learnt something fascinating, and felt I had to share.  I learnt it in this Numberphile video on squaring the circle: https://www.youtube.com/watch?v=CMP9a2J4Bqw

Specifically, the part at the beginning where Dr. James Grime talks about how the Ancient Greeks did their square roots.  Have your line of length a, add a unit length to it, and draw a semicircle on this line of length a+1.

Then the perpendicular line from the semicircle to the end of the a line has length √a!  This astonished me, and I pretty much had to pause the video, sit down and prove it for myself.  And I did!  It felt great, and I wanted to share it.

So there’s your puzzle (well, proof exercise really, but hey!): show that the dotted line here has length √a.  Solution tomorrow.  Note that the comments for the video spoil the solution to the puzzle.

[paulspuzzles]

Solution #11

.Before you click on the “Keep reading” thing for the solution, here’s a bit of a clue: at least one previous puzzle might give a decent hint about what we’re dealing with here.

So, what can we say about the numbers √1, √2, √3 and √4?  Well, for a start we can say that √1 is 1 and √4 is 2.  So with that little simplification, we have:

1, √2, √3, x, 2 2, √3, √2, y, 1

That was easy.  What about √2 and √3?  Where might we have seen those before?

Well, check back with Solution #9, where we talk about the height of an equilateral triangle of side length a being a√3/2, and how this makes for an important relationship in trigonometry - with sin(30°) = cos(60°) = 1/2 and sin(60°) = cos(30°) = √3/2 .

Hmm.  What do we get if we divide both of these sequences through by 2?

1/2, √2/2, √3/2, x/2, 1

1, √3/2, √2/2, y/2, 1/2

Oh hey, there’s 1/2, and there’s √3/2.  And it’s probably worth pointing out that sin(90°) = cos(0°) = 1.  And there’s one other thing we can play with here, which goes back to solution #1: if you have an isosceles right-angled-triangle (i.e., half a square that’s been cut corner-to-corner), then by Pythagoras the length of the hypotenuse ends up being √2 times the length of the sides.

This gives us sin(45°) = cos(45)° = 1/√2 , which if you multiply top and bottom through by √2 gives √2/2.  Hmm.

Let’s deal with the x sequence first and plug in some numbers.

1/2, √2/2, √3/2, x/2, 1 = sin(30°), sin(45°), sin(60°), x/2, sin(90°)

(Or if you prefer, cos(60°), cos(45)°, cos(30°), x/2, cos(0°).  Let’s go with the one that counts up, though).

We’re going up in 15° increments each time, which suggests that x/2 should be sin(75°).  And so, going back to the original sequence, x should be 2.sin(75°).  Which is fine for an answer, but for extra credit you can plug in an exact value for sin(75°) - the two traditional ones being 1/4(√2 + √6) or 1/2.√(2 + √3).

Most people prefer the former exact answer because it doesn’t have that nasty-looking nested root, but let’s have some fun with the latter.  If we double it, the half vanishes and we’re left with √(2 + √3) - our value for x.  And in our original x sequence that becomes:

√1, √2, √3, √(2 + √3), √4

This makes 2 + √3 (about 3.73) our mystery “missing integer” between 3 and 4 - perhaps this is the value of “umpt”!

Let’s go back to y now.  Turning the square roots into expressions in terms of the sine function, we now have:

2.sin(90°), 2.sin(60°), 2.sin(45°), y, 2.sin(30°)

Well it’s no longer as simple as counting on 15° each time.  Maybe this’d be clearer if we used a different unit for angle measuring - radians.

Radians (as you may well already know, so feel free to skip ahead a bit here) are a really cool way of measuring angles - in many ways, they’re the natural unit for measuring angles in, with degrees being a convenient human construct.

If you’ve got a circle radius r, and an arc around the outside of that circle of length Ar, then the angle contained by that arc is A radians.  Since the circumference of a circle is 2πr , that means that a full circle - 360° = is 2π radians.  So 180° is π radians, 90° is π/2 radians, 60° is π/3 radians and so on.  Or in other words:

2.sin(90°), 2.sin(60°), 2.sin(45°), y, 2.sin(30°) 2.sin(π/2), 2.sin(π/3), 2.sin(π/4), y, 2.sin(π/6)

And to fill in that sequence, it’d make sense to make y = 2.sin(π/5) (or if you still want to work in degrees, 2.sin(36°).  Sin(π/5) has an exact value of the lovely looking 1/4.√(10 - 2√5), giving a value of y of 1/2.√(10 - 2√5) (which would make “umpt” (5/2 - √5/2)).

You can of course use radians for the x sequence as well.  75° is 5π/12 radians, so:

2.sin(30°), 2.sin(45°), 2.sin(60°), 2.sin(75°), 2.sin(90°) 2.sin(π/6), 2.sin(π/4), 2.sin(π/3), 2.sin(5π/12) , 2.sin(π/2) 2.sin(2π/12), 2.sin(3π/12), 2.sin(4π/12), 2.sin(5π/12) , 2.sin(6π/12)

And you can see the numbers counting up there as well - 15° is π/12 radians.

And there we have it!  A simple-looking but quite confounding (no-one I asked got it) puzzle about sequences actually being more about geometry and trigonometry.  One of maths’ great strengths is the way it links many different fields together.

[paulspuzzles]

Puzzle #11

Oh boy, it’s been a while.  Sorry, hurt my arm badly the other day and haven’t really been in the right frame of mind for puzzles since.  Arguably I’m not now, since I’m going to be cribbing another one here - this one’s one of my favourites from a book called 50 Per Cent Proof - An Anthology of Mathematical Humour which is mostly just a bunch of maths jokes but does contain a few amusing puzzles as well.

This one, contributed by A. R. Pargeter, is called “Have we missed some integers?” and invites you to complete the following sequences:

√1, √2, √3, x, √4

and

√4, √3, √2, y, √1

Find expressions (or if you want to be daring, exact values) for x and y.  Have fun!  Solution tomorrow.

[paulspuzzles]

Solution #10

Solution behind the “Keep reading” thingy.

So there are a few different things to think about with Tower of Brahma/Hanoi puzzles, but the main thing for me is a kind of forward planning/goal-oriented thinking idea: what do I need to do, what do I need to do so I can do that, what do I need to do so I can do that, and so on.

With the regular tower, this manifests itself as the idea of recursion: as part of moving all the discs, I naturally have to move the biggest disc at some point, and to be able to do that I need a clear spot to move it to (because it’s too big to sit on top of anything else), so I have to stack all the other discs up somewhere.  So in order to solve an n-disc tower, I must solve the (n-1)-disc tower, move the biggest disc, then solve the n-1 disc tower again.

If this is going over your head a bit, I’m going to link you to a nice video that Grimlock Master linked me to yesterday that explains this from the ground up: https://www.youtube.com/watch?v=2SUvWfNJSsM .

So, moving on to our actual puzzle.  The idea is still the same, though: at some point, we’re going to have to move that biggest disc, the bottom blue one, and to do that, we’re going to need to get the other three discs to the currently empty peg.  And to do that, we need to get the bigger red disc onto the empty peg.  So our opening moves are:

(so we’re two moves in so far, for those keeping count for that eleven-move limit).  All right, next we need to get the two smaller discs on to the bigger red disc, and that’s simple enough - it’s just a two-disc tower:

Five moves so far.  Now we can move that biggest disc:

Six moves.  And now it’s time to do the whole thing mirror-imaged in reverse to finish the job off:

Nine moves - happily that smaller blue disc is now exactly where we need it.  And then it’s just a case of moving the bigger red disc to its new home, and putting the smaller red disc on top of it:

And we’re finished in eleven moves!  Nicely done.

So here’s a neat extra thing about the towers of Brahma/Hanoi: you can map all possible legal states and moves out onto a version of the Sierpinski Gasket or Sierpinski Triangle. For those not familiar with this famous fractal: imagine the Triforce from Zelda.  Now imagine each of those triangles is, itself, a Triforce.  Now imagine each of the triangles that make these mini-Triforces up is also a Triforce.  Now keep doing that forever.  In short, this badboy.

But as I was saying, you can use this fractal to map out all these different positions the pieces can be in - and I’ve done just that!  First, here’s the case with four discs.

I should explain the labelling here.  I’ve called the three poles A, B and C, and coloured them red, green and blue.  The sequence of four letters at each node in the network is the current peg of discs 1 through 4, 1 being the smallest, 4 being the largest.  The three starting positions for the conventional puzzle are on the three corners of the triangle - I’ve drawn boxes around them in cyan.  And if you follow the side edges of the triangle (one such edge highlighted in cyan), you’ll find the fastest routes to solve the conventional puzzle by getting the whole stack to a different pole.  And you can see that for four discs, it’s fifteen moves.  This is the shortest possible route, because it’s a straight line.

Now.  The six possible start points for the “swapping” puzzle have magenta boxes drawn around them, and to get from one to another you have to follow, for instance, the route highlighted in magenta.  Which, as you can see, is eleven moves long.  It’s less obvious that this is the shortest route, but there aren’t many other ways around that big triangular hole in the middle - and if you count it out, you’ll see that going the other way takes fifteen moves.

What about the extension puzzle I suggested, with two sets of three discs that needed swapping?  Well, okay, here’s the six disc version.  You might want to download this one so you can get a proper look, it’s huge.  This time, we have a sequence of six letters to show which peg we’re on.

Solving a regular tower of six, by the way, takes 63 moves (in fact, for n discs, solving the regular tower will take (2^n - 1) moves - the proof is left as an exercise to the reader).  And you can see that the path this time for our “swap” puzzle takes 45 moves.  I’d draw it all out, but it’d take quite a while and this blog post’s already really long.

Still, it’s remarkable what you can connect together across different fields.

[paulspuzzles]

Puzzle #10

A bit more Techniquest and Mathamagic cribbing here, although it in turn is based off a much older puzzle.

So you’re probably familar with the Tower of Brahma/Tower of Hanoi puzzle.  You have three pegs, and a set of discs increasing in size on one of the pegs.  In this illustration here, we have four discs:

The goal of this puzzle is to get the stack of four discs from one peg to either of the others, obeying the following rules:

You may only move one disc at a time.

The disc has to go to one of the other two pegs

Bigger discs cannot be placed on top of smaller ones.

And it’s an excellent puzzle, requiring a good deal of strategic thinking and forward planning.  But it’s also a little old hat - the method for finding the solution with the fewest moves (15 for four discs, incidentally) is very well known at this point, and even if you don’t know it, it’s such a famous puzzle that it’d be easy enough to look up.

So my actual puzzle today is going somewhere slightly different:

We’ve split the discs up onto two pegs, so the red (odd) are on one peg and the blue (even) discs are on the other.  Now your goal is swap over the two stacks of discs, following the same three rules as for the regular puzzle.  The least number of moves this puzzle can be solved in is 11 - can you find that solution?

And if you’re feeling daring, let’s say you had six discs split into two stacks of three.  The minimum number of moves to swap the stacks over now is 45 - can you find that solution?

[paulspuzzles]

Not-Puzzle #1

Figured I’d change it up with something mathsy that isn’t actually a puzzle.  I’ll probably be doing more of these as we go.  Sometimes (often!) I find something interesting but I can’t find a way to phrase it as a puzzle.

Today I’m going to talk about cricket stats, and a pair of spreadsheets I’ve been curating over the past few years.  With the next Ashes series due to start in only a couple of days, this seemed like as good an opportunity to publish them as any.

The first of these is about stats collected on the number of runs per innings scored by England batsmen of the modern era (my definition of “modern” being “still playing when I first got interested in cricket”, so anyone who was still playing in 2000.  Mike Atherton is the first batsman in this workbook, for instance).  Anyone with at least 50 innings and one century who’s played since then should be in there (so Stuart Broad’s in there!)

The data is divided up as “how many scores did they make in each ten-run interval”, so from 0-9, 10-19 and so on, with not-outs added on the end in a different colour.  For the average batsman, this follows an exponential distribution: https://en.wikipedia.org/wiki/Exponential_distribution .  I first learnt that batsmen’s runs followed this distribution years ago in an article by maths and cricket populariser Rob Eastaway, although I can’t for the life of me find it now.

There’s a general logic to it - if a batsman has a certain chance to get out any ball, then they are more likely to get out on their first ball than on “specifically” their 107th ball, or whatever.  And similarly for runs - for most batsmen in the history of the game (even Bradman!), a duck is their most common score.

Also included for each batsman is a small pie chart showing their percentages of single-figure scores, “starts” (scores from 10-49), fifties (50-99) and hundreds (100+).  The latest version, correct to England’s most recent Test match, can be found here: https://www.dropbox.com/s/hqqquuqkew1g16u/england%20batsmen%202017.ods?dl=0

It’s fun to see how different batsmen deviate from the norm: Ian Bell above, for instance, had way more single-figure scores than would be typical, but once he reached double figures he was quite consistent at reaching 50 - though again, not necessarily the best at turning fifties into hundreds.

Michael Vaughan below had the exact opposite strengths and weaknesses - very good at getting starts, awful at turning starts into fifties, excellent at turning what fifties he got into hundreds:

You can even group batsmen like this: Joe Root is very much in the Ian Bell half of these breakdowns in terms of getting to fifty tremendously often but not necessarily converting.  Andrew Strauss and Kevin Pietersen were both very much in the Vaughan camp of good at getting starts, less good at turning them into fifties, but good at turning fifties into hundreds.

Of course, if anyone feels like using this for anything, or perhaps going further back into history or graphing batsmen (or women) from another country, feel free!  As long as you credit me for it and let me know about it, that’s fine.

Now then, the other spreadsheet is less numerical in nature but is still basically a graph.  Or a chart, maybe.  This one covers the entire span of England’s history of Test Cricket, and is basically a giant cross-reference of which England players played in which teams.

So for instance, here’s the evolution of the side from the 2004 series again New Zealand and the West Indies to the 2010/11 tour of Australia.  As is traditional for scorecards, captain is denoted by *, wicketkeeper by †.  It notes the year, the opponent and whether each match was won or lost.

It’s fun to spot patterns - the way that successful periods are often marked by smooth continuity of selection and the side rarely changing, and the giant cliffs in less successful periods as selectors scramble to try and subsequently discard players.

I even learnt about all sorts of oddities compiling this, like the 1912 Tri-Series between England, Australia and South Africa, or the 1929/30 simultaneous tours to West Indies and New Zealand.  There’s an entertaining riot of back-and-forth colour for those series.

You can find this spreadsheet here: https://www.dropbox.com/s/14sa4qi1f4dyzfp/england%20cricket%20caps.ods?dl=0

Again, if you want to use this for something or maybe adapt it for your own cricket team, feel free, as long as you let me know and give me credit.  Hope these prove to be fun things to look through!

[paulspuzzles]

Solution #9

Click “Keep reading” to see the solution!

So we need to know the perpendicular height of this triangle to find out its area (yes, yes, we could use ½*a*b*sin(C) = ½a²sin(60°).  I’ll be using that at the end, funnily enough.  But humour me a minute).  Well, let’s drop a perpendicular and see what we get:

We’ve now split this equilateral triangle into two right-angled triangles.  These right-angled triangles have a hypotenuse of a, and one of their short sides is a/2 (half the length of a side of the triangle).  With a bit of Pythagorean magic, we get:

x² + (a/2)² = a² x² = a² - a²/4 x² = 3a²/4 x² = (a√3)/2

So the perpendicular height of an equilateral triangle side length a is a√3/2.  This is a very important relationship in trigonometry, as it lets us get exact values for sin(30°) = cos(60°) = ½, sin(60°) = cos(30°) = √3/2, tan(30°) = 1/√3, and tan(60°) = √3.

Anyway, area of a triangle is ½*base*perpendicular height, so:

Area = ½*a*a√3/2 = a²√3/4.

Nice.  And yes, this checks out with the ½a²sin(60°) formula from earlier, since sin(60°)  = √3/2.

Moving on... well, a regular hexagon is, after all, just six equilateral triangles grouped together:

So its area is simply 6*a²√3/4 = 3a²√3/2.

The octagon goes in a slightly different direction.  We can split it up into nine parts, as follows:

By Pythagoras again, we can see that the lengths of the short sides of the isosceles right-angled triangles (let’s just call them iRATs) in the corners is a/√2.  This gives us:

1 square, area a²

4 iRATs, each with area ½(a/√2)² = a²/4

4 rectangles, each with area a*a/√2 = a²/√2, or a²√2/2 because it’s easier to multiply top and bottom through by √2 and get your surd on the top.

Let’s put that all together:

a² + 4a²/4 + 4a²√2/2 = a² + a² + 2a²√2 = 2a² + 2a²√2 = 2a²(1 + √2)

There we go.  You might even have noticed a shortcut here: those four iRATs can be combined together geometrically to make another square side length a, area a².  We showed this this algebraically here, but one of the great things about maths is how many ways there are to skin a cat.

Now then, on to that dodecagon.  As I said at the beginning, I’ll be using the area = ½*a*b*sin(C) formula here.  We can split this thing up into twelve triangles meeting at a centre point.  Since there are 360° in a full circle, dividing that by twelve gives us an angle of 30° for the pointy bit of this triangle:

So the area for one of these triangles is ½*r²*sin(30°), and we showed earlier that sin(30°) is ½.  So the area of a triangle is ¼r².  And since we have twelve triangles, the total area of this dodecagon is 3r².

That’s a rather pleasing result, I think. If nothing else, it sets a nice lower bound for π of 3 (granted, you can do a lot better than that).

I probably should have expected this of course, but Wikipedia has a lovely table of regular areas for polygons in terms of different properties of them here: https://en.wikipedia.org/wiki/Regular_polygon#Circumradius .  But it’s still fun to work this stuff out for yourself.