#regular polygons
Explore tagged Tumblr posts
Text
shout out to regular star polygons . very underrated
my favorites out of the smaller ones are {9/3} and {10/3}
#one of my fav infinite families in mathematics#especially the ones that aren't {n/2}. those ones are very cool#also noneuclidian regular polygons are awesome#mathematics#regular polygons#jup talks#regular star polygons#geometry
4 notes
·
View notes
Text
Since everyone likes regular shapes so much:
#shapes#2d shapes#regular polygons#polygons#maths poll#tbh if you like hexagon you probably like equilateral triangle too - they're buddies
20 notes
·
View notes
Text
Weird fact of the day. I can’t say this geometric theorem is in the least bit intuitive.

Mathematical fun fact of the day 2.
The maximum number of diagonals of the regular n-gon that meet at a point other than the center is 7. This can only be achieved when n is a multiple of 30.
For more details see the paper: The number of intersection points made by the diagonals of a regular polygon by Bjorn Poonen and Michael Rubinstein
204 notes
·
View notes
Note
what app did you cut the background?

i use photopea, i cut my renders out manually using the lasso tool and eraser tool for smaller details!
#★ asks!#i use specifically the polygonal lasso. however depending on your preference the regular lasso tool or the pen tool work well too#there Is the wand tool but it doesnt work very well since it tend to leave really jagged lines nor does it really select things very well
12 notes
·
View notes
Text
this is me off one hit of hyperbolic geometry
#wdym you can have regular polygons with all right angles.....#WDYM YOU CAN HAVE REGULAR POLYGONS WITH NO ANGLES....#like i Get It but also Why#boycritter et al
7 notes
·
View notes
Text
cybertrucks are certainly a car of all time. everytime i see one it somehow pulls me out of my suspension of disbelief despite it being real life and having no disbelief to suspend. what an ugly vehicle
#i refuse to believe these are real cars.#my neighbor has one and ive seen quite a few in town#they're soooo ugly#they make regular teslas look cute in comparison (a car i also think is ugly but. less so compared to the polygonal horrors)
8 notes
·
View notes
Text
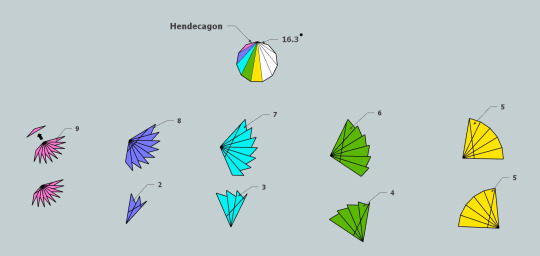
Polygon Angles
Ghee Beom Kim teaching over on FB. "When you triangulate regular polygons (n-gons), you get special triangles with a distinct property: the two larger angles are always exact multiples of the smallest angle. The key condition for these triangles is that their smallest angle must measure 180/n degrees, where n is a natural number. The image provided illustrates this concept."
And Dominic Pons @xponentialdesign had this...

4 notes
·
View notes
Text
really bad chess is kicking my ASS
#it's this game on a site called puzzmo that's run by polygon#basically you and your opponent get randomized chess pieces#im not even good at REGULAR chess#yesterday and today the player side got three queens and im still getting destroyed#PARTIALLY BC TODAY THE OPPONENT HAS FOUR CASTLES IN A ROW. HEP HEP HEP#i took out three with a bunch of Epic Bishop Sacrifices but have gotten myself in a REALLY shit position#this is my second attempt i dont wanna go back to quad castle hell pleaaaaaasee ahuuhh ahoouhh sob#witness me
8 notes
·
View notes
Text
One edge is on the x axis and offset from the origin on the y axis by the apothem. The side length allows us to know the exact coordinates of its vertices. We know the interior angle of the vertex figure as well.
We can rotate around the x axis with a vertex as the center in order to find the edge's second face, but how do we find the axis of the next edge to rotate around? Perhaps we can use the interior angle of the face to find the second edge of the vertex and rotate that vector as we do the face in order to follow its movement and define the next axis.
Carry through the loop a "previous axis" (axis a) socket along with the "current axis" (axis b). Initialize axis a as (1,0,0) rotated about the z axis by the interior angle to align with the adjacent edge and initialize axis b as simply (1,0,0). Rotate the face about axis b and let b plug into a. Rotate a about axis b and let the result plug into b. Repeat n-1 times where n is the number of vertices in the vertex figure.
Sure yeah I'll solve my geometry nodes issues lying in bed half awake instead of while actually having the thing in front of me.
#sfw#personal#ok to reblog#<- dunno why you would but it's perfectly allowed#not even discouraged at all#and yes I am back on my old regular polyhedron project although most of my work today was refamiliarizing myself with my old nodes#and like “uhh wait a minute it's been over a year why does this output 'convex apothem' and 'true apothem'??”#(the answer is sometimes a polygon is not convex but it might be useful to know how it would behave if it were)#(I made one node group that just takes a Schläfli symbol and spits out every measurement I could think to calculate. lazily evaluated ofc)#(I love you geometry nodes I love you lazily evaluated fields I love you repeat zones I love you new features I love you old features )
4 notes
·
View notes
Text
Actually that seems to be part of an Obama Rhmbicosidodecahedron

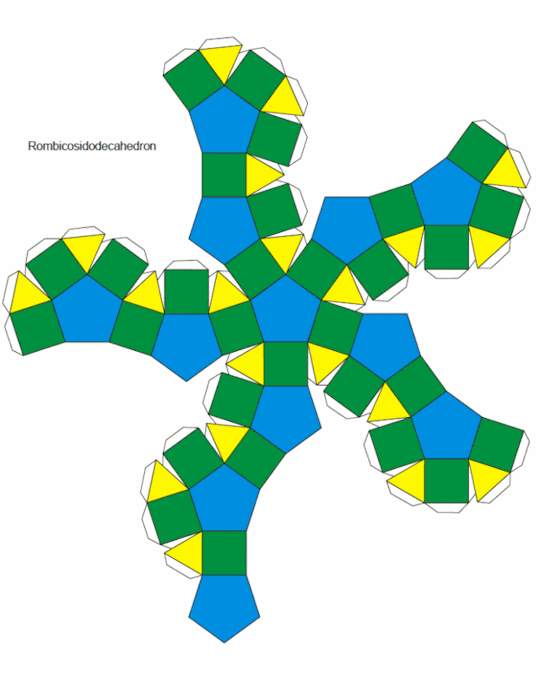


#rhombicosidodecahedron#which is an Archimedean Solid! Every vertex is the same but not every face.#in fact all of the faces are made of regular polygons#fun fact: soccer ball (truncated icosahedron) is also an Archimedean solid#math
55K notes
·
View notes
Text
Johnson Solids & Unsightly Definitions
Something I am fascinated by, beguiled by, is the Johnson Solid, a special class of 3D polyhedron. If I give you the definition of a Johnson Solid, I will have to mention a number of caveats, and I don’t think that’s a nice way to start this article, so let’s do what mathematicians do best and start with something simpler. Quadrilaterals: 4 walls and a rule A quadrilateral is a shape in two…

View On WordPress
#Archimedean solids#geometry#math#mathematics#Maths#periodic table#platonic solids#polyhedron#polytope#regular polygon
0 notes
Text
Ancient Greek Women Mathematicians you didn't know about

Αίθρα - Aethra (10th - 9th century BC), daughter of the king of Troizina Pitthea and mother of Theseus, knew mathematics in another capacity unknown to many. So sacred to the beginnings of the most cerebral science, Aethra taught arithmetic to the children of Troizina, with that complex awe-inspiring method, since there was no zero… and the numbers were symbolically complex, as their symbols required many repetitions.
Πολυγνώτη - Polygnoti (7th - 6th century BC) The historian Lovon Argeios mentions Polygnotis as a companion and student of Thalis. A scholar of many geometric theorems, it is said in Vitruvius' testimony, that she contributed to the simplification of arithmetic symbols by introducing the principle of acrophony. She managed this by introducing alphabetic letters that corresponded to each in the initial letter of the name of the number. Thus, Δ, the initial of Δέκα (ΤΕΝ), represents the number 10. X, the initial of Χίλια (Thousand), represents the number 1000 etc. According to Vitruvius, Polygnoti formulated and first proved the proposition "Εν κύκλω η εν τω ημικυκλίω γωνία ορθή εστίν" - "In the circle the angle in the hemi-circle is right angle."
Θεμιστόκλεια - Themistoklia (6th century BC). Diogenes the Laertius scholar-writer mentions it as Αριστόκλεια - Aristoclia or Θεόκλεια - Theoclia. Pythagoras took most of his moral principles from the Delphic priestess Themistoclia, who at the same time introduced him to the principles of arithmetic and geometry. According to the philosopher Aristoxenos (4th century BC), Themistoclia taught mathematics to those of the visitors of Delphi who had the relevant appeal. Legend has it that Themistoclia decorated the altar of Apollo with geometric shapes. According to Aristoxenos, Pythagoras admired the knowledge and wisdom of Themistoclia, a fact that prompted him to accept women later in his School.
Μελίσσα - Melissa (6th century BC). Pupil of Pythagoras. She was involved in the construction of regular polygons. Lovon Argeios writes about an unknown work of hers: "Ο Κύκλος Φυσίν - η Μελίσσα - Των Εγγραφομένων Πολυγώνων Απάντων Εστί". (The title translates to "The circle is always the basis of the written polygons" or so.)
Τυμίχα - Tymicha (6th century BC). Thymiha, wife of Crotonian Millios, was (according to Diogenes Laertius) a Spartan, born in Croton. From a very early age, she became a member of the Pythagorean community. Iamblichus mentions a book about "friend numbers". After the destruction of the school by the Democrats of Croton, Tymicha took refuge in Syracuse. The tyrant of Syracuse, Dionysios, demanded that Tymicha reveal to him the secrets of the Pythagorean teaching for a great reward. She flatly refused and even cut her own tongue with her teeth and spat in Dionysius' face. This fact is reported by Hippobotus and Neanthis.
Βιτάλη - Vitali or Vistala (6th – 5th century BC). Vitali was the daughter of Damos and granddaughter of Pythagoras, and an expert in Pythagorean mathematics. Before Pythagoras died, he entrusted her with the "memoirs", that is, the philosophical texts of her father.
Πανδροσίων ή Πάνδροσος - Pandrosion or Pandrossos (4th century AD). Alexandrian geometer, probably a student of Pappos, who dedicates to her the third book of the "Synagogue". Pandrosion divides geometric problems into three categories:" Three genera are of the problems in Geometry and these, levels are called, and the other linear ones."
Πυθαΐς - Pythais (2nd century BC). Geometer, daughter of the mathematician Zenodoros.
Αξιόθεα - Axiothea (4th century BC). She is also a student, like Lasthenia, of Plato's academy. She came to Athens from the Peloponnesian city of Fliounda. She showed a special interest in mathematics and natural philosophy, and later taught these sciences in Corinth and Athens.
Περικτιόνη - Periktioni (5th century BC). Pythagorean philosopher, writer, and mathematician. Various sources identify her with Perictioni, Plato's mother and Critius' daughter. Plato owes his first acquaintance with mathematics and philosophy to Perictioni.
Διοτίμα - Diotima from Mantineia (6th-5th century BC). In Plato's "Symposium", Socrates refers to the Teacher of Diotima, a priestess in Mantineia, who was a Pythagorean and a connoisseur of Pythagorean numerology. According to Xenophon, Diotima had no difficulty in understanding the most complex geometric theorems.

Iamblichos, in his work "On Pythagorean Life", saved the names of Pythagorean women who were connoisseurs of Pythagorean philosophy and Pythagorean mathematics. We have already mentioned some of them. The rest:
Ρυνδακώ - Rynthako
Οκκελώ - Okkelo
Χειλωνίς - Chilonis
Κρατησίκλεια - Kratisiklia
Λασθένια - Lasthenia
Αβροτέλεια - Avrotelia
Εχεκράτεια - Ehekratia
Θεανώ - Theano
Τυρσηνίς - Tyrsinis
Πεισιρρόδη - Pisirrodi
Θεαδούσα - Theathousa
Βοιώ - Voio
Βαβέλυκα - Vavelyka
Κλεαίχμα - Cleaihma
Νισθαιαδούσα - Nistheathousa
Νικαρέτη - Nikareti from Corinth
There are so many women whose contribution to science remains hidden. We should strive to find out about more of them! For more information, check out the books of the Greek philologist, lecturer, and professor of ancient Greek history and language, Anna Tziropoulou-Eustathiou.
#I noted those names down from different sources and I copied a few more info from a comment under a video#international women's day#science#history#mathematics#pythagoras#greek women#greek history#hellas#women in stem#women in science#women in mathematics#Pythagorean mathematics#women's history
792 notes
·
View notes
Text




AquaTV
(TV CONVERTED TO FISH TANK)
Are you tired of paying for hundreds of channels and a dozen of subscriptions that you never use? Do you often need to recharge in nature, but you can't be bothered to get up? AquaTV is the AquaSolution to all these problems, and more! Comes with the most immersive documentary known to simkind. Don't forget to feed it!
Swatches: 14 (regular, pastel, neon), 6 (corporate)
Polygon count: 443
Custom thumbnails
Appears in game as: AquaTV
Credits // Software: S4Studio, GIMP, Blender / Sites: Canva / Mesh: mostly EA (some parts were modified by me) / Textures: EA (partly modified, also recolored)
Terms of Use // Free to modify mesh/textures/whatever under the conditions that you're not a bigot, you don't paywall it and you give credit. Don't forget to rename the file to remove my name from the item.
MEDIAFIRE - SIMFILESHARE (regular palette)
MEDIAFIRE - SIMFILESHARE (pastel palette)
MEDIAFIRE - SIMFILESHARE (neon palette)
MEDIAFIRE - SIMFILESHARE (corporate palette)
#sims 4 cc#sims 4 decor#sims 4 custom content#ts4#s4cc#maxis match#s4 custom content#sims 4#ts4cc#simblr#sims cc#s4mm
470 notes
·
View notes
Text
Inspired by this post by @thanergetic-hyperlinks, I present to you
Tessellations of the Nine Houses
(Or "I can't really draw figurative art so my Locked Tomb fanarts are geometrical vector drawings")
"A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps." — Wikipedia.
Making tilings themed after each necromantic House seems obvious: for each House you pick a tile with the same number of sides as the number of the House; but this does present some challenges for some of the Houses.
note 1: this might give the impression that I first decided on the symbols and then found patterns to match them in a very organized and motivated manner; in practice it was much more chaotic and multidirectional, the patterns informing the symbols as much as the symbols informed the patterns; this is fine since symbolism is entirely associative and arbitrary anyway
note 2: I added alt-texts for all the images, but I have no idea of how to properly describe abstract geometric art; if you feel you can do a better job than I did, feel free to put your fingers where your mouth is--wait, hang on-- I mean feel free to provide better descriptions if you can
note 3: looking forward to the geometry nerds explaining to me how I got basic geometric details wrong, friggin nerds
The First House
The First House seems obvious, as a shape with one side is an ellipse (of which the circle is a special case). There's just one problem: ellipses do not tile the plane. No matter how much you stretch them and deform them, the very nature of ellipses means you'll always have gaps or overlaps.
So we cheat and we work with overlaps: turns out there is a history of tilings that use circles as a construction pattern, then turn the overlapping sections into the actual tiles. Such patterns have been used extensively in European and Middle Eastern art, and have also been associated with the New Age movement, so it fits Jod's style perfectly. And so we get this:

The different cells correspond to different House colors, with the resulting gothic stained-glass appearance quite in line with the Roman Catholic Empire vibe Jod is going for. The overlapping circles convey the intricacy of the relation between the First House and the eight other, both autonomous from it yet intrinsically part of it.
The Second House
There's a variety of geometrical shapes that have two sides, but most of them don't tile the plane, altho there is one that does — if we take a crescent shape and slightly thicken it so that the inner and outer curves are identical, we can do this:

The waving pattern is of course evocative of the flag of conquest which the Cohorts of the Second House have planted on many worlds.
The Third House
With the Third House things get a lot easier, because equilateral triangles are one of the three regular polygons (where all sides are the same length and all angles are identical) that tile the plane all by themselves without needing any other shape! Which however doesn't mean we have to be boring; we can have a little bit of fun:

Flowers for the beauty and ionizing radiation warning signs for the rancid vibes.
The Fourth House
Squares are the second regular polygons that tile the plane by themselves, so again our job is easy here, altho we still want to not go for the easiest option in order to be able to work in some symbolism:

The four big navy squares with a small white square at the center of course evoke the number five and the shadow of the Fifth House's regency over the Fourth.
The Fifth House
Regular pentagons do not tile the plane, so we have to use a more unusual shape — there are many options, but obviously we want to again pick one that offers some interesting numerical symbolism:

The cross-like patterns of course bring up the number four and the hold of the Fifth House over the Fourth. As for the crosses themselves and the fact that they appear to be made of wooden stakes, well uh… Abigail Pent, Vampire Hunter??? She does have Van Helsing vibes.
The Sixth House
Hexagons are the third and last regular polygons that tile the plane on their own. But this is the Sixth House we're talking about, things need to look orderly but in a convoluted way. So how about multiple levels of recursion:

The apparent complexity of the pattern is created by different orientations of a small number of elements, either 3 irregular hexagons, or 1 patterned regular hexagonal tile, depending on how you look at it, in line with the kind of hermetic scientism one imagines the Sixth House indulges in. The result is those apparent three-dimensional elements and emerging higher-order patterns, including that of ꙮ, the Multiocular O found in exactly one word of one 15th century Old Church Slavonic translation of the Book of Psalms ("серафими многоꙮчитїй" many-eyed seraphim).
The Seventh House
Regular heptagons do not tile the plane, but they don't need much tweaking to work, which is fine since for the Seventh House we want something deceptive yet simple (deceptively simple? deceptive in its simplicity?):

Hearts for the beauty, snake scales for the poison [the Seventh House is on Venus, the planet named after the Roman Goddess of love, but etymologically "Venus" is actually the same root as "venom", and of course "Septimus" resembles "septic" — tho in that case there's no etymological connection, it's just a happy coincidence].
The Eighth House
Octagons do not tile the plane, but they come pretty close, so we can give the Eighth House a simple, stern, but slightly threatening pattern:

Boring sterile bleached temple mosaic, with just a little bit of passive-agression, a perfect fit for Evangelical Christians Tumblr puritans the Eighth House.
The Ninth House
And so we reach the Ninth House. Now the thing about the Ninth House is that, even by imperial standards, they're huge freaks, like they're completely unhinged heretical weirdoes. So, when it comes to their tiling, we need to get weird, like, a lot weirder than we've been so far, and this will require some context, so get ready because now we're officially going on a wild tangent.
So far all the tilings we've seen were periodic. That is, they were drawing a pattern that repeats itself indefinitely in all directions.
But starting in the 1960s, mathematicians began to study aperiodic tilings, tilings that don't repeat; you can keep expanding them forever and never exactly find back the original pattern you started with. The first mathematical proof of such a pattern was made in 1964 and theoretically required 20,426 distinct tile prototypes… This was soon refined to just 104 tile prototypes, then a mere 40. By 1971, it was mathematically demonstrated that you could make such a pattern with just 6 tile prototypes.
Except that was a lie.
Note that I said mathematically demonstrated. As it turns out there was an aperiodic pattern with just 5 tile prototypes, known as Girih, that had been used in Islamic art… since at least the 13th century — but it had historically been treated merely as an element of architectural design, and its mathematical properties weren't studied until 2007.
Then in 1973 this guy Penrose came along and demonstrated you could make an aperiodic tiling with just 2 tile prototypes. So now the goal was to find the ultimate aperiodic tiling, the one that would use only one tile prototype. Given how fast the field had progressed so far, it seemed that this discovery was imminent.
It took 50 years.
Not only that, but it was the work of amateur mathematician David Smith who accidentally discovered a 13-sided polygon that could make an aperiodic tiling all by itself (he then had his discovery checked by and co-authored a paper with a number of professional mathematicians).
EXCEPT THAT WAS A LIE AGAIN.
In turns out an aperiodic tiling using only one tile prototype had already been found… in 1936. But since the study of aperiodic tilings only started in the 60s, its significance in that domain wasn't understood at the time. It was seen as significant, but for an entirely unrelated reason: it was the first demonstration of a polygonal shape that needed only two copies of itself to completely enclose the original one — many mathematicians before that point thought the minimum possible was 3 (think of the Triforce from Zelda, with one equilateral triangle completely enclosed between three other identical triangles).
And coincidently, that shape happens to be a highly-irregular nonagon [yes "enneagon" is """technically""" more correct but "nonagon" has been used since the 17th century and is more common and it has Nona in it and Nona loves you]. So here it is, the Voderberg tiling, the freakish freakish tessellation of the Ninth House:

Like you see this and you're like "what is this, what is that thing, that's not a tiling, what the fuck is that" — but it is, it is a tiling, you can keep adding the freaky polygon and it keeps expanding outward forever, with no gap, no overlap, and with an ever-changing pattern. A double-spiral radiating outward, for Anastasia and Samael, Anastasia and Alecto, Alecto and Harrowhark, Harrowhark and Gideon.
And if you were thinking that this last one must have been significantly harder to draw than the other ones, you would be correct.
447 notes
·
View notes
Text



Top: Shiverians from Super Mario Odyssey as they appear during regular gameplay.
Middle: due to the large amount of Shiverians in the audience during the Bound Bowl minigames, they are replaced with a low-polygon version during this. While this can not be seen in-game, zooming in on the low-quality Shiverians shows that their eyes are angled as through they are sad.
Bottom: this is surprisingly not the only time low-quality versions of characters appear sadder than the regular ones in Mario games. In Paper Mario: The Thousand-Year Door, the low-quality female Toads in the Glitz Pit audience do not smile like the high-quality ones.
Main Blog | Twitter | Patreon | Small Findings | Source
1K notes
·
View notes
Text
being a solids/tilings fan as a pup and then being exposed to hyperbolic geometry is so wild. like u can prove the finitude of euclidian vertex transitive tilings but in hyperbolic geometry there are simply infinitely many, cus you're just allowed to bend the space to fit arbitrarily many arbitrarily large regular polygons around a corner
857 notes
·
View notes