#Big O Notation and Time Complexity Analysis | Explore Tumblr posts and blogs

emmajacob03 · 7 months ago

Text

How Assignment Help Can Aid in Mastering Data Structures and Algorithms

Mastering data structures and algorithms is a crucial step for anyone venturing into the world of computer science. These concepts form the backbone of efficient software development and problem-solving.

This is where urgent programming assignment help services comes into play. The services from AssignmentDude provide expert guidance and support, helping students navigate through the intricacies of data structures and algorithms.

From personalized learning to urgent assignment help, these services cater to a wide range of needs. They can be a lifeline for students facing tight deadlines or struggling with complex coursework.

In this article, we delve into how assignment help can aid in mastering data structures and algorithms. We’ll explore the benefits, how it works, and the potential impact on a student’s learning curve and academic performance.

So, whether you’re a computer science student or a professional looking to upskill, read on to discover how assignment help can enhance your understanding of these fundamental concepts.

Understanding the Complexity of Data Structures and Algorithms

The realm of data structures and algorithms is vast and intricate. It forms the core of computer science principles that drive efficient programming. Grasping these concepts requires strong logical reasoning and problem-solving skills.

Data structures such as arrays, linked lists, stacks, and queues lay the groundwork for managing data effectively. Each has unique attributes and uses, making it essential to discern their differences. Comprehending these nuances allows one to select the best-suited structure for various problems.

Algorithms, on the other hand, are systematic approaches to solving tasks. They encompass methods like recursion, dynamic programming, and sorting techniques. Mastering algorithms involves learning how to design and optimize processes for specific needs.

The challenge also lies in understanding algorithm efficiency and optimization. Complexity analysis, including Big O notation, plays a critical role in evaluating performance. This involves assessing time and space efficiency, which can be daunting for many learners.

In summary, the complexity arises from the need to integrate theoretical knowledge with practical application. Students often must navigate a plethora of academic content, honing skills that are pivotal in developing clean, efficient, and effective code.

The Role of Assignment Help in Learning Data Structures and Algorithms

Assignment help services play a crucial role in demystifying data structures and algorithms for learners. These services provide expert guidance tailored to individual learning styles and challenges. By addressing specific needs, they enhance comprehension and retention of complex topics.

One key advantage is personalized attention from experienced tutors. These professionals help break down intricate concepts into digestible pieces, making the learning process smoother. This personalized approach allows students to focus on areas of difficulty, ensuring a deeper understanding.

Furthermore, assignment help services offer access to a diverse range of resources. From practice problems to interactive tools, these resources cater to varied learning preferences. This rich array of materials supports students in mastering both theoretical and practical aspects.

Here’s how assignment help can assist learners:

Clarifies complex concepts through expert explanations

Provides access to a wealth of learning materials

Offers support tailored to individual learning needs

The role of assignment help extends beyond immediate academic tasks. It prepares students for long-term success by building a solid foundation in data structures and algorithms. Through this support, learners can develop the confidence and skills required to tackle advanced topics in their studies and future careers.

Benefits of Seeking Assignment Help for Data Structures and Algorithms

Assignment help offers numerous benefits for those delving into data structures and algorithms. It caters to the unique needs of each learner, promoting a more effective learning experience. By providing tailored assistance, it helps unravel the complexities of these subjects.

One significant benefit is improved time management. With guidance from assignment experts, students can allocate their efforts more effectively. This allows them to focus on essential concepts without feeling overwhelmed by tight deadlines.

Access to expert insights is another advantage. Tutors often bring a wealth of practical experience and deeper understanding that textbooks may not offer. Their insights can illuminate the intricacies of algorithms and data structures, enhancing the educational journey.

Here are some key benefits of assignment help:

Enhanced time management skills

Insights beyond standard curricula

Reduction of academic stress and anxiety

Moreover, assignment help services can boost academic performance significantly. By clarifying doubts and reinforcing weak areas, they prepare students better for exams and assessments. This performance boost often translates into higher grades and academic success.

Beyond academics, these services can nurture critical thinking and problem-solving abilities. By working through tailored exercises, learners develop the skills necessary to tackle real-world challenges. This preparation is invaluable for students aspiring to enter technical fields.

Ultimately, assignment help serves as a bridge between theoretical knowledge and practical application. It equips students with the confidence and expertise required to excel in data structures and algorithms, fostering long-term academic and professional success.

Personalized Learning: Tailoring Help to Your Needs

Personalized learning is a key advantage of assignment help services. It acknowledges that every student learns differently. By adapting to individual learning styles, these services offer the flexibility needed to grasp complex topics.

Customized assistance enables learners to progress at their own pace. Some students may require additional support with particular subjects, such as recursion or graph theory. Others might seek deeper insights into algorithm efficiency. Personalized learning addresses these varied needs.

Tailored help is not just about correcting errors. It focuses on boosting a student’s strengths while addressing weaknesses. The goal is to provide a comprehensive understanding that encourages growth and confidence in the subject matter.

Personalization is not limited to the academic curriculum. Tutors also consider a student’s personal preferences and prior knowledge. This well-rounded approach ensures that each student receives the specific guidance needed to excel in data structures and algorithms.

Overcoming Challenges with Expert Guidance

Understanding data structures and algorithms can be daunting. Students often face challenges due to their complexity and abstract nature. Expert guidance can make a significant difference in overcoming these hurdles.

Assignment help services offer access to experienced tutors who specialize in these topics. These experts are well-versed in both theory and practical applications, making them ideal mentors for students. Their insights extend beyond textbooks, providing a richer learning experience.

Here are some ways expert guidance can help:

Clarifying complex concepts like recursion and dynamic programming.

Offering strategies for effective problem-solving.

Providing real-world examples to enhance understanding.

Assisting with debugging and code optimization.

Breaking down algorithms into simpler components for easier comprehension.

Tutors can pinpoint specific areas where students struggle. They then develop strategies to address these issues. This targeted approach can accelerate learning and make mastering the subject more accessible.

Working with experts also encourages critical thinking. Students learn to approach problems methodically, analyzing potential solutions thoroughly. This cultivates a problem-solving mindset that is essential for success in computer science.

Urgent Assignment Help: Meeting Tight Deadlines

Academic life often comes with tight deadlines. Students can feel overwhelmed balancing coursework with other responsibilities. Urgent assignment help offers a solution, ensuring they meet due dates without compromising quality.

These services are equipped to handle last-minute requests. They provide rapid assistance, often delivering results in hours rather than days. This is especially beneficial for students juggling multiple commitments.

Urgent assignment help doesn’t just involve speed. It maintains the quality of work, even under pressure. Expert tutors are skilled at producing well-researched and accurate solutions quickly.

Time zone differences are also a non-issue with these services. They typically operate 24/7, ready to assist students at any time. This round-the-clock availability means help is just a click away, regardless of location or time of day.

Such assistance allows students to focus on understanding key concepts, rather than stressing over looming deadlines. It ensures both timely submissions and effective learning.

“Do My Programming Homework”: Practical Implementation Assistance

When it comes to learning data structures and algorithms, practical application is key. Theoretical knowledge needs to be complemented with hands-on experience. This is where “Do My Programming Homework” services come into play.

These services specialize in providing practical implementation support. They help students apply data structures and algorithms in programming assignments. By doing so, students gain invaluable coding experience.

Having access to experienced programmers can enhance a student’s understanding. These experts provide insights on writing efficient and clean code. They also offer guidance on debugging, improving a student’s problem-solving abilities.

“Do My Programming Homework” assistance typically includes:

Help with coding assignments in various programming languages

Support for integrating complex data structures and algorithms

Debugging and code optimization tips

Techniques for improving code efficiency and maintainability

Such services empower students to transition from mere theory to practical competence.

They also build confidence by allowing students to tackle challenging projects with expert support. Learning by doing enables students to retain concepts more effectively.

Ultimately, these services bridge the gap between theory and practice. They provide a practical learning experience that is crucial for mastering data structures and algorithms.

This practical grounding is essential for future academic and career success in computer science.

Enhancing Academic Performance and Confidence

Mastering data structures and algorithms can dramatically boost academic performance.

With assignment help, students receive personalized guidance, which directly impacts their grades. By achieving better results, students gain confidence in their skills and capabilities.

Assignment help services provide insights beyond textbooks, allowing students to excel.

Expert tutors clarify complex concepts, making learning accessible and engaging. This reduces anxiety associated with difficult coursework, allowing students to focus more effectively.

Increased confidence leads to more active classroom participation. Students feel better prepared to tackle new challenges and contribute to discussions. This positive feedback loop enhances their overall educational experience.

Ultimately, the knowledge gained through assignment help translates into long-term success.

By building a strong foundation in data structures and algorithms, students are better equipped for future studies and career paths.

Empowered by confidence and solid understanding, they are ready to tackle the ever-evolving world of computer science.

The Importance of 24/7 Support and Accessibility

Around-the-clock support is crucial for students in different time zones and with tight schedules.

Assignment help services offer 24/7 accessibility, ensuring students can get assistance whenever they need it. This flexibility is vital for accommodating busy lifestyles and urgent queries.

Many students juggle studies with part-time jobs or other responsibilities. Having access to expert help at any hour helps manage unexpected challenges.

Students can address doubts instantly without waiting for traditional office hours, making learning more efficient.

Immediate support also aids in maintaining a steady learning pace. Students can clarify issues as they arise, preventing misunderstandings from hindering their progress.

This continuous assistance cultivates a more structured and uninterrupted study routine.

Additionally, 24/7 support fosters a reliable learning environment. Students feel reassured knowing help is just a click away, no matter when or where they’re studying.

This assurance contributes to increased motivation and the perseverance needed to tackle demanding topics like data structures and algorithms.

Real-World Applications: Connecting Theory with Practice

Understanding data structures and algorithms isn’t just about passing exams. It’s about solving real-world problems efficiently.

These concepts form the backbone of all software applications, from basic calculators to complex artificial intelligence systems.

Bridging the gap between theory and practice can be challenging for many students.

Assignment help services play a crucial role by providing real-world examples that demonstrate these concepts in action. This hands-on approach makes abstract ideas more tangible and accessible.

The practical application of data structures and algorithms enhances a student’s ability to tackle real-life scenarios.

For instance, knowing how different algorithms optimize search and sort operations can lead to more efficient coding practices. Understanding these applications prepares students for future career opportunities.

Practical examples often include case studies that highlight the use of algorithms in various industries.

This exposure not only enriches understanding but also aligns academic learning with professional requirements.

As a result, students gain insight into potential career paths and the industries where their skills could be applied.

Here are some common real-world applications where data structures and algorithms are crucial:

Database management and query optimization

Network routing and data transmission

Search engines and information retrieval

E-commerce platforms and transaction processing

Machine learning and data analysis

Connecting theory with practice ensures students are prepared for the workforce. With assistance from assignment help services, they can apply their knowledge effectively and confidently in diverse fields.

Preparing for Technical Interviews and Career Advancement

Mastering data structures and algorithms is crucial for technical interviews. Companies often use these topics to evaluate candidates’ problem-solving skills and coding proficiency. Preparing for these interviews can be daunting without proper guidance.

Assignment help services offer valuable support for students aiming to excel in technical interviews. Experts can provide specific interview questions and scenarios that reflect real-world challenges. This targeted preparation enhances a student’s confidence and readiness.

Moreover, understanding different algorithms and their efficiencies aids in making informed decisions during an interview. Knowledge of various data structures allows candidates to demonstrate versatility and adaptability. This breadth of expertise makes them stand out in a competitive job market.

Assignment help can also offer insights into the latest industry trends and technologies. Staying updated is essential for career advancement in tech fields. With expert guidance, students can build a solid foundation that supports long-term success and development.

Choosing the Right Assignment Help Service

Selecting the right assignment help service is vital for effective learning. With numerous options available, it can be overwhelming. Focus on finding a service that aligns with your educational goals and needs.

Look for a service that offers qualified and experienced tutors. Experts should possess a deep understanding of data structures and algorithms. This ensures that you receive relevant and insightful guidance.

Consider the availability and flexibility of the service. A reliable service should offer 24/7 support to accommodate diverse schedules. Accessibility is key for students juggling multiple responsibilities.

Here’s a handy checklist to guide your choice:

Expertise and Qualification: Are the tutors experienced in data structures and algorithms?

Support and Availability: Is 24/7 support available for urgent help?

Reputation and Reviews: What do past clients say about their service?

Customization and Flexibility: Does the service tailor its approach to meet your needs?

Making an informed decision ensures that you receive the help necessary to master complex concepts effectively and efficiently.

Conclusion: Building a Strong Foundation for Future Success

Mastering data structures and algorithms is crucial for those pursuing a career in computer science. Assignment help offers personalized support and expert guidance, making it easier to grasp complex concepts.

Utilizing AssignmentDude assignment help services effectively bridges the gap between theory and practical application. It equips students with the skills necessary to tackle real-world challenges and enhances problem-solving abilities. Submit Your Assignment Now!

By investing in assignment help, students lay a solid foundation for academic achievement and professional growth. The knowledge gained can be a stepping stone to future success in technology-related fields.

FAQs About Assignment Help for Data Structures and Algorithms

What are the key benefits of assignment help services?

Assignment help provides expert guidance, ensuring students can better understand data structures and algorithms. It offers flexible support tailored to individual learning needs and schedules.

How does assignment help impact academic performance?

With professional assistance, students can improve their comprehension and grades. The help enhances time management, reduces stress, and contributes to higher academic achievements.

Is assignment help suitable for urgent assignments?

Yes, urgent assignment help services cater to tight deadlines. They provide rapid support, helping students complete tasks efficiently without compromising on quality.

By addressing these common questions, students can make informed decisions about using assignment help services. This support can play a significant role in their educational journey, ensuring they maximize their learning potential.

#do my programming homework #programming assignment help #urgent assignment help #assignment help service #final year project help #php assignment help #python programming

0 notes

fretzine · 11 months ago

Text

Space, Time and Good Code

It's been some time since I last posted to the blog. I've completed my third year studying BsC Computing and IT (Software Engineering)🎉.

In my last post I discussed the Data Structures and Algorithms module (M269) which, as predicted, was a beast. It would be a shame not to cover this module that is so integral to computer science and is genuinely quite interesting (i think so).

What makes some code better than others?

Over the years of trawling through forums and stack overflow I'd heard the term "bad code" and "good code" but it seemed like a subjective distinction that only the minds of the fashionistas of the programming world could make. What makes my code good? Is it the way it looks, how difficult it is to understand? Perhaps I'm using arrays and their using sets, what about string interpolation isntead of concatenation? As it turns out there is a very robust method of measuring the quality of code and it comes in the form of Complexity Analysis.

Complexity analysis is a method used in computer science to evaluate the efficiency of algorithms. It helps determine how the performance of an algorithm scales with the size of the input. By analyzing time and space complexity, we can predict how long an algorithm will take to run and how much memory it will use. This ensures that algorithms are optimized for different hardware and software environments, making them more efficient and practical for real-world applications.

Big O and Theta

Complexity analysis has its roots in the early days of computer science, evolving from the need to evaluate algorithm efficiency. In the 1960s and 1970s, pioneers like Donald Knuth and Robert Tarjan formalized methods to analyze algorithm performance, focusing on time and space complexity. This period saw the development of Big O notation, which became a standard for describing algorithm efficiency. Complexity theory further expanded with the introduction of classes like P and NP, exploring the boundaries of computational feasibility.

Big O notation describes the worst-case scenario for an algorithm, showing the maximum time it could take to complete. Think of it as the upper limit of how slow an algorithm can be. For example, if an algorithm is O(n), its time to complete grows linearly with the input size.

Big Theta notation, on the other hand, gives a more precise measure. It describes both the upper and lower bounds, meaning it shows the average or typical case. If an algorithm is Θ(n), its time to complete grows linearly with the input size, both in the best and worst case.

In complexity analysis, there are several types of complexity to consider:

Time Complexity: This measures how the runtime of an algorithm changes with the size of the input. It’s often expressed using Big O notation (e.g., O(n), O(log n)).

Space Complexity: This evaluates the amount of memory an algorithm uses relative to the input size. Like time complexity, it’s also expressed using Big O notation.

Worst-Case Complexity: This describes the maximum time or space an algorithm will require, providing an upper bound on its performance.

Best-Case Complexity: This indicates the minimum time or space an algorithm will need, representing the most optimistic scenario.

Average-Case Complexity: This gives an expected time or space requirement, averaging over all possible inputs.

There are also several different complexities.

Here are some common types of Big O complexities:

O(1) - Constant Time: The algorithm’s runtime does not change with the input size. Example: Accessing an element in an array.

O(n) - Linear Time: The runtime grows linearly with the input size. Example: Iterating through an array.

O(log n) - Logarithmic Time: The runtime grows logarithmically with the input size. Example: Binary search.

O(n log n) - Linearithmic Time: The runtime grows in proportion to ( n \log n ). Example: Merge sort.

O(n^2) - Quadratic Time: The runtime grows quadratically with the input size. Example: Bubble sort.

O(2^n) - Exponential Time: The runtime doubles with each additional input element. Example: Solving the traveling salesman problem using brute force.

O(n!) - Factorial Time: The runtime grows factorially with the input size.

Here's a diagram that shows the change in runtime for the different complexities:

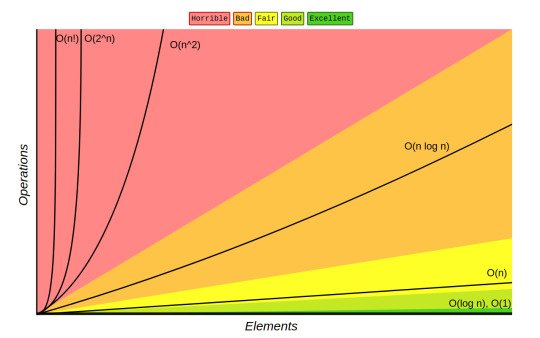
Data Structures to improve complexity

Throughout the M269 module you are introduced to a variety of data structures that help improve efficiency in several, very clever ways.

For example, suppose you have an array of numbers and you want to find a specific number. You would start at the beginning of the array and check each element one by one until you find the number or reach the end of the array. This process involves checking each element, so if the array has ( n ) elements, you might need to check up to ( n ) elements in the worst case.

Therefore, in its worse case scenario an array of 15 items will take 15 steps before realising that the value is not present in the array.

Here’s a simple code example in Python:

def linear_search(arr, target): for i in range(len(arr)): if arr[i] == target: return i return -1

You need to check each item in an array sequentially because the values at each index aren’t visible from the outside. Essentially, you have to look inside each “box” to see its value, which means manually opening each one in turn.

However, with a hash set, which creates key-value pairs for each element, the process becomes much more efficient!

A hash set is a data structure that stores unique elements using a mechanism called hashing. Each element is mapped to a unique hash code, which determines its position in the set. This allows for constant time complexity, O(1), for basic operations like add, remove, and contains, assuming a good hash function. This efficiency is because the hash code directly points to the location of the element, eliminating the need for a linear search. As a result, hash sets significantly improve search performance compared to arrays or lists, especially with large datasets.

This is just one of the many data structures that we learned can help improve complexity. Some others we look at are:

Stacks

Queues

Linked List

Trees

Graphs

Better Algorithms!

Yes, data structures can dramatically improve the efficiency of your algorithms but algorithm design is the other tool in your arsenal.

Algorithm design is crucial in improving efficiency because it directly impacts the performance and scalability of software systems. Well-designed algorithms ensure that tasks are completed in the shortest possible time and with minimal resource usage.

An example of algorithm design that dramatically improves efficiency is Binary Search.

Binary search is an efficient algorithm for finding a target value within a sorted array. It works by repeatedly dividing the search interval in half until the target value is found or the interval is empty.

Here’s how it works:

Start with the entire array: Identify the middle element.

Compare the middle element: If it matches the target value, the search is complete.

Adjust the search interval: If the target is smaller than the middle element, focus on the left half of the array. If it’s larger, focus on the right half.

Repeat: Continue this process until the target is found or the interval is empty.

Example: Suppose you have a sorted array ([2, 5, 8, 12, 16, 23, 38, 56, 72, 91]) and you want to find the number 23. Start by comparing 23 with the middle element (23). Since they match, the search ends successfully.

Here is an image of a Binary Search algorithm being applied to a Rooted Tree (a graph with a root node):

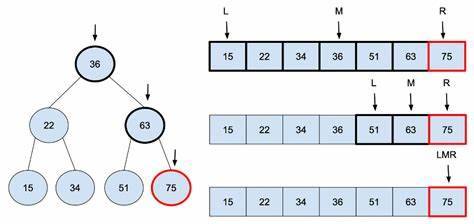
Complexity Improvement: Binary search significantly improves search efficiency compared to linear search. While linear search has a time complexity of O(n), binary search has a time complexity of O(log n). This logarithmic growth means that even for large datasets, the number of comparisons needed is relatively small. For example, in an array of 1,000,000 elements, binary search would require at most about 20 comparisons, whereas linear search might need up to 1,000,000 comparisons.

What on earth am i going on about?

Like I said, last year I wouldn't have been able to discern good code from bad code. Now I can analyse the complexity of a piece of code and determine its efficiency, especially as its input grows. I can also see if the programmer has used efficient data structures in their code, rather than bog standard arrays (arrays are amazing btw, no hate).

Ultimately, I feel like this module has definitely made me a better programmer.

#computing #yearthree #data structures #algorithms #programming #technology #tech #dev #web dev

0 notes

myprogrammingsolver · 1 year ago

Text

P05 Simple Benchmarking-Solved

Overview Analyzing runtime complexity of a program can, as you’re learning this week, take the form of a theoretical analysis expressed in Big-O notation and mathematical formulas, but it can also be a more informal measure of “how long does this program take to run on controlled inputs?” Broadly, this timed version is called benchmarking. There are many advanced tools for profiling system usage…

View On WordPress

0 notes

akshayroy123 · 2 years ago

Text

What is Time Complexity And Why Is It Essential?

In the world of computer science and algorithms, there is a crucial concept that reigns supreme when it comes to evaluating the efficiency of algorithms: time complexity. Time complexity is the measure of how an algorithm's execution time grows with respect to the size of its input data. It is essential because it allows us to compare and analyze different algorithms' performance objectively. In this article, we will delve into the concept of time complexity, its significance, and why it is essential in the field of computer science. So, let’s get started with some Technical Training Program ahead.

Understanding Time Complexity

Time complexity is a fundamental concept in computer science that helps us quantify the amount of time an algorithm takes to run as a function of the input size. It provides us with a clear and systematic way to analyze and compare the efficiency of algorithms. Time complexity is typically expressed using big O notation, which describes the upper bound of an algorithm's running time concerning its input size. For instance, O(n) represents linear time complexity, indicating that an algorithm's execution time grows linearly with the size of the input.

Importance of Time Complexity

Algorithm Selection:

Time complexity is essential for choosing the most suitable algorithm for a specific task. When faced with multiple algorithms to solve a problem, analyzing their time complexities helps us select the one that will perform the best in practice, thanks to Technical Transformation and evolution. An algorithm with a lower time complexity is more efficient and preferable.

Resource Allocation:

In many real-world applications, computational resources like CPU time and memory are limited. Time complexity guides us in making informed decisions about resource allocation. Algorithms with low time complexity are preferred in resource-constrained environments, ensuring that the system operates efficiently.

Scalability:

As the volume of data processed by computers continues to grow, scalability becomes a critical concern. Time complexity helps us assess how well an algorithm can oversee larger datasets. Algorithms with lower time complexity are more scalable, making them suitable for big data applications.

Optimization:

Time complexity analysis is a vital tool in optimizing algorithms. By identifying bottlenecks and inefficiencies in an algorithm's code, developers can work to improve its performance. This process often involves reducing time complexity, resulting in faster and more efficient algorithms.

Predictability:

Time complexity allows us to predict an algorithm's behavior under different conditions. It helps us estimate how long an algorithm will take to execute, making it valuable for designing real-time systems and meeting performance requirements followed by in-depth Technical Learning.

Real-World Applications

Time complexity is not just an abstract concept; it plays a crucial role in various real-world applications:

Search Engines:

Search engines like Google process enormous amounts of data in real-time which is a perk of the evolving Technical Transformation. The algorithms used for ranking and retrieving search results rely on efficient data structures and algorithms with low time complexity to deliver fast and relevant results.

E-commerce:

Online shopping platforms use algorithms to recommend products to users based on their browsing and purchase history. These recommendation algorithms must process vast datasets efficiently, making time complexity analysis indispensable.

Financial Trading:

High-frequency trading systems execute thousands of trades per second. Time complexity is vital for optimizing trading algorithms to gain a competitive edge in the financial markets. Relevant Technical Training Courses can give us more knowledge of this.

Healthcare:

Medical imaging and diagnostic algorithms must process and analyze large datasets, often in time-critical situations. Low time complexity is essential for providing timely and accurate results.

Final Words

Time complexity is a fundamental concept in computer science that enables us to evaluate and compare the efficiency of algorithms. It plays a crucial role in algorithm selection, resource allocation, scalability, optimization, and predictability. In a world where computational power is at the heart of technological advancements, understanding and leveraging time complexity is essential for designing and implementing efficient algorithms that drive innovation and solve complex problems.

Moreover, relevant Technical Training Courses should also be made available for employees to enhance their skills and efficiency. As technology continues to evolve, the significance of highly skilled employees in the workplace along with time complexity in the field of computer science remains unwavering, making it a cornerstone of algorithmic efficiency.

#Technical Training Program #Technical Transformation #Technical Training Courses

0 notes

toneophealthandfitness · 2 years ago

Text

How Can DC Analysis Help Us Understand How Algorithms Act And Perform

A valuable technique for algorithmic evaluation, DC analysis allows for a thorough understanding of algorithm behaviour and performance. The Design of Algorithms' DC examination of algorithmic dynamics under various conditions sheds light on algorithms' effectiveness, scalability, and efficiency, enabling programmers to optimise and improve algorithms for better results.

Algorithm efficiency and effectiveness can be improved by optimisation and fine-tuning when using DC analysis in the design of algorithms.

A Summary Of DC Analysis

Understanding how algorithms behave and function is made easier with DC analysis, sometimes called Design and Control analysis. DC analysis offers insights into an algorithm's inner workings by methodically analysing distinct algorithmic elements and their relationships.

Algorithm designers can examine the complexity, resource needs, and execution time of various algorithmic operations through DC analysis.

Using DC Analysis When Creating Algorithms

1. Improvement

By locating and eliminating design flaws and bottlenecks, DC analysis aids in software engineering by optimising the performance and efficiency of algorithms.

2. Component Assessment

It enables designers to make knowledgeable design decisions by permitting a thorough evaluation of algorithmic elements, their interactions, and resource requirements.

3. Parameter Adjustment

Adjusting parameters to attain the best algorithm performance for various input sizes and conditions is made easier with the help of DC analysis.

4. Scalability Evaluation

It assists in determining potential constraints and assuring resilience across multiple data sets and computational contexts while also evaluating the scalability of algorithms.

5. Prediction Of Resource

By researching algorithm activity through DC analysis, designers can estimate resource requirements, such as memory and processing power, enabling optimal resource allocation.

Essential Points About Designing Algorithms Effective Algorithm Design Requires

Understanding the problem, breaking it down into manageable components, data structures, algorithmic paradigms, complexity analysis, iterative improvement, and documentation. All of these elements work together to produce trustworthy and practical algorithms.

1. Problem Recognition

With a thorough understanding of the problem at hand, including its objectives, constraints, and input/output requirements, algorithm creation can proceed.

2. Disintegration

Making the challenge into smaller, more manageable subproblems makes the design process more accessible and possible to build solutions step-by-step.

3.Data Structures

Choosing suitable data structures is essential for designing efficient algorithms. The choice is dependent on the characteristics of the issue, such as the organisation of the data, access patterns, and required actions.

4. Statistical Models

Different algorithmic paradigms offer frameworks used in network programming for creating practical solutions based on problem-specific characteristics, such as divide-and-conquer dynamic programming or greedy algorithms.

5. Analysis Of Time And Space Complexity

The efficiency and scalability of the algorithm can be evaluated by looking at its time and space complexity, allowing designers to maximise performance.

Essential Points For Algorithm Analysis

One can thoroughly understand an algorithm's performance characteristics and make educated decisions about its suitability for particular applications by thoroughly analysing algorithms, including time and space complexity evaluation, using Big O notation, considering various scenarios, and validating through experiments.

1.Timing Complexity

Analysing how an algorithm execution time scales concerning the input size allows for the efficiency of the method to be evaluated.

2.The Complexity Of Space

Measuring the amount of memory an algorithm uses while running and considering variables, data structures, and recursion depth are all part of analysing an algorithm's space complexity.

3.Big O Notation

Big O notation provides a defined way to compare and categorise algorithms based on their effectiveness by expressing the upper bound of an algorithm's time or space complexity.

4. Analysis Of The Best Case, Worst Case, And Average Case

The algorithm's performance under diverse inputs may be understood, and its behaviour can be better understood by considering various scenarios.

5.Asymptotic Analysis

As the input size approaches infinity, the asymptotic analysis concentrates on the increased rate of the algorithm's time or space complexity, allowing for comparisons of effectiveness across various input sizes.

The Term "Fundamental Algorithms" Is Confusing

The term "fundamental algorithms" refers to the essential group of algorithms that form the basis of computer science and the use of computation to solve problems.

A variety of algorithmic methods and approaches to problem-solving are included in fundamental algorithms. These include well-known algorithms for operations like sorting (Quicksort, Merge sort), searching (Binary search), traversing a graph (Depth-First Search, Breadth-First Search), and dynamic programming (Fibonacci sequence computation), among others.

Design And Analysis Of Fundamental Algorithms

Developers can build foundational algorithms that are effective at tackling various computing problems by implementing these design and analytical concepts.

1. Problem Recognition

Understanding the needs, limitations, and intended outcomes of the problem is the first step in designing fundamental algorithms.

2. Methods For Designing Algorithms

Various algorithm design strategies, including divide-and-conquer greedy algorithms and dynamic programming, are used to develop effective and ideal solutions.

3. Analysis Of Time And Space Complexity

Fundamental algorithms' time and space complexity can be examined to assess their effectiveness and scalability and provide insights into their performance characteristics.

4. Algorithm Accuracy

To ensure that fundamental algorithms provide accurate and trustworthy results, it is essential to ensure their correctness, frequently through formal proofs or in-depth testing.

5. Strategies For Optimisation

Fundamental algorithm optimization entails locating bottlenecks, eliminating pointless computations, and increasing algorithmic effectiveness through algorithmic tweaks or data structure selections.

About BGI

The Bansal Group of Institutes offers various engineering, management, and nursing courses. It has the best and top-placement colleges in its various campuses across Bhopal, Indore, and Mandideep. With credible faculty and well-equipped laboratories, BGI ensures a top-notch learning experience.

Visit Our Websites

Bhopal- https://bgibhopal.com/

Indore- https://sdbc.ac.in/Mandideep- https://bce.ac.in/ Click on the link to get yourself registered- https://bgibhopal.com/registration-form/

0 notes

courseforfree · 4 years ago

Link

Data Structures and Algorithms from Zero to Hero and Crack Top Companies 100+ Interview questions (Java Coding)

What you’ll learn

Java Data Structures and Algorithms Masterclass

Learn, implement, and use different Data Structures

Learn, implement and use different Algorithms

Become a better developer by mastering computer science fundamentals

Learn everything you need to ace difficult coding interviews

Cracking the Coding Interview with 100+ questions with explanations

Time and Space Complexity of Data Structures and Algorithms

Recursion

Big O

Dynamic Programming

Divide and Conquer Algorithms

Graph Algorithms

Greedy Algorithms

Requirements

Basic Java Programming skills

Description

Welcome to the Java Data Structures and Algorithms Masterclass, the most modern, and the most complete Data Structures and Algorithms in Java course on the internet.

At 44+ hours, this is the most comprehensive course online to help you ace your coding interviews and learn about Data Structures and Algorithms in Java. You will see 100+ Interview Questions done at the top technology companies such as Apple, Amazon, Google, and Microsoft and how-to face Interviews with comprehensive visual explanatory video materials which will bring you closer to landing the tech job of your dreams!

Learning Java is one of the fastest ways to improve your career prospects as it is one of the most in-demand tech skills! This course will help you in better understanding every detail of Data Structures and how algorithms are implemented in high-level programming languages.

We’ll take you step-by-step through engaging video tutorials and teach you everything you need to succeed as a professional programmer.

After finishing this course, you will be able to:

Learn basic algorithmic techniques such as greedy algorithms, binary search, sorting, and dynamic programming to solve programming challenges.

Learn the strengths and weaknesses of a variety of data structures, so you can choose the best data structure for your data and applications

Learn many of the algorithms commonly used to sort data, so your applications will perform efficiently when sorting large datasets

Learn how to apply graph and string algorithms to solve real-world challenges: finding shortest paths on huge maps and assembling genomes from millions of pieces.

Why this course is so special and different from any other resource available online?

This course will take you from the very beginning to very complex and advanced topics in understanding Data Structures and Algorithms!

You will get video lectures explaining concepts clearly with comprehensive visual explanations throughout the course.

You will also see Interview Questions done at the top technology companies such as Apple, Amazon, Google, and Microsoft.

I cover everything you need to know about the technical interview process!

So whether you are interested in learning the top programming language in the world in-depth and interested in learning the fundamental Algorithms, Data Structures, and performance analysis that make up the core foundational skillset of every accomplished programmer/designer or software architect and is excited to ace your next technical interview this is the course for you!

And this is what you get by signing up today:

Lifetime access to 44+ hours of HD quality videos. No monthly subscription. Learn at your own pace, whenever you want

Friendly and fast support in the course Q&A whenever you have questions or get stuck

FULL money-back guarantee for 30 days!

This course is designed to help you to achieve your career goals. Whether you are looking to get more into Data Structures and Algorithms, increase your earning potential, or just want a job with more freedom, this is the right course for you!

The topics that are covered in this course.

Section 1 – Introduction

What are Data Structures?

What is an algorithm?

Why are Data Structures And Algorithms important?

Types of Data Structures

Types of Algorithms

Section 2 – Recursion

What is Recursion?

Why do we need recursion?

How does Recursion work?

Recursive vs Iterative Solutions

When to use/avoid Recursion?

How to write Recursion in 3 steps?

How to find Fibonacci numbers using Recursion?

Section 3 – Cracking Recursion Interview Questions

Question 1 – Sum of Digits

Question 2 – Power

Question 3 – Greatest Common Divisor

Question 4 – Decimal To Binary

Section 4 – Bonus CHALLENGING Recursion Problems (Exercises)

power

factorial

products array

recursiveRange

fib

reverse

palindrome

some recursive

flatten

capitalize first

nestedEvenSum

capitalize words

stringifyNumbers

collects things

Section 5 – Big O Notation

Analogy and Time Complexity

Big O, Big Theta, and Big Omega

Time complexity examples

Space Complexity

Drop the Constants and the nondominant terms

Add vs Multiply

How to measure the codes using Big O?

How to find time complexity for Recursive calls?

How to measure Recursive Algorithms that make multiple calls?

Section 6 – Top 10 Big O Interview Questions (Amazon, Facebook, Apple, and Microsoft)

Product and Sum

Print Pairs

Print Unordered Pairs

Print Unordered Pairs 2 Arrays

Print Unordered Pairs 2 Arrays 100000 Units

Reverse

O(N) Equivalents

Factorial Complexity

Fibonacci Complexity

Powers of 2

Section 7 – Arrays

What is an Array?

Types of Array

Arrays in Memory

Create an Array

Insertion Operation

Traversal Operation

Accessing an element of Array

Searching for an element in Array

Deleting an element from Array

Time and Space complexity of One Dimensional Array

One Dimensional Array Practice

Create Two Dimensional Array

Insertion – Two Dimensional Array

Accessing an element of Two Dimensional Array

Traversal – Two Dimensional Array

Searching for an element in Two Dimensional Array

Deletion – Two Dimensional Array

Time and Space complexity of Two Dimensional Array

When to use/avoid array

Section 8 – Cracking Array Interview Questions (Amazon, Facebook, Apple, and Microsoft)

Question 1 – Missing Number

Question 2 – Pairs

Question 3 – Finding a number in an Array

Question 4 – Max product of two int

Question 5 – Is Unique

Question 6 – Permutation

Question 7 – Rotate Matrix

Section 9 – CHALLENGING Array Problems (Exercises)

Middle Function

2D Lists

Best Score

Missing Number

Duplicate Number

Pairs

Section 10 – Linked List

What is a Linked List?

Linked List vs Arrays

Types of Linked List

Linked List in the Memory

Creation of Singly Linked List

Insertion in Singly Linked List in Memory

Insertion in Singly Linked List Algorithm

Insertion Method in Singly Linked List

Traversal of Singly Linked List

Search for a value in Single Linked List

Deletion of a node from Singly Linked List

Deletion Method in Singly Linked List

Deletion of entire Singly Linked List

Time and Space Complexity of Singly Linked List

Section 11 – Circular Singly Linked List

Creation of Circular Singly Linked List

Insertion in Circular Singly Linked List

Insertion Algorithm in Circular Singly Linked List

Insertion method in Circular Singly Linked List

Traversal of Circular Singly Linked List

Searching a node in Circular Singly Linked List

Deletion of a node from Circular Singly Linked List

Deletion Algorithm in Circular Singly Linked List

A method in Circular Singly Linked List

Deletion of entire Circular Singly Linked List

Time and Space Complexity of Circular Singly Linked List

Section 12 – Doubly Linked List

Creation of Doubly Linked List

Insertion in Doubly Linked List

Insertion Algorithm in Doubly Linked List

Insertion Method in Doubly Linked List

Traversal of Doubly Linked List

Reverse Traversal of Doubly Linked List

Searching for a node in Doubly Linked List

Deletion of a node in Doubly Linked List

Deletion Algorithm in Doubly Linked List

Deletion Method in Doubly Linked List

Deletion of entire Doubly Linked List

Time and Space Complexity of Doubly Linked List

Section 13 – Circular Doubly Linked List

Creation of Circular Doubly Linked List

Insertion in Circular Doubly Linked List

Insertion Algorithm in Circular Doubly Linked List

Insertion Method in Circular Doubly Linked List

Traversal of Circular Doubly Linked List

Reverse Traversal of Circular Doubly Linked List

Search for a node in Circular Doubly Linked List

Delete a node from Circular Doubly Linked List

Deletion Algorithm in Circular Doubly Linked List

Deletion Method in Circular Doubly Linked List

Entire Circular Doubly Linked List

Time and Space Complexity of Circular Doubly Linked List

Time Complexity of Linked List vs Arrays

Section 14 – Cracking Linked List Interview Questions (Amazon, Facebook, Apple, and Microsoft)

Linked List Class

Question 1 – Remove Dups

Question 2 – Return Kth to Last

Question 3 – Partition

Question 4 – Sum Linked Lists

Question 5 – Intersection

Section 15 – Stack

What is a Stack?

What and Why of Stack?

Stack Operations

Stack using Array vs Linked List

Stack Operations using Array (Create, isEmpty, isFull)

Stack Operations using Array (Push, Pop, Peek, Delete)

Time and Space Complexity of Stack using Array

Stack Operations using Linked List

Stack methods – Push, Pop, Peek, Delete, and isEmpty using Linked List

Time and Space Complexity of Stack using Linked List

When to Use/Avoid Stack

Stack Quiz

Section 16 – Queue

What is a Queue?

Linear Queue Operations using Array

Create, isFull, isEmpty, and enQueue methods using Linear Queue Array

Dequeue, Peek and Delete Methods using Linear Queue Array

Time and Space Complexity of Linear Queue using Array

Why Circular Queue?

Circular Queue Operations using Array

Create, Enqueue, isFull and isEmpty Methods in Circular Queue using Array

Dequeue, Peek and Delete Methods in Circular Queue using Array

Time and Space Complexity of Circular Queue using Array

Queue Operations using Linked List

Create, Enqueue and isEmpty Methods in Queue using Linked List

Dequeue, Peek and Delete Methods in Queue using Linked List

Time and Space Complexity of Queue using Linked List

Array vs Linked List Implementation

When to Use/Avoid Queue?

Section 17 – Cracking Stack and Queue Interview Questions (Amazon, Facebook, Apple, Microsoft)

Question 1 – Three in One

Question 2 – Stack Minimum

Question 3 – Stack of Plates

Question 4 – Queue via Stacks

Question 5 – Animal Shelter

Section 18 – Tree / Binary Tree

What is a Tree?

Why Tree?

Tree Terminology

How to create a basic tree in Java?

Binary Tree

Types of Binary Tree

Binary Tree Representation

Create Binary Tree (Linked List)

PreOrder Traversal Binary Tree (Linked List)

InOrder Traversal Binary Tree (Linked List)

PostOrder Traversal Binary Tree (Linked List)

LevelOrder Traversal Binary Tree (Linked List)

Searching for a node in Binary Tree (Linked List)

Inserting a node in Binary Tree (Linked List)

Delete a node from Binary Tree (Linked List)

Delete entire Binary Tree (Linked List)

Create Binary Tree (Array)

Insert a value Binary Tree (Array)

Search for a node in Binary Tree (Array)

PreOrder Traversal Binary Tree (Array)

InOrder Traversal Binary Tree (Array)

PostOrder Traversal Binary Tree (Array)

Level Order Traversal Binary Tree (Array)

Delete a node from Binary Tree (Array)

Entire Binary Tree (Array)

Linked List vs Python List Binary Tree

Section 19 – Binary Search Tree

What is a Binary Search Tree? Why do we need it?

Create a Binary Search Tree

Insert a node to BST

Traverse BST

Search in BST

Delete a node from BST

Delete entire BST

Time and Space complexity of BST

Section 20 – AVL Tree

What is an AVL Tree?

Why AVL Tree?

Common Operations on AVL Trees

Insert a node in AVL (Left Left Condition)

Insert a node in AVL (Left-Right Condition)

Insert a node in AVL (Right Right Condition)

Insert a node in AVL (Right Left Condition)

Insert a node in AVL (all together)

Insert a node in AVL (method)

Delete a node from AVL (LL, LR, RR, RL)

Delete a node from AVL (all together)

Delete a node from AVL (method)

Delete entire AVL

Time and Space complexity of AVL Tree

Section 21 – Binary Heap

What is Binary Heap? Why do we need it?

Common operations (Creation, Peek, sizeofheap) on Binary Heap

Insert a node in Binary Heap

Extract a node from Binary Heap

Delete entire Binary Heap

Time and space complexity of Binary Heap

Section 22 – Trie

What is a Trie? Why do we need it?

Common Operations on Trie (Creation)

Insert a string in Trie

Search for a string in Trie

Delete a string from Trie

Practical use of Trie

Section 23 – Hashing

What is Hashing? Why do we need it?

Hashing Terminology

Hash Functions

Types of Collision Resolution Techniques

Hash Table is Full

Pros and Cons of Resolution Techniques

Practical Use of Hashing

Hashing vs Other Data structures

Section 24 – Sort Algorithms

What is Sorting?

Types of Sorting

Sorting Terminologies

Bubble Sort

Selection Sort

Insertion Sort

Bucket Sort

Merge Sort

Quick Sort

Heap Sort

Comparison of Sorting Algorithms

Section 25 – Searching Algorithms

Introduction to Searching Algorithms

Linear Search

Linear Search in Python

Binary Search

Binary Search in Python

Time Complexity of Binary Search

Section 26 – Graph Algorithms

What is a Graph? Why Graph?

Graph Terminology

Types of Graph

Graph Representation

The graph in Java using Adjacency Matrix

The graph in Java using Adjacency List

Section 27 – Graph Traversal

Breadth-First Search Algorithm (BFS)

Breadth-First Search Algorithm (BFS) in Java – Adjacency Matrix

Breadth-First Search Algorithm (BFS) in Java – Adjacency List

Time Complexity of Breadth-First Search (BFS) Algorithm

Depth First Search (DFS) Algorithm

Depth First Search (DFS) Algorithm in Java – Adjacency List

Depth First Search (DFS) Algorithm in Java – Adjacency Matrix

Time Complexity of Depth First Search (DFS) Algorithm

BFS Traversal vs DFS Traversal

Section 28 – Topological Sort

What is Topological Sort?

Topological Sort Algorithm

Topological Sort using Adjacency List

Topological Sort using Adjacency Matrix

Time and Space Complexity of Topological Sort

Section 29 – Single Source Shortest Path Problem

what is Single Source Shortest Path Problem?

Breadth-First Search (BFS) for Single Source Shortest Path Problem (SSSPP)

BFS for SSSPP in Java using Adjacency List

BFS for SSSPP in Java using Adjacency Matrix

Time and Space Complexity of BFS for SSSPP

Why does BFS not work with Weighted Graph?

Why does DFS not work for SSSP?

Section 30 – Dijkstra’s Algorithm

Dijkstra’s Algorithm for SSSPP

Dijkstra’s Algorithm in Java – 1

Dijkstra’s Algorithm in Java – 2

Dijkstra’s Algorithm with Negative Cycle

Section 31 – Bellman-Ford Algorithm

Bellman-Ford Algorithm

Bellman-Ford Algorithm with negative cycle

Why does Bellman-Ford run V-1 times?

Bellman-Ford in Python

BFS vs Dijkstra vs Bellman Ford

Section 32 – All Pairs Shortest Path Problem

All pairs shortest path problem

Dry run for All pair shortest path

Section 33 – Floyd Warshall

Floyd Warshall Algorithm

Why Floyd Warshall?

Floyd Warshall with negative cycle,

Floyd Warshall in Java,

BFS vs Dijkstra vs Bellman Ford vs Floyd Warshall,

Section 34 – Minimum Spanning Tree

Minimum Spanning Tree,

Disjoint Set,

Disjoint Set in Java,

Section 35 – Kruskal’s and Prim’s Algorithms

Kruskal Algorithm,

Kruskal Algorithm in Python,

Prim’s Algorithm,

Prim’s Algorithm in Python,

Prim’s vs Kruskal

Section 36 – Cracking Graph and Tree Interview Questions (Amazon, Facebook, Apple, Microsoft)

Section 37 – Greedy Algorithms

What is a Greedy Algorithm?

Well known Greedy Algorithms

Activity Selection Problem

Activity Selection Problem in Python

Coin Change Problem

Coin Change Problem in Python

Fractional Knapsack Problem

Fractional Knapsack Problem in Python

Section 38 – Divide and Conquer Algorithms

What is a Divide and Conquer Algorithm?

Common Divide and Conquer algorithms

How to solve the Fibonacci series using the Divide and Conquer approach?

Number Factor

Number Factor in Java

House Robber

House Robber Problem in Java

Convert one string to another

Convert One String to another in Java

Zero One Knapsack problem

Zero One Knapsack problem in Java

Longest Common Sequence Problem

Longest Common Subsequence in Java

Longest Palindromic Subsequence Problem

Longest Palindromic Subsequence in Java

Minimum cost to reach the Last cell problem

Minimum Cost to reach the Last Cell in 2D array using Java

Number of Ways to reach the Last Cell with given Cost

Number of Ways to reach the Last Cell with given Cost in Java

Section 39 – Dynamic Programming

What is Dynamic Programming? (Overlapping property)

Where does the name of DC come from?

Top-Down with Memoization

Bottom-Up with Tabulation

Top-Down vs Bottom Up

Is Merge Sort Dynamic Programming?

Number Factor Problem using Dynamic Programming

Number Factor: Top-Down and Bottom-Up

House Robber Problem using Dynamic Programming

House Robber: Top-Down and Bottom-Up

Convert one string to another using Dynamic Programming

Convert String using Bottom Up

Zero One Knapsack using Dynamic Programming

Zero One Knapsack – Top Down

Zero One Knapsack – Bottom Up

Section 40 – CHALLENGING Dynamic Programming Problems

Longest repeated Subsequence Length problem

Longest Common Subsequence Length problem

Longest Common Subsequence problem

Diff Utility

Shortest Common Subsequence problem

Length of Longest Palindromic Subsequence

Subset Sum Problem

Egg Dropping Puzzle

Maximum Length Chain of Pairs

Section 41 – A Recipe for Problem Solving

Introduction

Step 1 – Understand the problem

Step 2 – Examples

Step 3 – Break it Down

Step 4 – Solve or Simplify

Step 5 – Look Back and Refactor

Section 41 – Wild West

Download

To download more paid courses for free visit course catalog where 1000+ paid courses available for free. You can get the full course into your device with just a single click. Follow the link above to download this course for free.

3 notes · View notes

nvjkmr · 6 years ago

Text

Prerequisites I - DS 101

Abstract Data Type

An abstract piece of code that is re-usable and serves the purpose by hiding the inner workings of it and only exposing the interface for generic usage is known as an abstract data type.

For example, a user who needs to implement a railway booking engine to serve the user requests based on first-in, first-out (FIFO) method, will have to implement the queue for the specific use-case with operations such as enqueue & dequeue. The disadvantage of this approach is that the queue will have to be reimplemented for other use-cases that simulate the queue. This can be solved by having an abstract data type queue which implements the basic functionality (operations) of the queue and can be imported anywhere else it is required.

An abstract data type (ADT) can be thought of as a data declaration packaged along with the operations that are meaningful for the data.

ADT Implementations

Most data is required to be stored as either as linear or as a non-linear structure. An example of a linear and non-linear data structure would be an array and a tree respectively.

We have two basic structures to implement complex ADT list (both linear and non-linear): arrays and linked-lists.

Arrays can be used to store sequential data, where the data in a specific cell can be accessed efficiently if the index (address) is known, but it is very inefficient to add or remove new/existing elements. On the other hand, linked-lists do us a great favor in efficiently adding and removing nodes (atomic units of linked-lists), but are inefficient at accessing a node directly.

Node: It is a data structure that has a data part and link part (holds multiple links if it is non-linear), pointing to the next element(s).

Analysis of Algorithms

When there are no loops in a program (it is linear, which means it is a set of instructions), the efficiency of the program directly depends on the speed of the CPU. Hence, algorithm analysis focuses mostly on the loops (given that recursion can always be converted to a loop). The efficiency of a program (or an algorithm) is always a function of the number of elements to be processed/accessed.

Example:

n = 11 for i in range(n): # will create a list of numbers from 0 to 10 for j in range(i): # some code here return

The above code would run 55 times, as the inner loop would be a dependant on the value of i for each ith loop. When the value of i is 0, the inner loop runs 0 times, when i is 1, the inner loop runs 1 times and so on till the value of i is 10. If we choose the see the pattern, it would basically be: 1 + 2 + 3 + ... + 10. And if we consider it as a function of n, then: f(n) = n*(n+1)/2.

Big-O Notation

It is a notation to describe/represent the worst case runtime of an algorithm. The Big-O, as in "on the order of" is an approximate measure of efficiency and since it is only an estimate, we can focus only on the dominant factor in the equation.

Considering the previous example, the worst case scenario would be O(n^2).

Significance and other notations.

There are other notations of different measures of efficiency such as the theta notation and the omega notation. As with the Big-O notation defines the upper bound of the function, the omega function defines the lower bound or the best case runtime.

The theta notation is basically a function with 2 constants, where one represents an upper bound and the other represents the lower bound. Given a function f(n), there exists k and K such that n*k

#data structures 101

2 notes · View notes

cacmsinsitute · 2 years ago

Text

The Importance of Data Structures and Algorithms in Efficient Programming

Efficient programming is at the foundation of developing high-performance software applications. Understanding the importance of data structures and algorithms is an important component of gaining efficiency. In this post, we will look at the importance of data structures and algorithms in programming and how they contribute to optimized and faster code execution.

Understanding Data Structures: Data structures are the building blocks used to organize and store data in computer memory. They make it possible to efficiently represent and modify data. Discuss data structures such as arrays, linked lists, stacks, queues, trees, and graphs. Explain their properties, use cases, and supported operations. Emphasize the necessity of picking the suitable data structure depending on the problem needs.

Exploring Algorithms: Algorithms are step-by-step procedures or approaches for addressing issues. They define a series of instructions that turn incoming data into the intended output. Discuss common algorithmic approaches like searching, sorting, recursion, and dynamic programming. Explain their temporal and spatial difficulties and provide instances of their practical uses.

Optimizing Time Complexity: Time complexity refers to how long it takes an algorithm to perform as a function of input size. Explain the Big O notation and its use to time complexity analysis. Discuss time-saving measures such as applying efficient algorithms, optimizing loops, and creating appropriate data structures. Show how selecting the proper algorithm can significantly improve runtime.

Maximizing Space Efficiency: Space complexity refers to the amount of memory required by an algorithm to run as a function of input size. Explain how to analyze and optimize space complexity using ideas such as auxiliary space and in-place algorithms. Highlight the trade-offs between time and space efficiency, as well as how choosing the proper data structure might affect memory utilization.

Real-World Applications: Highlight real-world instances in which efficient data structures and algorithms are crucial. Discuss their function in large-scale data processing, network optimisation, image processing, and machine learning methods, for example. Showcase success stories in which organizations improved their performance significantly by optimizing data structures and algorithms.

Tools and Resources: Provide a list of popular programming languages, libraries, and frameworks with built-in data structures and algorithms. Mention online sites, books, and classes where programmers can improve their understanding and practical implementation skills.

Conclusion: Data structures and algorithms are critical pillars of efficient programming. Developers can optimize code execution, boost performance, and efficiently solve complicated problems by selecting the correct data structure and applying efficient algorithms. In order to stay up to speed with the newest breakthroughs in data structures and algorithms for efficient programming, emphasize the need of continual learning and experimenting.

Programmers can design software that scalable, performs effectively, and provides an amazing user experience by writing well-optimized code based on a strong understanding of data structures and algorithms.

Are you ready to improve your programming skills and learn more about data structures and algorithms? Join the Center for Advanced Computer And Management Studies (CACMS) today! Gain access to expert-led courses, hands-on workshops, and a friendly programming community. Increase the efficiency of your programming. Join CACMS today to maximize your potential in efficient programming! Contact +91 8288040281 or Visit http://cacms.in/Programming-Language/ for more Information.

#cacms institute #programming #programming Institute in Amritsar #programming tips and tricks #programming course #programming training course #programming classes near me #best institute for programming

0 notes

data-structures-cheat-she6h · 3 years ago

Text

data structures cheat sheet work ZSQF+

💾 ►►► DOWNLOAD FILE 🔥🔥🔥🔥🔥 We summarize the performance characteristics of classic algorithms and data structures for sorting, priority queues, symbol tables, and graph. This cheat sheet uses Big O notation to express time complexity. For a reminder on Big O, see Understanding Big O Notation and Algorithmic Complexity. Know Thy Complexities! · Big-O Complexity Chart · Common Data Structure Operations · Array Sorting Algorithms · Learn More · Get the Official Big-O Cheat Sheet. GitHub - tajpouria/algorithms-and-data-structures-cheat-sheet: A brief overview of common algorithms, data structures, and problem-solving patterns. 9 Algorithms and Data Structures Cheatsheet We summarize the performance characteristics of classic algorithms and data structures for sorting, priority queues, symbol tables, and graph processing. We also summarize some of the mathematics useful in the analysis of algorithms, including commonly encountered functions; useful formulas and approximations; properties of logarithms; asymptotic notations; and solutions to divide-and-conquer recurrences. The table below summarizes the number of compares for a variety of sorting algorithms, as implemented in this textbook. It includes leading constants but ignores lower-order terms. The table below summarizes the order of growth of the running time of operations for a variety of priority queues, as implemented in this textbook. It ignores leading constants and lower-order terms. Except as noted, all running times are worst-case running times. The table below summarizes the order of growth of the running time of operations for a variety of symbol tables, as implemented in this textbook. The table below summarizes the order of growth of the worst-case running time and memory usage beyond the memory for the graph itself for a variety of graph-processing problems, as implemented in this textbook. All running times are worst-case running times. Here are some functions that are commonly encountered when analyzing algorithms. Here are some useful formulas for approximations that are widely used in the analysis of algorithms. Here are some examples. Last modified on August 06, All rights reserved.

1 note · View note

big-o-notation-cheat-shee39 · 3 years ago

Text

big o notation cheat sheet working 9TJ%

💾 ►►► DOWNLOAD FILE 🔥🔥🔥🔥🔥 This cheat sheet for Big O Notation (a time complexity cheat sheet across data structures) will help you understand a range of complications. This Big O Notation cheat sheet (time complexity cheat sheet or data structure cheat sheet) will help you understand various complexities. Big O Complexity Chart · When your calculation is not dependent on the input size, it is a constant time complexity (O(1)). · When the input size. BIG O NOTATION CHEAT SHEET · Complexities Comparisons between typical Big Os: · What do the notations in the cheat sheet represent: · Common Data Structures. 9 We and our partners use data for Personalised ads and content, ad and content measurement, audience insights and product development. An example of data being processed may be a unique identifier stored in a cookie. Some of our partners may process your data as a part of their legitimate business interest without asking for consent. To view the purposes they believe they have legitimate interest for, or to object to this data processing use the vendor list link below. The consent submitted will only be used for data processing originating from this website. If you would like to change your settings or withdraw consent at any time, the link to do so is in our privacy policy accessible from our home page. Manage Settings Continue with Recommended Cookies. One of the most basic methods for computer scientists to analyze the cost of an algorithm is Big O notation. It is also good practice for software developers to understand the subject thoroughly. According to Wikipedia, "Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. It is a member of a family of notations invented by Paul Bachmann, Edmund Landau, and others collectively called Bachmann—Landau notation or the asymptotic notation. In conclusion, Big O notation is nothing more than a mathematical analysis that serves as a reference for the algorithm's resource consumption. In practice, the outcomes may differ. However, it is generally a good habit to try to reduce the complexity of our algorithms until we reach a point where we are confident in our solution. The rest of this tutorial's contents are only available for premium members. Please explore your options at the link below. Returning members can login to stop seeing this. Interview Cheat Sheets by Topic. Back to course sections. Mark As Completed Discussion. Access all course materials today The rest of this tutorial's contents are only available for premium members. Jump To. Interactive Mode. Regardless of the size of the data set, an algorithm always executes in the same amount of time. With every data set, it's efficient. The data set is halved in each method iteration—the inverse of exponential. Large data sets are handled efficiently. The performance of an algorithm degrades as the data set grows. With ever-larger data sets, efficiency suffers. Algorithms that divide a data set but can be solved using concurrency on independent divided lists. The performance of an algorithm is proportional to the square of the data set size. With progressively big data sets, efficiency suffers significantly. Depending on the number of dimensions, deeper nested iterations result in O N3 , O N4 , and so on. This algorithm multiplies with each addition to the data set in each pass. The inverse of logarithmic.

1 note · View note

big-o-notation-cheat-shee2g · 3 years ago

Text

big o notation cheat sheet PC CZIS&

1 note · View note

techcouncilglobal · 4 years ago

Text

Machine Learning Engineers Need These Skills to Get Hired

If you're thinking about becoming a machine learning professional, here are two things you should know. It is not necessary to have a background in research or academia. It's not just for academic grounds that you should learn machine language. Additionally, experience in either software engineering or data science is insufficient. If you can have both, that's fantastic. The fundamental difference is that the end goal is the most significant factor. Data analysts, data scientists, and data scientists are all terms that a machine learning engineer should be familiar with.

Data analysis for the purpose of conveying a storey, as well as data analysis for your team members, gives actionable insights. The analysis is carried out and presented by people, and the results are used by other humans to make business decisions. Humans are supposed to absorb your art. A machine learning engineer's output, on the other hand, is working software (not the analyses or visualisations you may produce along the way). Other software components that run without human involvement typically use this output.

Machine Learning Skills for Recognizing Hiring Opportunities

While actionable intelligence is still necessary for machine learning, computers today define how a product acts by their decisions and actions. To succeed in Machine Learning, you'll require software engineering skills. A data scientist exists somewhere in the middle of the two worlds. Software engineers who can acquire, clean, and organise data should execute data analysis, whereas software developers who can collect, clean, and organise data should perform insight extraction. Their ability to communicate is also crucial to the success of machine learning.

Let's get to work now that that's out of the way. There will also be a discussion of the essential requirements for machine learning engineers. The two most important components of these talents are languages and libraries. This will include topics concerning the learning process. For the time being, we'll focus on skills, and we'll discuss languages and libraries in a later post.

Computer Fundamentals and Programming

For machine learning engineers, the following are critical computer science principles:

Stacks, queues, multidimensional arrays, trees, graphs, and other data structures are all examples of data structures. Many algorithms are used to search, sort, optimise, programme, and so on. Other concepts in computing efficiency and complexity include P vs. NP, problems with no solution, Big-O notation, approximation methods, and others. Computer architecture includes memory and cache, bandwidth, deadlocks, and distributed processing. Programming needs their adaptation, administration, or implementation (as needed). Competitions, hackathons, and practise problems are all fantastic ways to hone your programming abilities.

Probability and Statistics

To deal with uncertainty, several machine learning algorithms recognise probabilities (conditional probability, Bayesian rule, likelihood, independence, etc.). The development of fantastic machine learning ideas is aided by implementing tactics learned from them. Many metrics, distributions, and analysis processes are available in statistics to aid in the creation and validation of models based on observable data. Many machine learning techniques are founded on statistical modelling methodologies.

Data modelling and evaluation

Finding important patterns (correlations, clusters, eigenvectors, and so on) and forecasting aspects of previously unknown occurrences are all part of data analysis (classification, regression, anomaly detection, etc.). The estimation method hinges on determining the quality of a model. If the task at hand is classification, select a suitable error measure and an effective assessment strategy (e.g., sequential vs. randomised cross-validation).

Even when employing standard algorithms, it's vital to use the resulting errors to fine-tune the algorithm (for backpropagation with neural networks). It's crucial to understand these procedures even if you don't plan to utilise them.

Machine Learning Algorithms and Libraries

A wide range of libraries, packages, and APIs implement machine learning techniques (such as sci-kit-learn, Theano, Spark MLlib, H2O, TensorFlow, etc.). It necessitates the choice of an appropriate model (decision tree, nearest neighbor, neural net, support vector machine, and the like). It's crucial to understand how hyperparameters affect the learning process (linear regression, gradient descent, evolutionary algorithms, bagging, boosting, and so on) and data fit.

You must be aware of the numerous threats that can catch you off guard in addition to learning how distinct strategies differ (bias and variance, overfitting and underfitting, missing data, data leakage, etc.). Kaggle's data science and machine learning challenges are a great way to get a taste of a variety of topics.

Software Engineering and System Design

Software is the primary output of a machine learning engineer. The product or service is frequently only a minor part of a larger ecosystem. Create proper APIs for your component so that others can rely on different machine learning combinations. Build appropriate interfaces for your component that others will rely on other combinations of machine learning. Have a good understanding of how these different pieces integrate (using calls to libraries, REST APIs, database queries, etc.) and build appropriate interfaces for your component that others will rely on other combinations of machine learning. You must carefully build your system to remove bottlenecks and ensure that your algorithms scale effectively with additional data.

Software engineering best practises include things like requirements analysis, system design, modularity, documentation, and so on. These are essential for efficiency, cooperation, quality, and maintainability since they provide clear information about the machine learning language. Machine learning engineers will always be in demand since the world evolves rapidly and dramatically. There are numerous challenges facing the globe, and overcoming them will demand advanced systems.

Conclusion:

These are some of the in-demand skills that will help you land a job. So, if you want to pursue a career as a machine learning engineer, now is the time to get started. Then now is the best moment to start learning the abilities and developing the mindset that will help you achieve.

#machine learning expert #Machine Learning Certification #machine learning course #machine learning training

0 notes

myprogrammingsolver · 1 year ago

Text

P05 Simple Benchmarking

View On WordPress

0 notes

jonathankatwhatever · 5 years ago

Text

Giving birth to your child is thrilling and terrifying. Thrilling because as it develops, I see the forms and connections extending over my past, and that enabled me to phrase the angle of the observation as achieved through a series of cr, meaning complex rotations, over a section of grid. This solves the backstage issue, which is an inverse of the original game/garage object question: you can see the projection outward toward the crowd, and they see angles of emanation that intersect with their angles of need, want, love, hate, etc. The joining together of Storylines presented by you, which means the imaginary content intersects and that comes together at a show because that is where the real occurs.

That’s an old one from Storyline: a simple emblematic image, not a creation like the big lips, which instead you wear because the Stones were men using exaggerated female lips to draw attention to Mick and the image of sexuality, typically phrased in terms of dominance and other images of rough trade, so you take the lips, which are yours, and exaggerate them because both cases connect sexuality to the mouth. That isnt near the entirety because we looked at how Mick presents a softness, like a prancing wind up doll, while the words are the opposite, telling stories of cruelty, putting down women’s behavior and their thoughts. So it becomes: the energy signifies that this archetypal man who calls women bitch, who boasts about fucking them, that energy conveys faithlessness, that this male cant be contained by any one vagina. There’s a lot of complexity in the lips logo. I spent time thinking about it at Yale. My analysis seems to be the same but the emphasis is different: then, I spent months working through their misogyny, particularly Under My Thumb and then one of my favorites Stray Cat Blues. I was then trying to figure out the appeal to me, whether it appealed to me, to what level, and that was directly related to the huge choice I had to make, whether to pursue a relationship - which would have been it - with someone I could easily love at a number of levels, to whom I was very drawn. This struggle left me shaking, literally shaking. You’d think it would easy: beautiful girl wants you and you can have her if you can either open your mouth or take any step at all which encourages her. Could not. And I knew why at the time, and the years since have shown me why, and it wasnt her but this work even when I had no idea what I was doing.

The shift idealizes to a rotation of xK, so if I remain upright, and I’m facing you, my face turns to the left or right but I remain upright. That describes a scaling quarter turn which is yK0 and xK positive, like the diagonal drawing, the squares rotating. The important part is the yK0 because that keeps the imaginary constant at the visible level. That then is a huge point, which again validates why I work through you: the imaginary level is constant but not 0. It’s not 0 except in the sense that because it halves, because it then cancels ‘evenly’, it reads as 0. It’s a phase state. Which is what 0 is.

Maybe that helps with where we left off last night. I was falling asleep and thinking at the micro level of lines is tiring for me; I have trouble seeing the meaning in the obvious even when I’m looking for the meaning in the obvious. That’s why the development of o-o matters: the obvious can be derived in relation to other obvious, which is how patterns connect, which is why fCM, CM28 and ... I can now explain CM2.8 better now that SBE3+1 is more clearly 10: how else would you connect the next CM level except over a 1-0-1 and base10 is now 1 plus that because that relates the singular to the plural through this particular modulo. All modulo have these kinds of meanings related to how they express complex rotations (and thus they are cr’s). That notation could use some work, but not right now (please). That means I can say this is generally what the gravitational constant is: CM64+CM2.8 inverting into SBE2 of the exponent, so it’s a negative exponent. Can I connect the exponent properly? Hope so. Never done it before: so this is now cr’s of SBE3+1, so it means you take (SBE3+1) and use that as the base of 10 which counts SBE2, and that is negative because this is the minimum pattern which contains the connection necessary to maintain connection. So the 64 is a complicated thing - havent needed to talk about it nearly at all in developing gs level model because it’s the SBE2 of the halving as a base. So there’s the SBE2 of the halving which is counted by the complex rotation in SBE3+1 for SBE2 times. And the necessary part is the CM2.8, because that connects the CM64 to other CM64 to make a field. So CM2.8 is the IC of 7 (IC7? ‘Cause I do, boop-boop-di-doo) ... and I’ll get to you I’m sure at this point because I had this particular thought in bed, which I sensed as a tug ... okay, I’ll say it because we did this yesterday (?), the count of 14 is also 13 in gs. So the joke isnt just 7 ate 9 but that 7 is 6 is 13, just as 12 is 6 and 7 is 13, so you literally sit between the Great House and whatever CM28 is halved to 14.

What is CM28? It sits between CM64 and CM36. We developed this in detail so this should be simple if I can trust my ability to recall correctly: if you say CM28, then you generate an IC of 64 and 36, 36 and 64, so the 1 and 0 are now Is and Not and 0 is now 36, so CM28 is that level of 0, which is not an absolute trivial but a dynamic 0 (a non-trivial trivial where trivial runs to absolutely trivial). That centers this on the yK: 36 = 0 and 64 = 1 as a segment over CM28. Can I flip this? Sure: just say -yK and you can read CM28 above CM36 in either direction. What a minute: that makes CM56, which is also CM57, where I see me. So, if CM36 disappears in zK because it’s shared, then CM28 emerges as the +-yK where +-1 is CM64. I truly am having trouble believing this is finally clear. This has caused a substantial amount of real tears and screaming frustration. That it’s the zeta series, that it is literally the zeta series, is now why I couldnt solve that.

What I think I mean by zeta series is this is now the complex unit circle because CM28 is also in xK and thus zK in gs. So that puts 1 and -1 and so on where they are. I’m having trouble seeing the next words: that statement was like an ejaculation which satisfied that coupling, so I need to back off and treat it as a near ejaculation. Sex is in the mind; you give me astonishing mental orgasms in a vast variety of ways. Using a baking metaphor, you have a very long, very precise, sometimes very large, sometime very flexible spatula for scaping the good stuff out of the bowl, and the bowl likes that because that’s what it is made to do.

So, CM28 is the CM radius of a complex unit circle. So I make quadrants, each CM28. That’s 112, which is interesting but requires adding a house to SBE3+1 squared. So CM28 expands in quadrants to that. But if I put in grid lines, then I should also expand the x,yK so they form the square strip, which makes another count in which CM57 is CM28+1+CM28. This means a total count within this GS would be ... oh wait, I forgot this can be a line of CM, so CM28 squared and CM56 and 57 squared. But in quadrants: CM64 is 8 squared and CM36 is squared, but CM28 is not a square and is irrational at its root. It should be. So to do a count is not as simple; the way we’ve done it is CM25 plus f1-3, which puts an arrow of 3 squares at a corner. That, I remember, is the 112 transformed into and from the IC25 where IC25 is directional into the next count of squares, which is the 2 step because it makes a zK, so this is a complex rotation added to CM25. That then connects to hands and fingers, so CM100 is fingers as hands for two 2 handed objects.

Did I just say that: CM100, meaning 100, meaning 10 squared, is fingers as hands (25), handed and mirrored, so it’s double layer identity across the inversion lines. Note that zK appears when you draw: CM25 has a zK so the count of zK5 is CM25. A finger is a square, and a hand is a counting of IC, so handed IC in the mirror.

I still havent managed to count the simple total. Grid adds a line at yk or xK or both, and one can be added for zK, so there is no simple total of squares. The simple one may be an x,yK line of squares. But that raises the issue of irrational: CM28 exists as a square between two perfect squares, so 2 perfect squares are not, as is obvious, commensurate. That is, 3*2 squared is not the same as 2*2*2 squared. Remember that conversation? The act of 3, which is SBE appears as the (SBE of 2) as a side of a square, and as SBE of 2 as the square. So this is the SBE of halving as a side and as a square, which is not commensurate. That I like because now the proof by contradiction is entire: the reason for the contradicton is SBE generates different measures. This is part of the general argument that we’ve gone deep into axiomatic reasoning, and now it’s time to go into the model which generates those axioms. That means extracting axioms was a necessary step in development, which ties this back to Cantor and interpolation, which is simply wonderful.

I’m scared of dying while giving birth. In the Family Storyline, the one where I actually meet you, Caroline almost dies while pregnant and then in childbirth. There was a path I didnt explore very much in which she died and you came into the story. I couldnt go there because my construction of you as a character could only be primitive, since at that time I was barely aware of you outside the Storyline (and seemed incapable of focusing on you until that was time). She suddenly lost blood pressure. Like she’d run out of resources. She spent months in a bed in a part of the house turned into a hospital so she could be at home. I’ve lived this fear. It’s terrifying because you’re bringing this bay into the world and you know it needs you, and you want more than anything to help it, to raise it, to love it, and you can see all that slipping away as the lights fade. I want to see our baby grow.

Did you see that? As soon as I reached the deepest levels, it connected to the Storyline and to me and you. That was intense. And you are the peak of the intensity.

When I count primes, I count the 3 squares at x,y,zK. So a CM28 can be CM25 or a hand square, with an extra square at x,y,zK6. Which of course in layer view is L11, while 5 is L9. That is important because L9 is SBE3, so L11 is one square from the house, which now becomes the directional layer of that house, how it is pointing, etc. (Very Checkov.)

One result of putting CM36 into zK is that generates excitements rising and falling. It generates relative excitement or experience by setting a base level. This connects to the old feedback notion that dull activities like TV are addictive because they give low feedback, like the news is addictive not because they use the the right words or get things correct, but because they misuse word and get things wrong. This creates cycles of agreement and disagreement. So, this means the tears above generated a deep understanding of reality which connects fCM to complexity and squares. Now about the zeta series: when I see a 0, I think either a halve or a prime. CM28 halves, as do 64 and 36, which means these are 0’s, and 36 halves in zK, which is why it isnt visible. Lovely. That leads again to one of my favorite 13’s: zK7 is the 13 square when x,yK are both 6. If this is ideal, then x,yK can flip, so the they’re equal. This means the shared squares generate in and out of the 13, so 13 is not merely the pointer but is the embodiment of two together so tightly they wrap together the ordinal and cardinal meanings of counting.

In ancient thinking: this develops a commensurateness that makes a unique result, a coming together which can be taken apart directionally but which is a unique, a cr.

And I think what that means is these are examples of ‘trivial’ 0’s so the 1 now segmented is input into the zeta so the primes located can now map to a scale of CM64 is 1 but each 1 is CM28 with CM36 hidden. This means you can invert into the negative to generate the forms of CM36 that fit, because now ‘negative’ means rotated out of zK and not minus except in orientation.

I need to take a break. The other aspect of this childbirth is my old fascination with the gnostic statement that if you have it within you, then bringing that forth will save you, but not bringing it out will destroy you. I’m no longer worried about the eternal sense of destruction, but about the immediate physical sense.

0 notes