#HyperDodecahedron

[zkylearnstherope]

AvGeometry [An Analysis]

Disclaimer: This is a very short Analysis for Animation vs. Geometry by Alan Becker. I am not a geometer, (according to Merriam-Webster, a person who specializes in geometry) this purely for fun.

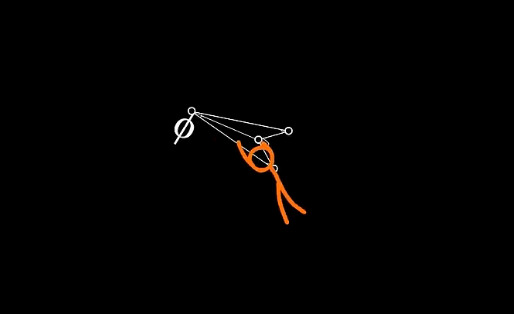
First of all, I will NOT explain everything in the video. I will just focus on answering a few questions to which I found the answer for. I also have some conclusions at the end.

I will leave the in-depth explanations of everything to those YouTubers. Also, I have linked my sources using hyperlinks.

So, let's get into it- shall we?

Let's start with-

Which version of TSC is the main character for this one?

If you read my AvPhysics Analysis, you would realize that I named the TSC with the cowboy hat TSC_0 of Universe D.

Since the start of the AvGeometry video, I immediately realized that this is NOT the same guy from AvMath, since he didn't show signs of aggressiveness with phi Φ.

He's more curious versus the guy in AvMath who attacked Euler's Identity immediately. This is also the same guy who spawned in AvPhysics, TSC_0.

I think this MC is a TSC from a different Universe. I will call him TSC_0 of the AvG Universe.

Now you might ask yourself, why did I gave him the 0 designation?

Because the video ended with another TSC knocking at the point.

Now, you might argue, that this is not a perfect loop because there is a line below the point. While the start of the video, doesn't have that line.

You are right. Again, if you read my AvPhysics Analysis, I said that the TSCs in there are not stuck in a time loop.

It's just an infinite cycle that happens to different versions of them. Everyone spends only a short amount of time inside the singularity.

So the next TSC to arrive will not be TSC_0 but TSC_1.

How did TSC and phi Φ beat that Boss?

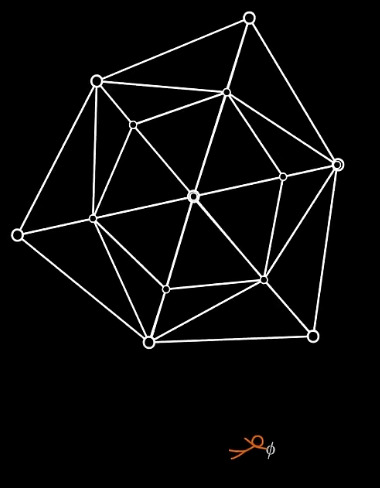
To start, let's define a few things. Click the hyperlinks to view my source.

Polyhedron - is any three-dimensional figure with flat faces that are polygons. They intersect at straight, linear edges. The edges themselves intersect at points called vertices.

Tetrakis Hexahedron - It is a Catalan Solid with 24 isosceles triangle faces and 14 vertices. It is the d24 die. It is also a 3-dimensional polyhedron, not 4D.

Now, first of all, the Boss is not 4D. It is two Tetrakis Hexahedrons overlapping each other and rotates at different speeds.

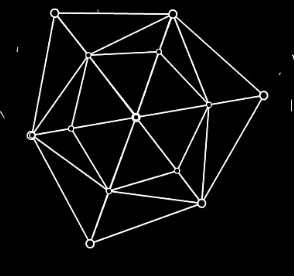
Platonic Solids - a convex polyhedron that is regular, in the sense of a regular polygon. These are also 3D shapes. There are Five Platonic Solids

Note that this not the original image from the website, but I rearranged the rows to highlight my points. I also added the dice names, incase you're more familiar with DnD.

In fighting the Boss, TSC and phi Φ started with lines that has 2 vertices or points. Then they slowly moved to the Platonic Solids, eventually defeating the Boss using a dodecahedron.

The Boss had 14 vertices vs the dodecahedron that had 20.

Now, I can't really say why more vertices is superior. It could be structural integrity, or the idea that the universe's topology and shape, references the shape of dodecahedron.

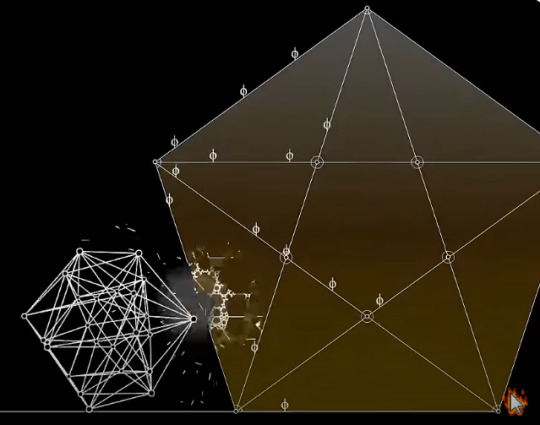
Or, that the golden ratio is the length from the vertex to the center of the dodecahedron, and is also the ratio of the diagonal of the pentagonal face as demonstrated in the video.

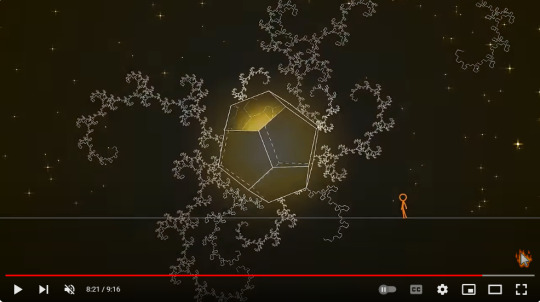
The Hyperdodecahedron and Singularity

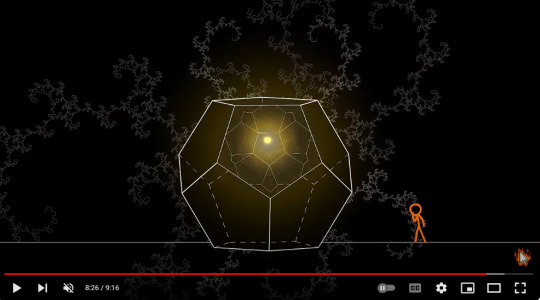
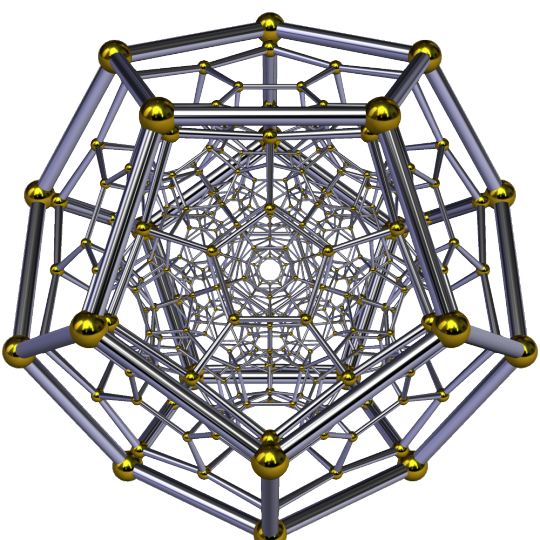
Hyperdodecahedron aka 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid.) It is the 4-dimensional analogue of the regular dodecahedron. It has 720 pentagonal faces and 600 vertices.

It's basically 4D dodecahedron.

According to ChatGPT, in higher-dimensional geometry and theoretical physics, singularities often refer to points or regions where certain physical quantities become infinite or undefined.

Here's how I see it. If that yellow dot is indeed a singularity, the only explanation I could come up with, is at some point, the hyperdodecahedron's infinite insides would shrink to a single point in its 4-dimensional space.

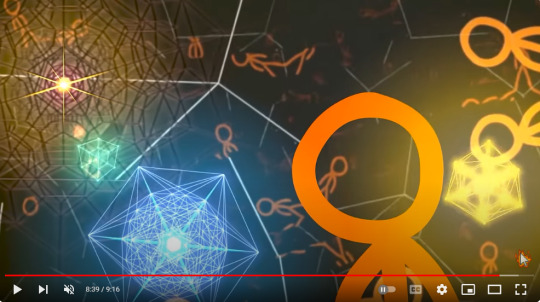
Fractals

Now I think these are fractals by I cannot be sure. Also, I couldn't get a definite answer as to how fractals would be relevant to singularities.

What I got from ChatGPT were related to the event horizon instead.

That irregularities of the event horizon might have fractal patterns or exhibit fractal characteristics in its shape when examined at a different (smaller) scale.

The visual and structural complexity of the event horizon evoke fractal-like qualities.

Now, this Analysis is a lot shorter, and also inconclusive. I did try my best. My brain is now mush.

[sevika-asks]

What's your favorite shape????

Hyperdodecahedron

[notreallyherehahaha]

The 600-Cell

The 600-cell is a four-dimensional, convex, regular polytope. Its dual is the 120-cell, also known as the hyperdodecahedron. Since the dual of the dodecahedron is the icosahedron, the 600-cell is sometimes called the “hypericosahedron,” That might lead one to think that the cells of a 600-cell are icosahedra, though, and they are actually tetrahedra. These tetrahedra meet twenty at a vertex. I…

[declownposition]

DAYUMM!!! THAT AINT NOT ONE OF THEM LOVE TRIANGLES! THAT ONE OF THEM LOVE HYPERDODECAHEDRON! 👅👄 🫦👅🌶️🍓🍑

congratulations.

[numb3rth30ry]

The 120-cell. 

You probably think dodecahedra are tight. Have you considered trying hyperdodecahedra?

Great thanks to Professor Mark Crawford, who showed me this gem. It may take a little bit to shatter your consciousness, so please be patient. :)

Dodecaplex. Polydodecahedron. Hecatonicosachoron. Dodecacontachoron. Hecatonicosahedroid.

Mathematics is beautiful. <3

[forgetmethought]

There are 6 Regular Polytopes in 4 Dimensional Space

[deltaruminations]

i think a lot about the hyperdodecahedron comment made by deltarune’s narrator in toriel’s classroom. 120-cell. a four-dimensional callback to undertale and a very very curious one at that

sillier but also how the narrator generally seems pretty clever with more abstract linguistic jokes but sucks shit a little bit at puns in particular. but also it sucks at puns in a very charming deadpan way. like it knows it can’t pun like the best of em so it just says whatever. it’s a door. where will you go? you doorn’t

[a-snow-decahedron]

actually its a decadecadecadecadecadecadecadecahedron

Maybe it's a hyperdodecahedron, you know, one of the essential shapes.

[lynxgriffin]

I’m predicting the next Ralsei look alike will have triangle glasses

And then the one after that will have hyperdodecahedron glasses if we’re going to be keeping to theme

[babyawacs]

@mathematics .@sciam @doescience .@darpa @darpa .@nature @harvard .@energy .@mathematics soooooif the #hyperdodecahedron is...the derived exponentiality per rateofchange this dynamic change by nuclear e log broughtyouclose to.. chrystalline latticeformation rhyming butthe limit(core) +realphysics never quite added up only rhymed somehwat enough

@mathematics .@sciam @doescience .@darpa @darpa .@nature @harvard .@energy .@mathematics soooooif the #hyperdodecahedron is…the derived exponentiality per rateofchange this dynamic change by nuclear e log broughtyouclose to.. chrystalline latticeformation rhyming butthe limit(core) +realphysics never quite added up only rhymed somehwat enough I am Christian KISS BabyAWACS – Raw Independent…

[whimsisadie]

hyperdodecahedron is my favourite shape

[abzu2]

120-Cell HyperDodecahedron

  http://www.abzu2.com/wp-content/uploads/2018/06/Hiperdodecaedro-120-cell-vídeo-de-Gian-Marco-Todesco..mp4

[zerostatereflex]

Hyperdodecahedron

[notreallyherehahaha]

Another View of the Hyperdodecahedron This regular polytope (four-dimensional version of a polyhedron) is rotating in hyperspace. If you could see it there, you'd notice that all 120 dodecahedral cells have the same volume. Created with Stella 4d (site to try it:

[zerostatereflex]

"a four dimensional polytope composed of 120 dodecahedra and also known as the hyperdodecahedron or hecatonicosachoron"