#NumberTheory

[rbrooksdesign]

"DMT_106," digital + acrylic, July 16, 2024, Reginald Brooks

DMT = Divisor (Factor) Matrix Table

[klikomo]

#interestingfacts 90

Follow for what’s trending and interesting around the world 🌍

[tmarshconnors]

"A fool is known by his speech, and a wise man by silence."

Pythagoras, a Greek mathematician and philosopher, lived around 570-495 BCE. While much of his life is shrouded in mystery and legend, here are five lesser-known or potentially rare facts about Pythagoras:

Secretive Cult-Like Community: Pythagoras founded a secretive and exclusive community in Croton, Italy, known as the Pythagorean Brotherhood. The members of this community were bound by strict rules, including a vow of silence and a communal way of life. The group was not only interested in mathematics but also philosophy, mysticism, and religious practices.

Numerical Mysticism: Pythagoras and his followers believed in the mystical significance of numbers. They thought that numbers held inherent qualities and mystical properties. For example, they associated odd numbers with masculinity and even numbers with femininity. The number 10 was particularly significant and seen as a perfect and divine number.

Pythagorean Theorem was known before Pythagoras: While Pythagoras is credited with the famous Pythagorean Theorem, which relates the lengths of the sides of a right-angled triangle, evidence suggests that the theorem was known to the Babylonians and Indians before Pythagoras. Pythagoras, however, is often credited with its formal proof and popularization in ancient Greece.

Vegetarianism and Taboos: Pythagoras and his followers were known for their strict dietary restrictions. They practiced vegetarianism, believing that it was essential for purifying the soul. They also had various food-related taboos, such as avoiding beans, possibly due to their belief in the impurity associated with certain legumes.

Pythagorean Cup: Pythagoras is associated with the invention of the Pythagorean cup, also known as a "greedy cup" or "tantalus cup." It's a clever drinking vessel with a hidden mechanism that causes the cup to drain its contents if filled beyond a certain level. This invention is often attributed to Pythagoras as a symbolic lesson in moderation and self-control.

[pkmathyt]

Math Olympiad Problem, This Question Surprised Many People

[edgythoughts]

Why Are Prime Numbers Important 2025

Why Are Prime Numbers Important 2025

The Book-Style Answer (What Teachers Want You to Know) Prime numbers are the building blocks of all other whole numbers. A prime number is any number greater than 1 that has exactly two distinct positive divisors: 1 and itself. This means it can’t be divided evenly by any other whole number. Some common examples: 2, 3, 5, 7, 11, 13, 17… Why do they matter so much? 1. They’re the foundation of number theory. Every whole number greater than 1 can be written as a product of prime numbers — this is called the Fundamental Theorem of Arithmetic. So just like atoms build up all matter, prime numbers build up all whole numbers. 2. They keep your data safe. Prime numbers are the unsung heroes of modern encryption. Most security systems — from online banking to private messaging — rely on the difficulty of factoring very large prime numbers. It’s super easy to multiply two big primes together, but ridiculously hard (even for computers) to reverse-engineer the original primes from their product. 3. They help us understand math patterns. From geometry to algebra to complex algorithms, prime numbers often pop up in surprising places — especially when we try to find patterns or predict outcomes in large sets of numbers. 4. They’re deeply mysterious. We’ve been studying primes for over 2,000 years, and there’s still no formula that generates all of them. We don’t even know if there's a pattern to their distribution. Mathematicians are still chasing answers. In short, prime numbers might look random, but they’re a kind of mathematical gold: rare, powerful, and fundamental. —

The Real-Talk, Friendly Version Alright, let’s be honest. When you first hear the phrase "prime numbers," you probably feel your brain start to glaze over. Like — why do we care if 7 can’t be divided by anything but 1 and itself? That’s not exactly Netflix material. But here’s the truth: prime numbers are the rebels of the math world. They don’t follow the crowd. They can’t be split evenly by anyone except themselves and 1. They’re fiercely independent — and somehow, every single other number in existence is made from them. Seriously — all the big, complicated numbers out there? They’re just prime numbers multiplied together in different ways. So if math were made of LEGO bricks, prime numbers would be the tiny core blocks that everything else snaps onto. But that’s not even the coolest part. Prime numbers are also your digital bodyguards. You know how you can buy stuff online, text your friend something super personal, or check your bank account without everyone on the internet reading over your shoulder? That’s all thanks to prime numbers and encryption. The tech basically hides your info inside really big prime number puzzles that only your computer can solve. And get this — even though we’ve been studying them forever, we still don’t know why primes act the way they do. They’re unpredictable. Mysterious. Beautifully weird. Some of the smartest people alive are still trying to crack their secrets. So yeah — primes might seem like just a math thing, but they’re actually everywhere, from your phone security to ancient codes to theories about the universe. They matter. A lot. — External Resource: Want to dig deeper into the mystery of prime numbers? Check the Wikipedia page: Prime Number https://en.wikipedia.org/wiki/Prime_number — Related Articles from EdgyThoughts.com: Why Is Zero So Powerful in Math 2025 https://edgythoughts.com/why-is-zero-so-powerful-in-math-2025 Why Infinity Isn’t Just a Number 2025 https://edgythoughts.com/why-infinity-isnt-just-a-number-2025 — Disclaimer: The following easy answer is written in a simplified and relatable style to help you understand the topic better. If your teacher expects the textbook version and you write this instead, we are not responsible for any loss of marks. Our goal is purely to make concepts easier to grasp. — Read the full article

[custodiomxx]

[speedywonderlandtrash]

Numbers in Everyday Life: Understanding Their Importance

Numbers in Everyday Life: Understanding Their Importance

Numbers in Everyday Life: Understanding Their Importance is a document that delves into the significance of numbers in our daily lives. It emphasizes the importance of understanding and valuing numerical concepts. A Deep Dive into the Types, History, and Role of Numbers in Modern Life The Story of Numbers: An Integral Part of Human Life   Numbers are more than just tools for calculation; they are interwoven into every aspect of human life. From the earliest lessons of counting natural numbers to the more advanced use of complex numbers, we have relied on numbers to describe, measure, and make sense of our world. Numbers, in their various forms—whole numbers, integers, rational numbers, irrational numbers, and even imaginary numbers—are essential for understanding the universe. 1. What is a Number? A number is a concept that allows us to quantify objects, measure distances, and even solve complex problems. Whether we use natural numbers for simple counting or complex numbers for advanced equations, numbers help us structure the world. Numbers, in essence, are at the heart of mathematics and number theory, the study of the properties and relationships of numbers. 2. Natural Numbers: The Foundation Natural numbers are the most basic numbers we use to count: 1, 2, 3, and so on. They are part of what is known as the set of real numbers, which also includes integers, rational numbers, and irrational numbers. When a child begins counting toys, they are using natural numbers. However, the concept of zero, introduced later, expands natural numbers into whole numbers. 3. Whole Numbers: Including Zero Whole numbers are simply natural numbers plus zero. The inclusion of zero is crucial because it represents the absence of quantity. This small addition makes a big difference in counting systems, allowing for more advanced mathematical concepts. For example, in everyday life, we use whole numbers to represent both something (3 apples) and nothing (0 apples). 4. Integers: Going Beyond Positives Integers expand the world of numbers by including negative numbers. The set of integers consists of positive numbers, negative numbers, and zero. For example, -3, 0, and 5 are all integers. In practical situations, integers are useful for representing gains and losses, such as financial transactions. If you lose $10, that loss is represented by the integer -10. 5. Rational Numbers: The World of Fractions Rational numbers are those that can be expressed as a fraction of two integers. This includes whole numbers, but also numbers like 1/2, 3/4, or 7/8. In real life, rational numbers allow us to divide and measure in portions. For instance, if you eat half a pizza, you're using a rational number (1/2) to describe that portion. 6. Irrational Numbers: Infinite and Non-Repeating Some numbers, however, cannot be written as a simple fraction. These are called irrational numbers. Famous examples include √2 and π (pi). The number π is essential for calculations involving circles, and its value continues infinitely without repeating. These numbers arise naturally in many areas of geometry and calculus, revealing deeper truths about shapes and spaces. 7. Real Numbers: Rational and Irrational Together Real numbers encompass both rational and irrational numbers. They are the foundation of most mathematical operations in everyday life and science. Any number you can place on a number line is a real number, whether it's a whole number, fraction, or irrational number like π. Real numbers allow us to calculate, measure, and describe virtually everything in the physical world. 8. Complex Numbers: Beyond Reality Complex numbers take the concept of numbers even further by combining a real part and an imaginary part. A complex number is written as a + bi, where "a" is the real part and "bi" is the imaginary part. The imaginary number "i" is defined as the square root of -1. Although they may seem abstract, complex numbers have real applications in fields like electrical engineering and quantum physics. 9. Prime Numbers: Building Blocks of Integers Prime numbers are special natural numbers greater than 1 that can only be divided by 1 and themselves. For example, 2, 3, 5, and 7 are prime numbers. Prime numbers are fundamental in number theory because any integer can be expressed as a product of prime numbers, a concept known as prime factorization. This makes prime numbers the building blocks of all other numbers. 10. Even and Odd Numbers: A Simple Division Numbers are classified into even and odd categories based on their divisibility by 2. Even numbers, like 2, 4, 6, and 8, can be divided by 2 without a remainder. Odd numbers, like 1, 3, 5, and 7, leave a remainder of 1 when divided by 2. This simple classification is used in many real-world applications, from dividing objects equally to coding. 11. Ordinal and Cardinal Numbers: Position and Quantity Cardinal numbers are used to count objects, answering the question "How many?" For example, "There are 5 apples." Ordinal numbers, on the other hand, indicate the position of something in a list: "first," "second," "third," and so on. Cardinal numbers are crucial for understanding quantities, while ordinal numbers help in organizing and ranking. 12. The History of Numbers: From Ancient Times to Modern Day The concept of numbers has evolved over millennia. Ancient civilizations such as the Egyptians, Babylonians, and Greeks developed their own systems for counting and measurement. The decimal system (base 10) that we use today was developed in ancient India and later transmitted to Europe through the Arab world. Roman numerals, such as I, V, and X, were also widely used in ancient times and are still seen in specific contexts today. 13. The Importance of Numbers in Daily Life Numbers are essential to almost every part of our lives. Whether we’re measuring distances, calculating time, or making financial decisions, numbers are at the core of what we do. In modern technology, binary numbers (0 and 1) are used in coding and computing. From the prices we see at the store to the data we analyze in science and business, numbers help us quantify and make sense of the world. 14. The Role of Numbers in Mathematics and Science In mathematics, numbers form the foundation of number theory and various branches of mathematics. Calculations in physics, chemistry, and biology all rely on the use of numbers to describe the laws of nature. Prime numbers, irrational numbers, and complex numbers all play critical roles in these scientific fields, solving complex problems and helping advance human knowledge. Conclusion: The Beauty and Power of Numbers Numbers are more than symbols; they are tools that help us understand the world. Whether we are counting objects, measuring distances, solving equations, or describing the universe, numbers are indispensable. Their beauty lies in their simplicity and complexity. From basic counting to the infinite complexity of irrational and imaginary numbers, the world of numbers is vast and full of wonder. As we continue to explore and innovate, numbers will remain a guiding force in science, technology, and everyday life. Their significance cannot be overstated, as they form the very language of the universe. Read the full article

[frnwhcom]

David Hilbert’s 23 problems, presented in 1900, are a famous set of problems that have guided much of 20th-century mathematics. These problems were translated and published in the Bulletin of the American Mathematical Society in 1902. Here’s a brief overview of each:

[sifytech]

Mathematics – Basis of Everything, Everywhere in the Universe

The discovery of the connection between genetics and pure mathematics highlights again how the universe is more logical and pattern based than most realise writes Satyen K. Bordoloi. Read More. https://www.sify.com/science-tech/mathematics-basis-of-everything-everywhere-in-the-universe/

[dappersautismcreature]

yall im totally going down a rabbit hole (researching wayyy past what i need to for the 4maxhalo cowboy AU im planning) but qsmpblr... did yall know binary code has existed since like, the 1500's? not quite as a code, from what i can tell (help me im literally reading some musty old pdf from 1981) but for math, in fact there is speculation it may have existed earlier. (help me i am reading an old math website from 2006 that obviously hasnt graced a screen in over a decade -__-) basically i thiink it was is that in egypt they used a shorthand (instead of modern day calculators lmao) to multiply larger numbers, for example 60X70, by dividing one number by two a bunch of times and doubling the other number the same amount of times.

so binary in computers comes from halving, mathematical roots.

there is another instance of direct language to a sort of binary substitution cipher, but instead of 1's and 0's it is A's and B's and random instead of following a pattern. this was first seen in the 1600's.

then the modern day understanding of binary code to numbers started, in the 1920's and 30's with a number represented in 1's and 0's based on halving, like this:

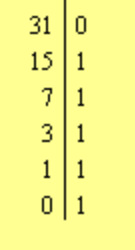
^^ if you look at this chart you'll see that they halve 125, but instead of using decimals, they have a remainder, and that remainder decides whether it is a 1 or a 0. isnt that interesting? this was being created in the early days of computing when basic calculations took a lot of design and thought.

so calculators, when doing big multiplications and such, will go through a series of simpler dividing and multiplying in twos, based off of the binary code assigned to the inputted factors.

like these examples

so unfortunately this means that in the wild west (im going for 1870's-90's) they sadly would not know what binary code is :((

still,, isnt this fascinating?? O____O

*holding gun up* isnnt is-isnt this fascinating O____O?

heres the sources btw: https://www.cs.cas.cz/portal/AlgoMath/NumberTheory/Arithmetics/NumeralSystems/PositionalNumeralSystems/BinarySystem.htm#:~:text=The%20modern%20binary%20number%20system,used%20symbols%200%20and%201.

[3] �Glaser, A. (1981). History of binary and other nondecimal numeration (Rev. ed.). Los Angeles: Tomash Publishers.

[rbrooksdesign]

"DMT_89," digital + acrylic, June 29, 2024, Reginald Brooks

DMT = Divisor (Factor) Matrix Table

[livesanskrit]

Send from Sansgreet Android App. Sanskrit greetings app from team @livesanskrit .

It's the first Android app for sending @sanskrit greetings. Download app from https://livesanskrit.com/sansgreet

Srinivasa Ramanujan.

Srinivasa Ramanujan FRS (22 December 1887 – 26 April 1920) was an Indian mathematician. Though he had almost no formal training in pure mathematics, he made substantial contributions to mathematical analysis, number theory, infinite series, and continued fractions, including solutions to mathematical problems then considered unsolvable.

#sansgreet #sanskritgreetings #greetingsinsanskrit #sanskritquotes #sanskritthoughts #emergingsanskrit #sanskrittrends #trendsinsanskrit #livesanskrit #sanskritlanguage #sanskritlove #sanskritdailyquotes #sanskritdailythoughts #sanskrit #resanskrit #celebratingsanskrit #sreenivasaramanujan #srinivasaramanujan #ramanujan #nationalmathematicsday #mathematician #mathematics #maths #mathematical #mathematicians #numbertheory #erode #indianmathematician #ramanujanmathpark #madrasuniversity

[weepingdreamerdefendor]

Celebrating National Mathematics Day: Honoring Srinivasa Ramanujan's Legacy

https://princesnowherashaikh.com/celebrating-national-mathematics-day-honoring-srinivasa-ramanujans-legacy/

December 22nd marks a special day in the world of mathematics - National Mathematics Day in India. This day commemorates the birth anniversary of one of the most brilliant mathematical minds in history, Srinivasa Ramanujan. As we celebrate this day, we not only honor Ramanujan's extraordinary contributions to mathematics but also reflect on the importance of mathematical education and innovation in our society. #nationalmathematicsday #srinivasaramanujan #mathgenius #indianmathematician #numbertheory #infinity #mathematicalanalysis #ghhardy #cambridgeuniversity #ramanujanprime #mockthetafunctions #drnowhera #heeragroup #matheducation #indianscience #mathematicalprodigy #december22 #mathhistory #numberpatterns #STEducation and Employment News 2.0

[pooja-987pooja]

Celebrating National Mathematics Day: Honoring Srinivasa Ramanujan's Legacy

https://princesnowherashaikh.com/celebrating-national-mathematics-day-honoring-srinivasa-ramanujans-legacy/

December 22nd marks a special day in the world of mathematics - National Mathematics Day in India. This day commemorates the birth anniversary of one of the most brilliant mathematical minds in history, Srinivasa Ramanujan. As we celebrate this day, we not only honor Ramanujan's extraordinary contributions to mathematics but also reflect on the importance of mathematical education and innovation in our society. #nationalmathematicsday #srinivasaramanujan #mathgenius #indianmathematician #numbertheory #infinity #mathematicalanalysis #ghhardy #cambridgeuniversity #ramanujanprime #mockthetafunctions #drnowhera #heeragroup #matheducation #indianscience #mathematicalprodigy #december22 #mathhistory #numberpatterns #STEducation and Employment News 2.0

[cleverenemyking]

Celebrating National Mathematics Day: Honoring Srinivasa Ramanujan's Legacy

https://princesnowherashaikh.com/celebrating-national-mathematics-day-honoring-srinivasa-ramanujans-legacy/

December 22nd marks a special day in the world of mathematics - National Mathematics Day in India. This day commemorates the birth anniversary of one of the most brilliant mathematical minds in history, Srinivasa Ramanujan. As we celebrate this day, we not only honor Ramanujan's extraordinary contributions to mathematics but also reflect on the importance of mathematical education and innovation in our society. #nationalmathematicsday #srinivasaramanujan #mathgenius #indianmathematician #numbertheory #infinity #mathematicalanalysis #ghhardy #cambridgeuniversity #ramanujanprime #mockthetafunctions #drnowhera #heeragroup #matheducation #indianscience #mathematicalprodigy #december22 #mathhistory #numberpatterns #stemintelugu

[fasalquran]

DECODE QURAN Digital Roots and Quantum Computing WILL SIMPLIFIEL THINGS

Discover the fascinating world where numbers and quantum physics intertwine in our latest video! 🌌✨ Uncover how digital roots simplify complex calculations and their surprising connection to quantum computing. Learn about the astonishing capabilities of qubits, existing in superposition and revolutionizing problem-solving speeds. Dive deep into the principles of error correction crucial for maintaining accuracy in both digital roots and quantum computing. See how these concepts share a common theme: reducing complexity to reveal hidden structures and patterns governing our universe. Prepare to be amazed at the convergence of number theory and quantum mechanics!

🔢 #DigitalRoots #QuantumComputing #MathMagic #PhysicsFun #Superposition #HiddenPatterns #NumberTheory #TechRevolution

If you enjoyed this video, don't forget to like and share!

OUTLINE:

00:00:00 simplified computing 02:11:36 The Magic of Digital Roots 02:12:30 A New Realm of Computation 02:14:11 Unexpected Cousins in Simplification 02:15:03 From Numbers to Qubits 02:16:00 Digital Roots and Quantum Speed-Ups 02:16:55 From Number Theory to Quantum Mechanics 02:19:01 Windows into Hidden Truths