#TheoryOfComputation

[asadmukhtarr]

"Introduction to the Theory of Computation" by Michael Sipser is a foundational textbook that explores the mathematical underpinnings of computer science. By reading this book, you will gain a deep understanding of computation, its limits, and its capabilities. Below is a step-by-step breakdown of the outcomes you can expect from studying this book:

[go-classes]

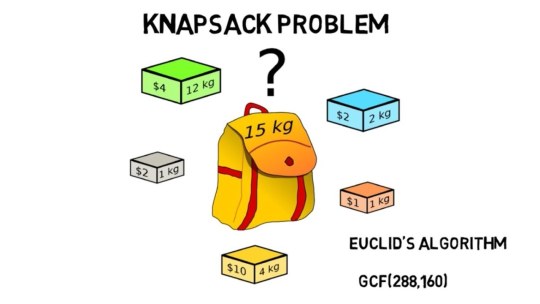
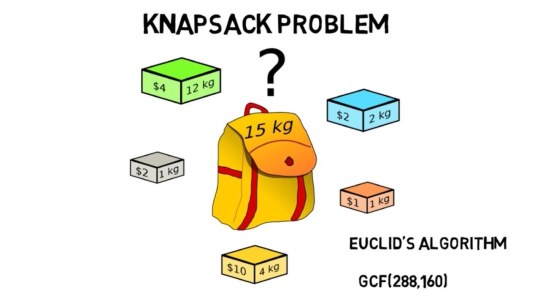
Wish to "Understand" All concepts of Theory of Computation... without By-hearting?? From Finite Automata to Decidability.. ▪️Understand concepts; don't rote-learn them.. GO Classes TOC Course: https://www.goclasses.in/s/store/courses/description/Theory-of-Computation-2023 GO Classes #GateCSE Complete Course: https://www.goclasses.in/s/pages/gatecompletecourse @goclasses_cse #GATECS #gate2023 #gate2022 #gateexam #gate #toc #automatatheory #theoryofcomputation #goclasses #gateexam #computerscience #goclassesmemes #gate2024 #gatecsit https://www.instagram.com/p/CjPtubZLgeH/?igshid=NGJjMDIxMWI=

[smartcherryposts]

NFA To DFA Conversion In Theory Of Computation

NFA To DFA Conversion In Theory Of Computation Construct The DFA For The Following NFA

    DFA Using DFA Transition Table If All States Are Final The Minimal DFA Will Be

My Initial State Will Be My Final State And This Is The DFA.   Example-2

Conversion Of NFA To DFA

Find The Minimal No Of States In NFA

Solution:- Transition Table For Given Diagram

This Is One Of The Different Questions. To Solve This Question We Are Going To Use Short Cut. If You Are Expert In Constructing DFA, You Can Solve This Question Using Short Cut.   The Question Given Is "Find The Minimal No.Of States In NFA" Means We Have To Find The Minimum No Of States In Given NFA.   There Will Be No Uniqueness In NFA. If It Is Not Unique, How Can We Find Minimal States?  

Remember

If The Question Is Asked To Find Minimal No Of States, The Diagram Should Be Unique And Should Be Minimal(Optimized) We Know DFA Means Minimized, We Can Construct Unique DFA, We Can Construct A Unique DFA For A Language. It Means The No Of States In DFA wILL Be Unique.   "Every DFA Is Not NFA" We Know But Every NFA Is Not DFA   Simple We Have To Draw DFA For Given NFA We Already Drawn Many DFA From NFA's In Previous Topics.   We All Know That Procedure.   But Here To Solve This Problem Using Short Cut. If We Can Predict The Language For Given NFA, Then We Can Find DFA Easily   I Have Solved Many Problems Before In Previous Posts We Have Seen How To Construct DFA Directly In Previous Solved Problems.   I Want You To Identify The Language For The Given Nfa & For That NFA For That Language, You Have To Draw DFA. Very SImple.

If You Observe Above NFA 0,1 Is Going To q0 Then After 3 Zero's 000, It Is Going To Final State. Means String Should ContainThree Zero's(000) Continuously For Sure And Final State q3 Has Loop Of '0', It Means The String Should End With Three Zero's(000) String Compulsorily Should Contain 3 Zero's This Is The Language For This Given NFA.   DFA

  Explanation For DFA

If I Get '1' , I'll Be On q0 Only If I Get '0 On 'q0' I'll Go To 'q1' If I Get '0' On 'q1' I'll Go To 'q2' If I Get '0' On 'q2' I'll Go To 'q3'(FINAL STATE) Because I Should Reach Final State Once I Get 3 Zero's String If I '1' On 'q1','q2','q3' I'll Go To Initial State 'q0' And I'll Start Machine Again I Cant Go To Dead State If I Get '1' On q1,q2,q3 If I Go To Dead State I Can't Get Back And I Cant Start The Machine Again   Read the full article

[btech-buddy]

Theory of computation

#theoryofcomputation

#automata theory

#computer science

[elle-baka-saru]

Quando vuoi #prendereilsole ma hai gli #esami a #settembre 😂 #legs #hotdogs #tanning #calcolabilitaecomplessita #automi #theoryofcomputation #lodoasettembre #potd #studying (presso Sarteano)

[alexminhtran4]

What is Computer Science? (Part 2: Algorithms, Computation, and more) Support the Channel: PayPal(one time ... #blogema #algorithms #computation #computerscience #computerscienceapplications #computersciencecourses #computersciencemajor #computerscienceprogramming #csc #cscmajor #majorincomputerscience #majorprep #majorprep #programming #theoryofcomputation #whatiscomputerscience

[alexminhtran2]

What is Computer Science? (Part 2: Algorithms, Computation, and more) Support the Channel: PayPal(one time ... #cyrrion #algorithms #computation #computerscience #computerscienceapplications #computersciencecourses #computersciencemajor #computerscienceprogramming #csc #cscmajor #majorincomputerscience #majorprep #majorprep #programming #theoryofcomputation #whatiscomputerscience https://cyrrion.com/what-is-computer-science-part-2-algorithms-computation-and-more/?feed_id=4985&_unique_id=5f28b422c38aa

[muzikaralar]

Liked on YouTube: Solutions for EVERY GATE Theory of Computation Question! [Exam Question Monday] #gateconcept https://www.youtube.com/watch?v=g_ZdcHSFGv0 In which we solve EVERY exam problem offered from GATE theory exams until 2020. There are 247 questions in this list, and we tackle (most of) them, and try not to lose our minds! Thank you all for supporting this channel - hopefully this is a good Memorial Day's viewing. #easytheory #nfa #dfa #gate #gateconcept #theoryofcomputing #turingmachine #nfatoregex #cfg #pda #undecidable #ricestheorem Questions came from: https://bit.ly/3iET8FQ 00:00:00 GATE 2019 00:07:12 GATE 2020 00:14:36 GATE 2018 00:22:29 GATE 2017 (Set 1) 00:33:37 GATE 2017 (Set 2) 00:40:55 GATE 2016 (Set 1) 00:49:18 GATE 2016 (Set 2) 00:54:51 GATE 2015 (Set 1) 01:03:12 GATE 2015 (Set 2) 01:08:30 GATE 2015 (Set 3) 01:11:30 GATE 2014 (Set 1) 01:12:35 GATE 2014 (Set 2) 01:19:19 GATE 2014 (Set 3) 01:24:52 GATE 2013 01:28:16 GATE 2012 01:31:21 GATE 2011 01:33:43 GATE 2010 01:38:43 GATE 2009 01:44:18 GATE 2008 01:59:17 GATE 2008 (IT) 02:08:25 GATE 2007 02:11:20 GATE 2007 (IT) 02:22:19 GATE 2006 02:28:33 GATE 2006 (IT) 02:38:00 GATE 2005 02:42:30 GATE 2005 (IT) 02:55:50 GATE 2004 02:57:58 GATE 2004 (IT) 03:02:57 GATE 2003 03:11:42 GATE 2002 03:42:39 GATE 2001 03:14:32 GATE 2000 03:17:39 GATE 1999 03:20:42 GATE 1998 03:27:31 GATE 1997 03:29:34 GATE 1996 03:35:00 GATE 1995 03:38:13 GATE 1994 03:39:40 GATE 1992 03:47:22 GATE 1991 Patreon: https://bit.ly/3ebTFvi Twitch: https://bit.ly/2ZQvvkV Mixer: https://bit.ly/3fdn6yr Discord: https://bit.ly/2CdSMp4 Facebook: https://bit.ly/323B4iZ Twitter: https://twitter.com/EasyTheory Teespring: https://bit.ly/3iFHCdf If you like this content, please consider subscribing to my channel: https://www.youtube.com/channel/UC3VY6RTXegnoSD_q446oBdg?sub_confirmation=1 ▶SEND ME THEORY QUESTIONS◀ ryan.e.dougherty@icloud.com ▶ABOUT ME◀ I am a professor of Computer Science, and am passionate about CS theory. I have taught over 12 courses at Arizona State University, as well as Colgate University, including several sections of undergraduate theory. ▶ABOUT THIS CHANNEL◀ The theory of computation is perhaps the fundamental theory of computer science. It sets out to define, mathematically, what exactly computation is, what is feasible to solve using a computer, and also what is not possible to solve using a computer. The main objective is to define a computer mathematically, without the reliance on real-world computers, hardware or software, or the plethora of programming languages we have in use today. The notion of a Turing machine serves this purpose and defines what we believe is the crux of all computable functions. This channel is also about weaker forms of computation, concentrating on two classes: regular languages and context-free languages. These two models help understand what we can do with restricted means of computation, and offer a rich theory using which you can hone your mathematical skills in reasoning with simple machines and the languages they define. However, they are not simply there as a weak form of computation--the most attractive aspect of them is that problems formulated on them are tractable, i.e. we can build efficient algorithms to reason with objects such as finite automata, context-free grammars and pushdown automata. For example, we can model a piece of hardware (a circuit) as a finite-state system and solve whether the circuit satisfies a property (like whether it performs addition of 16-bit registers correctly). We can model the syntax of a programming language using a grammar, and build algorithms that check if a string parses according to this grammar. On the other hand, most problems that ask properties about Turing machines are undecidable. This Youtube channel will help you see and prove that several tasks involving Turing machines are unsolvable---i.e., no computer, no software, can solve it. For example, you will see that there is no software that can check whether a C program will halt on a particular input. To prove something is possible is, of course, challenging. But to show something is impossible is rare in computer science, and very humbling. May 25, 2020 at 05:00PM

[showwaysnow]

Sacred Geometry Software — OmniGeometry

Learn how you can create your own Sacred Geometry art, designs and mandalas in only a few minutes using our interactive Recursive Geometry Generator. https://showwaysnow.com/sacred-geometry-software-omnigeometry/ #AdobePhotoshop, #ComputabilityTheory, #ComputerProgramming, #Computing, #Designer, #DesignerSoftware, #DivideAndConquerAlgorithm, #FlowerOfLife, #ImageEditingSoftware, #Mandalas, #Merkaba, #MutualRecursion, #NassimHaramein, #Recursion, #ResonanceProject, #SacredGeometry, #SacredGeometrySoftware, #SeedOfLife, #SelfReference, #SoftwareEngineering, #TechnologyInternet, #TheoreticalComputerScience, #TheoryOfComputation #BestSoftwareServicesProvider

[go-classes]

If you relate to it, then you have Not studied TOC from GO Classes #GateCSE Complete Course: https://www.goclasses.in/s/pages/gatecompletecourse @goclasses_cse #toc #theoryofcomputation #goclasses #goclassesmemes #gateoverflow #gatecs #gate2023 #gate2022 #gatecsit #automatatheory #computerscience #gate #gateexam https://www.instagram.com/p/CjN3rghvtu-/?igshid=NGJjMDIxMWI=

[nvas]

I/O Complexity

Today I came across a very interesting post on I/O Complexity, an additional way of characterizing the complexity of a computation. The following abstract, to tease you out, is from Robert Harper's Existential Type blog (his full article is here). Relevant is the slideshow on Cache- and IO-Efficient Functional Algorithms.

This summer Guy Blelloch and I began thinking about other characterizations of the complexity of programs besides the familiar abstractions of execution time and space requirements of a computation.  One important measure, introduced by Jeff Vitter, is called I/O Complexity.  It measures the efficiency of algorithms with respect to memory traffic, a very significant determiner of performance of programs.  The model is sufficiently abstract as to encompass several different interpretations of I/O complexity.  Basically, the model assumes an unbounded main memory in which all data is ultimately stored, and considers a cache of  blocked into chunks of size  that provides quick access to main memory.  The complexity of algorithms is analyzed in terms of these parameters, under the assumption that in-cache accesses are cost-free, so that the only significant costs are those incurred by loading and flushing the cache.  You may interpret the abstract concepts of main memory and cache in the standard way as a two-level hierarchy representing, say, on- and off-chip memory access, or instead as representing a disk (or other storage medium) loaded into memory for processing.  The point is that the relative costs of processing cached versus uncached data is huge, and worth considering as a measure of the efficiency of an algorithm.

[go-classes]

Want to "Understand" TOC?? Join GO Classes TOC course Or Goclasses Complete GATE Course (Visit Goclasses Website) : https://www.goclasses.in/s/store/courses/description/Theory-of-Computation-2023 Join Our Telegram Group for #Doubts Discussions: Username: GATECSE_Goclasses https://t.me/GATECSE_Goclasses #GoClasses #gate #gatecse #goclassesmemes #toc #automatatheory #theoryofcomputation #gatecs #gateexam #gate2023 #gate2024 #gate2025 #algorithms #computerscience #computersciencememes #gate2022 #Gateoverflow #gatememes #mathematics #memes #meme #csememes https://www.instagram.com/p/ChZwDWMF2vK/?igshid=NGJjMDIxMWI=

[smartcherryposts]

Theory Of Computation - Practice Questions On Language

If You Have the Ability To Think About A Problem These Problems Are Damn Eay For You, Lets Understand And Solve The Questions About Language In Theory Of Computation. Before Solving Questions I Hope You Understood About Language Which I Explained In Previous Post, If You Have Not Read, Click Here If You Know About Language Already, let's Solve The Questions On Language

  Q) Choose The Correct Statement From The Following. a) Every Regular Language Is Finite b) Every Non-Regular Language Is Finite c) Every Regular Language Is Infinite d) Every Non-Regular Language Is Infinite   Answer - d) Every Non-Regular Language Is Infinite Explanation - If You See The Language Hierarchy, Every Non-Regular Language Is Infinite

  Q) Which Of The Most Appropriate Answer For Finite Language. a) L Is Regular b) L Is CFL c) L Is CSL d) L Is REL   Answer -  L Is Regular   Explanation - Yes, L Is Regular Is The Most Appropriate Answer Because CFL, CSL, REL May Or May Not Be Appropriate.

Read the full article

[smartcherryposts]

Theory Of Computation Practice Questions

We Can Understand The Relation Between The Machines And The Expressive Power Of Each Automata By Seeing Above Picture. But With What Basis The Above Relation Is Made. Why Finite Automata Is Less Than Pushdown Automata And Why Pushdown Automata Is Less Than Linear Bounded Automata And Why Linear Bounded Automata Is Less Than Turing Machine. Let's Understand. Why Pushdown Automata Accepts More Languages Than Finate Automata? Why Turing Machine Accepts Accepts More Languages Than Pushdown Automata?      

FINITE AUTOMATA

FA -> FA + 0 Stack

In Finite Automata There Is A Stack Memory, Where I Don't Use Extra Memory Other Than Stack Memory. Like Whatever Memory Needed For States And Transitions, I'll Have In Finite Automata. If I Want Perform Extra Task, I'll Not Have Extra Memory, That Is Why FA -> FA + 0 STACK Finite Automata = Finite Automata + 0 Stack ( 0 Stack Means Without Anyother Memory) Finite Automata Is Independent, Which Have Stack Memory.  

PUSHDOWN AUTOMATA

PDA -> FA + 1

Pushdown Auotmata Accepts More Languages Than Finite Automata. In Pushdown Automata - Finite Automata + 1 Stack Memory Will Be There. PDA -> FA + 1 Stack    // Here 1 Stack Memory Will Be Added In PDA, The Languages Which Are Not Accepted By Finite Automata, Those Languages Maybe Accepted By PUSHDOWN AUTOMATA  

Turing Machine

Turing Machine - FA + 2 STACK There Are Languages Which Are Not Accepted By Pushdown Automata, Those Languages Are Accepted By Turing Machine. TM= FA + 2 STACK //  In Turing Machine, 2 Stack Memories Attached, For Accepting More Languages, If I Add Finite Auotmata With 2 Stack Memories, It Becomes Turing Machine.   I'm Not Telling You About Linear Bounded Automata(LBA) Because Still Research Is Going On On LBA.That Is Why The Reason I'm Not Telling You About LBA Here.   Basically, You Have To Understand Why TM Is So Much Powerful, It Has FA With 2 Stacks Memory.It Has More Memory.   Do You Have Doubt What Is ->  FA + 3 Stacks ? This Is A Turing Machine.   There Is No Difference Between FA+2 STACKS & FA + 3 STACKS   FA+2 STACKS And FA + 3 STACKS Both Are Same Powerful. If I Say FA + n Stacks ( n≥2 )   All Are Same Powerful. FA+2 STACK & FA + 3 STACK & FA + n STACK , All Are Equally Powerful. Example E(FA+2 STACK)=E(FA+n STACK) //Expressive power of FA + 2 STACK Is Equal To Expressive Power Of FA + n STACK   This Is Basically Called As RAM,If You Increase The Memory Of The RAM, It Can Accept Same Number Of Languages. In Simple Words ' The Same Number Of Languages For Will Be Accepted Even If You Increase Or Decrease The RAM Size.

AUTOMATA

I Have Divided Automata Into Three Parts,1) LA 2) LG 3) COMPUTATIONAL MODEL   Language Acceptor LA Means Language Acceptor, If I Give Language As Input To Any Machine, Machine Gives Me Output Like ' YES ' Or ' NO ' Means Language 'Accepted' Or 'Rejected'   I Have Three Machine FA, PDA, TM. In these Models, Some Will Be LA ( Language Acceptor ), They Accept Or Reject Languages.   Language Generator I Have Three Machine FA, PDA, TM. In These Models, Some Will Accept-Languages And Generate Different Languages. Those Type Of Auotmata Are Called As Language Generator Automata, This Model Is Called Language Generator.   Computational Model If I'm Giving Input String To The Machine And If I'm Getting Result From That Machine, If I'm Getting A Computational Value Back As Result. For Example If Im Giving   2+3  // As Input The Calculator Gives Me Result 5. // Means I'm Getting A Value In Return As Output As Result. This Model Is Called As Computational Model.   On These Three Model, LA, LG, Computational Model, I Have Divided My Automata.

  Finite AUTOMATA FA Is Language Acceptor And Computational Model. I Dont Use FA As A Language Generator Because It Will Not Generate Any Language. Pushdown AUTOMATA PDA Is Only Language Acceptor. If I give String As Input,If My String Is Satisfying The Language Of Automata, Then My PDA Will Goto Final State Or Else It Will Goto Non-Final State. PDA Will Not Give Any Result,It Will Not Give Result By Doing Any Computation. PDA Is A Only Language Acceptor. TURING MACHINE Turing Machine Accepts All My Models.LA, LG, CM All The Three Models. Turing Machine Can Do Every Task Which Computer Performs.

    Practice Questions

5) Which Of The Following Is Wrong?

a) FA + 1 STACK  Is More Powerful Than FA B) FA + 2 STACK Is More Powerful Than FA + 1 STACK c) FA + 3 STACK Is More Powerful Than FA + 2 STACK d) NOTA   Answer - c)   Explanation -

  6) Which Of The Following Model Doesn't Work As Transducer?

a) FA b) PDA c) TM d) NOTA   Answer - b)   Explanation -  The Meaning Of Transducer Is Translating, Taking Input In A Form And Giving Output In Another Form.

PDA Is Only An Acceptor Not A Result Giver, So PDA Is Not A Transducer, Which Will Not Give Output.   Share This Post With Your Friends If You Love The Explanation.             Read the full article

[smartcherryposts]

Theory Of Computation Practice Questions

Theory Of Computation Practice Questions Solved And Explained Briefly.  

Which Of The Following Statement Is Correct?

a) DFA Is More Efficient Than NFA b) NFA Is More Efficient Tham Than DFA c) DFA Is More Powerful Than NFA d) NFA Is More Powerful Than DFA   Answer Is a) Explanation 

E(NFA)=E(DFA) Expressive Power Of NFA Is Equal To DFA, The Languages Accepted By NFA Are Equal To The Languages Accepted By DFA. I Can Draw NFA For All RL. I Can Draw DFA For All RL.   Hence DFA Is More Efficient Because I'll Have Only One Router Or Way.  

2) Choose The Incorrect Statement From The Following.

a) DPDA Is More Efficient Than NPDA b) Capabilities Of DPDA & NPDA Are Same c) NPDA Is More Powerful Than DPDA. d) NOTA   Answer - b Explanation

E(NPDA)≥E(DPDA)  

3) For Which Of The Language An Automata Can Be Constructed In Both Deterministic And Non-Deterministic Mode To Accept That Language.

a) Regular b) CFL c) REL d) NOTA   Answer - a) & c)   Explanation a)E(NFA)=E(DFA)

b) E(NPDA) ≥ E(DPDA)

c) E(NTM)=E(DTM)

d) ×  

4) Choose Correct Statement From The Following

a) DFA Is More Powerful Than DPDA b) DPDA Is More Powerful Than DFA c) NFA Is More Powerful Than NPDA D) NOTA   Answer - b)   Explanation

a) FA Read the full article

[smartcherryposts]

Types Of Languages - Types Of Grammars - Types Of Automata(Machine)

Types Of Languages - Every Language Have Two Components, One Is Grammer And Another One Is Acceptor Or Machine. Grammer Generates Language, Acceptor Accepts The Language, Acceptor Is A Machine.

If The Language Changes Then Its Grammer Is Also Changes, If The Language Changes The Machine Also Changes, Which Accepts The Language. We'll Understand The Types Of Languages.

Types Of Formal Languages

According To The Memory, According To The Grammer And Change In Grammer, Are The Reasons For To Have Different Language Necessarily. Let Know Why To Have Different Languages. To Accept A Language Few Machines Needs Memory, Few Machine Don't Need Memory In It To Accept-Language. According To The Machine Architecture Or According To The Machine Model, I Have Divided Languages Into Different Types. Based On The Grammer I Have Divided Languages Into Different Types.   First Language In Types Of Formal Languages Is Regular Language, In ShortCut, I'm Writing Regular Language As RL RL Means Regular Language Remember This, In Theory Of Computation We Mostly Use Shorts Cuts. I Use Regular Language, I Don't Need Memory Size In The Machine For This Language.   Second Is Context Free Language (CFL) Context Free Grammer Is Little Different Compare To Regular Language, I Need To Use Stack Memory For Context Free Grammer. Third Is Context-Sensitive Language (CSL) I Need To Use More Than One Memory In Context-Sensitive Language, Fourth Is Recursive Enumerable Language (REL)   According To The Machine Architecture, According To The Grammer I Have Divided Languages Into Four Types. According To The Memory Size And Memory Model These Are Types Of Languages, These Are The Types Of Languages We Have.  

Types Of Grammars

The Set Of All The Rules Which Are Used For Generate A String Is Known As Grammer. I Have Follow Few Conditions To Generate A String, Those Conditions Are Created By Grammer. Example - Few Rules I'm Writing Here S->AB // S Gives AB, S Means Starting Symbol,If I Want To Create A String, I Have Start, So This Is The Symbol For Starting A String. And Which Is Denoted With Capital Letters, We Call These Capital Characters As Non- Terminals Or Variables, In C Language You Will See Variables, Similarly Here These Variable Values Can Be Changed.   A->a // A Gives Small a, The Small Characters, Can Be Seen On Left Side, Those Are Called Terminals, Terminals Means We Cant Expand These And We Cant Change, If I Get ' a ' In A String, I Can't Change That 'a ', Whereas If I Get " AB " In Any String, I Can Replace It With      ' a ', That's Why We Call S->AB As Variables And ' a ' As Terminals.   B->b // B Gives Small b   For Example - If I Want To Create A String, I Have Input Alphabets Σ= {a,b}, I Have To Create String Using 'ab', By Using The Above Grammer Rules Can I Create A String ?? Lets See

Using The Given Set Of Rules Of Grammer We Created A String ' ab ' ' S ' Is My Starting Symbol, Always I Need To Start With Starting Symbol ' S ' Then I Need To Replace ' S ' With The Variable I Have On The Left Side Of ' S ' i.e ' AB ' , In The Place Of ' AB ' It Is Possible To Have Variables And Non- Variables And Terminals. I Replaced ' S ' With The Variables ' AB '   I Have A Set A Rule i.e A - > a, In Which A Replaces ' a ' , i Replaced ' A ' With ' a ' Similarly B- > a , I Replaced b In The Place Of B   If You Traverse The String, The Charecters Came In The Leaf Node, That Combination We Call As " String " So ab Is The String I Have Generated.   'ab' Is The String Generated Using The Set Of Rules Of Grammer Given And By Taking The Input Alphabets Σ={a,b} And That String Gets Satisfied For That Language Of That Grammer. Like That Grammer Rules Are Written In This Way.   Types Of Grammer Regular Grammer (RL) Context Free Grammer (CFG) Context Sensitive Grammer (CSG) Recursive Enumerable Grammer (REG) Or Unstructured Grammer.   According To The Language, I'll Have Its Own Grammer, Every Language Has Its Own Grammer.If I Create A String Using A Particular Grammer, That Required String Represent Its Language.  

Types Of Automate (Machine)

The Language I'm Talking, To Accept That Language,It Need's A Machine It Needs A Mathermatical Model. Why I Need Machine? Lets Understand With An Example.   Imagine That I Have Took A Language Called L. L= Set Of All The Strings Starts With ' a ' // Means All The Strings In The Language Starting Symbol Should Be ' a ' Input Alphabets Σ = {a,b} ={a,ab,aab,aba,abb,aaab,abbab,.....} // Generated Strings I Can Create Infinite Strings In This Language. I Can Create Any Number Of Strings Using Starting ' a ' Symbol. I'll Store All These Strings In Machine.   Imagine That I Need To Search For A String Which Satisfies This Language. If I Give A Input String 'aba'  To Machine And I'll Ask Machine To See The String Is There Or Not In The Language ' L '   Machine Searches ' aba ' String In All The Stored Stored Strings Where It Is There Or Not.   I Want To Talk Practically, There Are Infinite Strings Which Accepts The Language ' L ' In The Machine, Storing Large Number Of Strings In My Machine Is Little Difficult Because Every Machine Has A Problem Called Memory.I'll Have Limioted Amount Of Storage Capacity, I Cant Store Infinite Number Of Data.   So, If I Get Any String As Input, I Need A Mechanism With Which I Can Judge That Wheather This String Satisfies My Language Or Not. So,I Need To Create A Machine Which Gives Output As " Yes " Or " No".   Thats Where, What Will Be The Input For My Machine? My Machine Input Will Be 'Language' And Input String. And What Should I Create? I Should Create A Finite Machine. Finite Machine Means, Where Finite Number Of Decisions Taking Ability Will Be There And Finite Number Of States Will Be Available. Which Gives Me "Output" Saying That "This String Is In This Language" Or Not   If I Can " I Can Also Store All The Infinite Strings Of The Language In My Machine" And Whenever I Get A Input I Can Do Searching Operation To Find The Input String From The Stored Strings. But My Language Is Infinite,That's Why I Cant Store Infinite Data In Finite Memory. So, I Need A Type Of Representation, Which We Call It As Finite Machine.   We Call That Finite Machine As Finite Automata In This Theory Of Computations(Automata), We Need To Create Lot Of Automata( Machine)

If You Observe The Picture, The FA(Finite Automata) Takes Input As Language And Gives Out Put As ' Yes ' or ' No ' For This Language If The Input String Given To The Automata Is Valid Or Acceptable To It, Then My Finite Automata Gives Output As ' Yes ' If The The Input String That Doesn't Satisfy The Language, That Doesn't Satisfy The Restrictions Of The Language,For That Finite Automata Gives Output As ' No ' So According To The Language, I Have To Change The Machine,If My Language Is Finite Language, My Machine Is Finite Automate Because Finite Automata Accepts Finite Language. If The Language And Its Grammer Changes, If I Require Memory, I Need To Attach Memory To Finite Automata(Machine) To Accept Those Languages. According To That, My Machine Is Divided Into Different Types.   Types Of Automata Finite Automata (FA) PushDown Automata (PDA) Linear Bounded Automata (LBA) Turing Machine According To The Memory Requirement, Memory Attachment, We Divided It Into Different Types. 1.Finite Automata In Finite Automata, There Will Be Finite Number Of States. We won't Attach Any Memory To This. 2.Push Down Automata Here I Also Required Stack Memory, Because Few Languages Will Get Accepted By Push Down Automata, So One Stack Memory Gets Attached To It. 3.Linear Bounded Automata Here Also I Need I Required One More Stack Memory Because The Languages Accepted By Linear Bounded Automata, There I Will Be Required More Memory. 4.Turing Machine Turing Machine Is Big Machine Among All. Turing Machine Is Also Called Abstract Model Of Computer Because Whatever The Problem's Can Be Solved By Turing Machine, All Those Problems Can Be Solved By Computer.   So This Is The Information About Automata(Machine), Grammars And Languages.   If You Like The Explanation, Install Smart CSE Android App From Google Play Store, So That You Can View All The Topics Of Theory Of Computation In Your Mobile.

  Thanks                               Read the full article