#Traverse Undirected Graph

[codingprolab]

CS2420 Program 7  USU Walk Cleaning Problem

A sweeper  must be used to remove the debris from all the sidewalks at USU.  We want to find the cheapest way of traversing all walkways. We construct a graph of the sidewalks. If that graph has an Euler tour, all edges can be visited exactly once – which is guaranteed to find the  most efficient way of cleaning the paths.   We know that we can easily determine if an undirected graph has an Euler…

[programmingandengineering]

Homework 4: Graph Algorithms: Part I

Problem 1: Graph Traversal 50 points Demonstrate both breadth-first search (BFS) and depth-first search (DFS) algorithms (with v1 as the start node) on the unweighted, undirected graph shown in Figure 1. Clearly show how each node-attribute (including frontier) changes in each iteration in both the algorithms. (20 points) Implement both BFS and DFS algorithms in Python using a graph class based…

[myprogrammingsolver]

HW4: Graphs, Traversals

Q1. Given an undirected graph with 10 vertices but 45 edges, which of the following will be true? Select all that apply. Every node will have at least one neighbor The graph will have duplicate labels An Adjacency List would be more space-efficient to represent this graph vs. a Matrix The graph is GUARANTEED to have a cycle in it None of the above A and D are true. Q2. There are N cities,…

[nullset2]

Minimum Spanning Tree -- Connect Islands with Minimum Bridges Problem

Certain problems in Computer Science can be solved with a Minimum Spanning Tree. A minimum spanning tree is a tree derived from a weighted, undirected graph, which connects all of the nodes in that graph using the least sum of weights possible.

Prim's algorithm works in a greedy manner, producing an MST for a graph by comparing distances in a BFS manner and picking the smallest one at every step of traversal.

It works by producing an adjacency matrix to represent a graph and the distances between every node (necessarily, a graph with a "cut" in the middle; think of it as an identity matrix, but with zeroes in the main diagonal rather than ones, and symmetrical values populated otherwise). This matrix usually looks like this:

[0.0, 1.0, 6.0, 3.0, 5.0, 7.0, 8.0, 9.0] [1.0, 0.0, 5.0, 2.0, 4.0, 6.0, 7.0, 8.0] [6.0, 5.0, 0.0, 5.0, 3.0, 1.0, 4.0, 3.0] [3.0, 2.0, 5.0, 0.0, 2.0, 4.0, 5.0, 6.0] [5.0, 4.0, 3.0, 2.0, 0.0, 2.0, 3.0, 4.0] [7.0, 6.0, 1.0, 4.0, 2.0, 0.0, 3.0, 2.0] [8.0, 7.0, 4.0, 5.0, 3.0, 3.0, 0.0, 1.0] [9.0, 8.0, 3.0, 6.0, 4.0, 2.0, 1.0, 0.0]

The distances used can be Pythagorean distances or Manhattan distances (sum of absolute values of differences between coordinates).

Then, you build THREE auxiliary arrays:

One to represent the parents of every node of the adjacency matrix.

One to represent the weights connecting the final MST, which we will call the "key" row.

One to mark a given node in the MST as visited.

Then, these are the instructions:

Start from node 0; mark as visited and its weight as 0.

Mark its parent as NULL (-1 in this case).

Make a comparison of all of the weights towards the nodes it's connected to. Take the smallest one, add it to the weights, move onto that node, and repeat until you exhaust all the nodes.

This is a Java implementation, using the "Islands and Bridges" problem: https://gist.github.com/nullset2/a101d39f3bdc1b3670a948e0e8416df1

Thank you!

[codezclub]

C Program for Traversing an Undirected Graph through BFS

Traversing an Undirected Graph through BFS Write a C Program for Traversing an Undirected Graph through BFS. Here’s simple C Program for Traversing an Undirected Graph through Breadth First Search(BFS). Breadth First Search (BFS) BFS is a traversing algorithm where you should start traversing from a selected node (source or starting node) and traverse the graph layerwise thus exploring the…

[creativecoding]

Graphs and decision trees in Python

A pair of nodes are connected by a single path.

Decision trees are great for finding solutions. The trunk is at the top and the the branches at the bottom - very Australian.

But, how are decision trees useful?

(Computer) networks require algorithms to move information around.

Financial networks - moving around money

Sewage networks - moving water around

Decision trees can determine which path to take when executing the algorithm that moves information.

Graphs

Graphs can capture interesting relationships with this data.

The min flow or max cut problem identifies which clusters in a graph have a lot of interaction between each-other but not with many (or any) other clusters.

Inference option. Is there a sequence of edges to get from A to B. Can I find the least expensive (meaning shortest) path?

The graph partition problem. Not all nodes have connections with every other node.

This is finding and isolating different sets of connections.

Min cut max flow - an efficient way of separating highly connected elements, the things that connect a lot in a sub-graph.

Graphs (graph theories) are used by us everyday in the forms of travel maps such as on the tube etc.

Di graph (directed graph) the edges pass in one direction - almost obvious, I know.

Nodes or vertices become points of intersections, places to make a choice or has terminals.

Edges would be connections between points - the roads on which we could drive. Each edge would have a weight.

Choices that remain:

What’s the expected time between a source and a destination?

What’s the distance between the two?

What’s the average speed of travel?

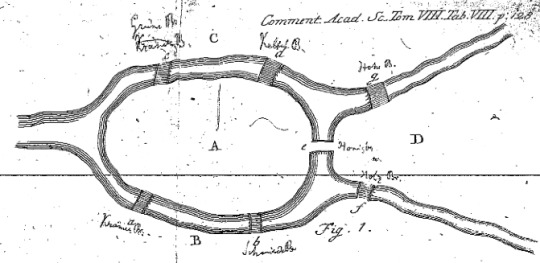
Thinking about navigation in graph systems incorporated within history from 1700′s. The image above is from ‘Solutio problematis ad geometriam situs pertinentis,’ Eneström 53 [source: MAA Euler Archive]

Bridges of Königsberg which has seven bridges that connect it’s rivers and islands - is it possible to take a walk that traverses each of the seven bridges exactly ONCE.

Leonhard Euler, a great Swiss mathematician said, “make each island a node, each bridge is an undirected edge”.

This eliminates irrelevant details about the size and focuses on the connections present, testing the point of crossing only once.

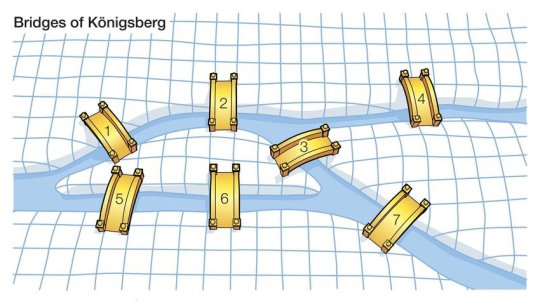
Euler's Proof and Graph Theory

When reading Euler’s original proof, one discovers a relatively simple and easily understandable work of mathematics; however, it is not the actual proof but the intermediate steps that make this problem famous.  Euler’s great innovation was in viewing the Königsberg bridge problem abstractly, by using lines and letters to represent the larger situation of landmasses and bridges.  He used capital letters to represent landmasses, and lowercase letters to represent bridges.

This was a completely new type of thinking for the time, and in his paper, Euler accidentally sparked a new branch of mathematics called graph theory, where a graph is simply a collection of vertices and edges.

Today a path in a graph, which contains each edge of the graph once and only once, is called an Eulerian path, because of this problem. From the time Euler solved this problem to today, graph theory has become an important branch of mathematics, which guides the basis of our thinking about networks.

An easy graph would be: latitude and longitude

We want to extract things away from the graph so let’s represent the nodes as objects - using classes for these.

For now, the only information to store a name (which is currently just a string) inherits from the base Python object class.

Init function used to create instances of nodes.

Store inside each instance - in other words inside of self - under the variable name of whatever was passed in as the name of that node.

If we have ways to create things with a name we need ways to get them back out. So we can select it back out by asking an instance of a node “what is your name?” by calling getName, it will return that value.

Within the class edge we’d see:

class           Edge(object):

              def _init_(self, src, dest):

                    “““Assumes src and dest are nodes”““

                    self.src = src

                    self.dest = dest

             def getSource(self) :

                    return self.src

             def getDestination(self) :

                   return self.dest

            def _str_(self):

                  return self.src.getName() + ‘->’\

                            + self.dest.getName()

To print things out we’re just gonna print name. This allows us to create as many nodes as we like.

Edges connect up two nodes - allowing us to create a fairly straightforward construction of a class. Again, it’s going to inherit from the base Python object. To create an instance of an edge we will assume in the example above that the arguments passed in (source and destination) are nodes.

This is shown after the init function.

Not names, nodes - the actual instances of the object class. So inside of the edge, we set internal variables for each instance of the edge source and destination. The get source and destination allows us to get those variables back out. The last part asks to print the name of the source then an arrow and then the destination.

So here, given an instance of an edge, we can print it and it will retrieve the source or the node associated with the source inside the instance. The opened and closed parens () is used to call it.

From this we can decide how to represent the graph, starting with a di-graph which has edges that pass in once direction. Given all the sources and all the destinations we can just create an adjacency matrix.

[programmingsolver]

Assignment 9 - Graphs

OBJECTIVES   Build an undirected weighted graph   Perform Breadth First Traversal (BFT) and Depth First Traversal (DFT)   Overview   You were just a humble map programmer, but that was before the zombies attacked! Now, your skills are put to coordinating the survivors and finding routes between cities that haven’t been overtaken. Some of the roads between these cities have been overrun and…

[kitwallace]

Finding Eulerian circuits

As discussed previously, Eulerian circuits are useful in 3D printing because they enable continuous extrusion which increases the strength of the printed object . In addition the lack of a seam improves its visual appearance.  

However finding a Eulerian circuit in a design is not always easy, and finding the ‘best’ even harder.

For a rectangular grid  (3 x 2) 

a braiding program I developed a while ago finds a circuit.  It attempts to find a braid on an N x M grid.  If N and M are relatively prime, one rope (ie. a Eulerian circuit) completes the grid  but if not (like this 6 x 3), multiple ropes are needed.

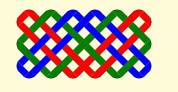
This restriction on the size of this mesh is not helpful.  Since every N x M mesh of this style is Eulerian, they must all have a Eulerian circuit. This could  be constructed if we were able to join up the separate partial loops. Start somewhere and follow a chain of unvisited edges until you get back to the start.  If all edges have been visited, you are done. If not, go back to the last vertex with unvisited edges and start a new circuit at that point, with those points inserted into the current circuit .This is the Hierholzer algorithm.

Hierholzer algorithm

I searched for a pseudo code implementation but wasn’t satisfied with any that I found.  Any implementation depends heavily on the data structures used: for the graph itself in a form in which edges can be removed as they are visited and for the path as it is constructed, adding a vertex to the end and rotating the path to backtrack. 

One representation of a graph with V vertices and E edges is as a V x V adjacency matrix where adj[i,j] =1 indicates the edge i to j which will be symmetric across the diagonal if the graph (as here) is undirected.  Updating is straightforward but  navigating from vertex to vertex requires a scan through a row.  

Alternatively, the graph can be represented as an array of lists of the connected vertices  - easy to navigate, more compact for a sparse graph (as these are)  but harder to update.  

The JavaScript array structure can implement the vertex list and the evolving path. I found this is a useful summary of operators. push() and pop()  will add and remove the head of the list;  unshift() and shift() do the same at the tail of the list.  myArray[myArray.length - 1] and myArray[0] return the head and tail of the list respectively.

Minimizing turns in the circuit

The Hierholzer algorithm mechanically selects the next vertex by taking any vertex (the first or the last perhaps) from the list of possible vertices. This does find a circuit but not necessarily a good circuit.  For the purposes of 3D printing, good means a circuit with a minimum number of turns since straight runs will be stronger and faster.  To get a good, though not necessarily the best, circuit, I added a kind code to each edge and then choose a vertex in the same kind if possible.  For the rectangular mesh above, there are two kinds , coded +1 for the right diagonal, -1 for the left.  (note that we don’t need to distinguish between the direction of travel on a diagonal since we can’t reverse direction at a vertex as that edge has just been traversed)

JavaScript Implementation

In the Fottery suite, the algorithm is implemented as a method in a Graph class which includes the adjacency structure adj and supporting functions:

find_circuit(kind-0,start_vertex = 0 ) {    // assumes graph is connected and a euler circuit exists         var cpath =[];        var vertex, next_vertex, edge, edges;        cpath.push(start_vertex);        while (cpath.length < this.n_edges  ) {            vertex = cpath[cpath.length - 1];  // the last vertex in the constructed path            edges = this.adj[vertex];  // get its  adjacent nodes (untraversed edges)            if (edges.length == 0) {  // if no untraversed edges                cpath.pop();   // rotate back to the previous vertex                if (!(vertex == initial_vertex && cpath[0]==vertex)) { // dont  include the start at the end                  cpath.unshift(vertex);                 }            } else {                  edge = this.best_edge(edges,kind);                  next_vertex= edge[0];                kind = edge[1];                cpath.push(next_vertex);  // add  vertex to the path                this.remove_edge(vertex,next_vertex); // remove the traversed edge            }         }

       // get start back to the first in the path        while (cpath[0] != start_vertex)                  cpath.push(cpath.shift());        return cpath;

[damn discovered a use-case where this implementation fails!   

16 April 2024 - fixed edge case with the bold change ] 

Example

A  rectangular N x M  mesh like the one above is more useful if the vertices at the edges are connected to make a border.  This addition does not change the Eulerian nature of the graph, but introduces two more directions, horizonal and vertical.  This is the resultant 2 x 3 mesh.

and this a box constructed from rectangular meshes.  The sides are bevelled by insetting the top layer from the bottom by the thickness of the tile to make a 45 degree bevel.  Assembled with plastic glue (UHU).

Stars (stellated polygons)

This algorithm has been applied to other structures such as a triangular mesh and stars.   

A pentagram can be constructed with 5 vertices and 5 edges connecting pairs of vertices.This is a closed path so Eulerian.

A hexagram looks Eulerian, but if constructed by connecting the vertices of the star, the graph is not connected (two separate triangular paths).

To make a circuit so it can be printed continuously, we have to compute the 6 intersections and the 18 edges (of 3 kinds)  which result from the intersections, and then use the modified Hierholzer algorithm to find a good circuit.  

A fully connected star is only Eulerian if the number of vertices is odd - which makes for a kind of infill pattern.

Nearly Eulerian graphs

Structures which are Eulerian are rather limited. An hexagonal tiling is not Eulerian because vertices are order 3. However it and many others are nearly Eulerian in the sense that small modifications to the graph will make the graph Eulerian. The basic idea is to duplicate ( the minimum number of ) edges. If this is a problem with printing, the edge could be omitted or an additional edge inserted.

This problem  is called the Chinese Postman Problem or Route Inspection Problem and the subject of extensive research. 

This is work for another day -.April 2024 see Non-Eulerian graphs

References

Fleischner, Herbert (1991), "X.1 Algorithms for Eulerian Trails”   https://archive.org/details/euleriangraphsre0001flei/page/

Gregory Dreifus,Kyle Goodrick,Scott Giles,Milan Patel Path Optimization Along Lattices in Additive Manufacturing Using the Chinese Postman Problem June 2017  https://www.researchgate.net/publication/317701126_Path_Optimization_Along_Lattices_in_Additive_Manufacturing_Using_the_Chinese_Postman_Problem

Prashant Gupta, Bala Krishnamoorthy, Gregory Dreifus  Continuous Toolpath Planning in a Graphical Framework for Sparse Infill Additive Manufacturing  April 2021 https://arxiv.org/pdf/1908.07452.pdf

https://algorithms.discrete.ma.tum.de/graph-algorithms/directed-chinese-postman/index_en.html

https://www.stem.org.uk/resources/elibrary/resource/31128/chinese-postman-problems

https://ibmathsresources.com/2014/11/28/the-chinese-postman-problem/

http://www.suffolkmaths.co.uk/pages/Maths%20Projects/Projects/Topology%20and%20Graph%20Theory/Chinese%20Postman%20Problem.pdf

[holytheoristtastemaker]

Have you ever solved a real-life maze? The approach that most of us take while solving a maze is that we follow a path until we reach a dead end, and then backtrack and retrace our steps to find another possible path. This is exactly the analogy of Depth First Search (DFS). It's a popular graph traversal algorithm that starts at the root node, and travels as far as it can down a given branch, then backtracks until it finds another unexplored path to explore. This approach is continued until all the nodes of the graph have been visited. In today’s tutorial, we are going to discover a DFS pattern that will be used to solve some of the important tree and graph questions for your next Tech Giant Interview! We will solve some Medium and Hard Leetcode problems using the same common technique. So, let’s get started, shall we?

Implementation

Since DFS has a recursive nature, it can be implemented using a stack. DFS Magic Spell:

Push a node to the stack

Pop the node

Retrieve unvisited neighbors of the removed node, push them to stack

Repeat steps 1, 2, and 3 as long as the stack is not empty

Graph Traversals

In general, there are 3 basic DFS traversals for binary trees:

Pre Order: Root, Left, Right OR Root, Right, Left

Post Order: Left, Right, Root OR Right, Left, Root

In order: Left, Root, Right OR Right, Root, Left

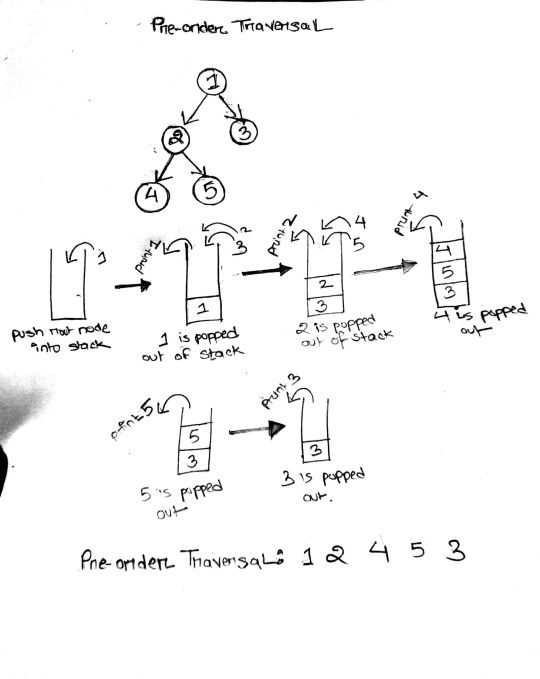
144.  Binary Tree Preorder Traversal (Difficulty: Medium)

To solve this question all we need to do is simply recall our magic spell. Let's understand the simulation really well since this is the basic template we will be using to solve the rest of the problems.

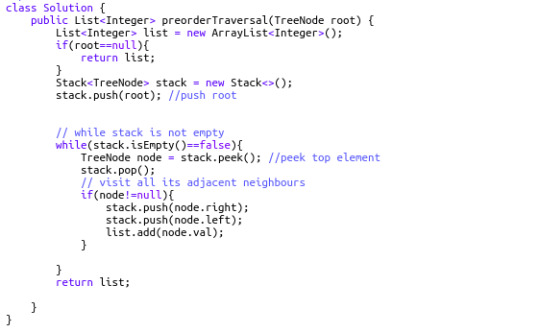
At first, we push the root node into the stack. While the stack is not empty, we pop it, and push its right and left child into the stack. As we pop the root node, we immediately put it into our result list. Thus, the first element in the result list is the root (hence the name, Pre-order). The next element to be popped from the stack will be the top element of the stack right now: the left child of root node. The process is continued in a similar manner until the whole graph has been traversed and all the node values of the binary tree enter into the resulting list.

145. Binary Tree Postorder Traversal (Difficulty: Hard)

Pre-order traversal is root-left-right, and post-order is right-left-root. This means post order traversal is exactly the reverse of pre-order traversal. So one solution that might come to mind right now is simply reversing the resulting array of pre-order traversal. But think about it – that would cost O(n) time complexity to reverse it. A smarter solution is to copy and paste the exact code of the pre-order traversal, but put the result at the top of the linked list (index 0) at each iteration. It takes constant time to add an element to the head of a linked list. Cool, right?

94. Binary Tree Inorder Traversal (Difficulty: Medium)

Our approach to solve this problem is similar to the previous problems. But here, we will visit everything on the left side of a node, print the node, and then visit everything on the right side of the node.

323. Number of Connected Components in an Undirected Graph (Difficulty: Medium)

Our approach here is to create a variable called ans that stores the number of connected components. First, we will initialize all vertices as unvisited. We will start from a node, and while carrying out DFS on that node (of course, using our magic spell), it will mark all the nodes connected to it as visited. The value of ans will be incremented by 1.

import java.util.ArrayList; import java.util.List; import java.util.Stack; public class NumberOfConnectedComponents { public static void main(String[] args){ int[][] edge = {{0,1}, {1,2},{3,4}}; int n = 5; System.out.println(connectedcount(n, edge)); } public static int connectedcount(int n, int[][] edges) { boolean[] visited = new boolean[n]; List[] adj = new List[n]; for(int i=0; i<adj.length; i++){ adj[i] = new ArrayList<Integer>(); } // create the adjacency list for(int[] e: edges){ int from = e[0]; int to = e[1]; adj[from].add(to); adj[to].add(from); } Stack<Integer> stack = new Stack<>(); int ans = 0; // ans = count of how many times DFS is carried out // this for loop through the entire graph for(int i = 0; i < n; i++){ // if a node is not visited if(!visited[i]){ ans++; //push it in the stack stack.push(i); while(!stack.empty()) { int current = stack.peek(); stack.pop(); //pop the node visited[current] = true; // mark the node as visited List<Integer> list1 = adj[current]; // push the connected components of the current node into stack for (int neighbours:list1) { if (!visited[neighbours]) { stack.push(neighbours); } } } } } return ans; } }

200. Number of Islands (Difficulty: Medium)

This falls under a general category of problems where we have to find the number of connected components, but the details are a bit tweaked. Instinctually, you might think that once we find a “1” we initiate a new component. We do a DFS from that cell in all 4 directions (up, down, right, left) and reach all 1’s connected to that cell. All these 1's connected to each other belong to the same group, and thus, our value of count is incremented by 1. We mark these cells of 1's as visited and move on to count other connected components.

547. Friend Circles (Difficulty: Medium)

This also follows the same concept as finding the number of connected components. In this question, we have an NxN matrix but only N friends in total. Edges are directly given via the cells so we have to traverse a row to get the neighbors for a specific "friend". Notice that here, we use the same stack pattern as our previous problems.

That's all for today! I hope this has helped you understand DFS better and that you have enjoyed the tutorial. Please recommend this post if you think it may be useful for someone else!

[johnwalker120]

using adjacency list undirected graph storage to achieve the breadth-first traversal.-–中英雙語句子 using adjacency list undirected graph storage to achieve the breadth-first traversal. 採用鄰接表儲存實現無向圖的廣度優先遍歷。 using adjacency list undirected graph storage to achieve the breadth-first traversal. 採用鄰接表儲存實現無向圖的廣度優先遍歷。

[programmingandengineering]

Algorithms (Sec: 102) Homework 4: Graph Algorithms: Part I

In this homework, we will focus our attention to searching on graphs and finding minimum span-ning trees. Problem 1: Graph Traversal 50 points Demonstrate both breadth-first search (BFS) and depth-first search (DFS) algorithms (with v1 as the start node) on the unweighted, undirected graph shown in Figure 1. Clearly show how each node-attribute (including frontier) changes in each iteration in…

[myprogrammingsolver]

HW4: Graphs, Traversals Solved

Q1. Given an undirected graph with 10 vertices but 45 edges, which of the following will be true? Select all that apply. Every node will have at least one neighbor The graph will have duplicate labels An Adjacency List would be more space-efficient to represent this graph vs. a Matrix The graph is GUARANTEED to have a cycle in it None of the above Q2. There are N cities, with M roads, where…

[felord]

CS112-Problem Set 11 Solved

CS112-Problem Set 11 Solved

Problem Set 11

Graphs: Representation, Traversal

Suppose a weighted undirected graph has n vertices and e The weights are all integers. Assume that the space needed to store an integer is the same as the space needed to store an object reference, both equal to one unit. What is the minimum value of efor which the adjacency matrix representation would require less space than the adjacency linked…

[sophyjsun-blog]

Some funny pickup lines wrote by CS dude (I’m dying)

I found these lines so genius and grew so eager to share this silly happiness with others, only to find I have no proper person to share this with. This is the pathetic moment when I realized how lonely I am. 

Excerpt from Larry Liu, originally posted on subtle asian dating:

“ I wrote some pick-up lines for all my Comp Sci majors out there: • Hey girl, are you a binary search tree? Because I'd like to insert some children inside of you • Hey girl, are you the agile software development paradigm? Because I wanna use you at the same time as six other people until we come to a collective finish • Hey girl, are you a bit-encoded binary signed integer? Because the two of us really complement each other • Hey girl, are we in the same instance of an object-oriented class? Because I'd like to access your privates • Hey girl, are you a mutex for Linux thread synchronization? Because I wanna put my key in your lock • Hey girl, are you a computer virus? Because you can put a Trojan on my hard drive any day • Hey girl, are you a recursive problem that doesn't require memoization? Because I'd like to divide your legs and conquer you • Hey girl, do you have a backdoor vulnerability? Because I'd like to do some penetration testing just to be safe • Hey girl, are you a string class in Java? Because my love for you is immutable • Hey girl, are you a binary search algorithm? Because you found my heart in O(log n) time • Hey girl, are you an undirected adjacency matrix graph? Because I wanna traverse your body in depth • Hey girl, are you a dynamically-sized unordered associative hash table? Because I wanna linearly probe you

“

[iitocw-blog]

Binary Heaps | Data Structure and Algorithms | IIT-OCW

Data Structures

Course objective: The objective of the course is to familiarize students with basic data structures and their use in fundamental algorithms.

Course contents: Introduction to object oriented programming through stacks, queues and linked lists. Dictionaries: skip-lists, hashing, analysis of collision resolution techniques. Trees, traversals, binary search trees, optimal and average BST’s. 2-4 trees and red-black trees. Tries and pattern matching. Priority queues and binary heaps. Sorting: merge, quick, radix, selection, heap. Graphs, Breadth first search and connected components. Depth first search in directed and undirected graphs and strongly connected components. Spanning trees: Prim's and Kruskal’s algorithm, union-find data structure. Dijkstra’s algorithm for shortest paths, shortest path tree. Directed acyclic graphs: topological sort and longest path.

Recommended Book (1) Introduction to Algorithms --Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein .