#countability and separation axioms

[the-least-undefinable-ordinal]

An effortpost about the Suslin Hypothesis

We all know and love the real numbers, they are a totally ordered set and most people graduate from high school understanding it's unbounded (i.e. has no greatest element and no least element) and dense (i.e. there is always a real number between any two different real numbers).

Some slightly less known facts about the real line: it's complete and separable (these are probably known by most people who study math in college).

The real line being complete means every bounded subset has a least upper bound (equivalently, every bounded increasing succession converges), note this property doesn't hold for the rational numbers, for example the set of all rational numbers smaller than the square root of 2 doesn't have a rational least upper bound (a fun little exercise is describing the aforementioned set without using irrational numbers).

Separable means it has a dense countable subset (one such set is the set of rational numbers), where countable means there is a one to one correspondence to the set of the natural numbers (also known as the counting numbers 1,2,3,...) and a subset A being dense means for any two distinct real numbers there is an element of A (it's another fun exercise to prove the rational numbers are indeed dense in the real numbers).

Now, Cantor proved that any totally ordered non-empty set X that is unbounded, dense, complete and separable must be order isomorphic to the real line, i.e. there is an order preserving one to one correspondence to the real line such that its inverse is also order preserving.

From the previous hypothesis we can deduce that any collection of pairwise disjoint open intervals is at most countable, the proof uses that we can take a rational number from each interval (since they're disjoint we don't risk taking the same one twice), so there can't be more intervals in this collection than rational numbers, but there are countably many rational, qed.

The condition "All collections of open intervals are at most countable" is known as the "countable chain condition" or ccc.

So, we know separable implies ccc, Suslin asked "What if we weakend the separable condition to the ccc?" i.e. are all totally ordered, unbounded, dense, complete sets with the ccc order isomporphic to the real line?

50 years later Solovay and Tennenbaum proved the anwser is "Who knows!", by which I mean there can be no proof from the axioms of ZFC of either the confirmation or refutation of the Suslin hypothesis.

Stay tuned for part two, where I introduce Aronszajn lines (the blorbo from my thesis), coming whenever I really need to procrastinate again!

[lilith-hazel-mathematics]

I'd like to add that there's a technical sense in which the result for determinants & polytopes is elementary, in that the result is captured by the power of Peano Arithmetic. So you for sure don't need the full power of measure theory. In particular it suffices to use the Peano-Jordan measure: the outer Jordan content of a compact set agrees exactly with the Lebesgue measure of that set. In any case, the Lebesgue outer measure is typically defined as follows.

The measure of a box is the product of its side lengths

A simple set is a countable disjoint union of boxes, and its measure is the sum of the measures of those boxes

The Lebesgue outer measure of a set is the infimum measure of any simple superset.

In the case of the Jordan measure, "countable union" is replaced by "finite union", but otherwise it's the same. It's a foundational theorem that the overlap in the above definitions is consistent: the infimum measure of the simple supersets of a box is exactly the product of that box's side lengths. Interestingly, to define measure, it suffices to only consider boxes & simple sets having rational coordinates. Critical to the Jordan measure however, there's only countably many simple sets having rational coordinates, since the Jordan measure only considers finite unions. Peano Arithmetic has no problem reasoning about finite lists of rational coordinates, and so the Jordan measure is definable over a conservative extension of Peano Arithmetic. For polytopes, they can be proved measurable using very elementary techniques, and in fact we won't need anything beyond the axioms of an ordered field. This is the sense in which the proof is elementary.

Okay, putting the technical stuff away, I'll just show you what the proof looks like.

-----

To fully prove the relationship between determinant and measure, it does suffice to handle the case of a box. If the matrix is diagonal, then the proof is trivial since the image of a box will be another box, and the measure of a box is easily computed. For a shear matrix transform, we partition our box into a large number of thin slices, thin along the dimension being sheared, and then approximate the image by similarly sized slices. As the width of those slices tends to zero, the measured approximation of the image will converge to the measure of the original box. This is satisfactory to us, since the determinant of the matrix for a shear is 1. Notice that that only required finite additivity and monotonicity, so the argument works for the Jordan measure. Finally, In the sense of elementary row operations, every invertible matrix can be expressed as a product between a diagonal matrix and a finite number of shear transforms. Consequently the claim extends to all invertible matrices by proxy of those simpler cases. For non-invertible matrices, we instead approximate the image by arbitrarily thin boxes to argue that the measure of the image will be zero. The claim is finally generalized to any measurable set by approximating it with simple sets.

The above proof doesn't require the comprehension axiom at all: the result holds for any set known to exist; which sets actually exist is a separate issue. It also doesn't need the completeness axiom either, for basically the same reason. The above result is proved for polytopes by demonstrating that they are actually measurable. First you'll want to show that the unit simplex is measurable, which is mostly demonstrated by partitioning the unit hypercube into a finite number of congruent simplices. Next, any arbitrary simplex is proved measurable as it's obtained from a linear transform of the unit simplex; the previous proof can be modified slightly to show that linear transforms preserve measurability. Lastly, each polytope can be partitioned into a finite number of simplices using a triangulation, from which we infer that every polytope is measurable.

Am I correct in assuming that if you want to rigorously derive formulas for calculating volumes of arbitrary n-dimensional polytopes (or to even formally define what a volume is in the first place) you need to get into measure theory? Or is there a simpler, more algebraic way that still leads to a fully formal and rigorous proof?

(I'm specifically interested in a rigorous proof that the correspondence between determinants of n x n matrices and volumes of n-parallelotopes spanned by the corresponding vectors continues to hold for arbitrary n)

[noctumsolis]

According to Lee Smolin, the eight stages by which mathematics develop from the study of relations among natural objects are as follows:

1. Exploration of the natural case (e.g., countable objects, 3D spatial geometry, etc.)

2. Formalization of natural knowledge (e.g., arithmetic, trigonometry)

3. Exploration of the formalized natural case.

4. Evocation and study of variations on the natural case (e.g., non-euclidean geometry)

5. Invention of new modes of reasoning (e.g., axioms)

6. Unification of cases within more general frameworks (e.g., Riemannian geometry)

7. Discovery of relationships between constructions generated autonomously within mathematics

8. Discovery of the applicability of nature of knowledge developed internally.

Smolin rejects the idea that the study of mathematics constitutes the exploration of a Platonic realm separate from physical reality. Rather, he thinks that it represents an evocation from reasoning about items in the natural world. Thus, its applicability to physics occurs precisely because it is, historically, rooted in reasoning about the physical universe.

I need to learn more about this. So far it makes perfect sense!

[coursesforallacademynoida]

B.Sc Tuition In Noida For Topology

B.Sc Tuition In Noida For Topology

B.Sc Tuition In Noida For Topology

CFA Academy For B.Sc Maths Tuition Classes In Noida. Linear Algebra Tuition In Noida, Calculus Tuition In Noida, Real Analysis Tuition In Noida, Complex Analysis Tuition In Noida, Ordinary Differential Equations Tuition In Noida, Algebra Tuition In Noida, Functional Analysis Tuition In Noida, Numerical Analysis Tuition In Noida, Partial Differential Equation…

[jonathankatwhatever]

Find myself going over my character design, seeing how the justifications actually do fit the storyline. Trying to figure out a movement reason, a line segment reason, for this form of structure, and there it is in front of me.

I ran through a version earlier, that this loops around the complexity of a choice. So back when, I drew out gender and attractions and various triangles, and said I had to pursue this branching. Full acceptance of the identification in that branching brought this loop to the same point, but with a difference arranged over concepts like collaboration. That additional conceptual layer segments, which means it is clipped x,yK. This allows a lot of movement because each suboutcome contained in collaboration orders, so the choice is not pure binary.

This is fulfilling something I’ve been experiencing but have been unable to type: the awareness of how little I know has shifted. So I just had a version of you come through that embodied the version in which this is coincident, but with awareness that it is not coincident, which means it embodied a contradiction. It is the reflection of I know everything. That is true dimensionally, because dimensionally means the experiences are both recoverable and generable by the carving out of countable perspectives through the related inversions of grid squares. So I recognize dimensions I know nothing about: they are countable areas of some expertise or interest I do not have. I have always seen the dimensionality in things, but now I’m able to analyze that.

To me, ‘choice’ is an axiom that flows from the statement that any set exists in a measure of its potential so that potential enables ordering up to the limit of that potential. This becomes the cross-inversion of grid squares. So something like there is a Potential P, which is uncountable, and out of it are defined segments countable to definable lengths, points, etc., so it is not that cP for countable P sums to P but that specified exists within the unspecified. In grid squares, this become obvious: you are always carving out a space for actions. It is the iterative count to a point where iterative counts indicate a triangle and a square. That is, these ideal relationships exist in the complex field of all the ways they could not be.

So, big question: why do it to the max? To the limit? To where resources conflict with harm inflicted, all to impose a hard limit. Why Isaac? One message is ‘I want devotion that is not self-harming.’ That kind of clarity is the limit, like twirling on your toes requires the complexity to resolves as you rotate to keep you rotating. In this case, the entire project has been about defining eternity and the connection of individuals and groups to it.

That eternity consists of the complexity connected to you, which of course connects you to groups. And this is mirrored on the inside: the complex being inside you is dimensional in the same way as any other GS contains dimensions.

I think this may be an example: a chest on antiques roadshow has a history, so that is a 3D object which has gone through a bunch of complexity over time. Attached to that chest, and affecting how it has been treated, are values. These values may also have changed over time, perhaps reflecting how the chest became more of a relic. What is the dimension of the price? So attached to the chest is a stack of abstract money. This stack generally represents conceptions of worth. So there is a process at work which represents the combinations of threads of valuation, some of which may be separate from external valuation. The adjustment of one 4D object on another is what grid squares treats as D5: it tugs or otherwise adjusts a D4 object. D6 is harder.

This allows abstract attachment like of pretend dollars. And that gets to something I only recently remembered; the rubber ducky transition. It was actually a toy boat, but one day I was in the bath and it was just a toy boat. I no longer would splash with it as if it were more, because the realism had moved inside my head and did not need the object. This came to me in thinking about how cats play with objects. So for a cat, listening for a mouse carries with it the satisfactions of mouse hunting. That is the spline sticking out through the experience: the stimulations arrange across the space, which arranges them on the line (over complexity), and that is why a cat often takes a long time to learn how to kill. My assumption is the hesitation is connected to weaning and motherly instruction turning that on, so the juvenile behavior stutters.

This arranges the quadrant and the quadrant into the unit circle seamlessly. It’s actually astonishing. That is, you count out on x,yK and that clips to the E and the enclosing countable infinities that are in the inversive relationship!!!

[jmarsreb-blog]

Topology (pt. 1)

Let $X$ be a set. We call the a subset of the powerset $T_X \subseteq \mathcal{P}(X)$ a topology if it satisfies three axioms;

(1) $X, \emptyset \in T_X$,

(2) $T_X$ is closed under arbitrary unions; that is, if $\{E_\alpha\}$ is a collection of sets such that $E_\alpha \in T_X$ for all $\alpha$, and $\alpha$ could be an uncountable collection, then $\bigcup_\alpha E_\alpha \in T_X$,

(3) $T_X$ is closed under countable intersections; that is, if $\{E_\alpha\}$ is a collection of at most countably many sets where the $E_\alpha \in T_X$, then $\bigcap_\alpha E_\alpha \in T_X$.

The sets which are in $T_X$ are called open sets. If $E \subset T_X$ such that $E^C \in T_X$, we call $E$ a closed set.

Remark: Open and closed are not mutually exclusive terms. We can have sets which are both open and closed; for example $X$ is open, since $X \in T_X$, while $X$ is closed since $X^C = \emptyset \in T_X$.

Remark: To be precise, we should write $(X, T_X)$ as a tuple which denotes a set $X$ and it’s topology. However, in general, the topology is understood from context, so we drop it when talking about $X$.

What topologies do is they classify continuous functions. That is, if $X$ and $Y$ are topological spaces (spaces equipped with topolgies denoted $T_X$ and $T_Y$ respectively), then a function $f : X \rightarrow Y$ is continuous if, for all $E \in T_Y$, we have $f^{-1}(E) \in T_X$. This matches our definition of continuous in the $\mathbb{R}$ sense (that is, the epsilon-delta sense) while also generalizing it to abstract spaces.A function $f : X \rightarrow Y$ is called a homeomorphism if $f$ is bijective, continuous, and $f^{-1}$ is also continuous. If there exists a homeomorphism between two topological spaces, we call those spaces homeomorphic.

Remark: Much like a bijection between sets means that the sets are essentially the same and an isomorphism between groups means that they are the same, a homeomorphism acts as a way of saying two topological spaces are essentially the same.

Example: One example of a topology is $\mathcal{P}(X)$ itself; this is called the discrete topology.

Example: Another example of a topology is the trivial topology, which consists of just $X$ and $\emptyset$.Example: Let $B_r(X) = \{y \in \mathbb{R} \ : \ |x-y| < r\}$. This is sometimes referred to as the ball of radius r centered at x. We say that a set $U$ is open in $\mathbb{R}$ if, for all $x \in U$, we have that there is an $\epsilon > 0$ so that $B_\epsilon(x) \subseteq U$. Notice that $B_r(X)$ itself is an open set; it is also sometimes referred to as the open ball of radius r centered at x for this reason.

In the example, we had that these balls somehow generated the topological space. We expand on this now; we say that a collection of sets $\{B_\alpha\}$ form a base for a topological space $X$ with topology $T_X$ if, for all $U \in T_X$ we have $U = \bigcup_\alpha B_\alpha$. That is, we can write every open set as a union of the basis elements. Here, the basis elements are the open balls, since denoting the necessary $\epsilon >0$ for each $x$ by $\epsilon_x$, we have $U = \bigcup_{x \in U} B_{\epsilon_x}(x)$.

Let $X$ be a topological space, and $x \in X$ a point. We call a subset $V \subseteq X$ a neighborhood of x if there is an open set $U$ such that $x \in U \subseteq V$. If $S$ is a collection of points, we have that $V$ is a neighborhood of S if, for all $x \in S$, we have that there is an open set $U$ so that $x \in U \subseteq V$. That is, $V$ is a neighborhood of all the points $x \in S$.

We call a topological space Hausdorff if it satisfies the following: for all $x, y \in X$, $x \neq y$, there are neighborhood $V_x, V_y$ of $x$ and $y$ respectively so that $V_x \cap V_y = \emptyset$. In a sense, this is saying that we can find neighborhoods which are separate from each point.

Remark: If there are neighborhoods which satisfy this, then in particular there are open neighborhoods which satisfy this.

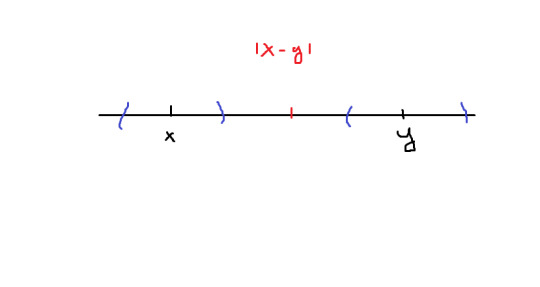
Example: One example of a Hausdorff space is $\mathbb{R}$; take $x \neq y \in \mathbb{R}$. Let $r = |x-y|/4$. Then we have $x \in B_{r}(x)$, $y \in B_{r}(y)$. Let $z \in B_r(x) \cap B_r(y)$. Then we have $|x-z| < |x-y|/4$ and $|y-z| < |x-y|/4$. By the triangle inequality, we get $|x-y| < |x-z| + |y-z| < |x-y|/2$; but this is a contradiction if $|x-y| \neq 0$. Hence, $B_r(x) \cap B_r(y) = \emptyset$. We can visually see this contradiction below;

Non-Example: Let $X$ be an uncountable set; for example, $\mathbb{R}$. Let $T_X$ be the cofinite topology; that is, the collection of sets $U \subseteq X$ such that $X^C$ is at most countable, and throw in $\emptyset$. Then we can quickly see that $T_X$ is a topology;

(1) $X \in T_X$, since $X^C = \emptyset$, and $\emptyset \in T_X$ since we threw it in.

(2) Take an arbitrary collection of sets in $T_X$, denoted by $\{E_\alpha\}$. Then DeMorgan’s laws say that (after throwing at all the null-sets, which aren’t contributing anything) $\left(\bigcup_\alpha E_\alpha\right)^C = \bigcap_\alpha E_\alpha^C \subseteq E_{\alpha_0}^C$ for some $\alpha_0$ in the indices, which is countable and so this is countable. Hence, the arbitrary union is in $T_X$.

(3) If $\{E_\alpha\}$ is an at most countable collection of sets in $T_X$, none of which are the null-set since that makes this trivial, then DeMorgans tells us $\left( \bigcap_\alpha E_\alpha\right)^C = \bigcup_\alpha E_\alpha^C$ is a countable union of countable things, and so countable.So this is indeed a topology. However, take $x \neq y \in X$, and take any neighborhoods $V_x, V_y$. We have there are open sets $x \in U_x \subseteq V_x$, $y \in U_y \subseteq V_y$, and we must have $U_x \cap U_y \neq \emptyset$. Assuming otherwise, then we have that DeMorgan’s tells us $U_x^C \cup U_y^C = X$, which is impossible since $X$ is uncountable and these are countable sets. Therefore, $V_x \cap V_y \neq \emptyset$.

We can also think about general sets in $X$ and their relation to open and closed subsets. The interior of a subset is the largest open subset contained in it, while the closure of a subset is the smallest closed set containing it. Going back to neighborhoods, then, $V_x$ is a neighborhood of $x$ if $x$ is in the interior of $V_x$, denoted by $\text{Int}(V_x)$.

Another important concept when studying topological spaces is the concept of compacity. A cover of a topological space $X$ is a collection of sets $\{E_\alpha\}$ such that $X \subseteq \bigcup_\alpha E_\alpha$. An open cover is a cover in which all of the sets are open. A refinement of a cover is a subcollection $\{E_{\alpha_i}\}$ such that $X \subseteq \bigcup_i E_{\alpha_i}$. A topological space is then said to be compact if every open cover admits a finite refinement. A subset $\emptyset \neq Y \subseteq X$, where $X$ is a topological space, admits something called the subspace topology, which is the induced topology $T_Y = \{U \cap Y \ : \ U \in T_X\}$. That is, take all of the open sets in $X$ and intersect them with $Y$.

A subset $Y \subseteq X$ is said to be compact in terms of it’s subspace topology.

Remark: This is equivalent to just saying that if there is an open cover of the subset, it admits a finite refinement. That is, we don’t necessarily have to jump down to the subspace topology.

Remark: Let $X$ be a topological space, $U \subseteq X$. To show that $U$ is open, it suffices to show that for every $x \in U$, there is an open subset $U_x \subseteq U$. This is because $\bigcup_{x \in U} U_x = U$, and an arbitrary union of open sets is still open.

Remark: In a Hausdorff space, a compact set is closed. To see this, let $H \subseteq X$ be compact. For $H$ to be closed, $H^C = X - H$ has to be open. We use the trick above. Fix $y \in X-H$. For all $x \in H$, we have that there are $U_x, V_x$ so that $x \in U_x$, $y \in V_x$, $U_x \cap V_x = \emptyset$. Let these $U_x, V_x$ be open. Then we have that $\bigcup_{x \in H} U_x$ is an open cover of $H$, and so by compactness we get that there is a finite refinement $\bigcup_{i=1}^k U_{x_i}$. Examine $\bigcap_{i=1}^k V_{x_i} \subseteq X-H$, since none of these meet any of the $U_{x_i}$ which contain $H$. Then since we have a finite intersection of open sets, it’s still open, and furthermore $y \in V_{x_i}$ for all $i$. Hence, $X-H$ is open by the prior remark, so $H$ is closed.

[wumblr]

the relevant term, unfortunately, is "haecceitism," which describes perspectives on "the identity of the indiscernibles."

if it is possible to build two identical diamonds, and if these are then the same object -- that's a haecceistic interpretation. if it's impossible to build two identical diamonds, or if they can be built but remain distinguishable as separate objects -- that's anti-haecceist. this is unrelated to whether they are entangled (unless is it specifically the entanglement that endows them with haecceistic properties, i.e. an entangled diamond pair is haecceistic and an unentangled but merely atomically identical pair is anti-haecceist)

things that are qualitatively indiscernible cannot be quantized (i think this is how one-electron theory occurred to john wheeler), and in order to be adequately described, they require a branch of mathematics where quantities are not exclusively continuous or discrete, and infinities are safely excluded. (probably topos theory, but i don't think it's axiomatically finite)

i'm not the only person saying this -- john baez and cohl furey seem to have come to the same conclusions starting from more philosophical and mathematical arguments, and achim kempf uses radio signal sampling metaphors to describe physical observables as simultaneously discrete and continuous within an operationalist perspective. (and me? i've just been throwing spaghetti against the wall until some of it sticks)

anyway, the questions above still very much interest me, about haecceistic vs anti-haecceistic objects as they cross causal horizons, the relationship between haecceism and entanglement (if any), the theoretical and operational differences between distinguishable black holes vs. indiscernible ones, and the implications for a theory with symmetry of numerosity (i.e. collapsible, mutable quantities due to many indiscernibles, and the limited arithmetic available therein)

i'm not sure, but i think excluding infinities prevents a problem i previously posted, where in order to define a number system that is neither (or both) discrete and/or continuous, you need a cardinality between countable and uncountable infinities, which cantor assumed was impossible, and godel later supplied a proof within accepted theory... so uh, quantitative symmetry and "discrinuous" counting are believed to be proven impossible because the proof used a system logic that excludes them lol

godel's triumph was pointing out that every system of logic excludes something. i think the ideas i'm suggesting are necessarily subject to the same obstacle, unless it can be proven that godel's incompleteness theorem doesn't work under different axioms lmao

i have two diamonds, unbreakable and entangled, in a 1:1 correspondence such that their structure is atomically identical, and each atom is entangled to the particle in the exact same location in the opposite diamond. if i throw one into a black hole, and make precise measurements on the other, what would i observe?

[mathematicianadda]

(Long) Detailed Proof of Kőnig's Lemma (Explicit, Down to Axiom of Choice)

Kőnig's Lemma states that in an infinite, locally finite, connected graph $G$, there exists an infinite one-way path (a ray). The proof of it in my graph theory book (Introduction to Graph Theory, 4th ed., Wilson) had a sour taste to it, like it was covering something up. So I checked out proofs from other sources, which also seemed to cover up something which felt very close to the foundation (i.e. using the axioms). After looking it up I found out that this is indeed the case, as it results directly from the axiom of dependent choice (DC).

This wasn't a question on an assignment for me or anything, but I wanted to try to give a more detailed, albeit lengthy proof of the lemma with more explicit constructions and play-by-play, highlighting some of the key points and bare bones math going on here (including the general statement of the lemma and the use of DC), to the best of my understanding. I was hoping that anyone with time to spare hands could review or give comment, make sure everything I'm stating things correctly! And of course, I would be happy if this helps anyone in a similar predicament that comes to read this in the future, or helps anyone to appreciate the deeper levels of a simple theorem.

I've enabled the "answer your own question" box so I can post my proof separately, but I encourage/challenge others to do the same and make a detailed construction as an exercise, especially during these times of isolation!

Below I'll prove a similar theorem which uses Kőnig's Lemma in a more general form (but sweeps DC under the rug). It's a good reference because it's easier to understand without a super explicit construction:

Let $G$ be a countable graph such that every finite subgraph of $G$ is $k$-colourable. Then $G$ is $k$-colourable.

Proof

Since $G$ is countable, its vertices are enumerable as $v_1$, $v_2$, $v_3$, etc. Let $G_n$ be the (finite) subgraph induced by vertices $v_0$ through $v_n$. Since each vertex $v_n$ corresponds to a finite induced subgraph $G_n$, there are countably many $G_n$. Since $G_n \subset G_{n+1}$ for all $n$ by construction, the union over all $G_n$ yields $G$. Since each $G_n$ is finite, there are countably many corresponding sets $C_n$ of valid $k$-colourings of $G_n$, each non-empty with a finite number of elements given by the chromatic polynomial of $G_n$, $P_{G_n}(k)$. If we consider a colouring of $G_{n+1}$ and remove vertex $v_{n+1}$, we are left with a valid colouring of $G_n$: removing vertices does not invalidate a colouring. And so this valid colouring of $G_n$ must be an element of $C_n$. In general, for every colouring $c_{n+1} \in C_{n+1}$ of $G_{n+1}$ there is some colouring $c_{ind} \in C_{n}$ such that $c_{ind} \prec c_{n+1}$ (i.e. $c_{ind}$ is induced on $G_n$ by $c_{n+1}$). Kőnig's Lemma states that since there are countably many non-empty $C_n$ that follow these conditions, we must have a countable set of $c_n \in C_n$ such that $c_n \prec c_{n+1}$ for all $n$. If there were not, then all inductive sequences of colourings would terminate at some finite point $t$. If we take $\tau$ to be the maximum such $t$ over all sequences, then $C_{\tau + 1}$ must be empty, contradictory to our assumption that all $G_n$ are $k$-colourable (and in turn that all $C_n$ are non-empty). Therefore there is a countable set of inductive valid $k$-colourings $c_n$, and their union gives us a valid $k$-colouring of $G$.

Thus, $G$ is $k$-colourable. $\blacksquare$

The general form of Kőnig's Lemma can be stated as follows (paraphrasing Infinite Graphs - A Survey, by Nash-Williams, 1967):

Given a countable sequence of finite, non-empty, disjoint sets $S_n$ and a relation $\prec$ on $\bigcup S_n$, if for each element $s_{n+1} \in S_{n+1}$ there exists an $s_n \in S_n$ such that $s_n \prec s_{n+1}$, then there exists a countable sequence of elements $(s_n)$ such that $s_n \prec s_{n+1}$ for all $n$.

The end of the $k$-colouring proof I gave is basically the proof of this theorem. In this general form, the $S_n$ can be thought of as "configuration spaces" (finite sets of valid configurations), and the relation $\prec$ can be thought of as an inductive consistency relation. In the $k$-colouring proof, our configuration spaces are the $C_n$ and they are finite due to the chromatic polynomial of $G_n$, though I didn't explicitly construct them so we can't show that they are disjoint. But as I mentioned, this is still easier to understand without explicit construction. This is because we iterate out $G$ vertex by vertex, and as a result, we get a natural correspondence between the iterated subgraphs and their colourings. In proving the graph theoretic result about the existence of an infinite one-way path, the iteration scheme is not vertex by vertex, and so more explicit construction is needed to make the simple argument as above. That will be in my proof below, and similar methods can be used to construct a more explicit proof of this $k$-colourability result, and one for planarity as well!

from Hot Weekly Questions - Mathematics Stack Exchange from Blogger https://ift.tt/34nujYj

[drunk-math]

A quickie, only because I haven't written anything since my "alloposium."

So I've been working on a post for a while that has to do with the metamathematical/philosophical concept of finitism, i.e., that the notion expressed by Russel's paradox, which he expressed as the barber's paradox (which can't be solved by saying the barber was a woman, or maybe it can, but more on that later), should be solved, rather than by the axiom of regularity, by an axiom of finitism, where infinite sets are treated as proper classes.  I'm rather dragging my feet on that, since maybe it turns out that trying to do math drunk is almost as foolish an endeavor as doing it sober.  Consider the Achaemenids, blah blah blah.

Meanwhile, I have to write something, so how about I excerpt the rant on the Banach-Tarski paradox I was going to put in, since it's pretty random anyway?

Now, you probably know the name Tarski from the Banach-Tarski paradox, that you can chop a sphere into a finite number of pieces (nine) and reassemble them into two spheres, which I’m now going to explain in tiresome, prosaic detail for really no reason at all.  First accept the axiom of choice, in the form that given a set of disjoint sets, you can infer the existence of a set containing exactly one member of each.  Now draw two axes through a ball at a funny angle - pretty sure one radian will do - anything that leaves no finite, alternating string of half-turns around one axis and third-turns (in either direction) around the other that ends up get you back to where you started.  (I think one radian will work because its sine and cosine are transcendental - this I’m sure of - and they’d have to be the solutions to a finite polynomial of algebraic coefficients to fail this criterion - this I’m also fairly sure of but can’t be arsed to work out.)  This guarantees that every such string corresponds to a unique rotation, and it’s easy to see that you can invert them by just going backwards (thus failing to alternate, I’m sure I don’t need to say).  Now, first, let’s split the surface of the sphere into four sets - the fourth will be all the points that don’t move in one of these rotations, and you’ll see why I’m calling it the fourth very shortly.  In fact, by the end of this sentence: every point belongs to what’s known as an “orbit” of all the points you can get to by a rotation in the set of rotations described above, which is a set since the relation is reflexive (the trivial rotation - zero degrees - is in the set), symmetric (the inverse of every rotation in the set is in the set), and transitive (the composition of two rotations in the set is in the set), which for every point not in the aforementioned fourth set (i.e., those not fixed in any rotation; note that the orbits of those in the fourth set will be entirely within the fourth set - in fact, I think but can’t prove the fourth set itself - if it were finite, it’d follow from the bijection, so stay tuned - since the operation of bringing it to the fixed point, giving it an appropriate turn, and bringing it back will keep it fixed while being a nontrivial element the set of rotations) has a bijection to the set of rotations, and having CHOSEN (would that I could figure out how to add sparkles to that) one from each orbit you get a set that itself has an orbit that’s the whole sphere bar that fourth set, and that orbit we’ll divide into three unions of elements of the orbit by separating the rotations into three sets.  Yes, I will call that a sentence, thank you very much.  Anyway, the rotations, the trivial rotation is in the first set, if you turn a rotation around the third-turn axis in one direction it goes from the first to the second to the third and back, the other it goes from the third to the second to the first and back, regardless of whether the instructions alternate or not.  Likewise, if you flip a rotation in the second or third set, you get one in the first set, always.  However - if you flip one in the first set, it depends.  Remembering that each rotation has a unique alternating representation of flips and turns (let’s call ‘em that because why not?), if the last instruction in that representation is a flip, you obviously go back to whichever brought you here.  If it’s a turn, you go to the second.  So now you take these four sets on the surface and use them to divide the sphere into four sets plus the center.  First, take the second and third away.  Now, you can flip the first set to get the second and third, break it up, turn both parts to get two copies of the first, and flip one to get the second and third again.  Since that’s keeping the fourth and the center, you’ve now got the whole ball plus a nice chunk of it.  (If you’re keeping score, only four pieces - the one corresponding to the fourth set and center, one for the preimage of each of the second and third sets under the mapping from the first - have actually been rearranged separately, and one for the points beneath the second and third sets themselves.  Only the lattermost will be considered from here on out.)  The next part’s tricky, inasmuch as it involves a hypothetical ball and its hypothetical rearrangement into a subset of the other two sets, but that’s not going to be what we’re doing in the end: to wit, hypothetically rearrange the hypothetical ball in the reverse of the way we build the last ball to get just the points under the first and fourth sets (and the center), then turn the first set to become the second, turn the fourth to be entirely in the other three (since the set of rotations we built was countable, the points of the fourth set on the sphere - i.e., the surface - are countable, and since only two rotations can connect a given two and there are uncountably many rotations since there are uncountably many angles, there being are uncountably many reals between zero and tau, there must be such a rotation) and just like the entirety of the three sets before break it in two and rotate it totally into the third set, and shift the center to be somewhere else, anywhere else, in the third set (“chosen,” which didn’t actually make my phrasing, but pretend it did, gets no sparkles because it’s only one arbitrary choice, not infinite - more on that nasty little-big word soon).  The next bit to break off is the points under the second and third sets of the sphere that you’ll never get to by doing this to the points outside the second and third, or to the points you get from doing that, or from doing that, ad inf.  (Arguably a different sense, but really also sort of the same - Euclid’s sense, to the extent he had one.)  These stay put, while the points that you will get you break into five according to where you get them, and send them there.  Since each iteration is walked back one, you end up with another entire ball.  So now, like the barber, you’ve got two balls.

(The "you probably know the name Tarski..." thing comes from a reference to Tarski-finiteness, which is the property that any chain of subsets, i.e., set of subsets in which of any two one contains the other, has an element that contains all others, which without the axiom of choice doesn't necessarily imply finiteness, unless you assume it for all objects in the domain of discourse.)

Anyway, slightly simpler: Vitali sets.  So consider measure: if you have a finite number of disjoint intervals, the amalgamation has a "length" equal to their sum.  If you have a sequence of lengths of disjoint intervals that converges (e.g., 1 to 1.5, 2 to 2.25, 3 to 3.125, &c.), that'll converge to the sum, and if you have such a sequence that diverges, we'll say that's infinite, like the real line itself.  So let's consider just between zero and one, and divide up the numbers such that in each set, the difference between any two is rational.  Now, every such set will be of measure zero, but there are "too many" to put into a sequence, to that's fine.  Now let's CHOOSE one from every such set, and since they're disjoint, if you add a rational number, you'll get a different set that'll have the same measure, and if you take the part that's greater than one or less than zero, you'll get two disjoint sets whose sum has the same measure, and moving one will give you a set of the same measure between zero and one.  These can be put into a sequence, since the rationals can be, and they take up the whole interval, and since they're disjoint, they add up to the whole interval, but since they have the same measure, that's impossible, so they have no measure, not even zero.  The aliens who don't understand Euclidean geometry might have a different notion of "number," and in particular "infinitesimal" from us, but that would take more explanation, which I don't have on me.

So... as Izzard would say... yeah.

[dnsiaody]

CSIR UGC NET Application 2017

COMMON SYLLABUS FOR PART ‘B’ PLUS ‘C’ MATHEMATICAL SCIENCES DEVICE - 1 Analysis: Primary set theory, finite, countable and uncountable sets, True number system as the complete ordered field, Archimedean property, supremum, infimum. admission.scholarshipbag.com Sequences and series, convergence, limsup, liminf. Bolzano Weierstrass theorem, Heine Borel theorem. Continuity, uniform continuity, differentiability, indicate value theorem. Sequences plus a number of functions, homogeneous convergence. Riemann sums plus Riemann integral, Improper Integrals. Monotonic functions, types associated with discontinuity, functions of bounded variation, Lebesgue measure, Lebesgue integral. Functions of various variables, directional derivative, partially derivative, derivative as being a geradlinig transformation, inverse and implied function theorems. Metric areas, compactness, connectedness. Normed geradlinig Spaces. Spaces of constant functions as examples. Geradlinig Algebra: Vector spaces, subspaces, linear dependence, basis, aspect, algebra of linear changes. Algebra of matrices, position and determinant of matrices, linear equations. Eigenvalues plus eigenvectors, Cayley-Hamilton theorem. Matrix representation of linear changes. Change of basis, canonical forms, diagonal forms, triangular forms, Jordan forms. Internal product spaces, orthonormal base. Quadratic forms, reduction plus classification of quadratic types UNIT - two Complicated Analysis: Algebra of complicated numbers, the complex aircraft, polynomials, power series, transcendental functions such as rapid, trigonometric and hyperbolic features. Analytic functions, Cauchy-Riemann equations. Contour integral, Cauchy’s theorem, Cauchy’s integral formula, Liouville’s theorem, Maximum modulus rule, Schwarz lemma, Open umschlüsselung theorem. Taylor series, Laurent series, calculus of residues. Conformal mappings, Mobius changes. Algebra: Permutations, combinations, pigeon-hole principle, inclusion-exclusion principle, derangements. Fundamental theorem of math, divisibility in Z, congruences, Chinese Remainder Theorem, Euler’s Ø- function, primitive origins. Groups, subgroups, normal subgroups, quotient groups, homomorphisms, cyclic groups, permutation groups, Cayley’s theorem, class equations, Sylow theorems. Rings, ideals, excellent and maximal ideals, quotient rings, unique factorization site, principal ideal domain, Euclidean domain. Polynomial rings plus irreducibility criteria. Fields, limited fields, field extensions, Galois Theory. Topology: basis, thick sets, subspace and item topology, separation axioms, connectedness and compactness. UNIT -- 3 Ordinary Differential Equations (ODEs): Existence and originality of solutions of preliminary value problems for initial order ordinary differential equations, singular solutions of initial order ODEs, a system associated with first order ODEs. The common theory of homogenous plus nonhomogeneous linear ODEs, deviation of parameters, Sturm-Liouville border value problem, Green’s functionality. Partial Differential Equations (PDEs): Lagrange and Charpit strategies for solving first purchase PDEs, Cauchy problem intended for first order PDEs. Category of second order PDEs, General solution of increased order PDEs with continuous coefficients, Method of splitting up of variables for Laplace, Heat and Wave equations. Numerical Analysis: Numerical options of algebraic equations, Technique of iteration and Newton-Raphson method, Rate of convergence, Solution of systems associated with linear algebraic equations making use of Gauss elimination and Gauss-Seidel methods, Finite differences, Lagrange, Hermite and spline interpolation, Numerical differentiation and incorporation, Numerical solutions of ODEs using Picard, Euler, customised Euler andRunge-Kutta methods. Calculus of Variations: A variety associated with a functional, Euler-Lagrange formula, Necessary and sufficient situations for extreme. Variational strategies for boundary value troubles in ordinary and partially differential equations. Linear Essential Equations: The Linear integral formula of the first plus second kind of Fredholm and Volterra type, Options with separable kernels. Feature numbers and eigenfunctions, resolvent kernel. Classical Mechanics: General coordinates, Lagrange’s equations, Hamilton’s canonical equations, Hamilton’s rule and the principle of minimum action, Two-dimensional motion associated with rigid bodies, Euler’s dynamical equations for the movement of the rigid entire body about an axis, the concept of small oscillations. DEVICE - four Descriptive figures, exploratory data analysis Example space, discrete probability, 3rd party events, Bayes theorem. Unique variables and distribution features (univariate and multivariate); requirement and moments. Independent unique variables, marginal and conditional distributions. Characteristic functions. Possibility inequalities (Tchebyshef, Markov, Jensen). Modes of convergence weakened and strong laws associated with large numbers, Central Restrict theorems (i. i. g. case). Markov chains along with finite and countable condition space, classification of claims, limiting behaviour of n-step transition probabilities, stationary submission, Poisson and birth-and-death procedures. Standard discrete and constant univariate distributions. sampling distributions, standard errors and asymptotic distributions, distribution of purchase statistics and range. Strategies of estimation, properties associated with estimators, confidence intervals. Testing of hypotheses: most effective and uniformly most effective tests, likelihood ratio testing. Analysis of discrete information and chi-square test associated with goodness of fit. Big sample tests. Simple non-parametric tests for just one particular and two sample troubles, rank correlation and check for independence. Elementary Bayesian inference. Gauss-Markov models, estimability of parameters, best geradlinig unbiased estimators, confidence times, tests for linear ideas. Analysis of variance plus covariance. Fixed, random plus mixed effects models. Assured multiple linear regression. Primary regression diagnostics. Logistic regression. Multivariate normal distribution, Wishart distribution and their qualities. Distribution of quadratic types. Inference for parameters, partially and multiple correlation coefficients and related tests. Information reduction techniques: Principle element analysis, Discriminant analysis, Bunch analysis, Canonical correlation. Easy random sampling, stratified sample and systematic sampling. Possibility proportional to size sample. Ratio and regression strategies. Completely randomised designs, randomised block designs and Latin-square designs. Connectedness and orthogonality of block designs, BIBD. 2K factorial experiments: confounding and construction. Hazard functionality and failure rates, censoring and life testing, collection and parallel systems. Geradlinig programming problem, simple strategies, duality. Elementary queuing plus inventory models. Steady-state options of Markovian queuing versions: M/M/1, M/M/1 with restricted waiting space, M/M/C, M/M/C with the limited waiting area, M/G/1. All students are usually required to answer queries from Unit I. College students in mathematics are anticipated to answer an additional query from Unit II plus III. Students with within statistics are required in order to answer the additional question through Unit IV.

[jonathankatwhatever]

I had a series of understandings this morning, but they’re now jumbled because I barely slept. Example: I could categorize sexual couplings by equivalencies and symmetries. So for example, m-f can rotate to oral as an extension of kissing - which I dont think f-F do like they could and should, which I’m trying to express as a consequence of the gender across relationship with m-M, not as a judgement. I could have said m-M dont kiss well, but that’s an extrapolation, not something I’ve tested.

So for example, there are pairings, and these can expand to triangles which dont fully close. Like a guy divided in two, serviced bottom, by a girl, joined top in a kiss. That turns the communication across into an alternating flow: blow one, information flows up and down that guy across to other, who can then be serviced by hand or another mouth if you want complications. A double penetration is different because equal involvement requires a shift of position, either of the guys or of the girl. That makes 4 positions because the communication in each involves different ends of her with different degrees of freedom.

A gangbang is like a carousel in which focus shifts discretely within the blur of over-stimulus. Until it loses focus. That’s the appeal.

Took a short break, thought about how Harkness was daughter-in-law to the builder of Harkness Hall. I loved that place. My friend Patti was trying out to be a carilloneur, and the practice carillon was only available at odd hours. I escorted her a few times. Her banging on the wooden handles. Checking out the bells. It’s the only actual gothic stone, not steel structure at Yale. FLWright said he wanted to live in it so he wouldnt have to look at it. Put downs used to have art. And her bitch pack in St. Louis. I stopped at Kennedy + knowing that’s the best part of the coast. Never thought about the threads in the house and grounds.

Forms of grounds. Shades of brown.

I realized my male friends are hard m outside, fit and often muscular, but on the trans scale inside, though they dont seem aware of it. That can flip same or reverse, out and in. The number of twists possible gets large fast: awareness has a radiative quality. Should have been obvious: awareness defines by what it is not aware of because any awareness is separate to some extent, and that separateness is like the way the negatives sneak into my head. That’s a function of various separation axioms, which are now arise mechanically, which makes them consequences in the model which generates not merely ZF but others, as updated and extended. The hard part is still expressing that the - and this is very hard for me - orderings exist within a field or area of not-orderings which extend toward a limit of fixed, so not only countable but countable efficiently, which allows different limits as needed.

I have no idea if that was good. I havent thought about that area of explanation for a long time. Applying Not at the identity level. This is starting to connect to patterns, which is one of the grails.

My brother soothed me with physical demonstrations today. He can now clench his right side into ideal pose, which I have to say looks pretty good, with definition appearing more and the extensions having softened the tone of my muscles and the stretching working the skin to contract. That pose today is the one I’ve been looking for; it tightens the lower rib cage and stiffens the entire right side perspective into idealized man form. He was very happy. Then he showed me he figured out how to balance on the right foot by holding his left leg and fully extending and retracting it multiple times. That was a shock. The stuff he can do across himself is amazing.

That’s a layering I’ve largely set aside; the halves within and their identifications. My left hand is my brother’s hand, which is why I’ve long associated it with you. I just didnt have sufficient density of labels populated yet. My right became mine because I became so deeply involved in the transition across handedness. I had no choice but to become involved because the visible triangular was through me. And I associate the other triangular with you. That’s always been where it pointed, and then you became that pointer, which is hands, which are my favorite of your extremities. I’m typing while toasting bread: the 13 disappears into the selection of direction. I just saw it: the scale closeup enlarges and slows so you can see you racing around the house, with you not just getting smaller as the scale away enlarges but maintaining a sufficient pulse to identify where you are when it’s slow enough to see where you are, as that appearance of you shrinks so the pulse disappears into the directional cue with the slightest adjustment or sensitivity.

I connect this to CM64. Never thought I’d type the naive level model statements again. That invokes a process by which you run around the outside, which requires a more stationary existence for the house. It can be rotating, which mean this can be invoked by rotating the house and you running against it like a treadmill, so you adjust where you are by whether you go faster or slower than or the same as the counter-rotation. That is literally just varying counting speeds, which occurs because those speeds occur within an informational limit. That limit then becomes your capability to run as 13 against the treadmill. That sets a strategy of intentional slowing to allow the treadmill to rotate to the place you want the long way around. That seems to be crucial: it rotates the ++ quadrant through the others within each step, where step would be you start to run to stop the wheel so it halts you where you need to be, dropping in like an angel from above. This exactly matches the experimental manner of determining light speed: rotating mirrors until the stream is continuous over a long enough stretch that you deem it the limit, or equivalent extrapolations. Anything less invokes Not. That works within areas and thus within volumes, etc.

Amazing how fast my legs have been softening in tone as I’ve been extending. Extending the structures of my right leg has been torturous. Right leg, left side of brain, which puts you on the right. I’ve been extending my hands and feet as the restrictons have settled there, which shows progress in process not only result. The stuff my brother is doing ... whoa, I missed the cross-connection: who is my left side brain? That’s the same issue as above: I’m in there because I had to be in there, so much of this has been a process of getting me out of there so my brother unifies as I unify as we unify together.

Why CM64? Because I just realized that contains the lower case versions and mixtures that define the core transitive identity matrix. Here it renders as CM, cm, Cm, and cM. The first is an enlarging bigger than the second or the second is going the other way, and shrinking or enlarging relative to the other defines the C as the endpoints where choice occurs, big or little. This reduces M to m because the model interior function goes into the points. The second is small c, large M, which says choice within the model interior function. That enables the cross relationships, which draws the hypotenuse, which connects to the layers alternating like a cake in squares. I’ve never done that before with that degree of clarity. This allows application of different C’s: choice, context, counting, color, capability. It’s more obvious to pick a letter like C than to use a symbol to indicate that it’s ordinal and cardinal, meaning it counts across choice, context, etc. and within choice, context, etc.