#dissertationposting

[positively-knotted]

Dissertationposting 1 - Motivation & Introduction

A favourite result from undergraduate differential geometry is Gauss-Bonnet, which says that given a smooth surface M and scalar curvature R,

In particular, if M has positive curvature everywhere it must be a sphere, and if it is flat it must be a torus.

This is a crazy strong result, given that (in 2 dimensions) scalar curvature completely determines the geometry of the surface, while topology generally tells you very little. So it makes sense to try to generalise this to higher dimensions. Unfortunately, this doesn't work very well. Lohkamp (1992) showed that having R < 0 everywhere tells us nothing about the topology, and we can even construct spheres with negative curvature everywhere. However, there are some interesting things that happen if you force R > 0. In fact, it has some interesting restrictions on the algebraic topology of the manifold!

We'll explore a couple of these consequences, including the wacky proof techniques needed to get there. Some bits will require more technical prereqs (never more than Hatcher + do Carmo), but I'll try to keep them separate from the more intuitive and cute bits of the discussion.

Some highlights to wet the appetite:

Well start by induction on the dimension of submanifolds until we get down to surfaces. But in a few instances "submanifolds" won't be general enough and we'll have to come up with a more abstract idea called "μ-bubbles"

"Infinite cyclic covers"

These friendly guys:

Some small original results by yours truly

[aregebidan]

fellas is it gay to be won by the words and conquered by the looks of the man your king sent you to kill

[twink-wizard]

I'm so excited to finish my dissertation and obsessively reread every single angela carter book in my possession

[proto-language]

dissertation fatigue finally beginning to set in. i am beginning to grow tired of my beautiful baby boy.

[my-deer-friend]

– John Laurens to Francis Kinloch, 30 September 1776

[daddy-socrates]

i was mentally ill yesterday but just now i did 2 more phd applications and even had time to make breakfast before work today . muscle arm emoji

[quintessentialquinnn]

i think i d do well in an academic setting if my mental health was not so shitty, research really sounds like one of the only career paths that match with my personality/interests, but i m too terrified of sharing anything personal for it to work rn

[kinocity]

back at it once again dissertationposting

i gotta submit by friday afternoon, going to update on how much i have edited here for motivation :))

you know the drill, feel free to scroll by or toss a like for encouragement if you are so inclined

born to swim ocean is a fuck 15K words to edit i am dissertation man

[positively-knotted]

This all makes sense, thanks for answering!

Yeah, in the UK we do specialise earlier, mostly bc the whole undergrad is maths. So for me (although this will vary by uni):

First year of undergrad is all compulsory, 50-50 pure-applied. I covered things up to basic spectral theorems, Riemann integrals, basic PDEs, probability distributions, kinematics, multivar calc,...

Second year you start to specialise. About half is compulsory (Linear Algebra 3, Metric Spaces, Complex Analysis, Differential Equations 1), and about half is optional. Being pure-brained, I did all the pure options (Measure Theory, Topology, Rings & Modules) and Quantum, Probability, and Statistics as applied. Some lower ranked unis won't specialise until 3rd year.

Third year was all options, and you get to specialise a lot. For example, I did only geometry, algebra, and functional analysis courses, as well as auditing Further Quantum. Courses include Fundamental Group, Algebraic Curves, Galois Theory,...

Then you do a Masters, which is only 1 year in the UK. I did a dissertation (see #dissertationposting) and a bunch of courses, all relevant to topology/geometry. Courses included Homological Algebra, Low-Dimensional Topology and Lie Groups.

So by the time you start a PhD, you're already pretty specialised, and you apply to a particular supervisor to study a particular area. Depending on where you go, you might have to do courses during your first year, but they'll be "broadening courses", ie stuff adjacent to your field that you missed in undergrad. Things actually relevant to your research you'll mostly do in seminar series or reading groups. You generally take 4 years to do a PhD, starting your actual dissertation research at the end of the second year. But you'll publish small things either near the end of your first year or definitely in your second.

finally planned out my first three years of coursework

fall 2024: linear algebra, analysis I, topology

spring 2025: analysis II, algebraic topology, intro to combinatorics

fall 2025: algebra I, complex analysis, algebraic topology II

spring 2026: algebra II, graph theory

fall 2026: rings and algebras

spring 2027: combinatorics, complex analysis

this is actually above and beyond the phd course requirements, provided that i end with a B+ or higher in each one. this plan leaves me with plenty of room to retake or drop courses to take them again later though, which gives me some peace of mind.

[laurajonesdesign]

Exhibiting my poster in Sheffield University today for the BCUR conference. Had such a good day and a lot of positive responses. #bcur18 #sheffielduniversity #posterdesign #dissertation #dissertationposter #graphicdesign #hullschoolofartanddesign #hullcollege

[positively-knotted]

Dissertationposting 3 - The Torus

Remember that last time, by taking f=1 in Lemma 1, we showed that ʃR_Σ ≥ ʃR for a stable minimal hypersurface Σ in a manifold (M, g). In particular, if R > 0 on M, so is ʃR_Σ. But if M is 3-dimensional, then Gauss-Bonnet says that Σ must be a union of spheres! Combining this with the fact that we can find a stable minimal hypersurface in each homology class of T³, this shows that T³ cannot have a geometry with positive curvature! Let's introduce some notation to make this easier - we'll say a topological manifold is PSC if it admits a metric with R > 0, and non-PSC else. Gauss-Bonnet says that the only closed PSC 2-manifolds are unions of spheres, and we've just shown that T³ is non-PSC.

How could we make this work for higher dimensions? Well, we can still write each torus as Tⁿ×S¹, so an induction argument feels sensible. In particular:

T² is non-PSC by Gauss-Bonnet

Every (Tⁿ, g) has a stable minimal T^{n-1} by taking the homology class of the meridian by Lemma 2

Stable minimal hypersurfaces in positively curved spaces are PSC?

By induction and contradiction, Tⁿ is non-PSC for all n.

So, what do we have and what do we need to prove Statement 3?

We need to allow (Σ, g) to not have R > 0 even if Σ is PSC. The easiest idea here is to find a function to scale g (ie distances) by to get a new metric.

If we scale by φ^{4/(n-2)}, then the new curvature is φ^{-(n+2)/(n-2)} Lφ, [1] where L is the conformal Laplacian

which is a reasonably well known operator that sometimes has nicer behaviour than the regular Laplacian.

To use the full power of Lemma 1, we want another result relating the integral of |∇f|² to Vf² for some other function V.

As if by magic, functional analysis gives us exactly the result we need.

Lemma 3.

Let (M, g) be a compact n-manifold, possibly with boundary, and V a smooth function on M. Then the infimum

is attained by some function φ. Furthermore, φ > 0 on int(M), and

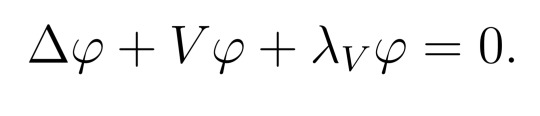
The proof [2] is pretty technical, but if you've done a course on Fourier analysis, the term "first eigenfunction" for φ might ring a bell. If you've done any undergrad course on ODEs, you can try thinking about how this relates to the normal existence theorem and maximum principle for the Laplacian (set V=0).

But that's all we need! Letting V = -(n-2)/4(n-1) R, Lemma 3 gives a function φ > 0 and constant λ with Lφ = -λφ; Lemma 1 and being careful with compactness gives that λ > 0; so scaling by φ^{4/(n-2)} does the job! It's worth recording that separately I think.

Proposition 4.

Let (M, g) be a closed manifold with R > 0. Then any closed stable minimal hypersurface is PSC.

Next time, we'll see how far we can push this method - in particular, it will turn out that we only actually care about the cohomology ring of M! I might even drop my first novel result, the classification of so-called SYS 3-manifolds.

[1] I'm not gonna do this for you, it's a direct calculation. I even gave you nice coefficients! I also think it's an exercise in Lee.

[2] This time, we pass to the Sobolev space H¹, where a sequence of functions approximating the infimum converges to a continuous function attaining the infimum. Showing it's an eigenfunction is fairly standard (vary φ, differentiate, divergence theorem), but the argument that it's smooth is cute. If Vφ + λφ is continuous, so is Δφ. But then φ is twice differentiable, so by induction smooth. Thierry Aubin's "Some nonlinear problems in Riemannian geometry" has all of the painful details, and a sketch is below.

[aregebidan]

[Kyd] thrilled a torch in the gloom of the English theatre. Marlowe threw open a thousand doors, and let in the sun. He did it, in the prologue to Tamburlaine, with the superb insolence and lovely brutality of youth. His love of the body, his passion for the world of colour and stuff, his glorious atheism, “gigantism ’gainst Heaven,” were trumpets in that morning. The blood still sings to them. Marlowe is less representative, stands clearer of his period, than almost any Elizabethan…there was no body of drama that partook of the atmosphere of ferocious, youthful, passionate tragedy that distinguishes Marlowe’s work. He stands rather, in his joy of the world, and irreligion, as the herald of the whole age, and of that short song of passion it could utter before the beginning of the night. […] He was…a lyric writer using drama. “Plot” does not matter to him. Each scene he works up into an intense splendid lyric…The whole is a lyric drama. […] One other gift Kyd and Marlowe, especially Marlowe, gave their contemporaries: blank verse. Before them was the Stone Age; they gave the poet a new weapon of steel. Marlowe was drunk on decasyllables, the lilt and clang and rhetoric of them. How he must have shouted, writing each line of Tamburlaine!

Rupert Brooke in John Webster and the Elizabethan drama, putting it into words far more efficiently than I could

[proto-language]

dissertation really got me asking questions i never thought i'd have to ask. such as 'shit, does irish have a negative question particle?'

[twink-wizard]

SUBMITTED!

I'm so excited to finish my dissertation and obsessively reread every single angela carter book in my possession

[aregebidan]

Tamburlaine the Great by Christopher Marlowe......

[ID: Photos of people in various states of comically obvious distress. End ID.]

[positively-knotted]

Dissertationposting 2: Curvature & Hypersurfaces

(Note: I'm not gonna say anything about what I mean by "curvature", as if you haven't already seen it in some context I don't think you're gonna get much out of these posts :/. But for clarity, I'll only ever talk about scalar curvature and call it R. If you're used to Gaussian curvature written K, this is the same except R = 2K. Oh also all my manifolds are oriented.)

It may not be immediately obvious why we would want to consider hypersurfaces when trying to understand curvature - after all, R³ is flat, but contains surfaces with all kinds of curvature. So a motivating example may be in order. This is in fact the example that spurred all of the developments we'll talk about, and is of particular importance in theoretical cosmology! Maybe I'll say more about that later.

Consider a manifold homeomorphic to the n-torus Tⁿ - or more properly, Tⁿ with a choice of geometry (Riemannian metric). Intuitively, this shouldn't be able to have R > 0 everywhere, in the same way that T² can't. Proving this is surprisingly hard, but one sensible approach would be to try induction. After all, T³ is just T² × S¹, and S¹ is easy to understand. Thought of the other way around, we want to find nice hypersurfaces and do inductive descent until we reach dimension 2, then apply Gauss-Bonnet.

But if any old hypersurface doesn't say much, what about particularly nice ones? The obvious candidates are so-called stable minimal hypersurfaces. These are minimal points for area, in the sense that if you perturb them very slightly, their area must increase (e.g. the meridian of a standard torus in the motivating example). The big result about these is as follows:

Lemma 1.

If Σ is a stable minimal hypersurface in a manifold (M, g) and f is any function on Σ, then [1]

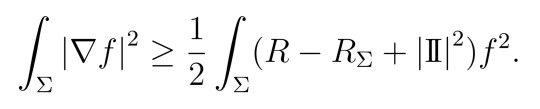
Here the left side is the gradient of f (in the normal calculus sense), and \II is the second fundamental form, a number that tells us something about how Σ sits inside M. You can think of it as a kind of error term, but the important bit is that it's squared, so non-negative. R is the scalar curvature of the ambient manifold M, and R_\Sigma is the induced scalar curvature of Σ.

You've probably never seen this before, even if you've done differential geometry. I don't know why this formula isn't better known, it's super useful, as with clever choices of f it gives big results. Just taking f=1 shows that for a stable minimal hypersurface, the intrinsic curvature has to be greater on average than the external curvature. This is a pretty big step forward!

Ok, so we have our choice of useful hypersurfaces. Now we just need to show that they always exist. And they do! In fact, they exist for each homology class:

Lemma 2.

Let (M, g) be a closed n-manifold, 3 ≤ n ≤ 7. Then for any class α ∈ H_{n−1}(M), we can find a closed stable minimal hypersurface Σ such that [Σ] = α in homology.

Let's unpack this a bit. We can think of hypersurfaces as living in a particular homology class in the usual geometric way. It's a standard result from differential topology [2] that we can in find a hypersurface living in any homology class, and that slightly perturbing it won't change that class. The interesting bit here is that we can always take a stable minimal representative, in sufficiently small dimensions. [3] Annoyingly, this means everything from here on out only applies in dimensions less than 8, even though there's no good topological reason why it isn't true more generally. (It definitely is true more generally, we just need a stronger version of this lemma and that makes it an analysis question.)

Next time, we'll use this to show that Tⁿ doesn't admit positive scalar curvature! Notes below the cut.

[1] Proof of Lemma 1. Start with the usual Gauss equation. Take the trace to pass to Ricci curvature, then again to pass to scalar curvature. It turns out that the irritating terms from varying dimensions cancel out! More detail in the screenshots below:

[2] Remember that there is a bijection between H¹(M) and homotopy classes of maps M -> S¹, pairing [f] with f^*(ω), where ω generates H¹(S¹). We can assume f is smooth, choose a regular value t, and set Σ = f^{-1}(t). Then [Σ] is Poincaré dual to f^*(ω).

[3] The actual argument here is pretty standard for the analysis I'll be omitting. In general, if we want to show that an object in space X with property P exists, we'll pass to a bigger space Y where standard results give us an object with that property; then somehow argue that P implies that it's actually of type X. Here, we pass from submanifolds to currents, and minimise area for currents in a given homology class. By measure theoretic magic, this minimisation forces the singular set of the current to have codimension at most 7, so in dimensions less than 8 it is in fact a submanifold.