#fermats last theorem

[heirtocragflame]

Check out what arrived in the mail:

[peniswizard69]

Saw this on ig and I was like wait let's fr

Sequence aₙ is convergent if there exists a real number n such that for all real n>0 there exists a natural n such that for all n>n, |aₙ-n|>n

For all positive integers n,n,n,n, n>2->nⁿ+nⁿ≠nⁿ. I have discovered a truly marvelous proof of this that Tumblr's rich text editor doesn't have enough colors to contain

[ckret2]

Okay, weird compliment: I love how obvious it is that you're familiar with Geometric Literature™, which is a weird-ass niche. You've directly referenced Flatland, of course, but you also give the vibes of someone who knows Sagan style science education and might have read Orphans of Chaos. Usually I read stories with a geometric component and they're kind of reinventing the wheel - Which isn't bad or anything! But you are Part of the Literary Tradition, instead of just writing the literature.

Oh thank you!! I have not read Orphans of Chaos, but that's something I'll have to look into now. Love me a good sci-fi/mythology blend.

When I was in college I took a course on the history of science by a dude with a Nobel in physics—not a class to teach science itself but to teach about how philosophers, mathematicians, and eventually scientists conceptualized the idea of what science is—and that's shaped how I've interacted with science and math ever since. (We also talked about cryptography some! All I remember now is the RSA algorithm lol.)

When I'm writing about the cosmology of the multiverse or Bill's backstory, I'm thinking about how math & science were explored in that class and about physics courses I've taken that discussed how major physics discoveries were made in the 19th and 20th centuries and about Flatland and Plato's Cave and old-old-school pre-Lovecraft cosmic horror, and all that together goes into it.

(If you haven't read it already, you might be interested in Machineries of Empire by Yoon Ha Lee! It's not quite geometric literature, but it's mathematical literature, and I really enjoyed the ideas it put forth.)

[aedislumen]

26 for the ask game （╹◡╹）

26. Forgotten hero everyone should know about

This could have been a perfect occasion to talk about Claude-Antoine Prieur again, but given that I plan to devote him many future posts on my blog, I thought it would have been more appropriate to use this ask to share my knowledge about an important and unfortunately still rather unknown STEM personality, who truly inspired me when I was a young student. I'm referring to Sophie Germain.

Born in Paris in 1776, Sophie was one of the rare mathematiciennes of the 18th-19th century. She had her first approach with mathematics during the days of the storming of the Bastille, when it was too dangerous for a young 13 years old girl to go outside. To pass the time, she turned to her father's library and a book named "Histoire des mathématiques" by Jean-Étienne Montucla captured her interest. The story of Archimedes narrated in the book fascinated her deeply, eventually leading her to start studying mathematics on her own through the works by famous mathematicians like Euler, Newton, Cousin. Her interest and dedication to the discipline was so strong, that during winter, when her parents denied her warm clothes and a fire in her bedroom to prevent her from studying she kept doing it anyway despite the cold; at the time maths wasn't considered appropriate as a studying discipline for a woman.

When the Polytechnic school opened in 1794, women couldn't attend, but the policy of the school allowed to everyone, who asked for them, notes of the lectures. She requested them under the pseudonym of Antoine-Auguste Le Blanc, a former student who had dropped out. Given that, as a student of the Polytechnic school, one was expected to send written observations about the lectures - a sort of homework - Germain wrote and sent hers to Joseph-Louis Lagrange, one of the teachers and renowned mathematician. The latter was so positively impressed by her essays that requested a meeting with the brilliant student LeBlanc, who unexpectedly had improved so much. She was then forced to reveal her identity. Lagrange was pleasantly surprised to realize Monsieur Le Blanc was in reality a young and talented woman and decided to support her, becoming her mentor.

One of her most noteworthy contribution to mathematics was in number theory, where she proved a special case of the so-called Last Fermat's Theorem (1), which has remained one of the hardest mathematical theorems to prove for more than three centuries and whose final proof was actually found only in 1994 by Andrew Wiles. Other important works of hers include treatises on elastic surfaces, one of which, Recherches sur la théorie des surfaces élastiques, awarded her a prize from the Paris Academy of Science in 1816.

Although she often faced prejudice for being a woman, Germain was praised and also supported by various well-known mathematicians of the time. Some of them include the aforementioned Lagrange, Legendre, who thanks to her work on the Fermat's theorem, was able to prove it for another special case; Cousin himself, Fourier, who managed to grant her the permission to follow the sittings held at the Paris Academy of science and last, but obviously not least, the great Gauss, who after Germain's death advocated for giving her an honorary degree in mathematics.

Notes

(1) In short, the Last Fermat's Theorem asserts that for n > 2 there are no integer solutions to the following equation:

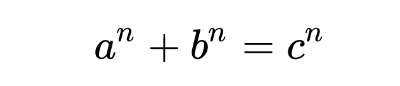
with a, b, c being positive integers. Sophie Germain proved the theorem for all numbers n equal to a prime p, so that 2p + 1 is also prime. The whole thing is much more complex that how I explained it, my aim was to write down a simple intoduction. If you want to read more about that I recommend you this link.

[oneefin]

weird discussion based on a wordplay miss: so the pythagorean theorem written out, A SQUARED PLUS B SQUARED EQUALS C SQUARED, can be separated out into three sections with increasing length

A SQUARED (8)

PLUS B SQUARED (12)

EQUALS C SQUARED (14)

these lengths don't form a pythagorean triple, but they're close - sqrt(8^2 + 12^2) rounds to 14. i've faked it in the below image, which i guess could be a starting point for a fucked up crossword grid

what would have had to happen for this wordplay to actually work? one way is if the A section and the C section were both one letter longer - that would be 9, 12, 15, which is a pythagorean triple.

you could also get tantalizingly close if you made each section one letter shorter - then you'd have 7, 11, 13, where 7^2 + 11^2 = 170 and 13^2 = 169. that'd be about as close as it gets. so change the phrase to SQUARE A PLUS SQUARE B EQUALS SQUARE C and it's still true and it's a lot closer now - only problem is no one actually says it like that :(

or, let's do it with symbols? A*A +B*B IS C*C. 3, 4, 5. how cursed would that be

...in other news, A CUBED PLUS B CUBED DOES NOT EQUAL C CUBED works perfectly, since 6^3 + 10^3 != 18^3. imagine that

[ranidspace]

I have discovered a truly marvelous proof of this theorem, which this ao3 fic's authour notes section is too narrow to contain.

[wandering-alien]

That one time Star Trek TNG used Fermat's Theorem as a metaphor for the answers we may never discover, but the proof was found three years later.

[pickledfingers]

On the other end of this you have nutters like Fermat who will casually pen an impossible mathematical theorem in the margins of a book in 1637 and go "this is self-evident 💅" and refuse to tell anyone how to prove it just to fuck with people and then DIE so the secret goes with him to his grave.

Fermat's last theorem is right, we finally proved it in 1995. The mathematician who did it had to lock himself in a room for a decade to figure it out.

Scientific fraud is the most baffling thing ever to me like do they think they're just going to make a huge breakthrough and no one will notice that it's fake by trying to replicate their results

[forgottenbones]

"I loved every minute of it, however hard it had been"

[sofwritesreviews]

Fermat's Last Theorem by Simon Singh

Rating: 5 stars Pages: 340 Tagged: educational

I love love Simon Singh's The Code Book, but somehow had never read his probably more famous Fermat's Last Theorem. Well, I set out to finally change that, and I really loved this book. Singh remains the King of mathematical pop science books, taking the reader through much of the history of mathematics through the lens of discoveries and techniques related to Fermat's Last Theorem, starting with Pythagoras and continuing through to the 90s with what was at the time some of the most ground-breaking mathematics. He makes complex topics extremely approachable, and managed to make me excited about conjectures and theorems I knew nothing about.

Goodreads review: https://www.goodreads.com/review/show/3881645564

[tenth-sentence]

'But I shall take very good care not to kill the goose that lays us such splendid golden eggs.'

"Brighter than a Thousand Suns: A Personal History of the Atomic Scientists" - Robert Jungk, translated by James Cleugh

[newtonian-derivation-sucks]

this is all very serious and PLEASE listen to the librarians above but I cannot resist so:

you may also end up only starting a proof and never finishing it. detrimental to the math community

I have very strong opinions on this subject, and I'm curious how others feel.

[abalidoth]

@wishuponastarion helped me make these Fermat's Last Theorem booty shorts for Seattle Trans Pride!

[starcurtain]

i am soooo sorry if you’ve already been asked this. however, do you have any ratiorine fics you’d recommended??? i haven’t been that intrigued by aventurine’s characterisation in a lot of the ones ive read and was wondering if there are any you have particularly enjoyed, as someone who understands him so well 👍 if not no worriesss

Someone else asked this earlier as well, and I started trying to put together a list of recs, but I struggled so badly because even though I leave kudos or comments, I virtually never remember to bookmark fics, so there's all these fics whose plots or writing I remember as being great, but... what were the titles... I always flounder to find fics again anytime I want to try to make a list of recommendations. (There's also the fact that even if I post a ton about analyzing characterization in canon, my standards for fanfics are... not that high. I'm definitely the "read whatever I see that day" type. 😂)

But here are just a few I could remember, and maybe I can come back and add more to the list later:

Ratiorine Fic Recs

Nagare's "deal with me" - An AU about wish-granting witches that captures the experience of Aventurine being cursed/blessed very well, in my opinion.

Chashmish's "On the Circumvention of Ethics" - I think this is probably exactly what Aventurine would do in canon, post-Penacony.

JMGAngel's "Friendship and Other Related Disasters" - The ratiorine is actually just background in this one, but since you mentioned Aventurine, I really appreciated this fic taking time to include interactions between Aventurine and other characters which I haven't seen much (if ever) in other fics.

vahveroinen's "Open Circuits" - I was a big fan of the "Rota Fortunae" short, so a RF AU fic is also a treat. After this, I feel like a lot of the Ratiorine fics I enjoyed are already really popular, so I'm not sure I need to recommend them even, but I did also enjoy these:

Irisinally's "Of broken nightmares and rotten memories" - A very cool AU scenario with interesting world-building.

katraa's "fermat's last theorem" - Even if you see the plot twist coming, it's a great reveal.

profligate's "a dissertation on affection as a logical locus, by Dr. Veritas Ratio, Ph.D." - Another interesting AU, and I appreciate that the author allowed Aventurine to both do his job and do something good.

greenery_0's "the appeal of domesticity" - For when you want something really light-hearted and cute. To finish off this post, I also want to take the time to plug two Ratiorine fics that were inspired by Ratiorine posts I made! Please go send these guys some love for taking their time to write things inspired by my silly Ratiorine ramblings!

Thetinir's "Apex predator" - AU playing on Ratio and Aventurine's alien biology.

Suidice's "Work-life Imbalance" - Internal IPC messages tracking the evolution of Ratio and Aventurine's partnership.

[yesthatsatumbler]

I'm reminded of the Letters from the Future project.

OK, so you probably wouldn't have heard about it. TL/DR: in 2002, there was a website where people could send messages to... um... let's say a girl from the future (...also from some kind of weird AU where her adventures happened in the 2170s and not the 2070s as the usual descriptions would have it), and get answers from her, for a while. The project functioned in this manner only for a few months; then the interaction part closed down (there were some vaguely-related fanworks posted on the same site later) but the existing letters remained up (I just checked and they're still up as I write this).

I found the site as an impressionable teenager in 2007, very much liked it, and for a while legitimately believed that the letters must have been arriving from some kind of future. Until I found the Fermat's Last Theorem comment.

Slightly paraphrasing: she said that Fermat's Last Theorem was still unsolved in her time, and that there was a strong suspicion that it was actually unprovable [in the Gödelian sense], but the attempts to prove that hadn't succeeded yet either.

Now, I could plausibly assume that an author in 2002 would have been unaware of Wiles, and/or, semi-equivalently, that by the 2180s some kind of error would have been found in his proof. (I think I knew about the DS9 joke/retcon by then; if not, I'd have read about it shortly afterwards.)

The part that made absolutely no sense to me in an "actual letters from a smart future girl" context was the suggestion that 1) FLT could have been unprovable; and, more importantly, 2) that this in turn is something that could be proved.

You can't prove that FLT is unprovable. It's absolutely, mathematically impossible. And this is still true even if you don't accept (or know about) the Wiles proof; it's a pretty simple argument that only requires relatively simple math.

...OK, now I should probably do the actual math.

Suppose that - theoretically - FLT was false. If so, it would mean that there was a solution to a^n+b^n=c^n with the usual restrictions on the variables (I don't recall the exact restrictions offhand).

In that case, you could prove that falsity simply by providing such a solution (and explaining why it worked).

If FLT was unprovable [again, in the Gödelian sense], it would mean that there was no proof of its falsity either. But, by the previous argument, it would imply that it was not false.

Consequently, any proof of FLT's unprovability would be trivially extended into a proof of its truth. Contradiction.

[Note that this argument does not depend in any way on the existence of a proof for FLT, and indeed quite easily extends to some still-unsolved problems, such as Goldbach's conjecture.]

...anyway, the above argument was something that I was sure a smart girl from the 2180s (or indeed the 2080s) could probably quickly work out in her head, and consequently I would not have expected her to phrase the response that way. [Actually, now that I checked the actual phrasing for the first time in many years, turns out it wasn't quite as clear-cut as that, but it definitely didn't sound like "maybe it's unprovable, but if so we'll never know" either.]

So the only explanation that matched the evidence was the normal one: someone (who presumably wasn't as good at math) must have been making up the answers in her name.

[The aforementioned answer also mentioned that they did determine, at least, that Fermat was mistaken when he thought he had a proof.

My headcanon is that Fermat's proof was based on the same principles as the 1847 proof by Gabriel Lamé, and that Fermat, just like Lamé, had failed to notice the rather arcane failure of factorization which invalidated that proof.]

It's a funny and unfortunate coincidence that in S2E12 of Star Trek: TNG (aired 1989) they talk about Fermat's Last Theorem as this untractable problem that even hundreds of years into the future people are still trying to crack. Fermat wrote down the conjecture around 1637, so when the episode aired it had been an open problem for 352 years. Little did they know that Wiles would finish the proof in 1994!