#nonstandard arithmetic

[ahuactl]

on mathematical models

the question “is math invented or discovered?” remains to be the most contentious questions in mathematics.

a significant portion of people including mathematicians believe that mathematics holds objective truth insofar as their models, theorems and equations tell the truth about reality in which the Subject: their proposition exists independently of them. this position is familiar among those in the Platonist or Realist traditions of mathematics. common knowledge states that any proposition such as  P: 1 + 1  = 2  is true in which ever universe it is stated in such that its truth is not constructed upon the confines of our society and more strongly, not in our minds or cognitions.

i will present my argument here on why i disagree with this view. first, propositions like P: 1 + 1  = 2 are certainly not true in every construction of a mathematical system. for example, in boolean algebra and nonstandard number systems. even non-Platonist mathematicians would quickly disagree with this as they would claim that the Platonist view holds that the truth of a proposition exists not solely but with the pair (P, S) whereas P is the proposition and S is the system in which it is considered to be in. on such note, this leads me to my next argument.

from the development of set theory in the 19th century, it was discovered by mathematicians that mathematics as a field was built on shaky logical foundations (re: Russel’s Paradox). this thus necessitated the construction of a new structure which must possess the power to rebuild mathematics. this new foundation came with the introduction of ZFC. it is an attempt to systematically rebuild the previously known and accepted results of mathematics while working to eliminate the logical inconsistencies of previous naive set theory. from how it was made, ZFC does not posit the truth of any propositions insofar that it exists as starting axioms in which rules of inference can be applied. as with any theories of logic, its axioms must be decided and chosen. it could be noted that these axioms were posteriori in a sense that they were built to solve the issues such as Russel’s Paradox. it can then be argued that the process by in which these axioms were chosen is contingent upon the values of the persons that chose it as well as the developed culture of mathematics. in fact, it is by no means that ZFC is only the possible theory of mathematics (e.g. Model Theory, Category Theory). no matter the “objective” metaphysical existence of mathematical objects, by the way mathematics was built and practiced, these starting axioms still remain a choice.

to reiterate, the way mathematics has been agreed to be used by mathematicians, whichever system set in place still remains a choice. this reveals its use as pragmatic: the system, that is, ZFC was adapted because it works. this naturally extends out from its foundations to concrete mathematical objects studied in abstract algebra, analysis, etc. for example, a group is not just a set with specific rules with its binary operation; the construction of the properties that denote a Group came a posteriori in a way that it was discovered that the set of properties in the first place proved to be a useful abstraction to study. 

on a related note, i would argue that the existence of abstract mathematical objects actualize themselves by our need and desire for the world to conform to standard rules as appeal to our intuition and senses. the truth value of P: 1 + 1  = 2 in (P, S) in an arithmetic system S signifies an essence in which it “makes sense” that combining abstract objects  result to a set in which it succeeds singular objects by the value of each one of those objects. the value of (P, S) does not reveal a Platonic truth of our universe but instead a declaration of common sensical deductions. in such, a mathematical statement is a “model” the same way a bachelor is “unmarried”.

on usage:

regardless of the metaphysical existence of mathematical objects, it, as a system, is undoubtedly one of the finest works of humankind. i advise that one ought not to use this powerful tool to make claims of absolute truth. in a sense, the existence of mathematical objects remain irrelevant to how it ought be used. one should not at all invoke mathematics to justify repressive systems and to cause grave harm to humanity. as a tool, it must not be used for evil. one must always remain cautious of individuals who use mathematics as arguments by certainty. these individuals who swear by the sharp sword of mathematics is most likely using it to silence thought and keep one from questioning. always look at the mathematics; an equation is not just a set of symbols that denote some property; it is a theory of the world and this theory must be met with most criticisms when it is being used to make claims for human policies. look at the mathematics, specifically which assumptions were made by the ones who present them: it must reveal the true character of such persons.

[max1461]

@transgenderer I've done some amount of model theory (not a huge amount, I took a model theory class in undergrad and then I've sort of intermittently read about nonstandard models of arithmetic and whatnot since then). I feel like… there's definitely some sort of "thing" "going on" with the model theory implications. I just feel like all the discussions I see of nonstandard models of arithmetic are kind of confused, or like, they leave me feeling that there's something crucial they are failing to say. Uh, hard feeling to put into words but I'm sort of dubious of drawing any philosophical conclusions until I "get it better", and it might be the case that nobody anywhere has quite addressed the right set of things to quell my uneasiness.

Like, I made that post a while ago about how you can maybe think of second order PA as a function (is it a functor? maybe...) from "notions of property" to "notions of arithmetic". Like one way to formalize "properties" is as ZFC sets, and then from there SOPA gives you a particular canonical model of PA (the unique second-order model). But it's only canonical from within ZFC, because "from the outside" you can have "nonstandard" models of ZFC that give different canonical models of PA...

I don't know what "standard" and "nonstandard" mean, I guess that's the crux of it. No one can give me a philosophically or mathematically adequate explanation of what they mean. But they have to mean something because we're talking about them, right. Maybe not. Ok, no—they are linguistic expressions used fruitfully by mathematicians, so they have to like, do something coherent in mathematical discourse. But I don't know what it is. I think I have to figure out what it is by fucking around with logic a bunch, like internalizing systems inside other systems and mulling very hard over what is going on, you know, until I figure out what these expressions are doing. Because no one has provided me with an adequate explanation. And then, uh, maybe after that I'll know what even the weirdness is with Gödel and model theory. Because there's weirdness for sure but I can't put my finger on it. I think it's like you said in your post, someone needs to come in with like a sufficiently careful philosophical eye but also a sufficiently careful mathematical eye to be like, ok. Is there a problem here? Is there a problem officer? Like am I being detained, and if so, what for?

If someone has actually done that I would love to be made aware.

[tilde-he]

Epistemic status: full of question marks. exploratory? dreaming big, perhaps of things impossibly big. Right, so,

I saw a couple papers (which I didn’t entirely understand, but seemed neat) about different theories of probabilities which use infinitesimals in the probability values (one of which was this one (<-- not sure that link will actually work. Let me know if it doesn’t?), and the other one I can’t find right now but was similar, used the same system I think, though it also dealt with uniform probability distributions over the rational interval from 0 to 1) and they built their stuff using nonstandard models of the natural numbers, where, if I’m understanding correctly, they got some nonstandard integer to represent “how many standard natural numbers there are”, or something like that. Also, they defined limits in a way that was like, as some variable ranging over the finite subsets of some infinite set gets larger in the sense of subsets, then the value “approaches” the limit in some sense, and I think this was in a way connected to ultrafilters and the nonstandard models of arithmetic they were using. I did not actually follow quite how they were defining these limits.

(haha I still don’t actually understand ultrafilters in such a way that I remember quite what they are without looking it up.)

Intro to the Idea:

So, I was wondering if maybe it might work out in an interesting way to apply this theory of probability to markov chains when, say, all of the states are in one (aperiodic) class, and are recurrent, but none of them are positive recurrent (or, alternatively, some of them could be positive recurrent, but almost all of them would not be), in order to get a stationary distribution with appropriate infinitesimals?

Feasibility of the Idea:

It seems to me like that should be possible to work out, because I think the system the authors of those papers define is well-defined and such, and can probably handle this situation fine? Yeah, uh, it does handle infinite sequences of coin tosses, and assigns positive (infinitesimal) probability to the event “all of them land heads” (and also a different infinitesimal probability which is twice as large to the event “all of them after the first one land heads (and the first one either lands heads or tails)” ), and I think that suggests that it can probably handle events like, uh, “in a random walk on Z where left and right have probability 1/2 each, the proportion(?) of the steps which are in the same state as the initial state, is [????what-sort-of-thing-goes-here????]”, because they could just take all the possible cases where the proportion(?) is  [????what-sort-of-thing-goes-here????], and each of these cases would correspond to a particular infinite sequence of coin tosses, which each have the same infinitesimal probability, and then those could just be “added up” using the limit thing they defined, and that should end up with the probability of the proportion(?) being [????what-sort-of-thing-goes-here????].

Building Up the Idea:

So, if that all ends up working out with normal markov chains, then the next step I see would be to attempt to apply it to markov chains where the matrix of transition probabilities itself has values which are infinitesimal, or have infinitesimal components, and, again, trying to get stationary distributions out of those (which would again have infinitesimal values for some of the states). Specifically, one case that I think would be good to look at would be the case where a number is picked uniformly at random from the natural numbers and combined with the current state in order to get the next state (or, perhaps, a pair of natural numbers). Or from some other countably infinite set. So, then (if that all worked out), you could talk about stuff like a stationary distribution of a uniform random walk on Z^N and stuff like that.

The Idea:

If all that stuff works out, then, take this markov chain: State space: S∞ , the symmetric group on N, or alternatively the normal subgroup of S∞  comprised of its elements which fix all but at most finitely many of the elements of N. Initial state (if relevant) : The identity permutation. State transitions: Pick two natural numbers uniformly at random from N, and apply the transposition of those two natural numbers to the current state. Desired outcome: A uniform probability distribution on S∞ (or on the normal subgroup of it of finite permutations)!!!  (likely with infinitesimal components in the probabilities, but one can take the standard part of these probabilities, and at least under conditioning maybe these would even be positive.)

Issues and Limitations:

Even if this all works out, I’m not sure it would really give me quite what I want. Notably, in the systems described in the papers I read-but-did-not-fully-understand, for some events, the standard parts of the probabilities of some events depended on the ultrafilter chosen.

Also, if every (or even “most”) of the permutations had an infinitesimal probability (i.e. a nonzero probability with standard part 0) in the stationary distribution, that probably wouldn’t really do what I want it to do. Or, really, no, that’s not quite the problem. If the exact permutations had infinitesimal probability, that could be fine, but I would hope that the events of the form “the selected permutation begins with the finite prefix σ” would all have probabilities with positive standard part.

But, it seems plausible, even likely, that if this all worked, that for any natural number n, that the probability that a permutation selected from such a stationary distribution would send 1 to a number less than n, would be infinitesimal. (not a particular infinitesimal. The specific infinitesimal would depend on n, and would increase as n increased, but would remain infinitesimal for any finite n).

This is undesirable! I wouldn’t be able to sample prefixes to this in the same way that I can sample prefixes to infinite sequences of coin tosses.

(Alternatively, it might turn out that the standard part of the probability that the selected permutation matches the identity permutation for the first m integers is 1, as a result the probability that a transposition include one of the first m integers being infinitesimal, which might be less unfortunate, but still seems bad? I’m less certain that this outcome would be undesirable.)

I think that, what I really want, would require having a probability distribution on N which, while not uniform, would be the “most natural” probability distribution on N, in the same way that the uniform distribution on {1,2,3,4} appears to be the “most natural” probability distribution on {1,2,3,4}, when one has no additional information, and also that said distribution on N would have positive (standard parts of) probabilities for each natural number.

To have this would require both finding such a distribution, and also showing that that distribution really is the “most natural” probability distribution on N. Demonstrating that such a distribution really is the “most natural” seems likely to be rather difficult, especially given that I am uncertain of exactly what I mean when I say “most natural”.

...

If I should have put a read-more in here, sorry. I can edit the post to put one in if you tell me to. edit: forgot to put in the “σ” . did that now.

[disconnecteddots]

2 + 2 = ? : using nonstandard arithmetic is easy to abuse

If you're not familiar with the 2+2 Twitter War of 2020, here is a thread about it from the anti-woke side.

Progressives pointed out various scenarios or mathematical contexts where 2 + 2 might not equal 4. Depending on how you saw it, these were either interesting ideas to consider or obnoxious pedantry to ridicule.

I want to write briefly regarding this particular tweet by one Professor Kareem Carr:

I don’t know who needs to hear this but if someone says “2 + 2 = 5”, the correct response is “What are your definitions and axioms?” not a rant about the decline of Western civilization.

Here's a brief introduction to "modular arithmetic" if you're not familiar. It works like a clock. On a clock, 9 + 4 = 1. 7 + 7 = 2. Since the "wrap-around" number is 12, this is called "modulo 12". But other moduli are possible. For instance, 2 + 2 = 1 modulo 3. The "wrap-around" number is 3, and 4 is 1 greater than 3, so the final answer is 1. The difference with a clock is that a clock goes from 1 to 12, but modular arithmetic starts at 0 and ends right below the "wrap-around" number. So 6 + 6 = 0 modulo 12.

In modulo arithmetic, numbers are always less than the "wrap-around" number, just like there's no 13 on a clock.

Now consider the following statements. I do NOT believe these statements. I am presenting them for rhetorical purposes ONLY.

0 people were killed in the Sandy Hook Elementary School shooting in December 2012.

Police only knelt on George Floyd's neck for 46 seconds on May 25, 2020.

I would simply say these are false statements.

But would Professor Carr respond, "what are your definitions and axioms?"

The first one is true... modulo 26. (26 people were killed in the shooting.) The second one is true... modulo 60. (Police knelt on Floyd's neck for 7 minutes, 46 seconds.)

And of course you could say "fewer than 100,000 Jews were killed in the Holocaust" without stating that you were using modulo 100,000 arithmetic, which by definition has no numbers above 100,000. "What are your definitions and axioms?"

Of course, the idea that no one was killed in the Sandy Hook shooting is in fact a notorious conspiracy theory. And I don't need to say anything more about Holocaust denial.

[cladeymoore]

Capture the Coin — Cryptography Category Solutions

Capture the Coin — Cryptography Category Solutions

By Jake Craige, Max Mikhaylov, Jesse Posner

In the last post of the Capture the Coin competition series we will dive into the solutions for our cryptography challenges. Also, feel free to revisit our other write ups in the series for Trivia, Blockchain as well as the Competition and Prizes announcements.

AES Encryption Flaw

By Jake Craige

This challenge presents you with the output of an encryption and asks for the message that was encrypted (plaintext) as the solution. It was encrypted with Ruby as follows:

def encrypt(message)

require ‘openssl’

# Encrypt the message using random key+iv with AES-128-OFB

cipher = OpenSSL::Cipher.new(‘AES-128-OFB’).encrypt

random_key = cipher.random_key

cipher.key = random_key

random_iv = cipher.random_iv

cipher.iv = random_iv

ciphertext = cipher.update(message) + cipher.final

# Encrypt the IV with AES-128-ECB

simple_cipher = OpenSSL::Cipher.new(‘AES-128-ECB’).encrypt

simple_cipher.key = random_key

encrypted_iv = simple_cipher.update(random_iv) + simple_cipher.final

{

ciphertext: ciphertext.unpack(‘H*’).first,

encrypted_iv: encrypted_iv.unpack(‘H*’).first

}

end

If you have worked with AES before there are a few parts of this that may stand out to you.

First, it uses the Output Feedback (OFB) mode of operation as seen by usage of “AES-128-OFB” in the prompt. There isn’t anything wrong with this on its own, but the Cipher Block Chaining (CBC) and Counter (CTR) modes are more common and in practice, authenticated encryption (AE) like Galois/Counter Mode (GCM) should be used.

Next, we see that the IV is encrypted and uses the Electronic Codebook (ECB) mode. IVs are non-secret values and do not need to be encrypted. The security of the block cipher relies on them being random, but not secret. Furthermore, using ECB mode for encryption is never what you want. It is meant to serve as a building block for other modes, but should not be used as a mode on its own.

Block Ciphers & Modes

Let’s review what block ciphers and modes are, as they are key to solving this problem. A block cipher is a deterministic algorithm that accepts a fixed size secret key and plaintext as input and outputs a fixed size output, called a block. They are used for encryption which implies they also have a decryption operation that accepts the key and ciphertext and returns the plaintext.

A block cipher on its own is not secure for encrypting more than one message because encrypting the same message twice would result in the same ciphertext, put another way, a block cipher is deterministic.

Why is this a problem? Let’s say an army sends the message “Attack at dawn” one day and their adversary figures it out. On another day, if the army sends the same message and the adversary is watching, the will know that an attack is imminent and can set up defenses.

Formally, we say that a block cipher is not IND-CPA secure (indistinguishable under a chosen plaintext attack). This means that if we have a service encrypting data and we provide it two separate plaintexts to encrypt, we should not be able to identify which one was encrypted from the ciphertext.

We solve this issue by introducing different block cipher “modes of operation”. The default is ECB which is insecure, and other modes make it secure by introducing randomness and chaining blocks together in various ways.

We’ll review the ECB and OFB modes as they are the what the challenge uses.

Electronic Codebook (ECB)

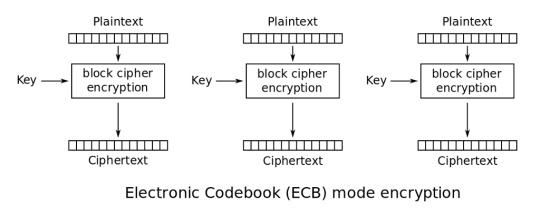
source: https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation#Electronic_Codebook_(ECB)

ECB mode works by splitting the plaintext into blocks and independently encrypts each block. The final ciphertext is the concatenation of each block ciphertext.

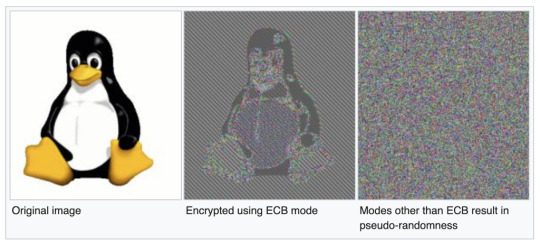
A popular example of why this mode fails at providing enough security can been seen with the “ECB Penguin” image. We see that even when the image is encrypted, you can still see the penguin. This is clearly an undesirable property of an encryption scheme. An ideal encryption scheme would make the encrypted image look random as seen in the third image. Modes other than ECB provide this.

source: https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation#Electronic_Codebook_(ECB)

Output Feedback (OFB)

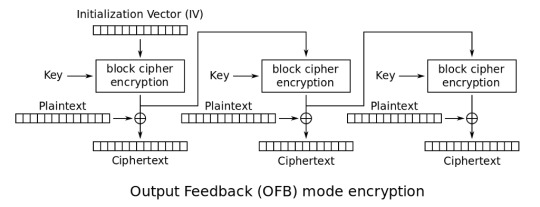
source: https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation#Output_Feedback_(OFB)

OFB introduces an initialization vector, exclusive ORs (XOR), and the ciphertext from the previous block is used as input to another. The IV is a random value chosen at the time of encryption and prefixed to the ciphertext. The combination of the random IV and chaining blocks together solves the issues we described with ECB.

The Solution

With an understanding of the block ciphers used in the prompt, we can review how they were used and find the solution. Recall that the two ciphertexts are generated are as follows:

The message is encrypted with a random key and IV using AES-128-OFB.

The same IV is then encrypted with AES-128-ECB using the same key.

Looking at the size of the message ciphertext, we can see that it is 16 bytes long which means the plaintext is exactly one block since AES-128 uses 128-bit blocks. Given this, we can describe the message ciphertext as Encrypt(Key, IV) XOR Message. For the IV encryption, ECB mode was used, so the encrypted IV is simply Encrypt(Key, IV). Due to the property of XOR where a XOR b XOR a = b, we can solve for the plaintext by Ciphertext XOR EncryptedIV which is equivalent to Encrypt(Key, IV) XOR Message XOR Encrypt(Key, IV) = Message.

The solution in Ruby can be found as follows:

message_ct = [“1b08dbade73ae869436549ba781aa077”].pack(“H*”)

iv_ct = [“6f60eadec7539b4930002a8a49289343a7c0024b01568d35d223ae7a9eca2b5c”].pack(“H*”)

message_ct.bytes.zip(iv_ct.bytes).map { |l, r| l ^ r }.pack(“C*”)

This correctly outputs the CTF flag “th1s is sec01234”.

ECDSA Nonce Reuse

By Jake Craige

This challenge is described as follows:

The data below provides two hex encoded ECDSA-SHA256 signatures using the secp256k1 curve for the provided public key. These signatures were generated using the same nonce value which allows recovery of the private key.

Your task is to find the private key and submit it (hex encoded with 0x prefix) as the solution to this challenge.

Pubkey (SER-compressed): 0x2341745fe027e0d9fd4e31d2078250b9c758e153ed7c79d84a833cf74aae9c0bb

Sig #1 (msg): what up defcon

Sig #1 (r, s): (0x5d66e837a35ddc34be6fb126a3ec37153ff4767ff63cbfbbb32c04a795680491, )

Sig #1 (msg): uh oh this isn’t good

Sig #2 (r, s): (0x5d66e837a35ddc34be6fb126a3ec37153ff4767ff63cbfbbb32c04a795680491, 0xd67006bc8b7375e236e11154d576eed0fc8539c3bba566f696e9a5340bb92bee)

The prompt explains what is wrong, so all we have to do is figure out how to solve for the private key. A quick search will provide various explanations of the problem and how to solve it. Wikipedia provides a good explanation of how ECDSA signatures are generated and documents the solution to nonce reuse. We’ll describe the math here using the same variable names as Wikipedia.

Given two signatures s and s’ of different messages digests z and z’ which used the same nonce, the first step is solving for the private key is solving for k.

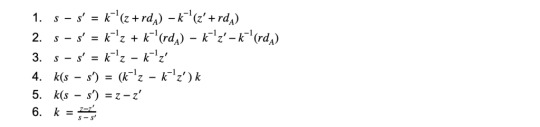
Now that we know k, we have enough public information to restructure the signature equation and solve for the private key d_a.

We can solve this problem in Python with the following code:

import hashlib

# secp256k1 order

order = int(“fffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141”, 16)

# Input from challenge

z = int(hashlib.sha256(“what up defcon”).hexdigest(), 16)

z_prime = int(hashlib.sha256(“uh oh this isn’t good”).hexdigest(), 16)

s = int(“1a53499a4aafb33d59ed9a4c5fcc92c5850dcb23d208de40a909357f6fa2c12c”, 16)

s_prime = int(“d67006bc8b7375e236e11154d576eed0fc8539c3bba566f696e9a5340bb92bee”, 16)

r = int(“5d66e837a35ddc34be6fb126a3ec37153ff4767ff63cbfbbb32c04a795680491”, 16)

# dividing within a field is not standard division so we need to define it as follows

def modinv(a, modulus): return pow(a, modulus — 2, modulus)

def divmod(a, b, modulus): return (a * modinv(b, modulus)) % modulus

# Solve for private key d

k = divmod(z — z_prime, s — s_prime, order)

d = divmod(k * s — z, r, order)

# output challenge flag

print(hex(d))

This correctly outputs the challenge flag 0x128e06938ac462d9.

Linkable Payments

By Max Mikhaylov

This is a cryptography challenge. We will use Python to solve it. I assume that you are familiar with scalar multiplication for elliptic curves over finite fields. If this topic doesn’t sound familiar, read the first 3 chapters of Jimmy Song’s Programming Bitcoin book. This is a prerequisite for understanding the challenge.

For this challenge I need only one nonstandard package — fastecdsa. We use it to do arithmetic on ECC points of brainpoolP160r1 curve. We will be using only two classes from that package: Point and brainpoolP160r1.

Examining the data

Looking at transactions that were broadcast to the node, we see that all of them contain an invalid destination key. The problem clearly establishes the format for ECC points and the destination key doesn’t follow it (‘dest_key’: ‘G0’). It’s not even a valid hex number.

But the transaction public key looks valid. Let’s try converting those public keys to ECC points on brainpoolP160r1 curve. Let’s write a function that converts a single public key to a point on the curve.

def key_to_point(key):

return Point(int(key[2:42], 16), int(key[42:], 16), curve=brainpoolP160r1)

If we try converting some public keys to points with this function, we will get an error: ValueError: coordinates are not on curve <brainpoolP160r1>

It looks like the public key provided by the sender is not on the brainpoolP160r1 curve. In fact, none of the provided public keys are on that curve. From the description of the transaction model from the Cryptonote whitepaper we know that the node needs to perform scalar multiplication using the sender’s transaction public key and its own private key. Is it dangerous for the node to perform this multiplication with a point that is not on the expected curve? Yes! We will find out why in a bit.

If the node’s implementation wasn’t flawed, it would have checked if the public key provided by the sender is on the expected curve and throw an exception if it is not on the curve (just like fastecdsa library does). However, the node accepted this public key, performed scalar multiplication using its private tracking key and tried to compare whether its version of the shared secret (P_prime) is different from the one provided by the sender (P). Only when comparing those values, the node threw an error since one of the values is not a valid ECC point (the destination key provided by the sender). To make matters worse (or better for us as an attacker), the node exposed its version of the shared secret (P_prime) in the log.

Analyzing ECC points

The first hint of the challenge tells us that we need to concentrate on these invalid ECC points provided by the sender. Since the flawed node software doesn’t check if the provided point is on the curve, we can monkey patch the Point class of fastecdsa library to remove the following check:

def point_init_monkey_patch(self, x, y, curve):

self.x = x

self.y = y

self.curve = curve

Point.__init__ = point_init_monkey_patch

We can now try converting tx_pub_key to ECC point for all transactions one more time; no error:

Input:

pub_key_points = txs_to_pub_key_points(txs) # txs is dict of txs.json contents

We can also convert shared secret values from node logs to ECC points, now that we monkey patched the ECC library:

def err_log_to_shared_secret_points(err_log):

shared_secret_points = []

for entry in err_log:

msg = entry[‘err_msg’]

shared_secret = msg.split(‘P_prime=’)[1].split()[0]

shared_secret_point = key_to_point(shared_secret)

shared_secret_points.append(shared_secret_point)

return shared_secret_points

shared_secret_points = err_log_to_shared_secret_points(err_log) # err_log is dict of err_log.json contents

Let’s go back to public key points. The first public key point looks very suspicious. I am talking about the Y-coordinate being 0. Let’s try calculating the order of this point.

Input:

def point_order(p):

for x in range(2, brainpoolP160r1.p):

if x * p == p:

return x — 1

point_order(pub_key_points[0])

Output:

2

This is very low order! Turns out other public key points have low order as well. Does this give us some way to derive the private key used by the node to calculate shared secrets?

Invalid-curve attack

It turns out that these exact conditions allow us to carry out an invalid-curve attack. You can read more about what an invalid-curve attack is in “Guide to Elliptic Curve Cryptography” by Hankerson, Menezes and Vanstone on page 182. Also read a recent CVE-2019–9836 describing this attack in a practical setting (this was the second hint for this challenge).

The gist of the attack: if we can make the node compute shared secrets from low order points of relatively prime order, and can find results of these computations, we can recover the secret using the Chinese Remainder Theorem (CRT). To be more specific, we need the product of all low order points to be greater than the private key in order for the recovered key to be unique (thus, match the private key). If we calculate the product of the order of all points in `pub_key_points`, we can in fact see that this number doesn’t fit in 160 bits, thus has to be larger than the private key used with brainpoolP160r1 curve.

Input:

product = 1

for point in pub_key_points:

product *= point_order(point)

from math import log2

log2(product)

Output:

175.1126248794482 # the product occupies 176 bits in binary representation

First, we need to be able to use the CRT. There are many resources on how CRT works, so you can read those if you are curious about math behind it. For solving this problem, I copied the CRT implementation from Rosetta Code.

We are now ready to perform the attack! The main idea behind this is the following:

We know that multiplying a low order point by a very large scalar (the private key) will result in a point of the same low order (the shared secret).

We can calculate the smallest possible scalar that, when multiplied by the public key, will result in the same low order shared secret.

We can do that by simply trying all possible scalars that are smaller than the order of the public key.

By bruteforcing the smallest possible scalar that gives us the shared secret when multiplied by the public key, we can construct a system of simultaneous congruences in the exact format that is suitable for applying the CRT. Since the product of all relatively prime orders is greater than the private key we are looking for, the result of applying the CRT is unique.

Input:

v = [] # can think of values in this list as the minimum number of EC additions of E_hat to itself to get shared_secret

moduli = [] # prime moduli of the system

print(“Constructing a system of simultaneous congruences:”)

for P_hat, shared_secret in zip(pub_key_points, shared_secret_points):

order = point_order(P_hat)

# search for shared_secret mod o_prime; i.e. the min number of additions of E_hat to itself to get shared_secret

for x in range(1, brainpoolP160r1.p):

if x * P_hat == shared_secret: # found the min number of additions

print(f’e ≡ {x} mod {order}; ’, end=’’)

v.append(x) moduli.append(order) break

Output:

Constructing a system of simultaneous congruences:

e ≡ 1 mod 2; e ≡ 1 mod 11; e ≡ 7 mod 23; e ≡ 1 mod 5; e ≡ 34 mod 41; e ≡ 4 mod 7; e ≡ 273 mod 293; e ≡ 161 mod 691; e ≡ 93 mod 347; e ≡ 7 mod 17; e ≡ 162 mod 229; e ≡ 19 mod 53; e ≡ 7 mod 13; e ≡ 380 mod 977; e ≡ 83 mod 89; e ≡ 82 mod 109; e ≡ 4771 mod 9767; e ≡ 381213 mod 439511; e ≡ 758 mod 10009; e ≡ 14048 mod 26459; e ≡ 11 mod 37; e ≡ 196934 mod 949213;

Input:

e = chinese_remainder(moduli, v)

hex(e)

Output:

‘0xdec1a551f1edc014ba5edefc042019’

This private key hex looks unusual… This is definitely a flag!

P.S. If you are curious about how I found low order points in the first place, see my question on Cryptography Stack Exchange that I asked when working on this challenge.

Schnorrer Signature

By Jesse Posner

This challenge describes a defective signature scheme called Schnorrer signatures. This scheme is nearly identical to Schnorr signatures, however, it contains a critical flaw that allows Schnorrer signatures, unlike Schnorr signatures, to be easily forged. The goal of the challenge is to produce a valid Schnorrer signature for a given public key and message.

A Schnorrer signature, and its defect, are best understood by contrasting them with a Schnorr signature. A Schnorr signature applies the Fiat-Shamir heuristic to the Schnorr identification protocol, an interactive proof-of-knowledge sigma protocol, and transforms it into a digital signature protocol.

In Schnorr, the Fiat-Shamir heuristic challenge is generated by hashing the message and the public nonce, but in Schnorrer the challenge is the hash of the message and the public key. By replacing the public nonce with the public key in the challenge hash, the Schnorrer signature undermines the security of the scheme.

Schnorr Identification Protocol

The Schnorr identification protocol consists of 3 elements: (1) a key generation algorithm, (2) a prover and (3) a verifier. The prover generates a secret, `x`, and wants to prove to the verifier that she knows `x` without revealing it to the verifier.

Both parties will need to agree on some parameters: a cyclic group, with a generator, `G`, and a prime modulus, `q`. For example, the Bitcoin protocol uses the secp256k1 parameters, with a generator specified by an elliptic curve point with compressed coordinates:

02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798

An uppercase letter, such as `G`, `P`, or `R`, denotes a group element, for example, an elliptic curve point. Lowercase letters denote scalar values, such as `x`, `r`, and `s`.

Key Generation Algorithm

The prover uses the key generation algorithm to produce a public-private key pair, `x` and `P`. `x` is an integer selected at random from a finite field with modulo `q`. The public key `P` is calculated by using `x` as a scalar value and multiplying it by `G`:

```x*G```

The private key, `x`, is the discrete logarithm of `P` with the base `G`, and thus the verifier is unable to efficiently derive the private key from the public key, and so the prover can reveal a public key without revealing the private key, hence the “public” and “private” denotations.

Protocol

Let’s suppose that Alice wants to prove to Bob that she knows the value `x`. Alice begins the Schnorr identification protocol by generating a nonce, `r`, to be used as a scalar, similar to the private key. However, unlike the private key, the nonce must be used just once (“for the nonce”). Alice then computes the value `r*G` to derive the group element `R`, similarly to how the public key was generated. This value, `R`, is typically referred to as the public nonce, or the nonce commitment. Once Alice has her public key, `P`, and public nonce, `R`, she sends those values to Bob.

Bob now must generate another scalar value called the challenge value, `c`. After Bob receives `P` and `R`, he then generates `c` and sends it to Alice. Note that while `c` is independent from `R`, it is very important that Bob wait until he has received `R` from Alice before sending `c` to her. In fact, if Bob fails to do this, and sends `c` to Alice prior to receiving `R`, Alice can trick Bob into believing that she has knowledge of the secret key without actually knowing it. The integrity of the verification depends on `R` being generated prior to `c`, as we will see shortly.

Alice completes the conversation with Bob by multiplying her private key, `x`, by the challenge, `c`, and adding that product to her private nonce, `r`, to produce what is referred to as the `s` value. `s` must be modulo `q` (all scalar values must be modulo `q` so that they fall within the curve order).

We can now see the purpose of the nonce: it allows Alice to produce a value that is the product of (1) the private key, `x`, and (2) a value chosen solely by Bob, namely, the challenge, `c`. Yet Alice must accomplish this without directly disclosing `x` to Bob. If we omitted the nonce from the protocol, then `s` would be equal to `x*c`, and, while this value would indeed prove Alice’s knowledge of `x` to Bob, it does so far too aggressively and allows Bob to trivially compute `x` by dividing `s` by `c`.

```x = s/c```

However, with the addition of the nonce, x is hidden from Bob and cannot be computed solely from `s`.

```x = (s — r)/c```

Upon receiving `s` from Alice, Bob verifies the outputs of the protocol, `s` and `R` as follows: Bob computes `s*G`, and checks whether that value is equal to the sum of (1) the public nonce, `R`, and (2) the public key, `P`, multiplied by the challenge, `c`. Bob can be confident that Alice knows `x` if this equality holds, because Bob scaled `P` by `c`, and yet Alice knew the discrete logarithm of the result (offset by the public nonce), `s`. Thus, unless Alice has an efficient means of calculating discrete logarithms, she must know `x`.

However, as alluded to above, if Bob provides `c` to Alice prior to receiving `R`, then Alice can choose a malicious `R` and trick Bob into verifying the output, despite Alice not actually having knowledge of the private key, `x`, and the nonce, `r`. Alice does this by selecting a random integer modulo `q` to be used as `s`, and then computes `s*G` and `c*P`. Next, Alice subtracts `c*P` from `s*G` to compute `R`.

```R := s*G — c*P```

Now Alice has a valid public nonce, `R`, without knowing the private nonce, `r`, and a valid `s` without knowing the private key, `x`. Thus, we can see that it is critically important that Bob not disclose `c` to Alice until he has received `R` from her, otherwise Alice can choose `R` maliciously, by computing the difference between `c*P` and `s*G`.

Schnorr Signature

The Fiat-Shamir heuristic is a method that transforms Sigma protocols into digital signature schemes. It does this by replacing the challenge value, `c`, with a cryptographic hash of (1) a message, `m`, which is the data that is being signed, and (2) the public nonce, `R`. Requiring `R` as an input to a hash function that creates `c` prevents Alice from computing `R` from `c*P` and `s*G`, because `c` is now generated based on `R`, and thus `R` must preexist `c`.

The signature protocol proceeds similarly to the identity protocol: Alice multiplies her private key, `x`, by the challenge value, `c`, and then adds it to the private nonce, `r`, to produce `s`. The signature consists of the pair of values, `s`, and the nonce commitment, `R`, which are provided to Bob by Alice. Bob can compute `c` himself because `c := H(m || R)`.

The structure of the verification algorithm is the same as the identity protocol: `s*G == R + c*P`

Schnorrer Signature

A Schnorrer signature is identical to a Schnorr signature, except the challenge value, `c`, is a hash of (1) the message and (2) the public key, `P`, instead of (1) the message and (2) the nonce commitment, `R`. This seemingly small modification to the scheme renders it insecure.

The forgery attack proceeds along the same lines as the identification attack described above. In the identification attack, Bob provided the challenge value to Alice prior to receiving the public nonce, `R`. Similarly, because the Schnorrer signature challenge value does not include `R`, Alice can reverse the order of the protocol, and choose an `s` value first, and then calculate `R` as the difference between `s*G` and `c*P`, and thus forge a signature, in other words, with this defect, Alice can produce a valid Schnorrer signature without knowing the private key, `x`, (and also without knowing the nonce, `r`).

Forging A Signature

By Jake Craige

This challenge is described as follows:

Given two Pedersen commitments in and out, you must construct a proof that the difference between the commitment amounts is zero. We’ll use the secp256k1 curve and define `g` as the standard base point of the curve and `h=g^SHA256(“CoinbaesRulez”)`.

We’ll define out input and output commitments as `in=g¹³³⁷⋅h⁹⁸⁷⁶` and `out=g²⁶⁷⁴ ⋅h³⁴⁵⁶` and walk through the evaluation here.

= in⋅out^−1

= (g¹³³⁷⋅h⁹⁸⁷⁶)⋅(g^−2674⋅h³⁴⁵⁶)^−1

= g^(1337+2674)⋅h^(9876−3456)

y = g⁴⁰¹¹⋅h⁶⁴²⁰

We see that this is not a commitment to zero and actually creates more money thaen went into it. Your task is to provide us a `(t, s)` pair that convinces a verifier that `y` is a commitment to zero even though that’s not true.

Here is the input data you should use to create the signature. The elliptic curve points (commitments) are provided in the SEC compressed encoding. For the signature, we’ll use the Schnorr Identification Protocol proof described in the attached PDF. You must use the provided nonce so that we get a deterministic outcome for the CTF verification.

in=0x25b0d4d0ad70054b53c16d6b3269b03e7b8582aa091317cab4d755508062c6f43

out=0x35e3bdfa735f413f2213aa61ae4f7622596feddb96ecc0f263892cb35ca460182

y=0x20ab37bbcc43b8e96714aae06fdc1bbfc386d0165afb69500c9df1553e6c94ed1

nonce=0x19

The submission should be in the format `(t, s)` where both `t` is the hex encoded compressed point and `s` is a hex encoded unsigned integer. They should both have a `0x` prefix and the parenthesis and `,` must be present to verify. An example format would be: `(0xdead, 0xbeef)`.

The problem with the construction defined above is how `h` is selected. For a pedersen commitment to be trusted no one can know the discrete log of `h` with respect to `g`. Restated: no one should know `x` such that `h=g^x`. Knowledge of that allows one to forge commitments.

Recall that our commitment looks like `y=g^a⋅h^b` where `a` is the amount and `b` is the blinding factor. We provide a proof for `y=h^z`. With a non-malicious prover, this proves a commitment to a zero amount because `y=g⁰⋅h^b=h^b`, so we simply prove that we know the blinding factor `b` and verify against the public key `y`.

Unfortunately, by naively deriving `h` from `g`, we know the discrete log and can forge the signature. Here’s how.

We first set up the equality we wish to forge, and restructure it such that everything is done in base `g`. This is the step that can only be done if you know the discrete log of `h` which is the value `x`.

From this, we can solve for the value `z` which is what we need to create the proof. For simpler notation, we drop the base to show how this value is solved for.

With that equation in hand, we can proceed to create the proof. The values for `a, b, x` can be found in the problem statement: `a=4011`, `b=6420`, and `x=SHA256(“CoinbaesRulez”)` We treat the byte output of the SHA256 function as big-endian to represent it as a number.

Using this information we can compute `z` using our equation from before. In Python this can be done as follows:

import hashlib

# secp256k1 order

order = int(“fffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141”, 16)

def modinv(a, modulus): return pow(a, modulus — 2, modulus)

a = 4011

b = 6420

x = int(hashlib.sha256(“CoinbaesRulez”).hexdigest(), 16)

z = (a * modinv(x, order) + b) % order

Now that we know `z`, the last step is to create a proof of knowledge of discrete log to submit as the solution flag. This is done using the Schnorr Identification Protocol where we use the Fiat-Shamir transform to make it non-interactive by setting the challenge value to be the big-endian representation of the SHA256 output of the compressed points H, T, and Y concatenated together as bytes. The problem description provides a fixed nonce to make the output deterministic. The solution in Python, building on the former Python code, is:

from fastecdsa.curve import secp256k1

from fastecdsa.point import Point

from fastecdsa.encoding.sec1 import SEC1Encoder

# Challenge input

H = secp256k1.G * x

r = 0x19

# Generate the proof of knowledge of discrete log

T = H * r

Y = H * z

hashInput = SEC1Encoder.encode_public_key(H)

hashInput += SEC1Encoder.encode_public_key(T)

hashInput += SEC1Encoder.encode_public_key(Y)

c = int(hashlib.sha256(hashInput).hexdigest(), 16)

s = (r + c*z) % order

# Print the formatted flag

print(“(0x” + SEC1Encoder.encode_public_key(T).encode(“hex”) + “, 0x” + format(s, ‘x’) + “)”)

To see more about how these Pedersen Commitments are used in practice in blockchains, I recommend reading up on MimbleWimble based blockchains.

Conclusion

This concludes our writeups for the Capture the Coin competition. We hope you enjoyed learning more about a variety of blockchain security topics and can join us again next year.

In the meantime, if solving blockchain security challenges is something that you see yourself doing full time, then join us at Coinbase to help build the most trusted brand in the Crypto here.

This website contains links to third-party websites or other content for information purposes only (“Third-Party Sites”). The Third-Party Sites are not under the control of Coinbase, Inc., and its affiliates (“Coinbase”), and Coinbase is not responsible for the content of any Third-Party Site, including without limitation any link contained in a Third-Party Site, or any changes or updates to a Third-Party Site. Coinbase is not responsible for webcasting or any other form of transmission received from any Third-Party Site. Coinbase is providing these links to you only as a convenience, and the inclusion of any link does not imply endorsement, approval or recommendation by Coinbase of the site or any association with its operators.

All images provided herein are by Coinbase.

Capture the Coin — Cryptography Category Solutions was originally published in The Coinbase Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.

from Money 101 https://blog.coinbase.com/capture-the-coin-cryptography-category-solutions-fe94d82165c5?source=rss----c114225aeaf7---4 via http://www.rssmix.com/

[mathematicianadda]

Generic behavior amongst "polynomialish" models of $\mathsf{Q}$ https://ift.tt/eA8V8J

For $\mathcal{R}=(R_i)_{i\in\mathbb{N}}$ a sequence of countable commutative ordered rings such that $R_i$ is an sub-ordered ring of $R_{i+1}$ and $R_0=\mathbb{Z}$, let $$Poly_\mathcal{R}=\{\sum_{i<n}a_ix^i\in (\bigcup_{i\in\omega}R_i)[x]: a_i\in R_i\}$$ be the set of polynomials whose $i$th term comes from the $i$th ring in the sequence. $Poly_\mathcal{R}$ naturally inherits the structure of an ordered ring, namely by taking as the set of positive elements all those $p$ whose leading coefficient is positive in the sense of the appropriate $R_i$. For example, we'll have $x>1$ since the leading coefficient of $x-1$ is $1$ which is positive.

The set $Poly_\mathcal{R}^+$ of nonnegative elements of $Poly_\mathcal{R}$ is a nonstandard model of Robinson's $\mathsf{Q}$. Unsurprisingly the theory of $Poly^+_\mathcal{R}$ depends on $\mathcal{R}$. I'm interested in the "generic" behavior of such models.

To make this precise, let $\mathfrak{X}$ be the space of all such ordered ring sequences topologized by taking as basic open sets of those of the form $$[(R_i)_{i<n}]:=\{\mathcal{S}=(S_i)_{i\in\omega}: \forall i<n(S_i=R_i)\}$$ for each finite sequence of ordered rings $(R_i)_{i<n}$. (Fine, this $\mathfrak{X}$ is a proper-class-sized space; do any of the usual tricks to fix this.) Say that a sentence $\varphi$ in the language of Robinson arithmetic is generically true (resp. false) iff $\{\mathcal{R}: Poly_\mathcal{R}^+\models\varphi\}$ is comeager in $\mathfrak{X}$ (resp. meager).

For example, "Every number is either even or odd" is neither generically true nor generically false. On the other hand, the more complicated sentence

$(*)\quad$ "There is some $k$ such that for all $n>k$ there is some $m<k$ such that $n+m$ is even"

is generically true. Given a (code for a) basic open set $(R_i)_{i<n}$, consider the extension $(S_i)_{i<n+1}$ with $S_i=R_i$ for $i<n$ and $S_n$ be some ring containing $R_{n-1}$ as a subring in which $2x=1$ has a solution. Then every $\mathcal{R}\in[(S_i)_{i<n+1}]$ has $Poly_\mathcal{R}^+\models(*)$: just take $k=x^n$. (Note that this is nontrivial since $Poly_{(\mathbb{Z},\mathbb{Z},\mathbb{Z}, ...)}^+\models\neg(*)$.)

In general, many basic facts about modular arithmetic have "perturbed" versions a la $(*)$ above which are generically true. I'm interested in unpacking this more. Suppose $\varphi$ is a sentence of the form $\forall x_1,...,x_n\exists y_1,...,y_k\theta(x_1,...,x_n,y_1,...,y_k)$ with $\theta$ quantifier-free such that $x_i$ occurs in $\theta$ exactly $m_i$-many times. Define the perturbed version of $\varphi$, which I'll denote by "$\varphi^\circ$," as: $$\exists u\forall x_1,...,x_n\exists x'_{1, 1}, x'_{1,2}, x'_{1,3},..., x'_{1, m_1}, ..., x'_{n, 1}, ..., x'_{n, m_n}\mbox{ such that }$$ $$\bigwedge_{i\le n, j\le m_i}\lfloor{x_i\over u}\rfloor\le x'_{i,j}\le x_iu\quad\mbox{ and }$$ $$\quad\exists y_1,...,y_k(\theta(\langle x'_{1,1},...,x'_{1,m_1}\rangle, ..., \langle x'_{n,1},..., x'_{n,m_n}\rangle, y_1,...,y_k))$$ where "$\theta(\langle x'_{1,1},...,x'_{1,m_1}\rangle, ..., \langle x'_{n,1},..., x'_{n,m_n}\rangle, y_1,...,y_k)$" is the formula gotten from $\theta(x_1,...,x_n,y_1,...,y_k)$ by replacing the $j$th instance of $x_i$ with $x'_{i,j}$.

The idea is that $\varphi^\circ$ doesn't require $\exists\overline{y}\theta$ to hold on every tuple of $x$s; we're allowed to perturb the inputs by up to a fixed factor $u$. The replacement of the single variable $x_i$ with the several variables $x'_{i,1},...,x'_{i,m_i}$ guarantees that "$\varphi^\circ\wedge\psi^\circ=(\varphi\wedge\psi)^\circ$" in the appropriate sense.

My question is:

Suppose $\varphi$ is an $\forall\exists$-sentence in the language of Robinson arithmetic and $\mathbb{N}\models\varphi$. Is $\varphi^\circ$ generically true?

(We can also consider "perturbed versions" of higher-complexity sentences, but the $\forall\exists$-case seems already interesting.)

from Hot Weekly Questions - Mathematics Stack Exchange Noah Schweber from Blogger https://ift.tt/3fm8SuQ

[mygreentech-blog]

New AWS cloud services

Here, Amazon has driven the way. Saying this doesn't imply that there isn't rivalry. Microsoft, Google, IBM, Rackspace, and Joyent are for the most part producing splendid arrangements and cunning programming bundles for the cloud, however no organization has accomplished more to make highlight rich packs of administrations for the cloud than Amazon. Presently Amazon Web Services is zooming ahead with a gathering of new items that blow separated the possibility of the cloud as a clear slate. With the most recent round of devices for AWS, the cloud is that significantly closer to turning into an attendant sitting tight for you to wave your hand and give it straightforward guidelines. 

Glue.

Paste is another accumulation of Python contents that consequently slithers your information sources to gather information, apply any vital changes, and stick it in Amazon's cloud. It ventures into your information sources, catching information utilizing all the standard acronyms, as JSON, CSV, and JDBC. When it snatches the information, it can investigate the construction and make proposals.

The Python layer is interesting because you can use it without writing or understanding Python—although it certainly helps if you want to customize what’s going on. Glue will run these jobs as needed to keep all the data flowing. It won’t think for you, but it will juggle many of the details, leaving you to think about the big picture.

FPGA.

Field Programmable Gate Arrays have for quite some time been a mystery weapon of equipment fashioners. Any individual who needs an uncommon chip can fabricate one out of programming. There's no compelling reason to fabricate custom veils or fuss over fitting every one of the transistors into the littlest measure of silicon. A FPGA takes your product depiction of how the transistors should function and revamps itself to act like a genuine chip.

Amazon's new AWS EC2 F1 conveys the intensity of FGPA to the cloud. In the event that you have exceptionally organized and tedious figuring to do, an EC2 F1 case is for you. With EC2 F1, you can make a product portrayal of a speculative chip and order it down to a modest number of doors that will process the appropriate response in the briefest measure of time. The main thing quicker is carving the transistors in genuine silicon. Learn AWS training in Chennai at Greens Technologys.

Who may require this? Bitcoin excavators figure the equivalent cryptographically secure hash work a bazillion times every day, which is the reason numerous bitcoin mine workers utilize FPGAs to accelerate the inquiry. Anybody with a comparable minimized, dreary calculation you can compose into silicon, the FPGA example gives you a chance to lease machines to do it now. The greatest champs are the individuals who need to run computations that don't delineate onto standard guidance sets—for instance, when you're managing bit-level capacities and other nonstandard, non arithmetic estimations. In case you're essentially including a section of numbers, the standard occurrences are better for you. In any case, for a few, EC2 with FGPA may be a major win.

Blox.

As Docker eats its way into the stack, Amazon is attempting to make it less demanding for anybody to run Docker examples anyplace, whenever. Blox is intended to juggle the groups of occurrences with the goal that the ideal number are running—no more, no less. 

Blox is occasion driven, so it's somewhat less complex to compose the rationale. You don't have to continually survey the machines to perceive what they're running. They all report back, so the correct number can run. Blox is additionally open source, which makes it simpler to reuse Blox outside of the Amazon cloud, on the off chance that you should need to do as such.

X-Ray

Observing the effectiveness and heap of your cases used to be just another employment. On the off chance that you needed your bunch to work easily, you needed to compose the code to track everything. Numerous individuals got outsiders with great suites of apparatuses. Presently Amazon's X-Ray is putting forth to do a great part of the work for you. It's contending with some outsider devices for watching your stack. 

At the point when a site gets a demand for information, X-Ray follows as it as streams your system of machines and administrations. At that point X-Ray will total the information from various occasions, districts, and zones with the goal that you can stop in one place to signal a headstrong server or a wedged database. You can watch your tremendous realm with just a single page.

Rekognition.

The calculations are vigorously tuned for facial acknowledgment. The calculations will signal faces, at that point contrast them with one another and references pictures to enable you to recognize them. Your application can store the meta data about the appearances for later handling. When you put a name to the metadata, your application will discover individuals wherever they show up. Distinguishing proof is just the start. Is it accurate to say that someone is grinning? Are their eyes shut? The administration will convey the appropriate response, so you don't have to get your fingers messy with pixels. On the off chance that you need to utilize great machine vision, Amazon will charge you not by the snap but rather by the look at each picture.

AWS training @ Greens Technologys.

If you are seeking to get a good AWS training in Chennai, then Greens Technologys should be the first and the foremost option.

—We are named as the best training institute in Chennai for providing the IT related trainings. Greens Technologys is already having an eminent name in Chennai for providing the best software courses training.

—We have more than 115 courses for you. We offer both online and physical trainings along with the flexible timings so as to ease the things for you.  

[tilde-he]

“finite“ field field extensions with characteristic a nonstandard prime, and the inverse Galois problem

So, the inverse Galois problem: Given a (finite) group, is it the Galois group of some field extension? Or, rather, is there, for every finite group, some field extension which has that as its Galois group?

To quote Wikipedia : “ This problem, first posed in the early 19th century,is unsolved. “

Here is some reasoning that I think makes sense. It does not solve the problem (duh. This is a blog post, not a paper.) but I think it is interesting in relation to the problem.

If G is some group, and if it cannot be proven in (1st order?) Peano arithmetic that G is not the Galois group of any field extension of finite fields, or just of fields of nonzero characteristic (assuming that this statement can be expressed in Peano arithmetic in an appropriate way), then, by the model existence theorem, there is a model of arithmetic in which there is such a field extension.

Now, I don’t exactly “know” model theory, so this next thing I say could be quite wrong, but my impression is that we can have a nonstandard model of set theory where the set whose existence is guaranteed by the axiom of infinity (i.e. our set of natural numbers), is actually the set of elements for the nonstandard model of peano arithmetic that we took.

And, this nonstandard model of set theory is living inside our normal set theory, and its sets are like, also actual sets, and the “is an element of” is the actual “is an element of” of our actual set theory. I think this is called an inner model (however, I’m not sure. Wikipedia seems to say that for it to be an inner model, it has to have all of its ordinals in common? which doesn’t seem to be what is the case in what I’m describing, so maybe it doesn’t count as an inner model.).

Anyway, so, we have our nonstandard model of set theory and of the natural numbers, and in this nonstandard model we have that there is a nonstandard prime p such that there is a field F of characteristic p, and a field extending it, K, such that the field extension K/F is Galois.

Now, if we look at one of these fields in this nonstandard model of set theory, from the perspective of our actual set theory, while it won’t be a field of finite characteristic, it should still be a field, just of characteristic 0 instead. Because, the function for the multiplication, addition, negation, etc. will still all be valid functions from the perspective of the actual set theory, so the field axioms should still be satisfied. (characteristic 0 because there is no natural number n such that 1 + 1 + 1 + ... n times, = 0 ).

And, furthermore, the field extension should still be a field extension, and each of the field automorphisms from before should still be field automorphisms.

However, I think that, when looking at the field extension this way, there may be intermediate fields that aren’t there in the nonstandard model, because, essentially, the power sets don’t actually have to have all the subsets, only the ones that can be like, specified, or whatever.

Similarly, there may be additional automorphisms that don’t exist in the nonstandard model, but do “in reality”.

And, perhaps in our actual set theory, K/F isn’t even a Galois extension!

But, this is no issue!

The automorphisms that we had, that inside the nonstandard model comprised Gal(K/F) , all still work as automorphisms, in our actual set theory, and still form a group, just not necessarily Gal(K/F).

So, if we just take K/(the fixed field of that group) , we will then get a Galois extension, which has as its Galois group, that same group, which is isomorphic to G.

So, if my understanding of model theory isn’t too broken, then: If it can’t be proven that there is no prime p such that G is (isomorphic to) the Galois group of some field extension with characteristic p, then there is a Galois field extension of characteristic 0, the Galois group of which is (isomorphic to) G .

So, the possible “answers” to the inverse Galois problem for a finite group G are: 1) “Yes, there is such a field extension” 2) “No, it can be proven that no field extension produces that group as its Galois group.” 3) “No, and it can be proven that no field extension of positive characteristic produces such a Galois group, but while there is also no such one for characteristic 0, this cannot be proven.”

Actually, come to think of it, if it couldn’t be proven about the characteristic 0 case, then wouldn’t there also be a nonstandard model of, something, where there was one with char 0? Could one then extract that to get an actual one of char 0 as well? I suspect the answer is yet.

So, in that case, I think that this seems to kinda point at a way to show that: If a finite group G is not the Galois group of any field extension, then this fact can be proven about G.

So, that’s nice.

There’s, ... probably a way to prove that without resorting to talking about nonstandard models. This is probably way overkill to show something that people presumably already knew. (Or just wrong, but it seems right to me.)

[mathematicianadda]

Is there a natural intermediate version of PA?

Below, "logic" means "regular logic containing first-order logic" in the sense of Ebbinghaus/Flum/Thomas.

Setup

For a logic $\mathcal{L}$, let $\mathcal{PA}(\mathcal{L})$ be the set of $\mathcal{L}$-sentences in the language of arithmetic consisting of:

the ordered semiring axioms, and

for each $\mathcal{L}$-formula $\varphi(x,y_1,...,y_n)$ the induction instance $$\forall y_1,...,y_n[[\varphi(0,y_1,...,y_n)\wedge\forall x(\varphi(x,y_1,...,y_n)\rightarrow\varphi(x+1,y_1,...,y_n))]\rightarrow\forall x\varphi(x,y_1,...,y_n)].$$

(Note that even if the new logic $\mathcal{L}$ has additional types of variable - e.g. "set" variables - the corresponding induction instances will only allow "number" variables $y_1,...,y_n$ for the parameters.)

For example, $\mathcal{PA}(FOL)$ is just the usual (first-order) PA, and $\mathcal{PA}(SOL)$ characterizes the standard model $\mathbb{N}$ up to isomorphism. Also, we always have $\mathbb{N}\models_\mathcal{L}\mathcal{PA}(\mathcal{L})$.

Note that it's not quite true that $\mathcal{PA}(SOL)$ "is" second-order PA as usually phrased - induction-wise, we still have a scheme as opposed to a single sentence. However, induction applied to "has finitely many predecessors" gets the job done. (If we run the analogous construction with ZFC in place of PA, though, things seem more interesting ....)

Question

Say that a logic $\mathcal{L}$ is PA-intermediate if we have $PA<\mathcal{PA}(\mathcal{L})<Th_{FOL}(\mathbb{N})$ in the following sense:

There is a first-order sentence $\varphi$ such that $PA\not\models\varphi$ but $\mathcal{PA}(\mathcal{L})\models\varphi$.

There is a first-order sentence $\theta$ such that $\mathbb{N}\models\theta$ but $\mathcal{PA}(\mathcal{L})\not\models\theta$.

Is there a "natural" PA-intermediate logic?

(This is obviously fuzzy; for precision, I'll interpret "natural" as "has appeared in at least two different papers whose respective authorsets are incomparable.")

Partial progress

A couple non-examples:

Infinitary logic $\mathcal{L}_{\omega_1,\omega}$ is not PA-intermediate, since in fact $\mathcal{PA}(\mathcal{L}_{\omega_1,\omega})$ pins down $\mathbb{N}$ up to isomorphism (consider $\forall x(\bigvee_{i\in\omega}x=1+...+1\mbox{ ($i$ times)}$). So both second-order and infinitary logic bring in too much extra power.

Adding an equicardinality quantifier ($Ix(\varphi(x);\psi(x))$ = "As many $x$ satisfy $\varphi$ as $\psi$") also results in pinning down $\mathbb{N}$ up to isomorphism (consider "$\neg$ As many $x$ are $<k$ as are $<k+1$"). If we add the weak equicardinality quantifer $Qx\varphi(x) = Ix(\varphi(x);\neg\varphi(x))$, on the other hand, we wind up with a conservative extension of $PA$. That said, the latter is stronger semantically: no countable nonstandard model of $PA$ satisfies $\mathcal{PA}(FOL[Q])$ (to prove conservativity over $PA$ we look at the $\omega_1$-like models).

The proof of Lindstrom's theorem yields a weak negative result: if $\mathcal{L}$ is a logic strictly stronger than first-order logic with the downward Lowenheim-Skolem property, then we can whip up an $\mathcal{L}$-sentence $\varphi$ and an appropriate tuple of formulas $\Theta$ such that $\varphi$ is satisfiable and $\Theta^M\cong\mathbb{N}$ in every $M\models\varphi$. So an example for the above question would have to either allow nasty implicit definability shenanigans or lack the downward Lowenheim-Skolem property. This rules out a whole additional slew of candidates. That said, there is a surprising amount of variety among logics without the downward Lowenheim-Skolem property even in relatively concrete contexts - e.g. there is a compact logic strictly stronger than FOL on countable structures.

from Hot Weekly Questions - Mathematics Stack Exchange from Blogger https://ift.tt/3alb3wM