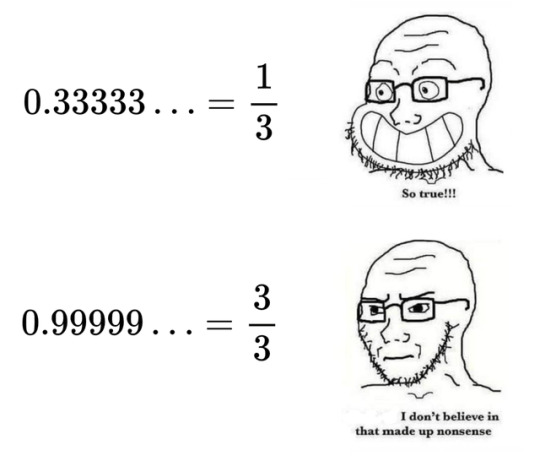
#mathpost
Explore tagged Tumblr posts
Text

Hi
I haven't produced any quality artposting or mathposting lately. Instead I made a chud wojak on desmos.
I made him out of cone sections and linear functions (I guess some people consider them degenerate conics) + one (1) 3rd degree polynomial.
He's upset because he's all rainbow-y and he thinks that's gay.
#mathpost#mathblr#graphing calculator art#desmos art#this thing is actually like a few months old now but I forgot to post it#math#wojak
11 notes
·
View notes
Text
The phrase "give a single fuck" implies fucks form part of a group with a multiplicative identity. However, they are not commutative because giving a fuck before an event has a different effect than giving a fuck afterwards. This also implies that there is a multiplicative inverse to giving a fuck, which in general can be shown to be true.
Thus, fucks can form a non-commutative multiplicative group.
#mathpost#mathblr#group theory#maths posting#I dont know anything about group thoery and made all of this up
165 notes
·
View notes
Note
Hello! Hope you don’t mind receiving an out-of-the-blue ask, but I’ve enjoyed many of your math posts and am wondering if you have an opinion on the book I just started, “The Skeleton Key of Mathematics” by D. E. Littlewood. It seems to be an attempt to explain quite advanced algebra in terms accessible to the non-specialist. I enjoyed math in school but am now in the humanities, so I suspect I am in its target audience! But by the same token I can’t judge whether it’s accurate/reliable…. :-)
I'm not familiar with this book, but will post this ask publicly and see if anyone following me has opinions.
9 notes
·
View notes
Text
rb this with your favorite math concepts/books/videos... things u enjoy and that make you excited! (or reply but i want to hear about it and if you rb it then i hear more cool stuff from more people)
my favorite books are the grapes of math and things to make and do in the fourth dimension. i'm also reallyyyy wanting to read number freak and godel, escher, bach. concepts i love are chaos theory, non-euclidean geometry, and dimensions beyond 3rd!
#math#mathblr#mathematics#pi#calculus#algebra#geometry#topology#pure math#mathcore#mathpost#mathematiques
61 notes
·
View notes
Text
Grids of Sensors in Non-Commutative Space
There's an idea of "non-commutative geometry" which seeks to view non-commutative algebras as if they were dual to some "non-commutative space" in the same way that commutative $C^*$-algebras (over the complex numbers) can be viewed as being the spaces of continuous complex valued functions on the locally compact Hausdorff space of that algebra's "spectrum" (or, specifically, the algebra of such functions that "vanish at infinity").
Some have considered this in the context of quantum mechanics, with the idea that, just as the operators for position along some axis and momentum along that axis, don't commute, perhaps the same is true for position along one axis and position along a different (orthogonal) axis. (I think there is the idea that this might help prevent some singularities in quantum gravity or something? idk. There's some kind of motivation for it.
This idea seems rather counterintuitive to me. With position and momentum not commuting (and their commutator being a constant, rather than some operator that could be zero in some states), and therefore things not having a simultaneously well defined position and momentum, this isn't too too hard to accept. Being able to say "here's the wavefunction in the position basis" and "here's the wavefunction in the momentum basis", seems nice enough. But, for position in one axis and in another axis to be not simultaneously well definable, seems harder to imagine. Like, if there was a maximum that the product of uncertainty in position and in momentum, could be.
The idea comes to mind of those simulations of "how it would look if you were walking around some city, if the speed of light was super slow". And then the question becomes, "if the degree of non-commutativity between different axiis was non-negligible, what would it look like?"
If one wants to consider the algebra for a quantum mechanical system with two non-commutative dimensions of space, one option is to consider the unital C^* algebra generated by self-adjoint operators q_x, q_y, p_x, p_y , subject to the relations: [q_x,p_x] = i hbar , [q_y, p_y] = i hbar , [q_x, p_y] = 0, [q_y, p_x] = 0 , [q_x, q_y] = i theta .
If one then takes the Hamiltonian for a 2D quantum simple harmonic oscillator, but using these q_x and q_y, and p_x and p_y , in place of the usual position and momentum operators, one can still do things like finding the spectrum of the Hamiltonian, etc. It turns out that one can even define some modified operators Q_x, Q_y, P_x, P_y in terms of our q_x, q_y, p_x, p_y , such that [Q_x, Q_y]=0 , P_x = p_x, P_y = p_y, and the Q_x, Q_y and the P_x, P_y have the same commutation relations with each-other as the normal position and momentum operators do. So, one can end up describing wavefunctions in the Q_x, Q_y basis or in the P_x, P_y basis, with Q_x and Q_y acting sorta like position, even though they aren't our actual position operators, and if we do this, then our simple harmonic oscillator defined in terms of q_x, q_y, p_x, p_y , ends up, when viewed in terms of Q_x, Q_y, P_x, P_y, being like a simple harmonic oscillator except with a term added for a magnetic field (proportional in strength to theta, and inversely proportional to hbar)
This is all stuff that I read about just recently. I'm not sure how it works in 3D. I imagine something similar, but the way of defining the Q_x and Q_y is probably substantially more complicated?
My idea (which others may have had before and investigated thoroughly, idk, I haven't done a literature search) is to, in order to think about "what things would look like in a world with non-commutative geometry (where the non-commutativity is large enough to be noticable at macroscopic scales) is to consider something like a "camera" made of a grid of detectors. Even though we don't really have a good notion of "points in space" in this kind of setting, we can still define an operator for "the distance between two particles" ( sqrt((q_{x,i} - q_{x,j})^2 + (q_{y,i} - q_{y,j})^2) ) and use this to write a Hamiltonian where there is a potential energy term which encourages each particle ("sensor") to be around some prescribed distance to each of its immediate neighbors, and then consider a ground state for this system. (Oh, q_{x,i} and q_{x,j} should commute with each-other btw. Operators for particle i and operators for particle j should commute with each-other. ) In order to say something to the effect of "our grid of sensors is located here in our lab, not moving", I think the grid should be labeled by pairs of integers between -N and N , and that the 4 corners should be "pinned" at certain coordinates (proportional to N) by replacing the position operators for those particles with just constants which should be coordinate for the particle in question. This is maybe somewhat unnatural because that would imply that at these corners the sensors there would have well defined coordinates in both x and y simultaneously (which would normally be impossible for particles in this non-commutative space), but we could just have those 4 particles not behave as sensors I guess. Anyway, if we take the limit as N goes to infinity, they would be far away from the origin, so hopefully this unnatural pinning wouldn't matter too much to things near the middle of the grid?
Then, if we want to ask about the location of some particle that isn't part of our grid of sensors, we can look at the projections for "is the distance between the particle and sensor j less than (some distance)?". Of course, these projections might not commute with each-other..? But, even if they don't, we can still use them for a Hamiltonian that represents particles being detected at whatever sensor they are nearby, and look at the probability distribution over "what detector was it detected at" that way, without needing to have "it is at detector i" and "it is at detector j" be commuting projections.
Oh, also, maybe should look at the limit where the masses of each the detectors are large (and equal to each-other), and/or where hbar is small, so that way the position vs momentum uncertainty doesn't play as large a role, just the uncertainty between x and y position?
If anyone has any thoughts on this, I'd like to hear it. (If you are aware of someone who has done this already, I'd especially like to hear it. I want answers, and I don't have time to work through stuff to find them, at least for now.)
#physics#mathpost#non-commutative geometry#quantum mechanics#math#I should be finishing writing dissertation not thinking about distractions like this!#mathblr
1 note
·
View note
Text
Talking about a YouTube video, I just said
"who's watching an hour long video on the mathematics of countdown? Not people who think 25 and 100 contain fundamentally different information."
0 notes
Text
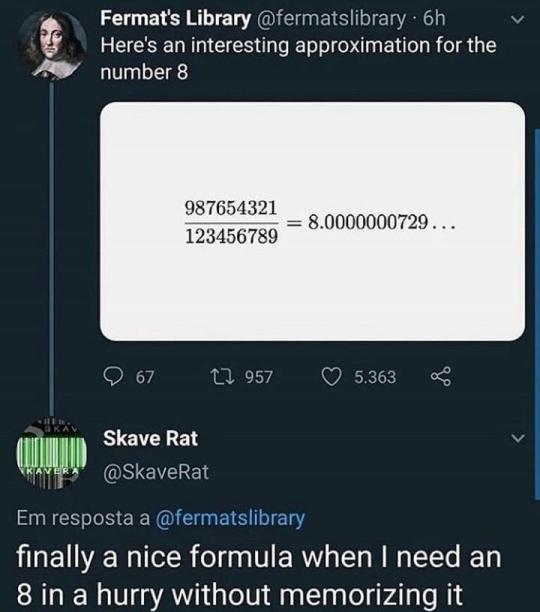
#rule#r/196#196#r196#apartmentofawesome#ruleposting#/r/196#/196#196 rule#19684#mathematics#mathblr#mathposting#math post#math
14K notes
·
View notes
Text
Also stop 🫨🫨I'm such a cringe loner 🤣🤣🤣pls send me asks 💀����or smth 🤷🤷I'll love I to the end of time 🤪🤪

#cats#eurovision#idk what im doing#farmer george#king george iii#mathpost#queen charlotte#queen charlotte: a bridgerton story#shit post#spam blogs#brimsley#gaming#idk what else to hashtag#queen elizabeth’s 1968 land rover is up for sale at auction for eye watering price#jesus#jesusislord#jesus he knows me#jesusisthewaythetruthandthelife#trisha#trisha paytas#twilight#actually mentally ill#sadbeautifultragic#cringe#anyway lmao#harry styles#me irl#gay men#lana del gay#make it stop
1 note
·
View note
Text
i love it when mathematicians use the word "invoke" to basically mean "use". like yes i am a wizard (mathematician) invoking powerful chain lightning spells (using fermat's little theorem) to cut down all who stand in my way (get rid of annoying exponents)
6K notes
·
View notes
Text
the first rule of fight club is that two fight clubs are equal if they have the same members
1K notes
·
View notes
Photo
Thanks for writing this! Mentioning that the issue is the sign getting flipped intrigues me a bit. I like superalgebras. The candidate monoidal product failing to be associative due to a sign error reminds me of uh, supermonoidal categories? Where (A \otimes B) (C \otimes D) = (-1)^{|B| |C|} (A C) \otimes (B C) .
This wouldn’t happen to be anything like that, would it?
I guess not, as I guess what you described is more like, (A \otimes B) \otimes C = - A \otimes (B \otimes C) ?
But, still, I am led to wonder, “what if instead of trying to get rid of the sign issues, we embrace them somehow?” . Maybe that’s not a good idea here though.

the stable homotopy category by Cary Malkiewich
78 notes
·
View notes
Text
I really really REALLY wish that 0 divided by 1 was undefined, because irrespective of how much damage that would do to all of mathematics, the existence of an "antiprime", divisible by every number except 1 and itself, would be so funny
123 notes
·
View notes
Text
There should be a conlang community but for math. I wanna see counting with factorial base systems and people make up symbols for increasingly useless numbers. Maybe this can make some calculations more intuitive and others much more cursed.
844 notes
·
View notes